解析几何中的定点与定值问题

王建勋（山东省临沂第一中学）

解析几何中的定点与定值问题

王建勋
（山东省临沂第一中学）

曲线与方程是高中解析几何的重点知识，而其中的定点、定值问题则是高考的热点问题.综观全国各地的高考，此类问题多见于数学试题的压轴题，学生多感到吃力.为此，本文将结合高考实例给出此类题目的一般解题思路，供大家参考.

一、定点问题

定点问题常见解题思路：（1）假设定点坐标，根据题意选择参数，建立一个直线系或曲线系方程，而该方程与参数无关，故得到一个关于定点坐标的方程组，以这个方程组的解为坐标的点即所求定点.（2）从特殊位置入手，找出定点，再证明该点适合题意.（3）由直线方程确定定点，若得到了直线方程的点斜式：y－y0=k（x－x0），则直线必过定点（x0，y0）；若得到了直线方程的斜截式：y＝kx＋m，则直线必过定点（0，m）.

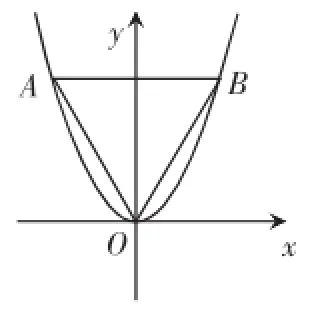
所以抛物线E的方程为x2=4y

即（y12+y1-2）+（1-y1）y0=0（*）

解得y1=1，故以PQ为直径的圆恒过y轴上的定点M（0，1）.

故若满足条件得点M存在，只能是M（0，1）.

以下证明点M（0，1）就是所要求的点.

故以PQ为直径的圆恒过y轴上的定点M.

二、定值问题

解析几何中的定值问题是指某些几何量（线段的长度、图形的面积、角的度数、直线的斜率等）的大小或某些代数表达式的值等和题目中的参数无关，不依参数的变化而变化，而始终是一个确定的值.基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关.常用的解决问题的方法有：（1）从特殊入手，求出定值，再证明这个值与变量无关.（2）直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.在这类试题中选择消元的方向是非常关键的.

例2.（2014年江西高考）如图，已知抛物线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）.

（1）证明：动点D在定直线上；

证明：（1）依题意可设A（x1，y1），B（x2，y2），并设直线AB的方程为y＝kx+2，代入x2=4y，得x2=4（kx+2），即x2-4kx-8=0，则有x1x2=-8，

因此动点D在定直线y=-2（x≠0）上.

（2）依题设，切线l的斜率存在且不等于0，设切线l的方程为y＝ax＋b（a≠0），代入x2=4y得x2=4（ax＋b），即x2-4ax-4b=0，由Δ=0得（4a）2+16b=0，化简整理得b=-a2.

故切线l的方程可写为y＝ax-a2.

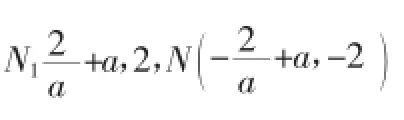
三、思考与练习

1.（2007年山东文）已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1．

（1）求椭圆C的标准方程；

（2）若直线l∶y=kx+m与椭圆C相交于A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点．求证：直线l过定点，并求出该定点的坐标．

（1）求椭圆C的方程；

（2）连接AE，BD，试探索当直线l的倾斜角变化时，直线AE与BD是否相交于定点？若是，请求出定点的坐标，并给予证明；否则，说明理由．

·编辑鲁翠红