基于非圆信号特征的实值张量ESPRIT算法

2016-09-07司伟建曲志昱米胜男

系统工程与电子技术 2016年9期

关键词：接收数据运算量张量

司伟建, 禹　芳, 曲志昱, 米胜男

(哈尔滨工程大学信息与通信工程学院, 黑龙江哈尔滨 150001)

基于非圆信号特征的实值张量ESPRIT算法

司伟建, 禹芳, 曲志昱, 米胜男

(哈尔滨工程大学信息与通信工程学院, 黑龙江哈尔滨 150001)

基于最大非圆率非圆信号特点,提出一种实值张量旋转不变子空间(estimationsignalparametersviarotationalinvariancetechniques,ESPRIT)算法。首先,通过研究张量与矩阵之间的转化关系,将阵列接收数据矩阵推广到张量空间;然后,利用欧拉公式将阵列接收数据张量转化成余弦与正弦数据张量,根据阵列维数将其分别在各维上加以拼接,并对拼接的实值数据张量做高阶奇异值分解,获取信号子空间;最后,通过构造选择矩阵和进行特征分解,来联合估计阵列各维相位差,实现波达方向估计。实验仿真结果表明,此算法具有良好的分辨力和测角精度。

波达方向估计; 非圆信号; 高阶奇异值分解; 张量; 旋转不变子空间算法

0　引　言

基于子空间的测向技术[1]由于高精度高分辨性能,备受人们关注。近年来,许多学者利用非圆信号的特性[2-3]来提高子空间算法的测向性能,且可测信源数也加倍。目前所提出的基于非圆信号的多重信号分类(multiplesignalclassificationfornon-circularsignals,NC-MUSIC)算法[4]和基于非圆信号的旋转不变子空间(estimationsignalparametersviarotationalinvariancetechniquesfornon-circularsignals,NC-ESPRIT)算法[5],其中NC-MUSIC算法需要进行谱峰搜索,计算量大,而NC-ESPRIT算法只需构造旋转不变关系,就能达到高精度高速率。文献[6]提出一种基于非圆信号的实值ESPRIT算法,该方法只适用于一维估计。在现代信息轰炸的时代,一维估计已经不再满足工程需求,需要将子空间算法向高维推广。而目前的二维ESPRIT算法多是拘泥于天线阵列的摆放形式[7-9],文献[10]提出的基于非圆信号的多维ESPRIT类算法,可以对空间多个频率进行联合估计,但估计精度一般。引入数学工具张量[11-12],可提高子空间算法对参数估计的精度和分辨力,且在计算过程中也能直观地体现阵列的结构,因此文献[13]提出了一种基于非圆信号的张量ESPRIT(tensorESPRITfornon-circularsignals,NC-TE)算法,但是张量之间的运算量较大；文献[14]提出了一种基于非圆信号的酉张量ESPRIT(unitarytensorESPRITfornon-circularsignals,NC-UTE)算法,此种方法要通过前向后向平均技术和双映射来转换成实值,所需的复数张量运算较为复杂。本文提出一种基于非圆信号的实值张量ESPRIT算法,该方法只是通过简单的加减法,即能转换成实值,既可保证测向精度,又能降低运算量。

本文首先介绍了张量分解的基本运算,然后从张量信号模型出发,根据欧拉公式,利用最大非圆率非圆信号的特点构造实值张量,最后通过构造旋转不变关系和特征分解,得到来波方向。通过实验仿真,验证了该方法的有效性。

1　数学模型

1.1张量的基本运算

假设存在一个M1×…×Mr×…×MR维的张量A与张量C,I×Mr维的矩阵U,I1×I2×…×IJ维张量D,其中r=1,2,…,R,张量可以看作为一个多维阵列,其具体的运算如下。

(1)r模式张量矩阵化

(2)r模式乘积

(3) 高阶奇异值分解

张量A的高阶奇异值分解可表示为A=S×1U1×2U2…×RUR,其中S是M1×M2×…×MR维的核心张量,Ur是[A](r)奇异值分解的Mr×Mr维的左奇异特征向量,其中r=1,2,…,R。

(4) r模式拼接

(5) 外积

张量A与D的外积,记为F=A∘D,它的维数为M1×M2×…×MR×I1×I2×…×IJ,其中fm1m2…mRi1i2…iJ=am1m2…mRdi1i2…iJ。

1.2张量接收数据模型

假设有q个远场窄带信号入射到R维阵列上,阵元数为M1×M2×…×MR,快拍数为L,则天线阵列接收的数据为

(1)

式中,X代表的是M1×M2×…×MR×L维的接收数据张量;A代表的是M1×M2×…×MR×q维的导向张量;S代表的是q×L维的观测信号;N代表的是M1×M2×…×MR×L维的零均值高斯白噪声张量。

根据张量的基本概念,可知接收数据矩阵中的各部分量与张量的关系为

(2)

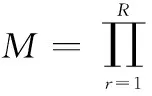
常见的最大非圆率非圆信号有二相相移键控(binary phase shift keying,BPSK)信号和幅度调制类的信号;最大非圆率非圆信号本身是实信号,但由于是调制信号,一般需要进行解调处理,受到信道的影响,会有相位的偏移,所以最大非圆率信号S[15]可以写为

(3)

式中,Φ=diag(ejφ1,ejφ2,…,ejφq),φi(i=1,2,…,q)是非圆相位;S0是实初信号。

2　算法原理

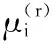
(4)

由于信号S0是实信号,根据欧拉公式构造阵列的接收数据矩阵为

(5)

式中,Yf,Yg是M×L维实值数据矩阵;Af,Ag是定义的M×q维的导向矢量矩阵,表达形式为

(6)

(7)

具体的每个导向矢量为

(8)

(9)

将接收数据的实部与虚部串联,得到重构接收数据矩阵为

(10)

3　实值张量ESPRIT算法

将矩阵推广到张量空间,应用到R维阵列,则构造的阵列接收数据张量为

(11)

式中,Yf,Yg是构造的M1×M2×…×MR×L维的实值数据张量;Af,Ag是定义的M1×M2×…×MR×q维的导向张量。

定义的导向张量Af,Ag分别为

(12)

(13)

对构造的实值数据张量,沿r模式加以拼接,进行扩增,则有R种不同的扩增方式

(14)

式中,Y(r)的维数为M1×…×Mr-1×2Mr×Mr+1×…×MR×L,其中r=1,2,…,R。

假设天线阵列的维数为2,利用欧拉公式构造正弦数据张量与余弦数据张量,根据阵列维数将其拼接,则具体的拼接形式如图1所示。

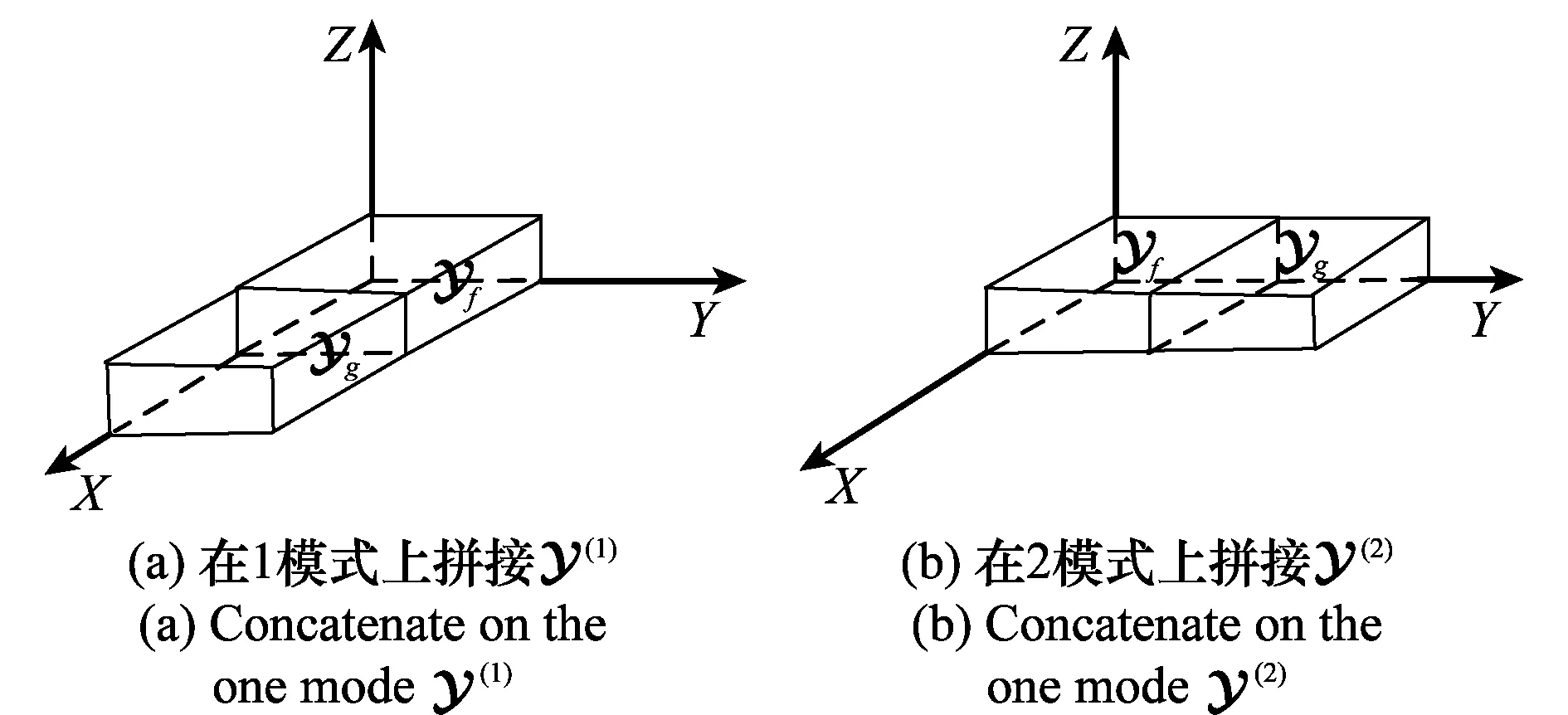
图1　接收数据张量的拼接方式Fig.1　The concatenate way of array receiving data tensor

(15)

为构造旋转不变关系,定义两个Toeplitz矩阵为

(16)

(17)

根据前面的Toeplitz矩阵,定义两个选择矩阵为

(18)

(19)

旋转不变关系为

(20)

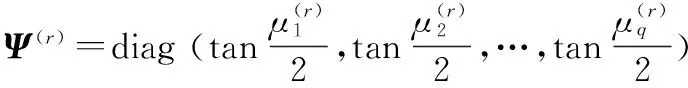
又因为导向张量A与信号张量U(r)[s]张成的是一个子空间,存在一个非奇异值矩阵Q,使得A=U(r)[s]×R+1Q,则有

(21)

(22)

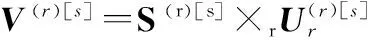
对式(22),利用张量R+1模式矩阵化,再根据最小二乘法可以得到

(23)

式中,(·)†代表的是广义逆。

对Ω(r)=QΨ(r)Q-1进行特征分解,得到

则有

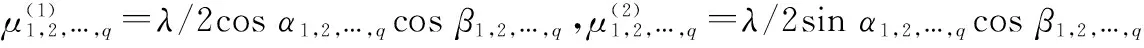
(24)

(25)

对二维来波方向估计,需要单独的两次特征值分解,但不能保证两次分解的特征值的位置一一对应,所以涉及到参数配对问题,本文采用文献[17]的方法进行配对。

4　运算复杂度分析

一个算法的运算量将直接影响到工程上的实时性,对整个工程系统的运作都会有直接的影响,因此分析算法的运算量至关重要。本文将比较NC-TE算法、NC-UTE算法与本文算法的运算量。

基于张量的ESPRIT类算法,由于张量属于不破坏阵列结构的高维运算,计算量的大小与阵列维数有直接的关系,而基于张量算法的计算量主要体现在对构造的阵列接收数据张量进行高阶奇异值分解上。高阶奇异值分解包括:首先需要对构造的阵列接收数据张量进行r模式矩阵化,然后对r模式化得到的矩阵做奇异值分解，得到左奇异值特征向量,最后利用构造的阵列接收数据张量与各个左奇异值特征向量的r模式乘积，得到核心张量。

所以高阶奇异值分解中,运算量主要包括张量矩阵化、奇异值分解及张量与矩阵的乘积。假设r模式拼接的阵列维数为M1×…×2Mr×…×MR×L,各算法的运算量统计如表1所示。

表1　3种算法的计算复杂度比较(r模式)

由表1分析可知,张量之间的运算量较大,本文算法与NC-UTE算法的运算量相当,在奇异值分解、张量与矩阵的乘积运算量上是NC-TE算法的1/4。

接下来比较本文算法与NC-UTE算法在构造实值上的运算量,如表2所示。

由表2分析可见,关于NC-UTE算法,在做高阶奇异值分解之前,转换成实值所涉及的前向后向平均技术和双映射,需要计算张量与矩阵的模式乘积,而本文算法只需简单的加减即可构造成实值,可见NC-UTE算法的运算量大于本文算法。

表2　2种算法构造实值的计算复杂度比较(r模式)

5　仿真实验

为了验证本文算法的有效性,进行了计算机仿真实验,并与NC-ESPRIT(NC-E)算法、NC-MUSIC(NC-M)算法、NC-TE算法、NC-UTE算法进行对比。

实验条件:信号频率f=3 GHz,采用7×7的均匀矩形阵列,阵元间距为入射信号的半波长,零均值的高斯白噪声,2个非相干信号源,入射信号的方位角为(20°,160°),对应的俯仰角为(80°,80°),每次仿真进行100次蒙特卡罗实验。定义测角均方根误差(root mean square error, RMSE)和成功分辨概率η为

(26)

(27)

实验 1角度估计。固定信噪比为20 dB,固定快拍数为100,利用本文方法进行来波方向估计,进行20次蒙特卡罗实验,并对两个信号进行局部放大,如图2所示。由图2可以看出,利用本文方法可以对两个信号的来波方向进行估计,且从两个信号的局部放大图可以看出,多次测向时估计偏差不大,说明了该方法的有效性。

图2　信号星座图及局部放大图Fig.2　Signal constellation and partial enlarged

实验 2测角精度。先固定信噪比为20 dB,比较本文方法与NC-TE算法及NC-UTE算法的测角RMSE随快拍数变化的关系,如图3所示;然后固定快拍数为100,比较本文方法与NC-M算法、NC-E算法、NC-TE算法及NC-UTE算法的测角RMSE随信噪比变化的关系,如图4所示。

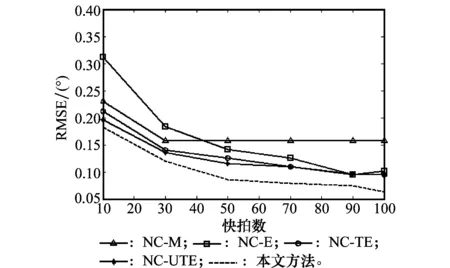
图3　快拍数对测角均方根误差的影响Fig.3　Influence of RMSE versus snapshots number

图4　信噪比对测角均方根误差的影响Fig.4　Influence of RMSE versus SNR

由图3和图4可以看出,这5种算法对两个信号的测角RMSE均随快拍数的增加而减小,随信噪比的提高而降低。从图3中可以看出,在信噪比固定的情况下,NC-M算法在快拍数为30时,性能基本稳定,此时的误差主要由搜索步长引起,但是该方法需要谱峰搜索,耗时较长;NC-E算法在快拍数为90左右,测向性能才与NC-TE算法及NC-UTE算法趋近,可见数学工具张量提高了测角性能;NC-TE算法及NC-UTE算法性能相当;在快拍数为50左右时,本文方法的测向RMSE基本保持不变了,且测向精度较高。从图4中可以看出,快拍数固定为100时,NC-M算法与NC-TE算法、NC-UTE算法及本文算法的性能相当,可见在快拍数为100时,这些算法的性能已经饱和。

实验 3成功分辨概率。先固定信噪比为20 dB,比较本文方法与NC-M算法、NC-E算法、NC-TE方法及NC-UTE算法对多个信号的成功分辨概率随快拍数变化的关系,如图5所示;然后固定快拍数为100,比较本文方法与NC-M算法、NC-E算法、NC-TE算法及NC-UTE算法对多个信号的成功分辨概率随信噪比变化的关系,如图6所示。

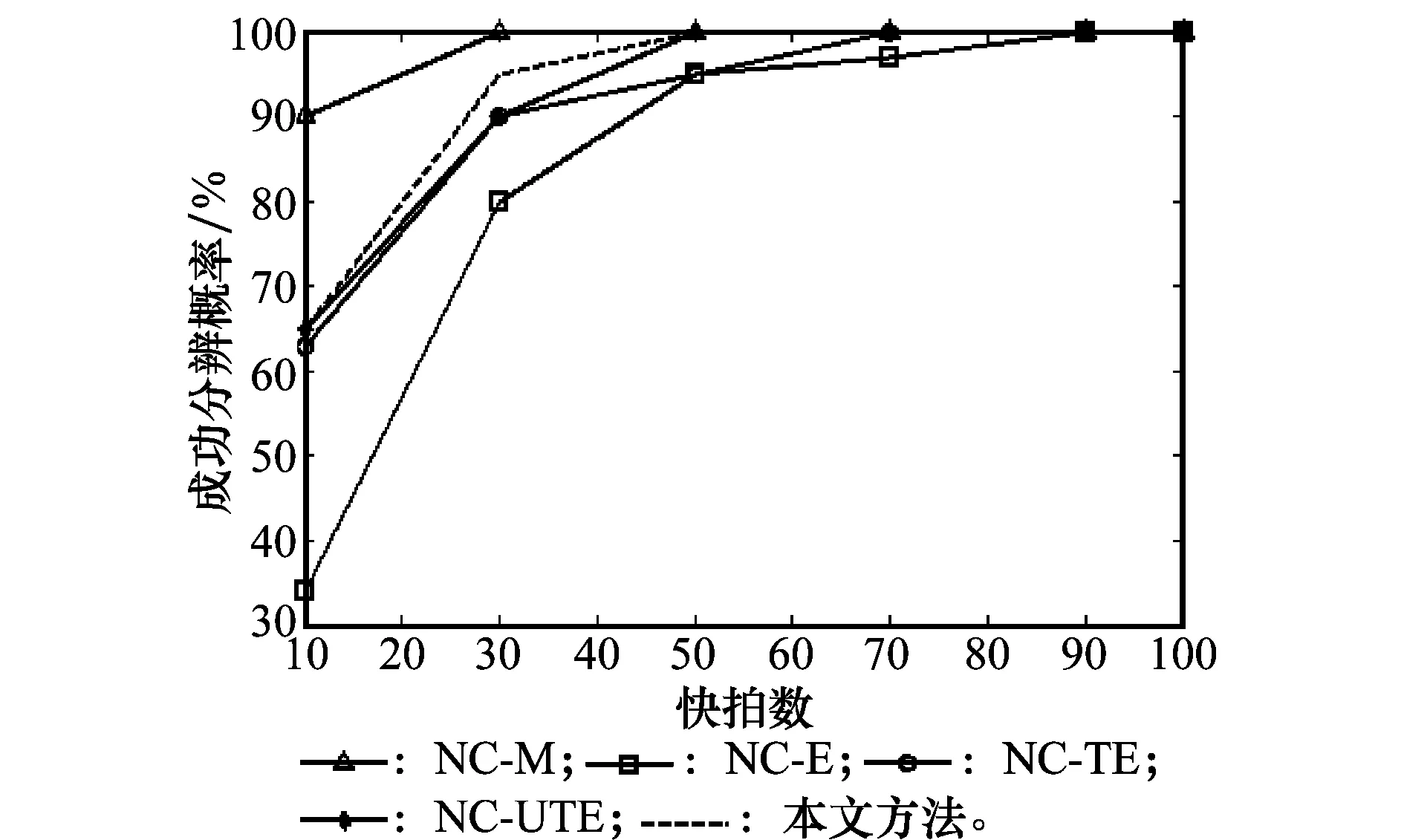
图5　快拍数对成功分辨概率的影响Fig.5　Influence of successful estimation versus snapshots number

图6　信噪比对成功分辨概率的影响Fig.6　Influence of successful estimation versus SNR

由图5和图6可以看出,在一定的快拍数与信噪比门限内,这5种方法对两个信号的成功分辨概率都随快拍数和信噪比的增加而提高。在信噪比固定为20 dB时,低快拍数下,NC-M算法的成功分辨概率最高,可见高信噪比下,NC-M算法优于其他算法；在快拍固定为100时,NC-M算法、NC-E算法的成功分辨概率要低于基于张量类的算法,可见数学工具张量提高了分辨性能。

6　结　论

本文推导了利用最大非圆率非圆信号的实值特点,通过欧拉公式构造两个实值接收数据张量,然后根据阵列维数对构造的两个实值接收数据张量以不同的方式拼接,最后借助高阶奇异值分解,实现波达方向估计。本文方法利用张量工具,提高多维信号参数估计性能,但同时张量也带来了较大的运算量,所以本文又通过欧拉公式将复数运算转化为实值运算,极大地降低了运算量,且保证了测向性能。仿真实验表明,相比较于NC-M算法、NC-E算法、NC-TE算法及NC-UTE算法,在一定程度上,本文方法提高了测角精度与分辨力,且实时性也较高。

[1] Yan F G, Shen Y, Liu S, et al. Overview of efficient algorithms for super-resolution DOA estimates[J].SystemsEngineeringandElectronics, 2015,37(7):1465-1475.(闫锋刚,沈毅,刘帅,等.高效超分辨波达方向估计算法综述[J].系统工程与电子技术,2015,37(7):1465-1475.)

[2] Yun M S, Lei H, Cheng Q. Direction-of-arrival estimation for noncircular sources via structured least squares-based ESPRIT using three-axis crossed array[J].IEEETrans.onAerospace&ElectronicSystems, 2015, 51(2): 1267-1278.

[3] Jian X, Hai H T, Xuan R, et al. Efficient method of passive localization for near-field noncircular sources[J].IEEEAntennasandWirelessPropagationLetters, 2015, 14: 1223-1226.

[4] Gounon P, Adnet C, Galy J. Location angulaire de signaux nonciculaires[J].TraitementduSignal, 1998, 15(1): 17-23.

[5] Zoubir A, Chargé P, Wang Y. Non circular sources localization with ESPRIT[C]∥Proc.oftheEuropeanConferenceonWirelessTechnology, 2003: 1-4.

[6] Zheng C D, Feng D Z, Zhou Y. A real-value algorithm of ESPRIT via exploitation of non-circular sources property[J].JournalofElectronics&InformationTechnology,2008,30(1): 130-133. (郑春弟, 冯大政, 周祎. 基于非圆信号的实值ESPRIT算法[J].电子与信息学报, 2008, 30(1): 130-133.)

[7] Tayem N, Kwon H M. L-shape 2-dimensional arrival angle estimation with propagator method[C]∥Proc.oftheIEEEVehicularTechnologyConference, 2005: 6-10.

[8] Diao M, Miao S L. New method of parameter matching for 2-D ESPRIT algorithms[J].SystemsEngineeringandElectronics, 2007,29(8):1226-1229.(刁鸣,缪善林.一种二维ESPRIT算法参数配对新方法[J].系统工程与电子技术,2007,29(8):1226-1229.)

[9] Liang H, Cui C, Dai L, et al. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J].JournalofElectronics&InformationTechnology, 2015, 37(8): 1828-1835. (梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J].电子与信息学报, 2015, 37(8): 1828-1835.)

[10] Steinwandt J, Roemer F, Haardt M. R-dimensional ESPRIT-type algorithms for strictly second-order non-circular sources and their performance analysis[J].IEEETrans.onSignalProcessing,2014, 62(18): 4824-4838.

[11] Kolda T G, Bader B W. Tensor decompositions and applications[J].SiamReview, 2009, 51(3):455-500.

[12] Jiang B, Ma S, Zhang S. Tensor principal component analysis via convex optimization[J].MathematicalProgramming, 2012, 150(2): 423-457.

[13] Haardt M, Roemer F. Higher-order SVD-based subspace estimation to improve the parameter estimation accuracy in multidimensional harmonic retrieval problems[J].IEEETrans.onSignalProcessing，2008, 56(7): 3198-3213.

[14] Roemer F, Haardt M. Multidimensional unitary tensor-ESPRIT for non-circular sources[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing, 2009: 3577-3580.

[15] Chen H, Zhu W P, Swamy M N S. Real-valued ESPRIT for two-dimensional DOA estimation of noncircular signals for acoustic vector sensor array[C]∥Proc.oftheIEEEInternationalSymposiumonCircuitsandSystems, 2015: 2153-2156.

[16] Lathauwer L D, Moor B D, Vandewalle J. A multilinear singular value decomposition[J].SIAMJournalMatrixAnalysis&Applications, 2000, 21(4): 1253-1278.

[17] Fan D, Zhang L, Wu Y. An improving ESPRIT algorithm by using two singular value decomposition[J].JournalofChinaInstituteofCommunications,2002,23(11):80-85.(范达,张莉,吴瑛.利用两次奇异值分解实现二维ESPRIT参量配对[J].通信学报,2002,23(11):80-85.)

Real-valuetensorESPRITalgorithmbasedoncharacteristicsofnon-circularsignals

SIWei-jian,YUFang,QUZhi-yu,MISheng-nan

(School of Information and Communication Engineering,Harbin Engineering University, Harbin 150001, China)

Basedonthecharacteristicsofnon-circularsignalsofthemaximumnon-circularrate,areal-valuetensorestimationsignalparametersviarotationalinvariancetechniques(ESPRIT)algorithmisputforward.Firstly,thearrayreceivingdatamatrixisextendedtotensorspacebystudyingtherelationshipbetweentensorandmatrix.Then,thearrayreceivingdatatensoristurnedintocosineandsinedatatensorbyusingtheEulerformula,accordingtothearraydimensionstoconcatenatecosineandsinedatatensorineachdimension,respectively,andobtainthesignalsubspacethroughahigher-ordersingularvaluedecompositionofreal-valueconcatenationtensordata.Finally,phasedifferenceisestimatedjointlyineachdimensiontorealizedirectionofarrival(DOA)estimationbyconstructingtheselectionmatrixandeigendecomposition.Theexperimentalsimulationresultsshowthatthisalgorithmhasabetterresolutionandanglemeasurementaccuracy.

directionofarrival(DOA)estimation;non-circularsignals;higher-ordersingularvaluedecomposition;tensor;estimationsignalparametersviarotationalinvariancetechniques(ESPRIT)algorithm

2015-12-07；

2016-04-14；网络优先出版日期：2016-06-26。

航空科学基金(201401P6001)；中央高校基本科研业务费专项资金(HEUCF150804)资助课题

TN911.7

ADOI:10.3969/j.issn.1001-506X.2016.09.02

司伟建(1971-),男,研究员,博士,主要研究方向为宽带信号检测、处理与识别，高分辨高精度无源测向、谱估计。

E-mail:swj0418@263.net

禹芳(1990-),女,硕士研究生,主要研究方向为宽带信号检测、处理与识别，非圆信号处理。

E-mail:yufang19900908@126.com

曲志昱(1983-),女,副教授,博士,主要研究方向为宽带被动导引系统中信号处理技术、宽带信号测向。

E-mail:quzhiyu@hrbeu.edu.cn

米胜男(1990-),女,硕士研究生,主要研究方向为宽带信号检测、处理与识别。