基于MatLab/Simulink的EPS系统参数的优化仿真

贾满满

(商丘师范学院 物理与电气信息学院 河南 商丘 476000)



基于MatLab/Simulink的EPS系统参数的优化仿真

贾满满

(商丘师范学院 物理与电气信息学院 河南 商丘 476000)

大多数汽车电动助力转向系统(EPS)控制器使用PID控制，而控制器参数设计通常使用试凑法反复试验来确定，所以汽车操纵的轻便性和灵活性不可能达到最优.针对这种情况，提出了用单纯形法设计EPS系统控制器参数，寻找优化设计的目标函数.运用MatLab控制工具箱建立系统模型并进行了Simulink仿真实验研究，仿真实验结果表明.运用单纯形法设计EPS系统控制器能够较大的提高其时域响应，提高了汽车操纵的轻便性和灵活性，并为优化设计提供了理论依据.

电动助力转向；单纯形；PID；Simulink仿真

0　引　言

电动助力转向系统(EPS)是靠电动机来提供辅助助力，助力的大小受电子控制单元(ECU)控制，从而控制电动机的输出力矩实现转向助力.EPS控制系统的参数优化设计是在被控对象和控制器已知的条件下，经过在线调节控制器的参数，使EPS控制系统达到优化的目的.本文为了提高EPS系统的时域响应，提高汽车操纵的跟踪性和轻便性，避免控制器参数优化设计使用试凑法反复试验来确定的弊端，通过分析EPS系统并依据牛顿定理建立其数学模型，然后采用单纯形法对EPS的PID控制器参数进行优化设计.

1　EPS数学模型的建立

EPS的机械部分如图1所示，简化后由电机组件、方向盘转向柱组件和齿轮齿条组件组成.忽略各种非线性摩擦并根据牛顿运动定律建立运动方程，得到整个系统的数学模型[1,2].

(1)

(2)

(3)

图1　EPS系统动态结构模型

对上式进行变量定义.Jc与Jm分别是转向盘转向柱转动惯量与电机子系统转动惯量；θc与θm分别是转向盘转动的角度与助力电机的转动角度；kc与km分别是转向柱刚度与电动机系统管柱刚度；xr和m是转向横拉杆的位移和质量；bc、bm和b分别是转向盘转向柱子系统阻尼系数、电机系统阻尼系数及转向横拉杆系统阻尼系数；rp是转向小齿轮的半径；G是齿轮传动比；FTR为转向横拉杆作用力；Td与Tm分别为方向盘输入扭矩、电动机输出扭矩[3-5].

2　电动助力转向系统控制器参数优化

2.1传统PID控制参数确定方法

PID控制器是把偏差的比例P、积分I与微分D由线性组合组成控制量，对被控对象进行相应的控制.其控制规律为：

(4)

式中比例环节成比例地反映控制信号的偏差信号e(t)，如果偏差出现，控制器会产生控制作用来减少偏差.积分环节可以消除静差，积分时间常数TI决定积分环节的强弱，当TI越大时，积分作用会越弱.微分环节决定偏差信号的变化速率，会在偏差信号变的太大前在控制系统中加入修正信号，进而减小调节时间.

由于EPS是有差系统，为了保持系统的静差，在应用中控制器采用不完全的PID控制，也即P控制或PD控制.当比例系数太大时，系统可能发生等幅振荡，甚至出现发散振荡；反之，系统会越稳定.微分输出的方向会阻止被控变量的变化，使偏差不变，因此，当被控变量发生剧烈的变化时，能在剧烈变化发生瞬间，提供较大的调节作用，减少被控变量的波动幅度.

控制器参数确定的方法通常有经验法、半经验法、反应曲线法和理论计算法.

(1)经验法可先设置比例度，确定系统的振荡周期Tp，接着根据被控过程的特点，当采用PI控制时，设置Ti=(0.5-1)Tp;对成分、温度等被控过程，可采用PID控制，设置Td=(0.25-0.5)Ti.即比例度从大到小搜索，直到过渡过程符合控制要求.

(2)半经验法先用单纯P作用搜索，得到所需衰减比的响应曲线，接着根据相应的振荡周期和参数等数据，用半经验公式计算PI或PID控制器的参数.

(3)反应曲线法和理论计算法得出控制器参数.

经验法和半经验法通过闭环运行观察系统的响应曲线，通过反复试凑参数达到满意的结果，确定PID的控制参数.此方法有一定的局限性，因为需要反复试验，控制效果也可能达不到最优.反应曲线法和理论计算法通过大量计算得到控制器参数，参数最优值的确定有一定的困难.通过目标函数对控制系统PID参数的优化能解决参数最优问题，本文EPS系统的PID控制器参数的确定采用单纯形法寻优.

2.2目标函数的选取

单纯形是变量空间内最简单的规则形体.在如图2所示的二维空间取平面上的三个点构成单纯形.单纯形的寻优过程为[7]：

(1)△XYZ的X点是坏点，便抛弃X点，并把三角形YZ沿边翻转，可得到新△X1YZ.不断重复此过程，就是抛弃坏点，并建立新点.如果坏点重复，就抛弃次坏点，并接着上述过程.

(2)当三角形接近峰顶(即最优值)时，会发生三角形绕相同“好点”转圈的情况，即好点重复出现.假如单纯形绕最优点翻转的次数用T表示，变量的维数用N表示，当T≥1.65N时表示三角形达到峰顶.

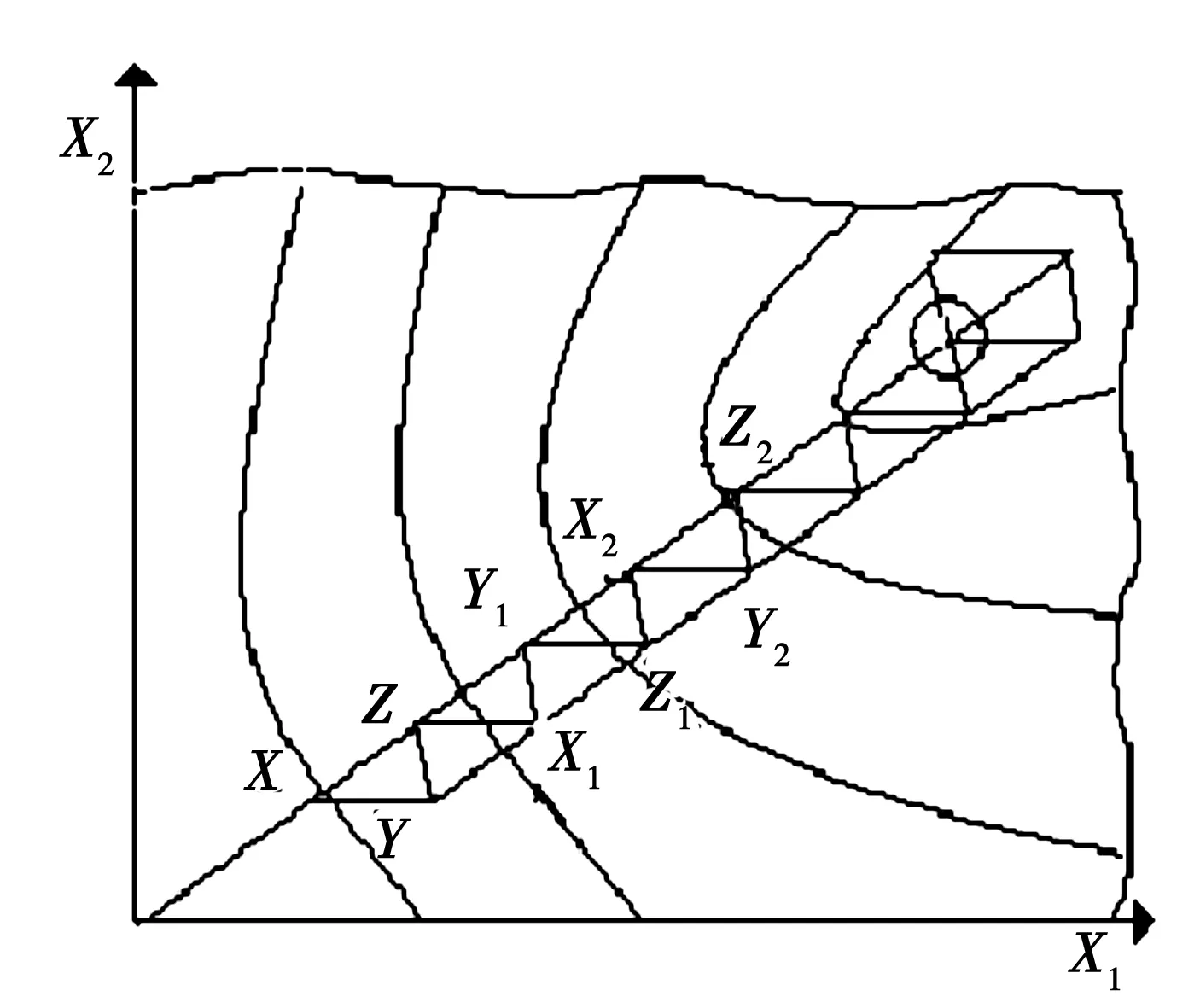
图2　单纯形法寻优原理

图3　控制系统调节器参数优化设计原理图

(3)假如对变量的精度要求比较高，可先把单纯的边长值缩小，然后接着寻优过程，一直到满意的参数.单纯形法求出的“好点”为最优设计方案，求出的变量值即为最优参数.

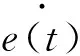
(5)

EPS系统利用单纯形法仿真流程图如下图4所示：

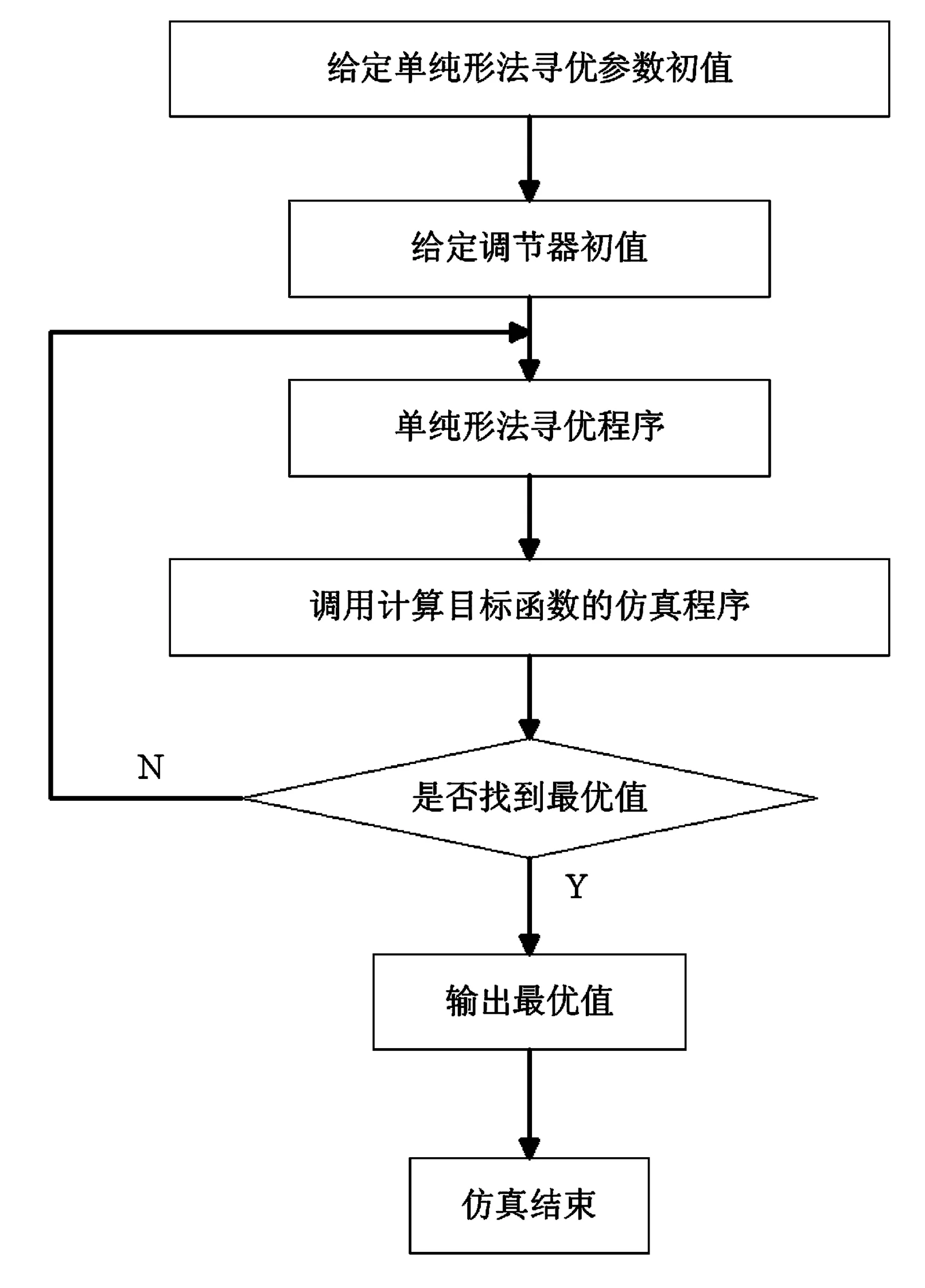
图4　单纯形法参数寻优程序框图

3　仿真实验结果分析

在SIMULINK中搭建EPS系统的仿真模型并进行仿真分析，如图5所示.

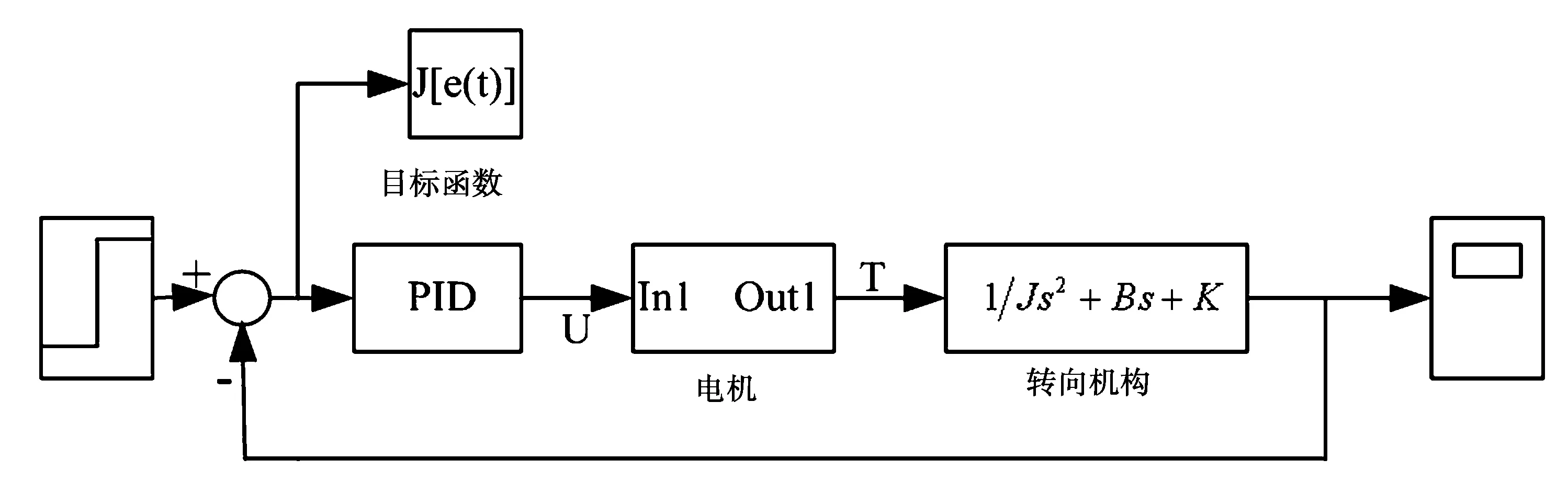
图5　EPS系统仿真模型

在MATLAB的命令窗口中运行程序可以得到优化后的参数，如表1所示.

表1　目标函数优化后所得系统参数

当采用比例微分控制时，选取kp=20,kd=1.在原来机械转向系统中加入了比例控制和比例微分控制，并分别用单纯形法进行参数的优化设计.其仿真曲线如图6所示，可以看出，优化后EPS系统的仿真曲线减小了超调量，系统的稳定时间也缩短了.仿真曲线结果表明EPS系统具有良好的跟踪性和稳定性.

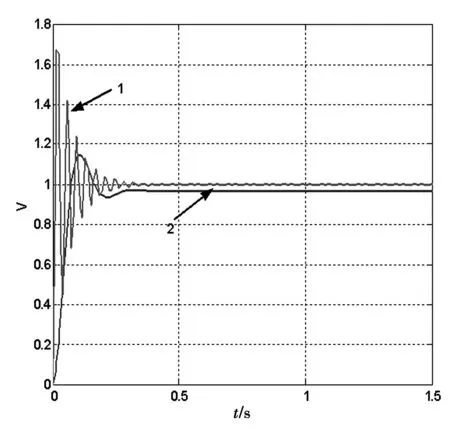
图6　比例微分控制下系统的阶跃响应(1是优化前，2是优化后)

4　结　论

EPS系统的助力性能直接关系到汽车的转向操纵性能.EPS系统的助力性能影响转向行驶的安全性，转向助力性能的好坏是由跟踪性与稳定性决定的.本文将单纯形法的寻优原理与PID控制相结合应用于EPS控制系统，仿真结果表明，设计的PID参数优化控制器可使EPS系统具有良好的跟踪性与稳定性，同时也为EPS系统的设计提供了理论依据.

[1]孟涛,陈慧,余卓平,等.电动助力转向系统的回正与主动阻尼控制策略研究[J].汽车工程,2006, 28(12):1125-1128.

[2]赵万忠,施国标.基于实时小波去噪方法的EPS电流跟踪控制[J].汽车工程,2008,30(3):227-230.

[3]Ji-Hoon Kim, Jae-Bok Song.Control logic for an electric power steering system using assist motor[J].Mechatronics,2002,12(5):447-459.

[4]周洪彦,杨润生,周发琳,等.模糊神经网络在发电机励磁控制中的应用[J].军械工程学院学报, 2008, 20(5):58-62.

[5]尚喆,许镇琳,王豪.基于神经网络的电动转向系统助力特性研究[J].汽车工程,2004,26(3):319-321.

[6]刘照，杨家军，廖道训.基于混合灵敏度方法的电动助力转向系统控制[J].中国机械工程，2003(5):874-876.

[7]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社,2003:49-59.

[责任编辑：徐明忠]

Optimal simulation of EPS system parameter based on MatLab/Simulink

JIA Manman

(College of Physics and Electrical Information, Shangqiu Normal University, Shangqiu 476000,China)

PID control is used by most of the electric power steering controllers, parameters design of controllers is determined by making experiments again and again, so portability and flexibility of vehicle steerering is probably unable to achieve optimization.To deal with this situation, a method is presented for designing parameters of system controller using simplicity shape algorithm, and looking for self-optimizing objective function.Using matlab control toolbox to establish the system model and simulation experiments on simulink.The result of simulation experiments showed that using simplicity shape algorithm to design EPS controller can enormously improve the time domain performance, can improve portability and flexibility of vehicle steerering, and provide a theoretical basis for optimal design.

electric power steering; simplicity shape algorithm; PID; simulink simulation

2016-01-09

商丘师范学院青年科研基金(2011QN13)；河南省教育厅科学技术研究重点项目(12B140012,13B140191).

贾满满(1983-)，女，河南商丘人，商丘师范学院助教，硕士,主要从事控制理论与应用的研究.

TP391.9

A

1672-3600(2016)09-0030-03