一类空间直线方程问题的多种求解方法

刘春辉

（赤峰学院数学与统计学学院，内蒙古赤峰024000）

一类空间直线方程问题的多种求解方法

刘春辉

（赤峰学院数学与统计学学院，内蒙古赤峰024000）

综合运用空间解析几何、微积分、线性代数和向量代数的思想及运算技巧，讨论一类空间直线方程的求解问题，从不同角度给出了解决该类问题的多种方法.

空间解析几何；直线方程；向量

1　引言

空间直线作为空间曲线的一种最特殊和最简单的类型，是高等数学[1]课程体系中关于空间解析几何与向量代数内容的重要组成部分.在这部分内容中，空间直线方程的求取毋庸置疑的是问题的核心和基础.同时，纵观种类繁多的关于高等数学和空间解析几何[2]的教材和教学参考书，其中不乏对空间直线方程求解问题的分析和讨论.就同一类问题而言，如果从多角度多侧面去进行分析，不但可以得到多种不同的解决问题的方法，而且也有助于培养学生综合运用知识的思维能力和创新能力.

鉴于此，本文针对如下一类空间直线方程的求解问题，从多个角度进行分析和思考，获得了该类问题的多种解决方法.

问题设空间直线l经过空间一点P(x0,y0,z0)且与两平面的交线平行，求直线l的方程.

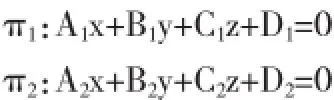
2　问题的多种解决方法

分析已知条件，不难看出问题的关键在于确定直线的方向向量s=(m,n,p)，从而得到l的点法式方程：方法一利用向量积的特征求直线方程因为平面π1和π2的法向量分别为：

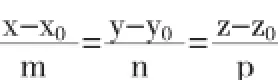
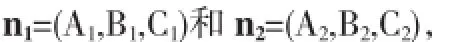
且l与平面π1和π2的交线平行，所以l的方向向量s必同时与π1和π2的法向量垂直，即

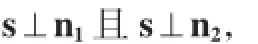
故根据两个向量向量积的特征，可取

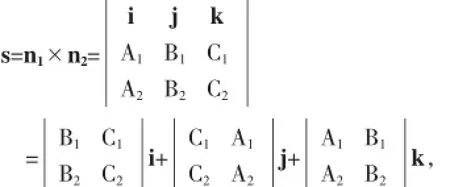
于是可得l的方向向量

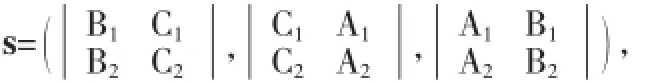
因此，空间直线l的方程为

方法二利用解线性方程组的Gramer法则求直线方程

引理1[1,2]设向量a=(a1,a2,…,an)，b=(b1,b2,…,bn)则a⊥b当且仅当a·b=0当且仅当a1b1+a2b2+…+anbn=0.

引理2[3](Gramer法则)设一个含有n个未知量n个方程的线性方程组为

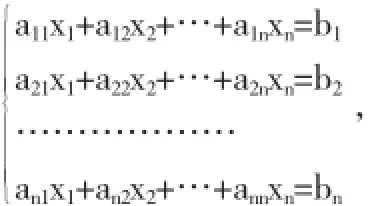
它的系数行列式为

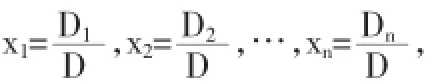
其中Dj是把行列式D的第j列的元素换以方程组的常数项b1,b2,…,bn而得的n阶行列式.

下面利用Garmer法则给出所讨论问题的另一种解决方法：

因为平面π1和π2的法向量分别为：

且l与平面π1和π2的交线平行，所以l的方向向量s必同时与π1和π2的法向量垂直，即

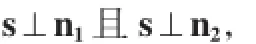
故由引理1，可得以m,n,p为未知量的方程组

当D≠0时，该方程组有且仅有一个解

又因为π1∩π2≠Ø，n1⊥π1且n2⊥π2，所以n1与n2不平行，从而它们的对应分量不成比例，不妨假设

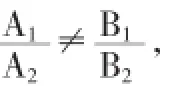
于是将方程组（1）中未知量p看成任意常数，变形得以m,n为未知量的方程组

其系数行列式

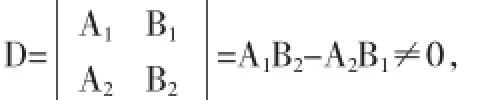
故由Garmer法则知，方程组（2）有唯一解

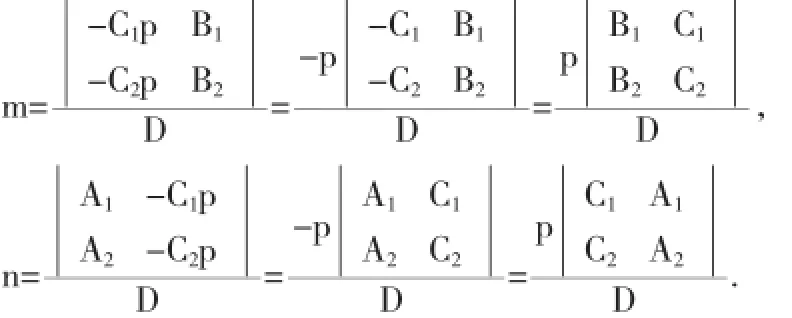
注意到常数p的任意性，令

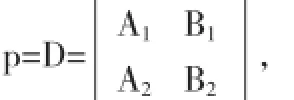
便得l的方向向量

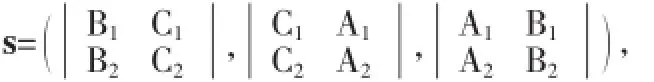
因此，空间直线l的方程为

点M(x0,y0,z0)∈Γ，又设三元函数F和G对各个自变量x,y,x都具有连续的偏导数且雅可比行列式

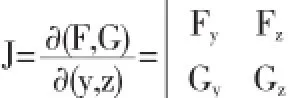
方法三利用隐函数组的存在性求直线方程引理3[1]设空间曲线Γ的一般方程为

满足J|M≠0，则在点M的某个邻域U(M)内，由(3)式可唯一的确定一组一元函数

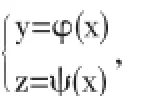
且Γ上任意一点P(x,y,z)处的切向量为

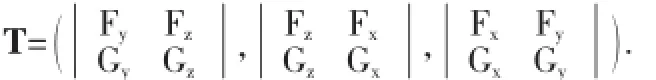
下面利用引理3给出所讨论问题的另一种解决方法：

首先令

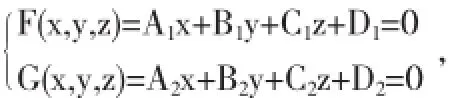
因为π1∩π2≠Ø，n1⊥π1且n2⊥π2，所以n1与n2不平行，从而它们的对应分量不成比例，不妨假设

则雅可比行列式满足

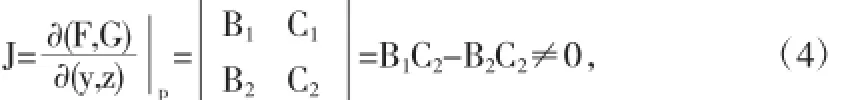
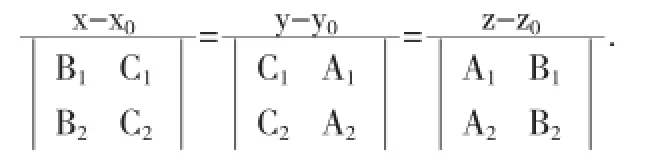
故由引理3得l的方向向量

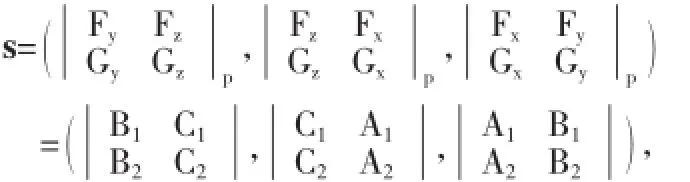
因此，空间直线l的方程为

注在上述过程中，如果（4）式满足J=0，而由π1∩π2≠Ø，n1⊥π1且n2⊥π2知

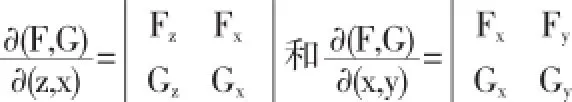
在P点处的值至少有一个不为0，因此利用引理3同样类似可得上述结论.

至此，我们分别利用向量积的特征、Garmer法则和隐函数组的存在性获得了解决所论问题的三种方法，最终都得到了直线的点法式方程的求解公式.如果考虑到两个平面平行的特征，还可获得所论问题的一种更简单的解决方法.

方法四利用空间平面平行的特征求直线方程

引理4[1,2]设空间两个平面为

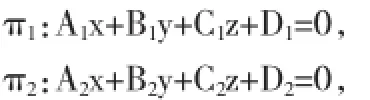
则π1与π2平行的充要条件是

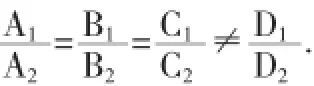
利用引理4给出所讨论问题的一种更简单的解决方法：

因为过点P(x0,y0,z0)且平行于平面π1：A1x+B1y+C1z+D1=0的平面为

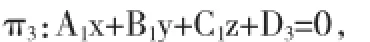
其中D3=-(A1x0+B1y0+C1z0)且D3≠D1.

过点P(x0,y0,z0)且平行于平π2：A2x+B2y+C2z+D2=0的平面为

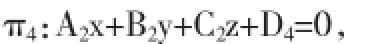
其中D4=-(A2x0+B2y0+C2z0)且D4≠D2.又因为π1∩π2≠Ø，所以π3∩π4≠Ø.

因此，注意到P(x0,y0,z0)∈π3∩π4便得平面π3与π4的交线即为所求直线l，即空间直线l的方程为

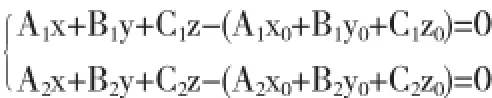
3　结束语

通过上述讨论，不难看出，虽然四种方法考虑问题的角度与出发点各不相同，但是殊途同归，最终获得的结论是一致的，这正是数学问题一题多解的精髓所在.问题的思考与解决的过程，不仅可以让我们不断开拓思维，使思考问题的思路更加灵活，而且有助于我们进一步理清前后知识的脉络，达到融会贯通的效果.

〔1〕同济大学数学系.高等数学：下册[M].第七版.北京:高等教育出版社,2014.

〔2〕李养成.空间解析几何[M].新版.北京:科学出版社,2007.

〔3〕王萼芳,石生明.高等代数[M].北京:高等教育出版社, 2003.

O182.2

A

1673-260X（2016）03-0003-02

2015-12-09