复杂网络模型发展综述

盛　夏

（吉林建筑大学城建学院，吉林长春130111）

复杂网络模型发展综述

盛夏

（吉林建筑大学城建学院，吉林长春130111）

复杂网络是近年来新兴的热门交叉科学,本文综述了复杂网络的诞生和发展,介绍了复杂网络模型的相关概念及其分类,例举了一些具有实际意义的常见复杂网络模型.通过近年来国内外科学家对复杂网络的一些相关研究,展望了未来复杂网络的一些发展方向.

复杂网络；小世界；无标度；动力学

网络自问世以来就受到了科学家们的关注,它是一种由数学中的图论演变出来的新兴交叉科学. 20世纪美国斥巨资建立的覆盖整个北美大陆的巨大电力系统网络却因一个小事故导致纽约900万居民经历了25小时的大规模停电,损失达3500万美元.其根本原因是当时人们对此类电力网络的复杂结构认识并不够清,不能规划出一个可以处理个别紧急突发状况的系统[1].由此看来,正确的认识复杂网络,并对其进行有效的管理和利用成了人们关心的问题.

1　网络的发展历程

1736年,Euler Leonhard提出了著名的“欧拉图问题”,即基于哥尼斯堡七桥问题:由4个点和7条线构成的一个图,从任一点出发经过每条边一次而后回到原点的回路是否存在？[2]这实际就是网络的前身——图.自此,图论成为数学的一个重要分支而被广泛的应用到各种社会科学以及自然科学等领域.从某种意义上来说,在网络发展的初期,图论的完善也意味着网络科学的发展[1].

20世纪50年代末和60年代间,Erdös和Renyi创立的正式的随机图论意味着网络发展迎来了第二次标志性突破.这是一种用相对简单的随机图来描述网络的方法,简称ER.该理论利用图论的阈函数、分支涌现的相变等为网络研究提供了重要的数学基础[2],引领了网络研究40年之久.然而,随机图并不是“全能”的,生活中我们真正接触到的各类网络不是都能用随机图简单描述清楚的.如,60亿人口中任意两个人相互认识的概率仅有6000万分之一[1],而实际上这两个人互相认识的几率会远比这个大的多.由此看来,随机图论并不适合描述非完全随机的网络.

1998年,Watts和Strogatz发表的“小世界网络的群体动力行为”和1999年Barabási和Albert发表的“随机网络中标度的涌现”则标志着复杂网络的研究进入了一个全新的时代.前者描述了从完全规则网络到完全随机网络的转变,后者则是揭示了复杂网络连接度分布的幂律特性,发现了复杂网络的无标度性质[2].

2　复杂网络的一些基本知识

2.1基本概念

大部分实际系统都是由相互作用的一组基本单元构成,忽略单元的基本结构,将它们看成一个个简单节点;同时忽略节点之间的复杂作用,将其抽象成基本单元之间的链接,这就构成了一个图.

网络可以描述成一组节点和一组边构成的图G,其中一个节点与边的阶梯序列u=v0e1v1e2…vn-1envn称为G的一条路径,v0和vn分别为起点和终点,路径中的边数称为路径“长”.节点v0和vn间最短的一条路径称为“最短路径”,其长称为“距离”.将网络中所有节点间“距离”的平均值定义为网络的平均路径长度,它是衡量网络全局性特征的量[3].

节点度指结点i的度ki表示与此节点直接相连接的边的个数.一个图的平均度k是网络中所有节点的平均连接数.结点度越大的节点在网络中越重要.度分布指一个随机选择的节点具有k条边的概率,也等于网络中度为k的结点数占网络结点总数的比值[4].

聚类系数是描述网络中节点之间结集程度的量.一个节点的聚类系数是它的所有邻接节点相互间实际存在的连接数与最多可能存在的边数的比值.将所有节点的聚类系数的平均值定义为网络的聚类系数,它是网络的局部特征.

2.2网络的主要分类

依据不同网络的动力学及统计学特性,将网络分为规则网络、随机网络和复杂网络,其中复杂网络又分为自相似、小世界和无标度网络.而规则网络和随机网络的特性相对单一,其研究价值不及复杂网络.

2.2.1小世界网络

小世界网络既像规则网络有较高聚类系数,又像随机网络有较短的平均路径长度.从图的角度说,就是大部分的节点不与彼此邻接,但任一节点可以经过少数几步到达其他节点[3].

实际网络是极其复杂的,而非一成不变的,一些细节上的小变化可能影响到整个网络特征的变化.适当的添加少量的长连接可以减小平均路径长度,同时聚类系数却不会产生很大的变化,使得一般规则网络逐渐演变成小世界网络.这种方法常被人为的利用,以此达到提高整个网络工作效率的目的. WS模型和NW模型就是小世界网络的典型例子.

2.2.2无标度网络

在无标度网络中,大部分节点只和少数几个节点连接,而有些节点与非常多的节点连接,这些关键节点被称为集散节点.集散节点拥有的连接可以成百上千,这也反映了网络中边分布的不均匀性,即无标度性.

集散节点使得网络对意外故障的发生具有强大的承受能力,但面对协同式攻击则显得非常脆弱.前者如同电力系统网络,只保护好重要的“枢纽”,那么一般小故障不会对全局造成大影响,也就不会出现开篇提到的大规模停电情况;而后者则如互联网络中的黑客攻击以及病毒传播,无差别攻击或者传播会造成全网瘫痪.具有代表性的无标度网络有BA模型、BBV模型等.

3　一些常见的复杂网络模型

3.1计算机网络

Internet网络可以看作是有许多计算机通过光、电缆等相互连接起来的网络系统,其中节点是单独的计算机或路由器,它们之间的物理连接看作边.而运行于Internet上的万维网也是一个复杂网络系统,节点代表网页,边则是网页之间的超文本连接,如图1[5].

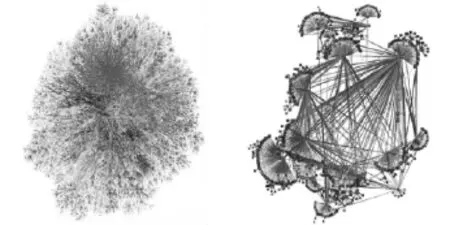
图1　计算机网络和WWW网络结构示意图

3.2交通网络

交通网络包括公路交通网络、铁路交通网络和航空交通网络.网络中的节点代表车站、机场等,而边则是连接不同站点之间的公路、铁路和航线等.

图2　美国高速公路和航空网络示意图

3.3生物网络

将生物体内新陈代谢中所涉及的化学反应物看成节点,而把反应需要的物质之间用边连接起来就构成了新陈代谢网络.基因网络是将基因看成节点,发生表达则是建立了不同基因之间的连接.生物网络还包括蛋白质网络、生物神经网络、食物链网络等.

3.4社会网络

社会网络是社会个体之间在相互接触过程中,按照某种组织形式和联系而形成的一个整体,包括个人之间的友谊网络、公司之间的业务网络等.其中节点可以是单个人或者公司,连接则是人与人之间的社会关系或公司之间的业务联络.演员网络、科研合作网络、论文的引用网络都属于社会网络.

4　近年来复杂网络的一些研究课题

4.1复杂网络的疾病传播

传染病的研究是复杂网络传播理论的一个重要课题,包括Internet上的病毒传播、人类社会中的SARS和艾滋病传播等.通过对特殊疾病在给定网络上的传播建立合适的数学模型,研究传染病在网络上的传播规律,从而给出防、病治病的方法.假设染病个体位于一个复杂网络的节点上,传播只能通过边进行,而传染效率由传播率来决定.在均匀网络中,存在一个传播阈值lc,当传染率l

4.2复杂网络的动力学同步

同步指性质相近的动力系统间通过相互作用,使它们在不同的初始条件下演化成状态逐步接近的动力系统,最后达到完全相同的状态并保持稳定.随着小世界网络和无标度网络的建立,对复杂网络同步的研究也迅速发展起来,主要的研究工作包括:网络上动力系统同步的稳定性分析,复杂网络结构与同步能力之间的关系,提高网络同步能力的方法,复杂网络上动力系统的同步控制等[8].

4.3复杂网络的控制

控制是通过有选择地对网络中的部分节点施加控制而使整个网络具有期待的行为,其中研究的关键是控制的可行性和有效性.可行性是指复杂网络是否可控;有效性则是尽量降低控制的代价达到控制目标的效果.2011年Liu,Barabási等基于线性系统控制理论建立了复杂网络可控制的理论模型,发现任意控制网络中的最有影响力的节点对整个网络控制的影响最大[9].

4.4复杂网络的结构识别

目前,动力网络大多研究网络拓扑结构已知条件下网络动力学的控制与同步等问题,或网络结构的各种特征参数对网络动力学的影响.而实际模型中复杂网络存在各种不确定的信息,往往只有部分已知网络的结构和节点动力学,拓扑连接、耦合时滞分布等,并且在基因表达网络、能量网络和生物神经网络中随时空变化.因此动力网络结构的识别问题有着广泛的实际背景,它也是分析、控制和预测实际的真实网络动力学行为的先决条件[10].

4.5复杂网络的鲁棒性

鲁棒性指网络中的部分边或者节点被破坏时,仍能维持其功能的能力.静态鲁棒性指删除网络中部分节点时,不需要对节点或边进行重新分配,仍保持功能的能力;而动态鲁棒性则是当部分节点发生破坏时,网络流需要重新分配,经过动态平衡后,仍维持功能的能力.网络类型的不同决定了面对各种破坏的不同鲁棒性,如无标度网络对随机破坏具有高度的鲁棒性,但对于蓄意破坏网络中度较大或者介数较大的节点网络的鲁棒性较差;而随机网络的容错能力和抗毁能力则大致相同[10].

5　前景展望

前文所述,网络的研究中涉及到了拓扑结构、混沌控制、动力学理论、统计学知识,甚至是计算机模拟等多方面的研究.而对于不同类别实例的系统了解上又体现出了多学科交叉的特点,而未来,复杂网络的研究领域将会涵盖的更广.今后的一段时间的研究还会围绕复杂网络动力学控制以及复杂网络的结构识别来进行,而小世界网络和无标度网络仍会是复杂网络界的“宠儿”.

〔1〕Watts D J.Six degrees:The science of a connected age[M].WW Norton,2004.

〔2〕方锦清.网络科学的诞生与发展前景[J].广西师范大学学报:自然科学版,2007,25(3):2-6.

〔3〕WangXF,ChenG.Complexnetworks: small-world,scale-free and beyond[J].Circuits and Systems Magazine,IEEE,2003,3(1):6-20.

〔4〕刘涛,陈忠,陈晓荣.复杂网络理论及其应用研究概述[J].系统工程,2005,23(6):1-7.

〔5〕林海.复杂网络若干动力学问题的研究[D].厦门大学,2007.

〔6〕Pastor-SatorrasR,VespignaniA.Epidemic spreading in scale-free networks[J].Physical review letters,2001,86(14):3200-3203.

〔7〕Kitsak M,Gallos L K,Havlin S,et al.Identification of influential spreaders in complex networks[J].Nature Physics,2010,6(11):888-893.

〔8〕Zhao M,Zhou T,Wang B H,et al.Enhanced synchronizability by structural perturbations[J].Physical Review E,2005,72(5):057102.

〔9〕Liu Y Y,Slotine J J,Barabási A L.Controllability of complex networks[J].Nature,2011, 473(7346):167-173.

〔10〕汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].清华大学出版社有限公司,2006.

O175.13

A

1673-260X（2016）03-0008-03

2015-11-25