弹塑性SDOF体系地震输入归一化等效速度谱

屠冰冰

弹塑性SDOF体系地震输入归一化等效速度谱

屠冰冰

（西安科技大学理学院，西安710054）

为了确定弹塑性单自由度（single degree of freedom，SDOF）体系地震输入能，分析了中美场地土剪切波速转换关系，将从美国PEER地震记录数据库选取的220条强震记录按中国场地土类型进行分类，基于能量平衡原理，采用归一化方法，建议了一种基于复合强度指标的弹性SDOF体系三段式等效速度谱.分析了5类场地土条件下SDOF体系系统参数对地震输入等效速度谱的影响.研究结果表明:刚度折减系数对等效速度谱无明显影响；延性系数和阻尼比增大均对等效速度谱峰值和下降段衰减速度有削弱作用.综合考虑各类影响因素，通过参数多次拟合，得出弹性SDOF体系归一化等效速度谱峰值段及下降段修正系数，提出了一种适用于我国场地土类型、可直接供设计使用的弹塑性SDOF体系归一化等效速度谱确定方法，并验证了其有效性.

SDOF体系；等效速度谱；能量

基于能量抗震设计理论主要是从能量平衡角度出发，融合力和位移这两个重要的结构设计参数，分析地震作用下能量的输入、转化和耗散，从而控制能量的转化途径［1-2］.基于能量抗震设计方法弥补了基于承载力设计方法不能考虑弹塑性位移和基于位移设计方法不能考虑结构累计损伤的不足，能够全面反映地震作用对结构的影响.1956年，Housner［3-4］首先提出基于能量抗震设计方法的概念，并给出抗震设计的性能指标；2014年，叶列平等［5］系统总结了建筑结构基于能量抗震设计方法的相关研究成果.在基于能量抗震设计方法中单自由度（SDOF）体系的地震输入能量谱是首先需要解决的基础问题.

SDOF体系地震输入能量谱问题的研究，最早是基于SDOF体系弹性，之后才是弹塑性SDOF体系，所提出的地震输入能量谱简化形式有两段式和三段式2种.Akiyama［6］将地震输入能量谱简化为两折线形式，但该种简化形式将对结构长周期地震输入能量产生过高估计；肖明葵［7］提出将弹性和弹塑性地震输入能量谱简化为双折线形式，并给出拟合公式和相应参数取值，但短周期段和长周期段误差较大；刘哲峰等［8］根据反应谱理论的思想，提出三段式简化能量谱（β谱简化计算模型），但仅对线性SDOF体系进行了讨论，未考虑非线性情况；程光煜等［9］、陈清军等［10］均以阻尼比 ξ=0.02的弹性SDOF体系为基础，给出了弹性和弹塑性SDOF体系的三段式简化能量谱，但所选地震记录是按美国场地土进行分类，不符合中国规范中的场地土类别；周云等［11］提出的三段式简化能量谱考虑了地震动三要素和结构阻尼对能量谱的影响，但参数确定复杂，不便于工程应用；何利等［12］建议了一种基于复合强度指标的三段式弹性输入能量谱，但只考虑了强度折减系数和阻尼比对能量谱的影响.由此可见，目前已有研究存在以下不足:

1）多是基于美国场地土类型，不便于我国工程设计人员直接使用.

2）定量研究较少，已有定量结果由于简化能量谱形式复杂、参数确定困难等原因不便于实际工程应用.

本文分析了中美场地土剪切波速转换关系，将从美国PEER地震记录数据库选取的220条地震记录按我国规范中的场地土类型进行分类，并以此作为地震输入.基于弹性SDOF体系简化三段式归一化等效速度谱，综合考虑刚度折减系数、延性系数和阻尼比对弹塑性SDOF体系等效速度谱的影响，采用归一化方法，提出了弹塑性SDOF体系归一化等效速度谱的确定方法.通过对参数进行多次拟合，定量给出弹塑性SDOF体系归一化等效速度谱的具体表达式及其参数取值，进而建议了一种适用于我国场地土类型，且便于实际应用的弹塑性SDOF体系归一化等效速度谱.

1　SDOF体系能量平衡方程及其求解

相对位移坐标系下，SDOF体系的振动微分方程为

将等式两边各项乘以相对位移微小增量dy=y·dt，并在0～t（t为地震持时内任一时刻）内积分，则

式（1）各项积分依次表示为

式中:We（t）为t时刻的动能；Wh（t）为t时刻的阻尼耗能；Wp（t）为t时刻的滞回耗能（包括弹性变形能和累计塑性变形能）；E（t）为t时刻的总输入能.参考文献［13］，任一时刻结构响应为

由式（4）可知，地震输入一定时，对于某一SDOF体系，位移、速度和加速度仅与结构的初始周期和阻尼比有关.结合式（3）可知，若不考虑结构滞回模型的影响，则地震输入一定时，SDOF体系地震输入能量仅与结构初始周期、质量和阻尼比有关.

为了消除质量影响，作者采用等效速度（Ve）来描述SDOF体系的地震输入能

2　地震动参数选取

2.1中美场地剪切波速转换

从PEER地震记录数据库［14］选取了220条地震记录进行统计分析.为使研究结果符合我国规范，将所选地震记录按中国场地土进行分类.美国规范以30 m深度处土层平均剪切波速vS30作为场地分类指标［14］，而我国规范则采用20 m深度处平均剪切波速vS20作为场地土划分标准［15］.参考吕红山等［16］和郭峰等［17］提供的中美剪切波速对应关系勘察资料，去除由于覆土层影响产生的偏离总体分布趋势的特殊点，分别计算出 vS20和 vS30的自然对数值.

以ln vS30为横坐标，ln vS20为纵坐标，对原有勘查数据进行拟合，见图1，进而建立ln vS30与ln vS20的关系式

式（6）拟合决定系数R2=0.937，可见，拟合效果较好，能够有效地实现中美场地剪切波速的转换.由式（6）得出vS30与我国场地土对应关系见表1，并以此作为后文选波依据.

表1　vS30与我国场地土类别对应关系Table 1　Correspondence between vS30and Chinese site classification

2.2地震记录选取

从PEER地震记录数据库［14］选取了220条地震记录，并按中国场地土类别将其分为5组，以每组44条记录作为地震输入，对SDOF体系地震输入能量谱进行统计分析.

表2给出了各条地震记录的详细参数:剪切波速vS30、峰值加速度aP、峰值速度vP、峰值位移sP、总持时Td和强震持时tD［18］.

表2　地震动参数Table 2　Ground motion parameters

2.3地面运动强度指标

地面运动强度越大，地震输入能量也越多.为了描述地面运动强度与弹性SDOF体系地震输入能量的关系，图2比较了6种复合强度指标（I1～I6）与220条地震记录时程分析得到的弹性SDOF体系等效速度谱峰值的线性相关性.以决定系数R2作为判定指标，建议采用Fajfar等［21］定义的复合强度指标I3表示阻尼比ξ=0.05的弹性SDOF体系等效速度谱峰值

3　阻尼比ξ=0.05的弹性SDOF体系归一化等效速度谱

图3采用时程分析法，分析阻尼比ξ=0.05，自振周期T为0.025～6 s（共240个点）的弹性SDOF体系等效速度谱，并按式（7）表示的谱峰值进行归一化，得到5类场地土条件下的归一化等效速度谱Vn，e.取均值加1.9倍标准差为代表值，以保证代表值曲线有90%以上保证率，得到阻尼比ξ=0.05的弹性SDOF体系归一化等效速度谱三段式曲线.

［9］和［24］，将阻尼比ξ=0.05的弹性SDOF体系归一化等效速度谱简化为

式中:Vn，e为对式（7）进行归一化的等效速度谱谱值；T1和T2分别为归一化等效速度谱平台段起始点，即简化三段式谱曲线初始周期分界点；Vn，e，max为归一化等效速度谱平台段谱值；a为下降段的衰减指数.经分段拟合，得到相关参数取值见表3.

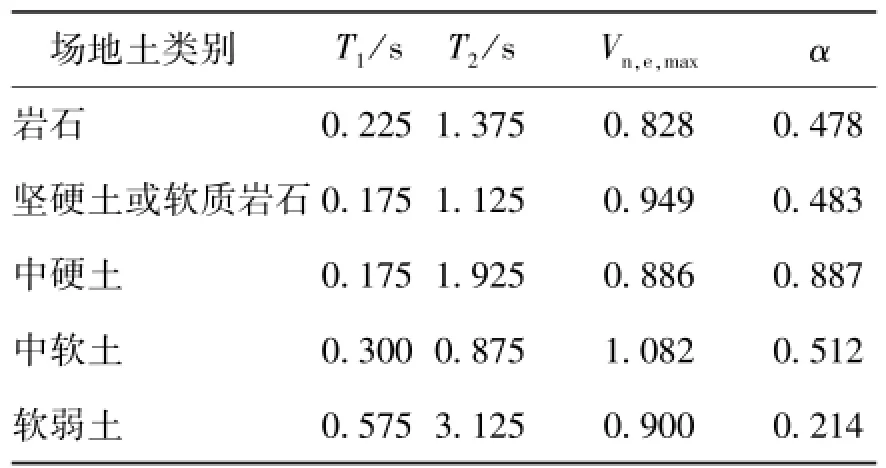
表3　弹性SDOF体系归一化等效速度谱相关参数Table 3　Related parameters of normalized equivalent velocity spectrum for elastic SDOF systems

4　结构参数对弹塑性归一化等效速度谱的影响

由于双线性弹塑性恢复力模型形式简单、计算方便，又能反映结构弹塑性滞回本质.因此，作者采用标准双线性滞回模型进行弹塑性计算，分析了结构滞回模型刚度折减系数、延性系数和阻尼比对弹塑性SDOF体系等效速度谱时程及峰值的影响.

4.1刚度折减系数的影响

取阻尼比ξ=0.05，延性系数μ=5，刚度折减系数α=0.05、0.06、0.07、0.08、0.09、0.10，从五类场地土中各取出1条地震记录作为输入，研究滞回模型刚度折减系数对弹塑性SDOF体系等效速度谱谱值Ve，p的影响.

重视对白粉病的防治。最佳防治时期在五叶期至抽薹，选用15%粉锈宁100 g兑水48 kg防治1-2次，提高千粒重。

图4给出了各类场地土条件下，不同刚度折减系数对应的弹塑性SDOF体系等效速度谱随初始周期的变化曲线.可见，滞回模型刚度折减系数对各类场地土弹塑性SDOF体系等效速度谱均无影响，故在下文讨论中未考虑刚度折减系数的影响.

4.2延性系数的影响

取阻尼比ξ=0.05，延性系数μ=1、2、3、4、5、6，从5类场地土中各取出1条地震记录作为输入，分析延性系数对弹塑性SDOF体系等效速度谱谱值Ve，p的影响.图5给出了各类场地土条件下，不同延性系数对应的弹塑性SDOF体系等效速度谱随初始周期的变化曲线.

由图5可知，同类场地土条件下，延性系数对弹塑性SDOF体系等效速度谱时程及峰值有明显影响.等效速度谱峰值和下降段衰减速度均随延性系数增大而减小，可见，延性系数增大对弹塑性SDOF体系等效速度谱峰值及下降段衰减速度有削弱作用.若适当调整延性系数，可改变弹塑性SDOF体系地震能量输入.

4.3阻尼比的影响

取阻尼比 ξ=0.02、0.05、0.10、0.15、0.20、0.30，延性系数μ=5，从5类场地土中各取出1条地震记录作为输入，分析阻尼比对弹塑性SDOF体系等效速度谱谱值Ve，p的影响.图6给出了各类场地土条件下，不同阻尼比对应的弹塑性SDOF体系等效速度谱随初始周期的变化曲线.

由图6可知，同类场地土条件下，阻尼比对弹塑性SDOF体系等效速度谱峰值有明显削弱作用；等效速度谱峰值和下降段衰减速度均随阻尼比增大而减小，但长周期范围内，等效速度谱时程却随阻尼比增大而增大.

5　弹性SDOF体系归一化等效速度谱的修正

由以上分析可知，不同场地土条件下，应综合考虑延性系数和阻尼比对弹塑性SDOF体系等效速度谱峰值及衰减段的影响.采用多次拟合方法，对弹性SDOF体系三段式简化等效速度谱的峰值及衰减段进行修正，并给出修正系数表达式及其参数取值，进而提出弹塑性SDOF体系地震输入等效速度谱的确定方法.

5.1峰值修正系数

以5类场地土条件下各44条地震记录作为输入，采用时程分析法，计算延性系数μ=1、2、3、4、5、6，阻尼比ξ=0.02、0.05、0.10、0.15、0.20、0.30的弹塑性SDOF体系等效速度谱峰值与阻尼比ξ= 0.05弹性SDOF体系等效速度谱峰值之比β（下文简称为相对峰值）.进而针对每类场地土，得出44条地震记录对应的β的平均值随延性系数和阻尼比的变化情况（见图7）.

先分别对5类场地土条件下，不同阻尼比对应的β随延性系数的变化进行三次函数拟合，再将系数对阻尼比进行二次拟合，最终将β表示成综合考虑阻尼比和延性系数的表达式为

式中a1、a2、a3、a4、a5、a6、a7、a8是与场地土类型相关的系数，其拟合值见表4.

5.2衰减段修正系数

以5类场地土条件下各44条地震记录作为输入，采用时程分析法，计算延性系数μ=1、2、3、4、5、6，阻尼比ξ=0.02、0.05、0.10、0.15、0.20、0.30的弹塑性SDOF体系等效速度谱下降段谱值与弹性SDOF体系下降段谱值之比γ（下文简称为相对谱值）.进而针对每类场地土，得出44条地震记录对应的γ的平均值随延性系数和阻尼比的变化情况.图8以岩石场地土条件为例，给出了不同延性系数对应的γ随初始周期和阻尼比的变化曲线.

通过多次拟合，分别将5类场地土对应的γ表示成自振周期、延性系数和阻尼比的表达式，进而对弹性SDOF体系归一化等效速度谱衰减段进行修正.5类场地土对应的γ可统一表示为

式中b1、b2、b3、b4、b5、b6、b7、b8是与场地土类型相关的系数，其拟合值见表5.

表4　β相关参数Table 4　Related parameters for β

表5　γ相关参数Table 5　Related parameters for γ

6　弹塑性SDOF体系归一化等效速度谱建立步骤

基于弹性SDOF体系简化三段式归一化等效速度谱，综合考虑延性系数、阻尼比、初始周期和场地土类型的影响，建议一种适用于我国场地土类型、可直接供设计使用的弹塑性SDOF体系三段式归一化等效速度谱，包括上升段、平台段和下降段3个阶段.具体确定步骤如下:

步骤1确定阻尼比ξ=0.02的弹性SDOF体系归一化等效速度谱.根据场地土类型，按式（8）和表3确定弹性SDOF体系按式（7）归一化后的等效速度谱，该谱值有90%的保证率.

步骤2峰值修正.综合考虑延性系数、阻尼比和场地土类型的影响，根据式（9）和表4，将阻尼比ξ=0.02的弹性SDOF体系峰值乘以修正系数β，确定弹塑性SDOF体系对式（7）表示的峰值归一化后的等效速度谱峰值.

步骤3衰减段修正.综合考虑延性系数、阻尼比、初始周期和场地土类型的影响，根据式（10）和表5，将阻尼比ξ=0.02的弹性SDOF体系衰减段表达式乘以修正系数 γ，确定弹塑性 SDOF体系对式（7）表示的峰值归一化后的等效速度谱衰减段曲线.

步骤4交点修正.若按上述步骤确定的弹塑性SDOF体系三段式简化谱曲线第1段终值和第3段起始值相差较大，则取两者平均值作为第1段终值、第2段平台段数值和第3段起始值，并将第1段和第3段谱值进行相应的比例缩放.最后，取3段交点为周期分界点.

7　本文所提出方法的验证

为验证本文所提出方法的有效性，图9以岩石（ξ=0.05，μ=2）、中硬土（ξ=0.1，μ=3）和中软土（ξ=0.2，μ=5）为例，分别将3类场地土条件下的44条地震记录作为输入，对弹塑性SDOF体系进行弹塑性时程分析，得到标准归一化等效速度谱曲线（对式表示的峰值进行归一）和代表值曲线（均值加1.9倍标准差）.将代表值曲线以弹性SDOF体系三段式简化谱曲线初始周期分界点为界，分3段进行拟合，与本文提出的基于弹性SDOF体系确定的弹塑性SDOF体系归一化等效速度谱曲线进行比较.

由图9可知，采用本文方法基于弹性谱计算的曲线和时程分析得到的拟合曲线整体走势一致，各周期分界点取值最大误差约为20%；上升段只在中软土（ξ=0.2，μ=5）情况下T=0处误差较大，但因实际中T≠0不存在，故不考虑此处误差；平台段和下降段基于弹性谱计算的曲线与拟合曲线取值最大误差分别约为5%和9%，在工程允许范围内；随着T的增大，下降段误差趋于稳定或逐渐减小.由此可见，采用本文方法确定的弹塑性SDOF体系归一化等效速度谱与时程分析结果吻合较好.

8　结论

1）弹性和弹塑性SDOF体系归一化等效速度谱均可简化为包含上升段、平台段和下降段的三段式曲线形式.

2）结构参数对弹塑性SDOF体系等效速度谱的影响为:滞回模型刚度折减系数无明显影响；延性系数和阻尼比增大均对等效速度谱峰值有消弱作用，但对谱曲线周期分界值无明显影响.

3）本文基于阻尼比ξ=0.02的弹性SDOF体系地震输入归一化等效速度谱，综合考虑刚度折减系数、延性系数、阻尼比、自振周期、场地土类型的影响，所建议的弹塑性SDOF体系地震输入归一化等效速度谱确定方法与弹塑性时程计算得到的拟合值吻合较好.

参考文献:

［1］魏新磊，周云，于敬海，等.基于结构能量分析的抗震设计新方法的研究［J］.世界地震工程，2003，19（3）:62-67.

WEI X L，ZHOU Y，YU J H，et al.Research on new methods of aseismic design of structures based on energy concept［J］.World Earthquake Engineering，2003，19（3）:62-67.（in Chinese）

［2］马千里.钢筋混凝土框架结构基于能量抗震设计方法研究［D］.北京:清华大学，2009.

MAQL.Studyonenergy-basedseismicdesign methodology and application for RC frames［D］.Beijing: Tsinghua University，2009.（in Chinese）

［3］HOUSNER G W.Limit design of structures to resist earthquakes［C］∥ ProceedingsoftheFirstWorld ConferenceonEarthquakeEngineering.Berkeley，California:Earthquake Engineering Research Institute，1956:1-12.

［4］HOUSNER G W.Behavior of structures during earthquake［J］.Journal of the Engineering Mechanics Division（ASCE），1959，85（4）:109-129.

［5］叶列平，缪志伟，程光煜，等.建筑结构基于能量抗震设计方法研究［J］.工程力学，2014，31（6）:1-12.

YE L P，MIU Z W，CHENG G Y，et al.Study on the energybased seismic design method of building structures［J］. Engineering Mechanics，2014，31（6）:1-12.（in Chinese）

［6］AKIYAMA H.Earthquake resistant limit state design for buildings［M］.Tokyo:University of Tokyo Press，1985: 23-30.

［7］肖明葵.基于性能的抗震结构位移及能量反应分析方法研究［D］.重庆:重庆大学，2004:24-35.

XIAO M K.Analysis method of displacement and energy responseforevaluatingtheperformanceofseismic structures［D］.Chongqing:Chongqing University，2004: 24-35.（in Chinese）

［8］刘哲锋，沈蒲生，胡习兵.地震总输入能量与瞬时输入能量谱的研究［J］.地震工程与工程振动，2006，26（6）:31-36.

LIU Z F，SHEN P S，HU X B.Study on input energy and momentary input energy spectra of earthquakestrong motion［J］.Earthquake Engineering and Engineering Vibration，2006，26（6）:31-36.（in Chinese）

［9］程光煜，叶列平.弹塑性SDOF系统的地震输入能量谱［J］.工程力学，2008，25（2）:28-39.

CHENG G Y，YE L P.Earthquake input energy sprctrum for inelastic SDOF systems［J］.Engineering Mechanics，2008，25（2）:28-39.（in Chinese）

［10］陈清军，袁伟泽.基于长周期地震动记录的SDOF体系能量谱探讨［J］.振动与冲击，2013，32（10）:36-42.

CHEN Q J，YUAN W Z.Energy spectrum of SDOF system based on long-period ground motion records［J］. Journal of Vibration and Shock，2013，32（10）:36-42.（in Chinese）

［11］周云，乐登，邓雪松.设计用地震动总输入能量谱研究［J］.工程抗震与加固改造，2008，30（5）:1-7.

ZHOU Y，YUE D，DENG X S.Research on input energy spectra for design of earthquake strong motion［J］. Earthquake Resistant Engineering and Retrofitting，2008，30（5）:1-7.（in Chinese）

［12］何利，叶献国.基于复合强度指标的弹塑性输入能量谱研究［J］.工程力学，2013，30（4）:7-14.

HE L，YE X G.Research on the elastic-plastic input energy spectrabasedoncompoundintensityindicator［J］. Engineering Mechanics，2013，30（4）:7-14.（in Chinese）

［13］包世华.结构动力学［M］.武汉:武汉理工大学出版社，2007:88-89.

［14］Pacific Earthquake Enginering Research Center.Peer strong motion database［DB/OL］.［2014-06-08］.http:∥peer.berkeley.edu/smcat/search.html.

［15］中国住房和城市建设部.建筑抗震设计规范:GB 50011—2010［S］.北京:中国建筑工业出版社，2010.

［16］吕红山，赵凤新.适用于中国场地分类的地震动反应谱放大系数［J］.地震学报，2007，29（1）:67-76.

LÜ H S，ZHAO F X.Site coefficients suitable to China site category［J］.Acta Seismologica Sinica，2007，29（1）:67-76.（in Chinese）

［17］郭锋，吴东明，许国富，等.中外抗震设计规范场地分类对应关系［J］.土木工程与管理学报，2011，28（2）:63-66.

GUO F，WU D M，XU G F，et al.Site classification corresponding relationship between Chinese and the overseas seismic design codes［J］.Journal of Civil Engineering and Management，2011，28（2）:63-66.（in Chinese）

［18］TRIFUNAC M D，BRADY A G.A study on the duration of strong earthquake ground motion［J］.Bulletin of the Seismological Society of America，1975，65（3）:581.

［19］ARIAS A.A measure of earthquake intensity［C］∥Seismic Design for Nuclear Power Plants.New York: Cambridge University Press，1970:438-483.

［20］HOUSNER G W.Measures of severity of earthquake ground shaking［C］∥Proceedings of the U.S.National Conference onEarthquakeEngineering.NewYork: University of California Press，1975:221-228.

［21］FAJFAR P，VIDIC T，FISCHINGER M.A measure of earthquake motion capacity to damage medium-period structures［J］.SoilDynamicsandEarth-quake Engineering，1990，9（5）:236-242.

［22］KRAMER S L.Geotechnical earthquake engineering［M］.Upper Saddle River，NJ:Prentice Hall，1996: 131-138.

［23］RIDDELL R，GARCIA J E.Hysteretic energy spectrum and damage control［J］.Earthquake Engineering& Structural Dynamics，2001，30:1791-1816.

［24］TENG J，DONG Z J.Research on energy spectrum of elastic SDOF［C］∥The 14th World Conference on Earthquake Engineering.Beijing:Science Press，2008: 195-196.

（责任编辑郑筱梅）

Earthquake Input Normalized Equivalent Velocity Spectrum for Inelastic SDOF Systems

TU Bingbing
（School of Science，Xi'an University of Science and Technology，Xi'an 710054，China）

Based on the relationship of shear wave velocity between the United States and China，220 seismic records were selected from American PEER database and classified according to Chinese site classification.With the normalized method，the equivalent velocity spectrum of elastic signle degree of freedom（SDOF）systems was simplified into three portions based on a complex intensity index.The influence of the SDOF system parameters on the earthquake input equivalent velocity spectrum for five types of site soil was analyzed.The results show that the stiffness deduction coefficient has no effect on the equivalent velocity spectrum，and the peak and the declining stage of the equivalent velocity spectrum decrease with the increase of ductility coefficient and damping ratio，respectively.With the multiple fitting methods，the modified coefficients for the peak and the declining stage of the normalized equivalent velocity spectrum for elastic SDOF systems were proposed by considering all influence factors.Finally，the normalized equivalent velocity spectrum for inelastic SDOF systems was suggested，and the effectiveness was verified.This method can be applied to Chinese site soil and is also convenient.

single degree of freedom（SDOF）systems；equivalent velocity spectrum；energy

TU 313

A

0254-0037（2016）06-0902-10

10.11936/bjutxb20155080052

2015-08-27

陕西省教育厅科学研究资助项目（15JK1478）；西安科技大学科研培育基金资助项目（201645）

屠冰冰（1986―），女，讲师，主要从事高层建筑结构抗震方面的研究，E-mail:tubingbing9@126.com