倒向随机微分方程在原保险定价中的应用

曹姗姗

(湖北师范大学 数学与统计学院，湖北 黄石　435002)



倒向随机微分方程在原保险定价中的应用

曹姗姗

(湖北师范大学 数学与统计学院，湖北 黄石435002)

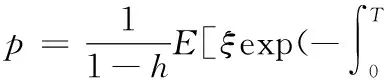
保险定价;倒向随机微分方程; “均值+方差”法;伊藤微分公式;Gisanov定理

保险定价是保险业务的关键内容，过高的保费能够让保险公司获得利益，但同时会使投保人望而却步，从而被市场淘汰出局；过低的保费会增加投保人的兴趣，但保险公司将承担更大的偿债风险，从而给予保险公司致命打击.所以说，合理的保险定价是保险公司生存与发展的关键因素. 现如今，保险业在飞速发展，各种保险品种不断涌现, 合理的定价是保险公司在市场中生存的关键，因而对保险定价的研究就更为迫切了.本文主要研究通常意义上的保险定价(原保险)，即保险人在平等自愿的基础上直接应投保人的要求而办理的保险业务的定价.

倒向随机微分方程(BSDE)的概念[1]是20世纪90年代初由我国数学家彭实戈和法国数学家Pardoux 引入的.之后其特殊的理论性质引起不少学者的关注，极大地推动了BSDE的发展.同时，许多金融数学家也把目光投向了BSDE在经济学领域上的研究，使得BSDE的应用性更加广阔和活跃.

1　保险定价的经典模型

在传统的保险定价中，概率和数理统计方法的研究已经拥有几百年的历史，各方面的有关文献也比较多. 实际应用中通常使用的定价法为“均值-方差法”，即“纯费率+附加费率”法[2].下面给出相关概念及计算公式：

1)保险费是投保人为转移风险，取得保险人在约定责任范围内所承担的赔偿(或给付)责任而交付的费用；保险金额是指保险人承担赔偿或者给付保险金责任的最高限额；保险费率，是应缴纳保险费与保险金额的比率,保险费率是保险人按单位保险金额向投保人收取保险费的标准，一般由纯费率和附加费率两部分组成.

4) 纯费率： Np=E(ξ)+mσ.其中 Np表示纯费率， E(ξ)表示平均损失率， σ 表示损失率的标准差， m表示倍数.

6)保险费率=纯费率+附加费率=(平均损失率+m倍标准差)+附加费率 ，其计算公式为：

p=E(ξ)+m σ+θ

2　 建立数学模型

在本节中，将借助于倒向随机微分理论，从而建立出原保险定价的数学模型.

引理1[3]伊藤微分公式：设 dxi(t)=bi(t)dt+ei(t)dwi(t)(i=1,2,3,…，n)函数G(x1,x2,…,xn,t)对t的一阶导数，对x的二阶导数关于x，t连续，其中x=(x1,x2,…,xn)∈Rn，t≥0，wi(t)(i=1,2,3,…,n) 是相互独立的维纳过程，则G(x1(t),x2(t),…,xn(t),t)满足如下随机微分方程：

其中G的下角标表示相对应变量的偏导数.

考虑连续市场情形，设(Ω,Ft≥0,F,P)为概率空间 (Ω,F,P)带σ代数流的概率空间，其中Ft≥0=σ(W(s)，0≤s≤t)即由标准布朗运动 {W(s),s≥0}产生的σ代数流.假设在金融市场中只有两种资产，其中一种为无风险资产，另一种为风险资产.假定x0(t) ,x1(t) 分别表示无风险资产的价格以及有风险资产的价格，x0(t) ，x1(t)∈R1满足下列方程：

(1)

其中，σ(t)>0表示风险资产波动率，r0(t) ，r1(t) 分别表示无风险资产收益率和风险资产预期收益率.

假设某种保险产品保险费用为 pQ，其中p 为保险产品价格(保险费率)， Q为投保者的保险额.设ξ 是随机变量，表示索赔率，则保险公司在t=T 时刻的赔偿为 ξQ.保险公司为能弥补损失将收取的保费进行风险投资，以获得足够回报.设公司的经营费用占保费的比例为h ，则保险公司可以用来投资的总费用为(1-h)pQ .在t=0 时刻，将(1-h)pQ 投资于风险市场，总资产将随时间的变化而变化.记总资产为y(t) ，则y(0)=(1-h)pQ .保险公司在风险市场中投资是为了使 y(T)>ξ Q，但因为假设的金融市场为无套利市场，所以有公平价格，使得关系式y(T)=ξ Q成立.

对(1-h)pQ 进行风险投资组合，即将其分为两部分，设风险资产占有百分率为u(t),u(t)∈[0,1] ，无风险资产占有 1-u(t).则投资于风险资产和无风险资产的费用分别为y(t)u(t)=(1-h)pQu(t) ，y(t)[1-u(t)]=(1-h)[1-u(t)]pQu(t) .由伊藤微分公式，对(1)式进行计算，可得总资产y(t) 满足下列倒向随机微分方程：

令z(t)= σu(t)y(t)，则上述方程可转换为

(2)

在总资产y(t) 满足倒向随机微分方程(2)的基础上,找到保险的公平价格p ,从而满足y(0)=(1-h)pQ .

3　原保险定价公式的推导

dy(t)=a(s,w)dt+dWt,t≤T,y0=0

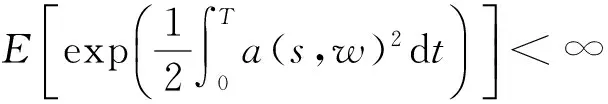
定理假设保险公司是风险中性的，其资产y(t) 满足倒向随机微分方程(2)，则保险定价为：

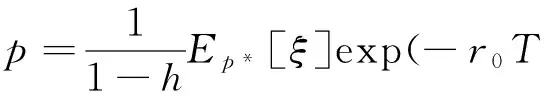
证明为证得结论首先需引入概率测度P*,令

则P*为P的等价概率测度.又由引理2可知随机过程

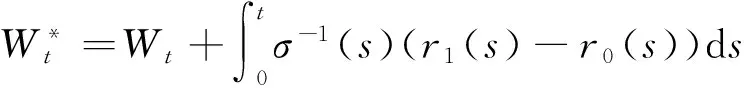
(3)

下求方程(3)的解.

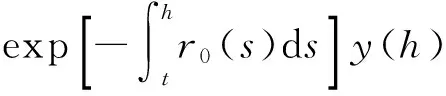
对如上等式两边从t 到T 积分得：

对上式两边取EP*[*|Ft] ，得EP*[Is|Ft] =0.

本小节得出的定价公式显示，保险价格(保险费率)只与平均索赔率(损失率)和无风险收益率有关,这使得保险费率的变化不会太大，比较符合实际情况.

4　算例分析

因保险公司相关数据都为商业机密不对外公开，所以较难获取实际数据，因此假设设无风险收益率 r0=6%，T=1 , h=10%，附加保费为1‰ ，有表1:

表1　全国意外险业务历年赔款额和保险金额的数据

i)“均值-方差”法

再根据保险费率计算公式可得：

p=E(ξ)+mσ+θ=3.56‰+0.2‰+1‰=3.86‰

ii)根据本文得出的保险定价公式有：

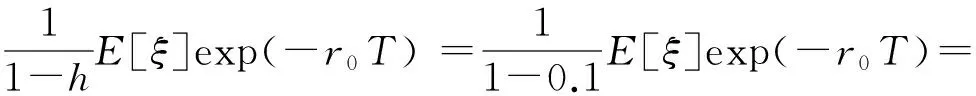
虽然假设数据不是特别准确，但是通过上述两种方法的求值比较，说明保险定价公式有一定的可行性的.这也说明倒向随机微分方程在保险定价问题的应用上具有广阔前景的.

[1]Pardoux E,Peng S.Adapted solution of a backward stochastic differential equations [J]. Systems Control Letters,1990,14:55～61.

[2]孙国忠,王秀莲.基于风险投资理论的保险定价研究[J].工业技术经济，2005,137：88～89.

[3]陈佳.倒向随机微分方程在保险业定价问题中的应用[D].北京：北方工业大学，2007.

[4]彭实戈.倒向随机微分方程及其应用[J].数学进展,1997,26(2):97～112.

[5]黄志远.随机分析学基础[M].科学出版社,1998.

[6]程中华,宁伟.倒向随机微分方程在保险定价中的应用[J].经济研究，2010，9：74～75.

Application of backward stochastic differential equations in the pricing of original insurance

CAO Shan-shan

(College of Mathematics and Statistics, Hubei Normal University, Huangshi435002 , China)

In this paper, assuming that there are only two assets (no risk asset and risk assets) in the financial , we establish pricing model of original insurance price by using the backward stochastic differential equation , then work out the solution of equation to get the pricing formula . And test the feasibility of the pricing formula through the contrast of "mean-variance" pricing.

insurance pricing; BSDE ; "mean-variance" method; differential equation; Gisanov theorem

2016—01—25

曹姗姗(1990—)，女，湖北大冶人，硕士研究生，主要研究方向为倒向随机微分方程及其应用.

F832.p

A

1009-2714(2016)02- 0060- 04

10.3969/j.issn.1009-2714.2016.02.013