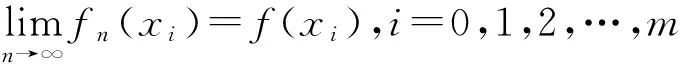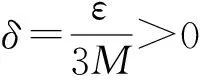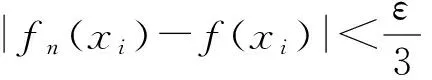函数序列一致收敛性的分析与证明

严　慧

(湖北师范大学 数学与统计学院，湖北 黄石　435002)



函数序列一致收敛性的分析与证明

严慧

(湖北师范大学 数学与统计学院，湖北 黄石435002)

函数序列一致收敛性是数学专业微积分理论特有的教学内容，既是重点也是难点，着重围绕着“有限支点法”，对一致收敛性证明中常用的工具：有限覆盖定理，致密性原理，单调性，一致连续性，李普希兹条件的应用技巧进行了分析与探讨.

函数序列；一致收敛；有限覆盖定理；致密性原理

极限理论是微积分学的理论基础，是大学数学教育课程“高等数学”和“数学分析”中最重要的内容.而这两门课程的根本区别在于：是否包含“一致极限”理论. 非数学专业开设的“微积分”或“高等数学”中不包含这部分内容.而数学专业开设的微积分学课程“数学分析”则将“一致极限理论”作为其重要的教学内容. 这从一个侧面反映了这部分内容的理论深度和难度. 但它却又是进行数学研究必不可缺的基本工具.特别是函数序列的一致收敛性理论，因为在数学研究的实际工作中，极限问题经常是与某些参数有关的.因而一致收敛性理论已成为数学专业研究生入学考试的热门课题，也是数学专业学生必需掌握的内容，但这方面的专题讨论尚少.

本文中，我们将对函数序列一致收敛性理论与方法作一系统的分析和讨论，重点放在一致收敛性问题证明方法的综述上，我们介绍了有限覆盖定理，致密性原理，单调性条件一致连续性， 李普希兹条件等在函数序列一致收敛性讨论中的应用.

1　一致收敛性的概念与常用方法

设 {fn(x),n≥1}是X上的函数序列，普通的收敛性fn(x)→f(x)(n→∞)是指:对任意的ε>0，存在N(ε，x)>0,当n>N时|fn(x)-f(x)|<ε.

而序列{fn(x),n≥1}在X上一致收敛于f(x)(n→∞)是指对:任意的ε>0，存在仅依赖于ε的N(ε)>0，当n>N时,对 ∀x∈X均有 |fn(x)-f(x)|<ε.

相对于后一种收敛性，我们常称前一种收敛为“点点收敛”或“逐点收敛”.因为对于每一个x∈X，(相对于极限中的变量n，我们称之为参变量)，fn(x)相当于普通的数列，因而其收敛性也即普通数列的收敛，但因不同的x就是不同数列，因此这里极限定义中的N随x变化而变化，并没有一个共同的N，这种极限我们称之为局部极限.

而一致收敛性中的N是对所有x∈X都适用的.这是把函数fn(x)视为一个整体的收敛性,这种收敛我们也称为整体收敛或全局收敛.

如果参变量集X 是有限集合，显然逐点收敛和一致收敛并无区别，因此一致收敛性问题中的参变量总假定是无限集，而此时这二种收敛性则完全不同了，因为无限集未必有最大或最小元.函数列的一致收敛性首先要求逐点收敛，但这仅是一种局部性质，要完成局部性质向整体性质的转变必需要有一定的条件和适当的工具.下面我们将介绍几个常用的工具，而基本思路我们将其称为“有限支点法”，利用有限个支点托起整个参变量集合.

首先考虑有限覆盖定理的应用.

有限覆盖定理：若闭区间[a,b] 存在开覆盖则 [a,b]必存在有限子覆盖.

有限覆盖定理所起的作用是明显的，因为它实现了从无限(开覆盖)到有限(子覆盖)的转化，而有限性等同于一致性.这一工具使用的要点在于“覆盖”(邻域)的构造．

例1(狄尼定理)若有限闭区间 [a,b]上连续函数序列 {sn(x)}收敛于连续函数s(x) ，且对∀x∈[a,b] ，sn(x) 关于n单调，则序列在 [a,b]上一致收敛于s(x) (n→∞).

分析与证明 使用有限覆盖定理的要点在于利用局部性质构造具有某种性质的邻域(开覆盖)

不妨设sn(x)↑s(x) (n→∞),否则可用-sn(x) 代替．

首先考虑局部性质，即逐点收敛性：对 ∀x∈[a,b] ，由于sn(x) ↑s(x) (n→∞)，故对 ∀ε>0 ，∃Nx,当n≥Nx时

0≤s(x)-sn(x)≤s(x)-sNx(x)<ε

(1)

由于sNx(y) 及s(y) 在 [a,b]上连续，故存在ηx>0,使当y∈U(x,ηx):=(x-ηx,x+ηx)⊂[a,b]时

|SNx(y)-SNx(x) <ε,|s(y)-s(x)| <ε

(2)

于是我们证明了对于每个x，存在邻域U(x,ηx) ，当y∈U(x,ηx)时，(2)成立，此时，我们完成了局部性工作，即覆盖(邻域)的构造．

利用有限覆盖定理，即可完成从局部到整体的转化．

0 ≤s(x)-sn(x)≤s(x)-sN(x)≤s(x)-SNxi(x)=

[s(x)-s(xi)]+[s(xi)-SNxi(xi)]+[SNxi(xi)-SNxi(x)]

对第一、第三个中括号使用(2)，第二个中括号使用(1)即得：当n>N时，

s(x)-sn(x)<ε+ε+ε=3ε对 ∀x∈[a,b]成立．

即序列{sn(x),n≥1}在 X上一致收敛于s(x) (n→∞)．

我们称上述方法为“有限支点法”，这是本文着重介绍的方法，例1中我们通过有限覆盖定理构造有限支点x1,x2,…,xm，通过这些支点的邻域托起整个参变量集[a,b] .

下面的例2中我们将通过“一致连续性”+“单调性”构造有限支点集．

例2设函数列{fn(x),n≥1}在 [a,b]上收敛于连续函数f(x)，若对每个n，fn(x) 在 [a,b]上单调，则fn(x)在 [a,b]上一致收敛于f(x) ．

分析与证明 设fn(x)关于x∈[a,b]，显然f(x)在闭区间[a,b] 上一致连续，一致连续性是函数的一个整体性质，利用此整体性质分割[a,b] 是构造“有限支点集”较为简便的方法．

事实上，由f(x) 在[a,b] 上一致连续，对任意的ε>0,存在δ>0，使:

当x,y∈[a,b],|x-y|<δ时

|f(x)-f(y)| <ε

(3)

用步长δ分割 [a,b]：a=x0

|fn(xi)-f(xi)| <ε,i=0,1,…,m

(4)

设x∈[a,b]，则存在i，使x∈[xi,xi+1]，fn(x) 关于x↑，于是当n≥N时，由(3)(4)

fn(x)-f(x)≤fn(xi+1)-f(x)=[fn(xi+1)-f(xi+1)]+[f(xi+1)-f(x)]<ε+ε=2ε

fn(x)-f(x)≥fn(xi)-f(x)=[fn(xi)-f(xi)]+[f(xi)-f(x)] >-ε-ε=-2ε

即

|fn(x)-f(x)|< 2εx∈[a,b]

下面的例3利用李普希兹条件构造“有限支点集”．

例3设函数列 {fn(x),n≥1}在 [a,b] 上有意义，且满足如下李普希兹条件，对所有n和x,x' ∈[a,b]，下式成立

|fn(x)-fn(x')|≤M|x-x'|

(5)

其中M为与n无关的常数．

若对x∈[a,b]

(6)

则{fn(x) }在 [a,b] 上一致收敛于f(x) .

(7)

令n→∞，得

现有研究中，针对社会化信任关系的协同过滤技术的隐私保护工作尚不多见.因此，从考虑隐私保护和预测准确率两者间的折中以及协同过滤技术中的数据稀疏性和冷启动问题，本文将差分隐私保护技术引入融合显/隐式信任关系的SVD++协同过滤技术中，提出目标函数加扰的TrustSVD差分隐私保护新策略.关于新策略，文中在理论上分析了其隐私保护的性能，实验上验证了其在协同过滤应用中的预测表现.结果表明：所提新策略与无隐私保护的TrustSVD具有相近的预测准确率，与做类似差分隐私保护的SVD++相比获得了更优的预测结果，此外还给出了核心参数的调节实验.

(8)

以步长δ分割 [a,b]，a=x0

(9)

对x∈[a,b] ，设x∈[xi,xi+1] ，当n>N时，由(7)(8)(9)

{fn(x),n}在 [a,b]上一致收敛于f(x)(n→∞).

上面各个例子中的闭区间都可改为更一般的紧集。利用紧集的致密性原理也是证明函数序列一致收敛的常用方法，基本思路是假设不一致收敛，构造出序列 {xn:n≥1}，对其使用致密性原理推出矛盾，在教学中，这种反证法也许学生更容易掌握．

例4同例1狄尼定理，但使用致密性原理证明．

反证 若{Sn(x),n≥1} 不一致收敛到s(x)(n→∞) ，则存在ε0>0，对任意N，存在n1>N，及x1∈[a,b] 使

|Sn1(x1)-s(x1)| ≥ε0

(10)

递推地，按此可取到正整数n1,n2,… 和 [a,b] 中的点x1,x2,… 使

|Snk(xk)-s(xk)| ≥ε0n1

(11)

由{xk:k≥1}⊂[a,b]，及致密性原理，存在子列不仿仍记为 {xk:k≥1} ,使

xk→ξ∈[a,b](k→∞)

(12)

因sn(ξ) →s(ξ)(n→∞) ，故对任意ε>0，存在N使|SN(ξ) →s(ξ)|<ε.

注意到SN(x)-s(x) 在ξ处连续及xk→ξ(k→∞) 得

(13)

故存在K，当k>K时

|SN(xk)-S(xk)<ε

固定xk,sn(xk)对n单调，故当k>K,n>N时

|Sn(xk)-s(xk)|≤|SN(xk)-S(xk)|<ε

由ε的任意性，此与(10)矛盾，故必有 {SN(x):n≥1}在[a,b] 上一致收敛到s(x) .

(14)

命题获证．

[1]陈传章，金福临，朱学炎，等.数学分析(第二版)[M].北京：高等教育出版社，1983.

[2]华东师范大学数学系.数学分析(上、下册)(第四版)[M].北京：高等教育出版社，2010.

[3]钱吉林.数学分析题解精粹(第二版)[M].武汉:崇文书局，2003.

[4]胡适耕,姚云飞.数学分析——定理·问题·方法[M].北京:科学出版社，2007.

Analysis and proof methods of convergence uniform for functions sequence

YAN Hui

(Collage of Mathematics and Statistics, Hubei Normal University, Huangshi435002,China)

The convergence uniform for functions sequence is the peculiar content of the calculus for the students of mathematics specialty. It is both the key point also is the difficult point. In this paper, we mainly consider the finite supporting point methods and discuss the applications of the theorem of finite covering, accumulation principle, monotonicity, uniform continuity and Lipschitz condition.

function sequence; convergence uniform; theorem of finite covering; accumulation principle

2015—12—28

严慧(1983—)，女，湖北黄梅人，硕士，讲师，主要从事概率论与数理统计研究.

O172.2

A

1009-2714(2016)02- 0115- 04

10.3969/j.issn.1009-2714.2016.02.025