基于多策略离散粒子群算法的MPRM电路延时与面积优化

符　强，汪鹏君，童　楠，王铭波，张会红

(1.宁波大学电路与系统研究所，浙江宁波 315211； 2.宁波大学科学技术学院，浙江宁波 315212)



基于多策略离散粒子群算法的MPRM电路延时与面积优化

符强1,2，汪鹏君1，童楠2，王铭波2，张会红1

(1.宁波大学电路与系统研究所，浙江宁波 315211； 2.宁波大学科学技术学院，浙江宁波 315212)

针对大规模混合极性Reed-Muller(Mixed Polarity Reed-Muller,MPRM)逻辑电路的延时与面积优化，提出一种基于多策略离散粒子群优化(Multi-Strategy Discrete Particle Swarm Optimization,MSDPSO)的极性搜索方法.在MSDPSO算法中，对粒子进行团队划分，每个团队既执行不同策略，又相互联系，并行完成探索与开发的双重任务.同时在进化过程中采用高斯调整来激活寻优能力较差的粒子.结合MSDPSO算法和列表极性转换技术，对大规模MPRM电路进行延时与面积极性搜索.最后对PLA格式的MCNC Benchmark电路进行算法性能测试，结果验证了MSDPSO算法的有效性.与离散粒子群优化(Discrete Particle Swarm Optimization,DPSO)算法的优化结果相比较，MSDPSO算法获取的电路延时平均缩短8.43%，面积平均节省38.36%.

多策略离散粒子群算法；MPRM逻辑电路；延时与面积优化；极性搜索

1　引言

任意逻辑函数的表达和实现都具有布尔逻辑形式和Reed-Muller(RM)逻辑形式.基于XOR/AND 或XNOR/OR运算的RM逻辑在算术电路、奇偶校验电路及通信电路等应用中，具有比布尔逻辑更紧凑的结构和更好的可测性.随着电子行业对环保节能要求的不断提高，RM逻辑设计因其特有优势越来越受到学术界关注.其中，RM逻辑电路的延时与面积优化是电路综合和优化技术的重要组成部分，受到了普遍重视.

常用的RM逻辑主要有固定极性RM(Fixed Polarity Reed-Muller,FPRM)和混合极性RM(Mixed Polarity Reed-Muller,MPRM)两种展开式.对于n个输入变量的逻辑函数，有2n个固定极性及3n个混合极性，分别对应着2n种FPRM展开式及3n种MPRM展开式.MPRM表达式包含所有FPRM表达式，因此能够获取更优的电路结构.

不同的电路极性对应于不同的电路逻辑展开式，相应的电路延迟和面积大小也不一样.因此，只有确定较佳的电路极性，才能优化MPRM电路的延时和面积[1].MPRM电路极性搜索实质是一个组合优化问题，对于变量数较少的电路，可以通过枚举法来实现最优极性的搜索，但是随着电路规模的增大，枚举法在有限时间内完成最优极性搜寻任务将变得愈发困难，需要快速有效的优化算法来搜索电路最佳极性.

群体智能算法，如离散粒子群优化算法[2](DPSO)、遗传算法[3](Genetic Algorithm，GA)及蚁群算法[4](Ant Colony Algorithm，ACA)等是近年发展起来的新型优化方法，在快速解决大型复杂组合优化问题时具有一定优势，已得到广泛应用.在MPRM电路优化设计领域，近年来也出现了关于群体智能算法的应用研究，并取得一定的成果.如文献[5]在遗传算法中引入粒子群算法的搜索机制，提出了一种能有效提高电路面积优化效果的方法；文献[6]基于多种群协同思想，并结合三种不同的变异更新方法提出了一种混合多值离散粒子群优化算法，加快了电路极性优化的速度.

与其他同类算法相比，模拟鸟群觅食的DPSO算法结构简单、易于编程，同时具有搜索速度快、通用性强等优点.在线性减小的惯性权重作用下，DPSO算法中的粒子记录自身最优值，并追随种群最优个体进行先全局探索后局部开发的寻优策略，能够迅速定位并捕捉目标.但是在算法运行后期，粒子将集聚在局部最优区域，易于发生早熟状况.

鉴于此，针对大规模MPRM电路的特点，提出一种基于多策略离散粒子群算法(MSDPSO)的MPRM电路延时与面积优化方法，将决定MPRM电路延时与面积的电路极性表示为算法中的粒子，并利用列表技术进行极性转换.然后通过粒子种群的迭代进化搜索到MPRM电路的最佳极性，优化电路延时与面积设计.最后将对大规模的MCNC Benchmark电路进行测试以验证算法的有效性.

2　极性转换与延时和面积估计模型

2.1极性转换

在MPRM电路中，逻辑函数f(xn-1,xn-2,…,x0)有3n个混合极性，其中极性p的MPRM展开式可表示为：

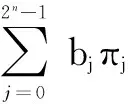
(1)

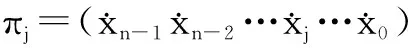
(2)

(3)

(4)

在MPRM展开式的极性转换算法中，列表转换技术[7]能实现任意输入变量逻辑函数的快速转换，是应用最广泛的转换算法之一.基于列表转换技术的从混合极性p转换到极性q的算法描述如下所示.

2.2延时和面积模型构建

2.2.1逻辑分解

对MPRM电路进行逻辑分解能有效简化电路，利于延迟优化.常用的逻辑分解方法是对逻辑电路表达式进行提取公因式操作，从而不断简化电路结构.根据Ashenhurst算法[8]，MPRM展开式的具体逻辑分解形式如式(5)所示：

f(xn-1,xn-2,…,x0)=f(A)·f(B)

(5)

其中，A={xn-1,xn-2,…,xi}和B={xi-1,xi-2,…,x0}.符号“·”为与运算.

因此，MPRM电路展开式的逻辑分解算法描述如下：

2.2.2延时和面积估计模型

在数字逻辑设计中，产生延时的主要因素是逻辑门的传输延迟，电容及其他因素可以忽略.将二输入门的传输延时大小定义为一个单位时间，则可先分解电路为二输入AND门和二输入XOR门组合，然后进行延时与面积计算.设N(U)为二输入门电路网络，将N中的节点总数目表示电路面积，而电路延迟可记为二输入门在关键路径的传输延时之和.j为节点集合U中的某一节点，代表一个二输入门，其延迟可表示为[9]：

tj=1+max(tj-a,tj-b)

(6)

其中，tj-a和tj-b为节点j的输入延迟，tj为节点j的输出延迟，j∈U.

类Huffman算法常用于获取逻辑电路的最小延迟.设T=T1·T2·…·Ti·…Tc为一个MPRM展开式，其中Ti为第i个向量的子展开式，c为逻辑分解后的终端节点向量个数.令原始输入信号的延时为0，则MPRM电路的延迟分解算法可以描述为：

3　多策略离散粒子群算法(MSDPSO)

3.1离散粒子群算法(DPSO)

在DPSO算法中，每个个体的位置和速度都以随机方式在解空间内进行初始化.假设粒子种群中的粒子总数为m，搜索空间为n维，其中第i个粒子在n维空间的位置可表示为Xi=(xi0,xi1,…,xij,…,xin-1)，其飞行速度可表示为Vi=(vi0,vi1,…,vij,…,vin-1).记个体最优位置pbesti=(pbesti0,pbesti1,…,pbestij,…,pbestin-1)，粒子群最优位置gbest=(gbest0,gbest1,…,gbestj,…,gbestn-1).则个体速度更新分别如式(7)和式(8)所示：vij(t+1)=w(t)·vij(t)+c1·random1()·(pbestij-xij(t))+c2·random2()·(gbestj-xij(t))

(7)

xij(t+1)=round(M/(1+exp(-vij(t+1)))+(M-1)

·k·random3())

(8)

其中：t为当前进化代数；random1()，random2()和random3()是(0,1)范围内的随机数；round为取整操作；1+exp(-vij(t+1))为sigmoid函数；M是xij的取值状态数量，k是一常数；c1和c2为加速因子，用于调整粒子向pbest和gbest转移的速度；w是惯性权重，用于协调粒子群体的开发与探索能力.

3.2多策略离散粒子群算法(MSDPSO)

在DPSO算法中，由于gbest粒子对其他粒子的牵引作用过强，容易引导所有粒子迅速收拢，形成了种群的快速趋同效应，导致算法陷入局部最优解.针对以上缺点，文献[10]借鉴遗传算法机制，提出了一种改进型DPSO算法(HDPSO)，该算法在粒子群体陷入早熟状态时，利用精英策略及变异算子以帮助粒子跳出局部最优区域，在一定程度上优化了粒子种群的搜索性能.

近年来，群体智能优化方案中的多策略集成设计研究越来越得到关注[11,12].多策略集成思想指出，由于所求问题的特征不同，单一的搜索策略不易满足各类要求，因此智能群体在寻优过程中应提供多种搜索策略，并通过策略整合来平衡探索和开发的双重要求.鉴于此，提出了一种基于多策略的离散粒子群算法，通过组建具有不同寻优策略的粒子团队，设置相应的策略集成方案，来实现探索和开发的并行操作.

3.2.1多策略划分

将种群中的粒子按比例分为执行不同策略行为的两个团队：senior team和junior team.其中senior team执行开发活动，而junior team承担探索任务.具体策略划分方案如下：

对于senior team中的个体，其主要任务为快速高效地进行局部开发.令senior team中的粒子围绕着种群最优个体，按照式(7)和式(8)搜索当前最优区域中的最优解.为了进一步提高寻优效率，该队所有粒子在完成跟随行为后，将再次以高斯搜索模式进行一次随机游走，寻找自身当前位置附近可能存在的更好值.此时速度更新公式调整为式(9)：

vij(t+1)=c3*gaussian

(9)

其中，gaussian为服从均值为0，方差为1的随机数；c3为一常数.

对于juniorteam中的个体，其主要任务为扩展粒子视野，增加粒子行为多样性.设置juniorteam中的粒子在每一次迭代进化中以概率ρ靠近在seniorteam中随机选择的某个粒子，而以1-ρ的概率执行相反操作.因此，juniorteam中粒子的速度更新公式可由式(10)表示：

vid(t+1)=sgn(random4()-(1-ρ))·(w(t)·vij(t)

+c1·random1()·(pbestij-xij(t))

+c2·random2()·(Xsij(t)-xij(t)))

(10)

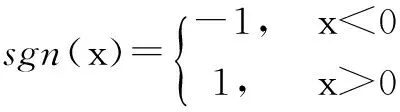
junior team中的个体不是追踪gbest，而是以senior team为跟踪目标，扩大了吸引子的范围，因此个体视野更为广阔.同时，junior team中的个体在一定概率下也存在反向跟踪的可能，增强了全局探索行为，预防过多个体陷入同一局部区域.

3.2.2多策略集成

senior team负责快速锁定局部搜索目标，而junior team强调保持种群多样性，扩大搜索区域.两个团队内的粒子执行不同的学习策略，具有不同的搜索进化能力，在种群内部构建探索与开发的并行优化方案，增加全面寻优的可能性.当所有粒子完成一轮寻优后，为进一步提高种群整体搜索性能，将粒子按照适应度大小进行排序，并将最差的10%个体进行速度高斯调整(速度更新公式如式(9)所示)，以激活种群该部分粒子的寻优能力.

4　基于MSDPSO的MPRM电路最佳延时和面积极性搜索

在求解MPRM电路延时和面积优化问题时，MSDPSO中的搜索空间维度D对应于MPRM电路的变量数.粒子位置对应于电路的极性，即电路极性可以表示为xi=(xi0,xi1,…,xiD-1)，xij的取值范围为xij∈{0,1,2}，因此式(8)中的M=3.MSDPSO中的最优粒子位置gbest则表示MPRM电路优化搜索中的最佳极性.

4.1粒子更新及域约束

对于seniorteam中的粒子，按照式(7)、式(8)、式(9)进行速度及位置更新；对于juniorteam中的粒子按照式(8)、式(10)进行更新操作.

为了防止粒子由于飞行过快而失去控制，应对其速度进行约束，如式(11)所示：

(11)

同时限制粒子在合理区间内飞行，由于xij∈{0,1,2}，

于是可得位置约束表达式如下所示：

(12)

4.2适应度函数

MPRM电路的极性优劣决定其延时和面积的大小，某一极性越好，则说明该极性对应电路的延时与面积越小.因此MSDPSO算法需要对每个极性进行评价，以确定最优极性值.结合延时与面积的优化要求，适应度函数可表示为：

fitness(xi)=α·area(xi)/total-area

+(1-α)·delay(xi)/total-delay

(13)其中，area(xi)和total-area分别为是第i个粒子对应的MPRM电路面积及所有粒子对应的面积之和.delay(xi)和total-delay分别为是第i个粒子对应的电路延时和所有粒子对应的延时之和.α是优化权重系数，其取值范围为[0,1].

4.3最佳极性搜索

综合以上对MPRM电路延时和面积模型的分析，以及对MSDPSO算法的设计，提出针对MPRM电路延时和面积最优化要求的MSDPSO极性搜索方案如下：

5　实验与分析

为验证MSDPSO算法在求解MPRM电路的面积和延时的有效性，将MSDPSO算法与DPSO算法和文献[10]中的混合粒子群算法(Hybrid Discrete Particle Swarm Optimization，HDPSO)进行了性能对比.三种算法均用c++语言实现，并在Windows XP操作系统下，通过VC6.0编译，程序的硬件环境为Inter Pentium CPU G645(2.9GHz)1.82GB RAM.测试电路采用PLA格式的MCNC Benchmark电路.

在测试实验中，MSDPSO算法的参数设置为：优化权重α=0.5，加速因子c1=c2=1.5，粒子总数Population=40，迭代进化次数iteration=120，c3=0.3.seniorgroup与juniorgroup的粒子数比例为8∶2，惯性权重w的最小值wmin=0.4，wmax=0.9，vmax=4，参数k=0.2，ρ=0.2.DPSO算法与HDPSO算法的参数设置与文献[10]相同.选用15个中大规模的Benchmark电路[10]分别进行了算法测试，为减小随机数影响，将所选的电路通过三种算法分别测试5次，并将5次优化结果之和作为最终测试结果.MSDPSO、DPSO、HDPSO算法各自取得最佳极性对应的延时与面积结果如表1所示.

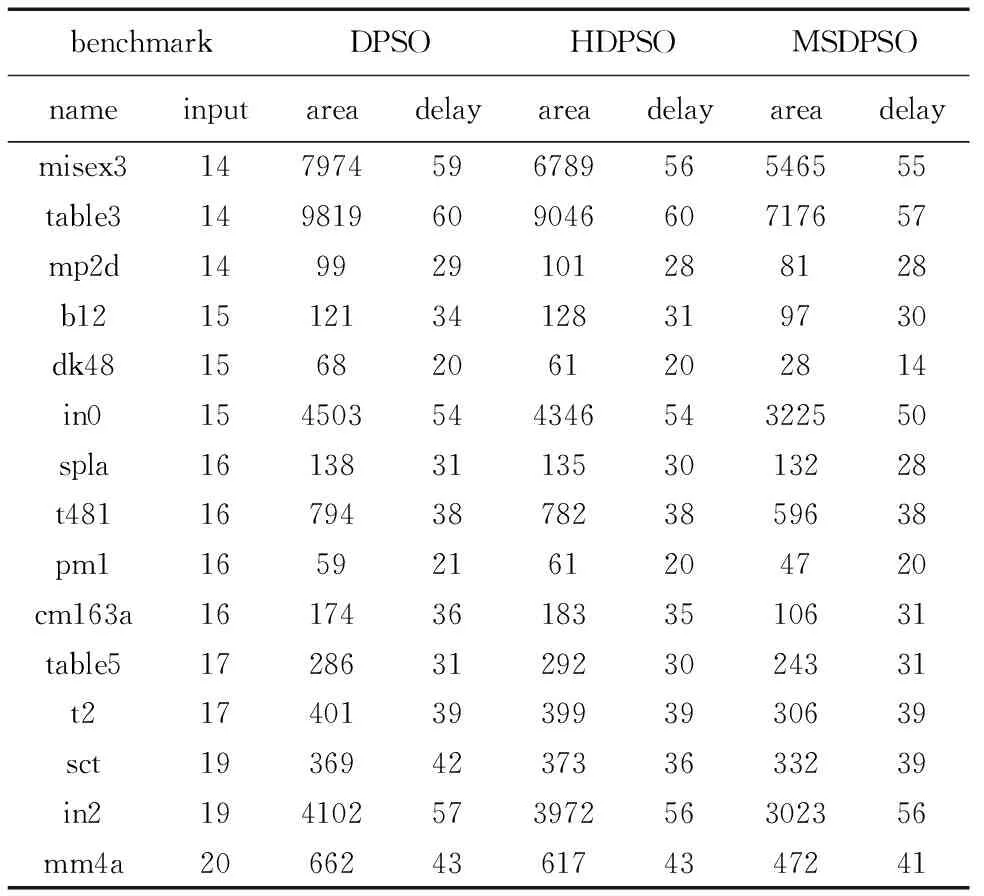
表1　MSDPSO与其他算法最佳极性对应的延时与面积

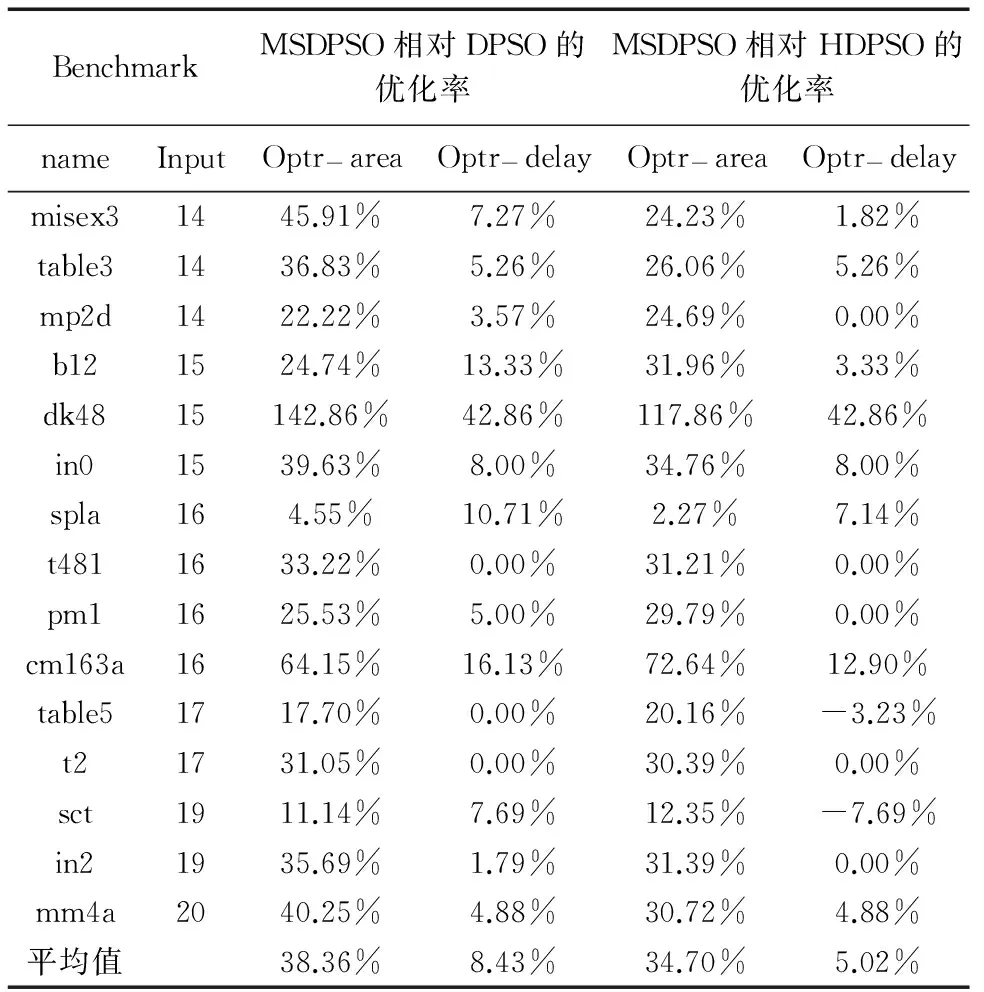
表2　MSDPSO算法相对其他算法的优化率

表2为MSDPSO算法相对DPSO算法及HDPSO算法的优化率，其中，优化率Optr-area、Optr-delay的计算公式为：

Optr-area=(OA1(OA2)-OA3)/OA3

(14)

Optr-delay=(OD1(OD2)-OD3)/OD3

(15)

其中，OA1、OA2、OA3分别为DPSO、HDPSO、MSDPSO算法搜索到的面积最优解；OD1、OD2、OD3分别为DPSO、HDPSO、MSDPSO算法搜索到的延时最优解.

从表1、2的测试数据看出，与DPSO算法及HDPSO算法相比，MSDPSO算法能获取更小的电路面积和更短的电路延时.如dk48电路，MSDPSO算法相比其他算法的面积优化率分别达到142.86%和117.86%，延时优化率均为42.86%.虽然在table5及sct测试中，MSDPSO算法比HDPSO算法在延时方面有所延长，但同时在面积方面获得了更多优化.就整体测试结果而言，MSDPSO算法相比DPSO算法，平均面积优化率为38.36%，平均延时优化率为8.43%；与HDPSO算法相比，MSDPSO算法的平均面积减小了34.70%，平均延时缩短了5.02%.

为了更好地观察MSDPSO算法的搜索性能表现，本文将MSDPSO、DPSO和HDPSO三种算法的面积与延时迭代进化过程进行比较分析，结果如图1、图2所示.

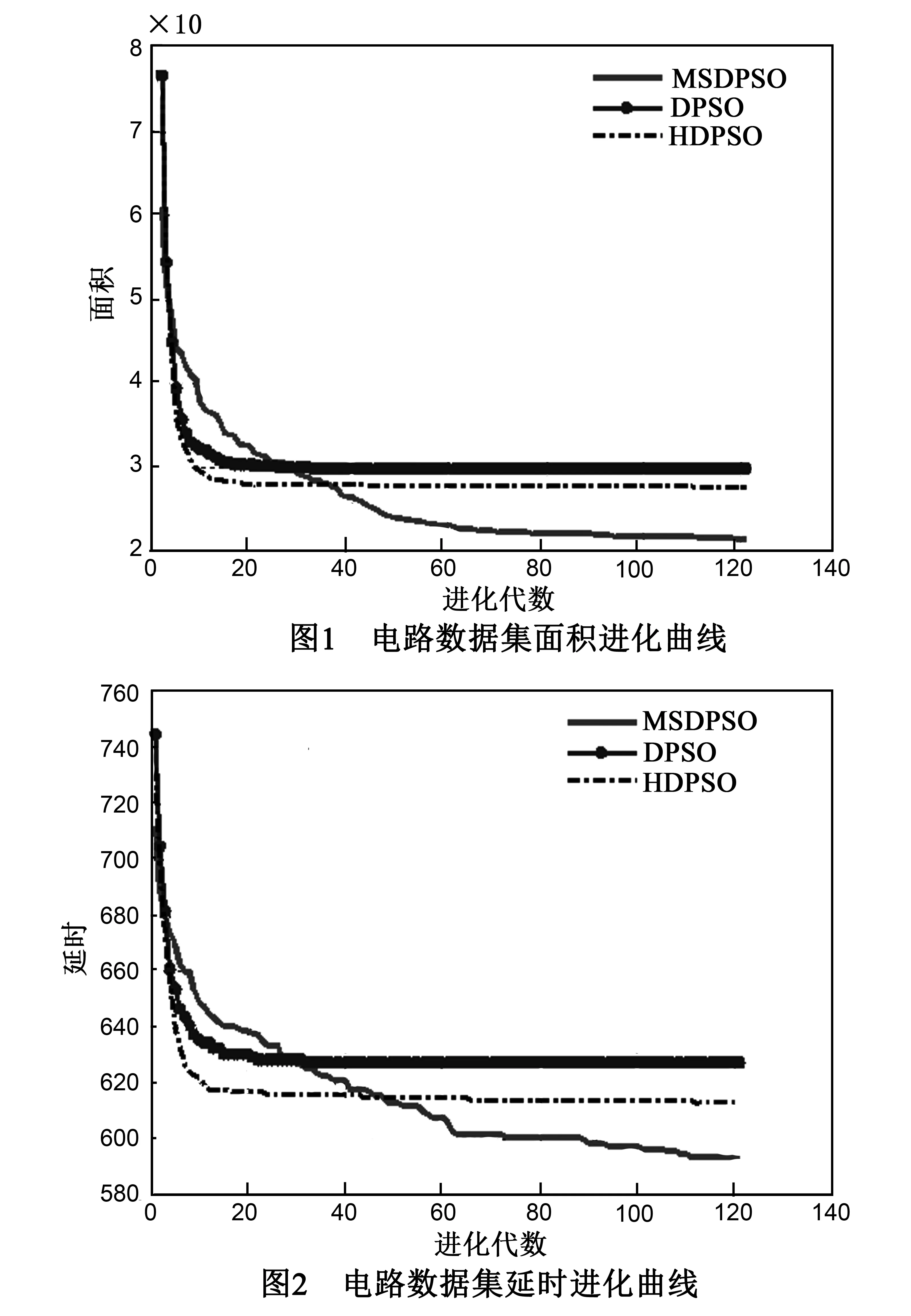
图1、图2显示，DPSO算法和HDPSO算法在20代左右已经陷入局部最优解，出现进化停滞.而MSDPSO算法由于具有探索与开发并行能力，因此能够在整个迭代过程中都保持不断进化的动力，预防粒子种群发生早熟情况，具有更好的优化性能.

6　结束语

MPRM电路具有较大的极性搜索空间，有必要寻找一种搜索性能强的智能优化算法来实现电路延时与面积优化设计.本文通过对MPRM电路和粒子群算法的研究，提出一种基于多策略离散粒子群算法的MPRM电路延时与面积优化方法.在种群内部划分不同策略的团队，并行协作完成全局探索和局部开发任务，提高了算法的优化能力.对15个PLA格式的MCNC Benchmark电路进行了测试，实验结果表明与已有文献相比较，MSDPSO算法具有更好的优化效率.

[1]卜登立,江建慧.基于对偶逻辑的混合极性 RM 电路极性转换和优化方法[J].电子学报,2015,43(1):79-85.

Bu D L,Jiang J H.Dual logic based polarity conversion and optimization of mixed polarity RM circuits[J].Acta Electronica Sinica,2015,43(1):79-85.(in Chinese)

[2]周雅兰,王甲海,黄聪.求解排列问题的分布估计离散粒子群优化算法[J].电子学报,2014,42(3):561-571.

Zhou Y L,Wang J H,Huang C.Estimation of distribution-discrete particle swarm optimization algorithm for permutation-based problems[J].Acta Electronica Sinica,2014,42(3):561-571.(in Chinese)

[3]Yu S W,Wang K,Wei Y M.A hybrid self-adaptive particle swarm optimization-genetic algorithm-radial basis function model for annual electricity demand prediction[J].Energy Conversion and Management,2015,91:176-185.

[4]郑巧仙,李明,李元香,等.求解双边装配线平衡问题的改进蚁群算法[J].电子学报,2014,42(5):841-845.

Zheng Q X,Li M,Li Y X,et al.An improved ant colony optimization for two-sided assembly line balancing problem[J].Acta Electronica Sinica,2014,42(5):841-845.(in Chinese)

[5]俞海珍,蒋志迪,汪鹏君,等.GA-DTPSO算法及其在混合极性XNOR/OR电路面积优化中应用[J].计算机辅助设计与图形学学报,2015,27(5):946-952.Yu H Z,Jiang Z D,Wang P J,et al.GA-DTPSO algorithm and its application in area optimization of mixed polarity XNOR/OR circuits[J].Journal of Computer-Aided Design and Computer Graphics,2015,27(5):946-952.(in Chinese)

[6]卜登立,江建慧.基于混合多值离散粒子群优化的混合极性Reed-Muller最小化算法[J].电子与信息学报,2013,35(2):361-367.

Bu D L,Jiang J H.Hybrid multi-valued discrete particle swarm optimization algorithm for mixed-polarity reed-muller minimization[J].Journal of Electronics and Information Technology,2013,35(2):361-367.(in Chinese)

[7]李辉，汪鹏君，王振海.混合极性列表技术及其在MPRM电路面积优化中的应用[J].计算机辅助设计与图形学学报,2011,32(3):527-533.

Li H,Wang P J,Wang Z H.Tabular techniques for mixed-polarity and its application in area optimization of MPRM circuits[J].Journal of Computer-Aided Design and Computer Graphics,2011,32(3):527-533.(in Chinese)

[8]Hrynkiewicz E,Kotodziński S.An Ashenhurst disjoint and non-disjoint decomposition of logic functions in Reed-Muller spectral domain[A].Proceedings of Mixed Design of Integrated Circuits and System[C].Warsaw:IEEE,2010.200-204.

[9]王振海，汪鹏君，俞海珍,等.基于PSO算法的FPRM电路延时和面积优化[J].电路与系统学报.2012,17(5):75-80.

Wang Z H,Wang P J,Yu H Z,et al.Delay and area optimization for FPRM circuits based on PSO algorithm[J].Journal of Circuits and Systems,2012,17(5):75-80.(in Chinese)

[10]Jiang Z D,Wang Z H,Wang P J.Delay-area trade-off MPRM circuits based on hybrid discrete particle swarm optimization[J].Journal of Semiconuctors,2013,34(6):065007.

[11]Du W,Li B.Multi-strategy ensemble particle swarm optimization for dynamic optimization[J].Information Sciences,2008,178(15):3096-3109.

[12]Wang H,Wu Z,Rahnamayan S,et al.Multi-strategy ensemble artificial bee colony algorithm[J].Information Sciences,2014,279:587-603.

符强男,1975年出生,江西赣州人.博士研究生,讲师,主要研究方向为低功耗集成电路理论及优化设计.

E-mail：fuqiang@nbu.edu.cn

汪鹏君(通信作者)男,1966年出生,浙江奉化人.博士,教授,博士生导师,中国电子学会高级会员,中国计算机学会高级会员,中国电子学会电子线路与系统专业委员会委员,中国计算机学会多值逻辑与模糊逻辑专业委员会委员.主要研究方向为多值逻辑和低功耗集成电路理论及优化设计.

E-mail：wangpengjun@nbu.edu.cn

Delay and Area Optimization for MPRM Circuits Based on Multi-strategy Discrete Particle Swarm Optimization

FU Qiang1,2,WANG Peng-jun1,TONG Nan2,WANG Ming-bo2,ZHANG Hui-hong1

(1.InstituteofCircuitsandSystems,NingboUniversity,Ningbo，Zhejiang315211，China;2.CollegeofScienceandTechnology,NingboUniversity,Ningbo,Zhejiang315212,China)

In order to improve the delay and area design of large-scale MPRM circuits,the multi-strategy discrete particle swarm optimization(MSDPSO)is proposed.In MSDPSO,the particles were divided into several teams with different strategy,and each team cooperated with others to promote the exploration and exploitation of the particle population.Meanwhile,the Gaussian adjustment was adopted to activate the worse individuals.Combined with MSDPSO and tabular technique,the best polarity of delay and area was searched for large-scale MPRM circuits.MCNC Benchmarks with PLA format are tested to verify the effectiveness of the MSDPSO,and the results show that MSDPSO has achieved an average saving of 8.46% and 38.73% on delay and area respectively in comparison with the DPSO.

multi-strategy discrete particle swarm optimization(MSDPSO)；MPRM circuits；delay and area optimization；polarity search

2015-12-09；

2016-02-04；责任编辑：马兰英

国家自然科学基金(No.61306041，No.61234002)；宁波市自然科学基金(No.2014A610069);浙江省教育厅科研项目(No.Y201326770)

TP391.72

A

0372-2112 (2016)05-1202-06

电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.027