基于向量投影TOPSIS法的资源均衡优化

王栎绮,何立华(中国石油大学(华东)经济管理学院,山东青岛　266580)

基于向量投影TOPSIS法的资源均衡优化

王栎绮,何立华
(中国石油大学(华东)经济管理学院,山东青岛266580)

针对资源均衡优化问题,定义了一种基于向量投影的TOPSIS指标为资源均衡性度量的新指标.对于多个资源均衡优化方案,首先确定正、负理想优化方案,计算各方案在正、负理想方案上的向量投影,然后计算各个方案的相对贴近度,再根据相对贴近度的大小衡量各个优化方案的优劣.该指标可以有效避免当采用传统的均值、方差或熵等度量指标评价某几个优化方案时,同一度量指标下这几个优化方案的目标函数值都相等而无法对这几个优化方案进行区别的不足.其次,构建了基于向量投影的TOPSIS为度量指标的资源均衡优化模型,并针对该模型设计了相应的粒子群算法.最后,运用一个算例验证分析了所提指标和算法的可行性和有效性.

资源均衡;TOPSIS;向量投影;粒子群算法

引用格式:Wang Liqi,He Lihua．Resources Equilibrium Optimization Based on by TOPSIS of Vector Projection [J]．Journal of Gansu Sciences,2016,28(2):113G118．[王栎绮,何立华．基于向量投影TOPSIS法的资源均衡优化[J]．甘肃科学学报,2016,28(2):113G118．]

资源均衡问题是指在项目工期保持不变的情况下,通过合理调整网络计划中非关键路径上的工序,尽量避免出现资源的高峰和低谷现象,使每天资源需求量趋于均衡的过程[1].资源均衡问题在理论上已被证明是NPGhard组合优化问题[2],在实践中有着广泛的应用价值.关于资源均衡问题的研究,一直吸引着国内外众多学者和实际工作者的关注,并从不同角度提出了各种资源均衡优化的模型和算法[3G5].在资源均衡优化模型中,学者们提出了多种衡量资源均衡性的度量指标,以绝对偏差最小作为度量资源均衡性的指标[6,7],以每天资源需求量的平方和作为目标函数[8,9],以矩最小来评价项目的资源均衡性[10G12],这些指标虽易操作、简单明了,但其误差较大.为了更好地反映优化方案的资源均衡性,有学者提出了以方差作为资源均衡性的度量指标[13,14].此外,何大义等[15]提出的极大熵准则可知,熵本身是一个连续的函数,熵越大该分布就越接近于均匀分布.对此,文献[16G18]中提出以资源熵作为目标函数,来度量各个优化方案的资源均衡性.研究基于逼近理想解排序法(TOPSIS,technique for order perference by similarity to ideal solution)指标为资源均衡性度量标准的新指标,来评价多个资源均衡优化方案的优劣.

1　基于向量投影TOPSIS法的指标

1．1相关概念

首先,给出向量投影和相对贴近度等概念.

由于不同的评价属性具有不同的量纲,因此在决策之前需要对属性进行无量纲和同趋化处理.对于具有多个属性的方案X＝(xij)m×n,可以进行规范化处理: j＝1

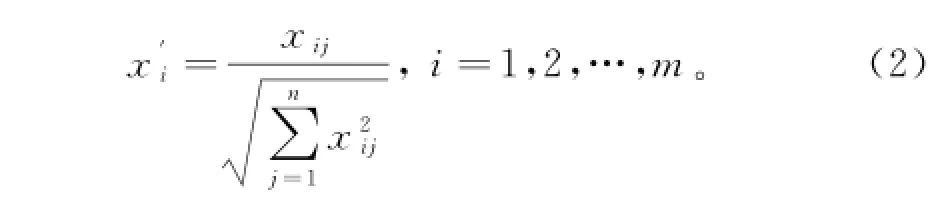
对于资源均衡优化方案来说,要求每天资源需求量越趋于均衡越好.对此,可以将每个均衡优化方案Xi中的资源需求量看作一个向量,先将向量的每一维作简化处理,该指标越小越好.如果有多种资源,在简化处理后,再对每一种资源作规范化处理.方案Xi同趋化处理后记作Pi＝

定义2称为决策方案的正理想方案,其中:

定义3称为决策方案的负理想方案,其中:

定义4TOPSIS是一种逼近于理想解的排序法,可以采用相对贴近度的大小表示方案Xi与其他方案的接近程度[20],记作其中:PrXi＋表示方案Xi在正理想方案上的向量投影;PrXi－表示方案Xi在负理想方案上的向量投影. Ci(Ci∈0,1[])越大,表示该方案越接近正理想方案,说明方案Xi越优[21].

1．2传统度量指标计算现假设有A、B、C三个方案,分别以均值、方差、熵值及基于向量投影的TOPSIS作为度量指标对这三个方案进行评价.A、B、C三个方案数据值如表1所列.表1中数字代表每天该方案的波动性,方案要求越趋于均衡越好.

(1)以均值为度量指标,有

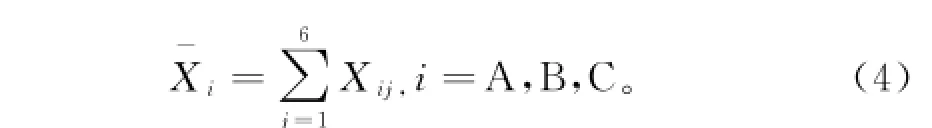
(2)以方差为度量指标,有

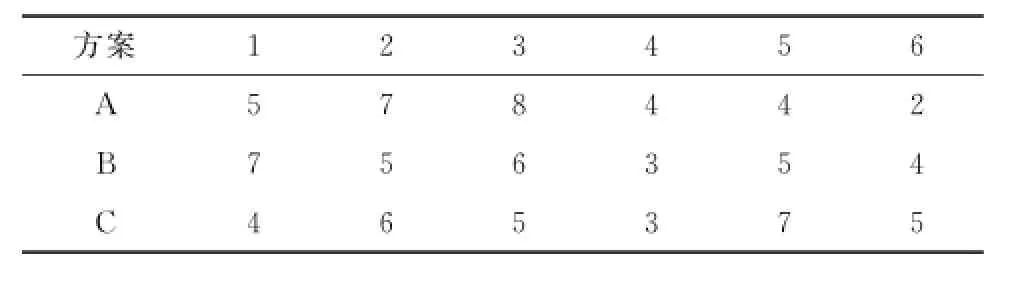
表1　A、B、C三个方案数据值Table 1　Data value of A,B and C scheme

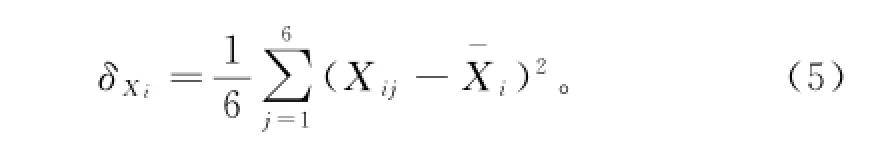
(3)以熵值为度量指标[16],有

根据式(4)~式(6),分别以均值、方差、熵值衡量三个方案的均衡性,计算结果如表2所列.

表2　计算结果Table 2　Calculation results table

1．3基于向量投影TOPSIS的新指标

表3　处理后的A、B、C三个方案Table 3　A,B and C scheme after treating

(2)确定正、负理想方案根据定义2和定义3,分别确定正理想方案和负理想方案,如表4所列.

表4　正、负理想方案Table 4　Positive and negative ideal optimization schemes

(3)计算三个方案在正、负理想方案上的向量投影根据式(1),A、B、C三个方案在正、负理想方案上的向量投影分别为

(4)计算各个方案的相对贴近度根据公式(3),A、B、C三个方案的相对贴近度分别为

由于CA＜CB＜Cc,因此C方案优于B方案优于A方案.从上述计算分析可以看出,以基于向量投影的TOPSIS作为均衡性度量指标,可以对采用传统度量指标不能区分的方案进行区别.

2　问题描述与模型构建

资源均衡优化是指在项目工期固定的情况下,通过合理调整网络计划中非关键路径上的工序,使资源需求量趋于均衡的过程.在均衡优化中,假设满足以下条件[12,22]:项目总工期一定;各个活动的持续时间不变,且在活动的持续时间内所需要的资源量不变,对项目的重要程度都一样;活动间的逻辑关系不变;活动是连续的;资源供应在各个时期是充足的,即不考虑资源供给的限制;活动为单模式.在此,以基于向量投影的TOPSIS为指标构建资源均衡优化模型,有

式(7)表示各优化方案的相对贴近度,要求越大越好; PrXj＋表示优化方案Xj在正理想优化方案Pr＋上的投影,PrXj－表示优化方案Xj在负理想优化方案Pr－上的投影.式(8)表示优化方案Xj在正、负理想方案上的投影.为了书写方便,用b表示正负理想方案,j表示优化方案个数,bn表示正、负理想优化方案中第n天的资源消耗量.式(9)表示活动i的实际开始时间与其最早开始时间之差不超过其总时差,ti表示活动i的实际开始时间,ESi表示活动i的最早开始时间, TFi表示活动i的总时差.式(10)表示各个活动的持续时间非负,I表示活动数.

3　算法

粒子群算法(PSO,particle swarm optimizaG tion)是模拟生物群体行为而构造的一种随机搜索算法[23].粒子在飞行的过程中,用一个速度决定它们飞行的方向和距离,所有粒子通过追随当前最优粒子在解的空间中进行搜索[24].粒子群中粒子在寻优的过程中,根据式(11)~式(12)来更新自己的速度和位置[25]:

式(11)表示粒子速度的更新,其中:非负常数w为惯性因子,通常情况下w在[0．4,0．9]范围内取值;非负常数c1和c2为学习因子,一般取c1＝c2＝2; r1、r2为[0,1]范围内的随机数[16].式(12)表示粒子位置的更新.

用粒子群算法求解资源均衡优化问题,以活动数N表示粒子空间探索维数[16],在此,粒子规模取30个.满足约束条件式(9)和式(10)的一组活动的开始时间为Sj＝(sj1,sj2,ƻ,sjn)(j＝1,2,ƻ,M).为了保证生成的优化方案可行,粒子飞行的位置需要限制在一定范围内.由于每个活动的实际开始时间在其最早开始时间ESj和最晚开始时间LSj内变化,因此设定粒子位置xj的变化范围为xj∈[ESj,LEj].粒子通过不断地迭代更新,达到最佳适应度值,即此时所对应的粒子的位置即为问题的一个可行解.

4　算例分析

采用文献[17]中的算例,该项目中每个活动对项目的重要程度相同且均需要消耗一种资源.为了更加符合实际,将活动H的资源需求量由原文中的0改为3,各个活动的持续时间和资源需求量如图1所示.

4．1不同优化方案比较

根据单代号网络图,用粒子群算法通过MATG LAB编程计算,项目工期T＝16天.选择不同相对贴近度下的8种资源均衡优化方案,这8种方案每天的资源需求量如表5所列.

(1)计算每天资源需求量平均值.通过计算,8个方案中每天资源需求量平均值相等,即＝7.

图1　项目单代号网路Fig．1　Program list code network

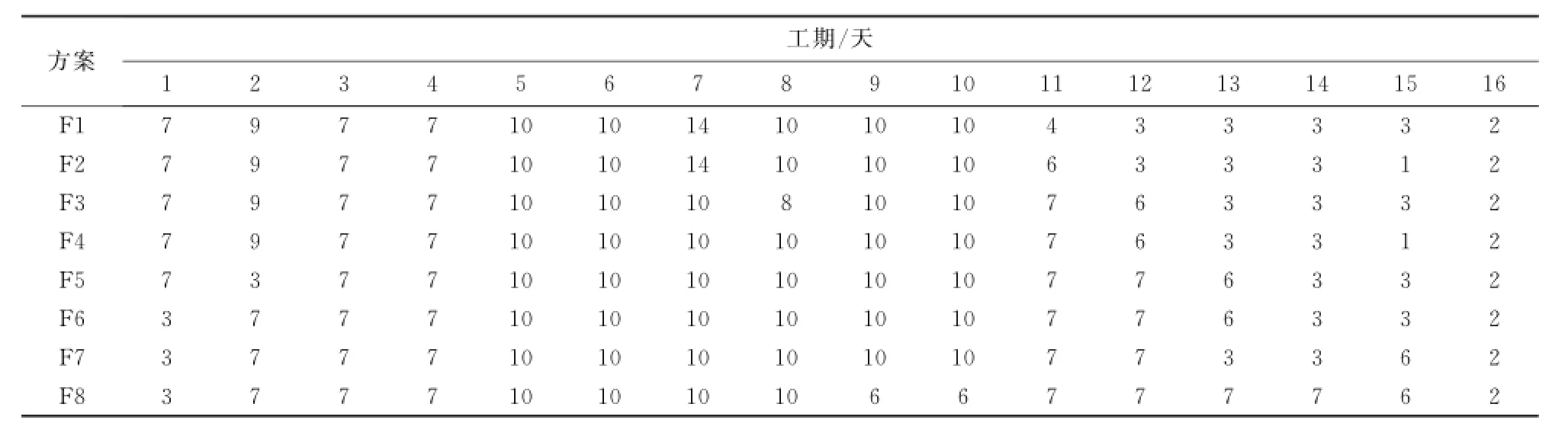
表5　每天资源需求量Table 5　Daily resources demand table

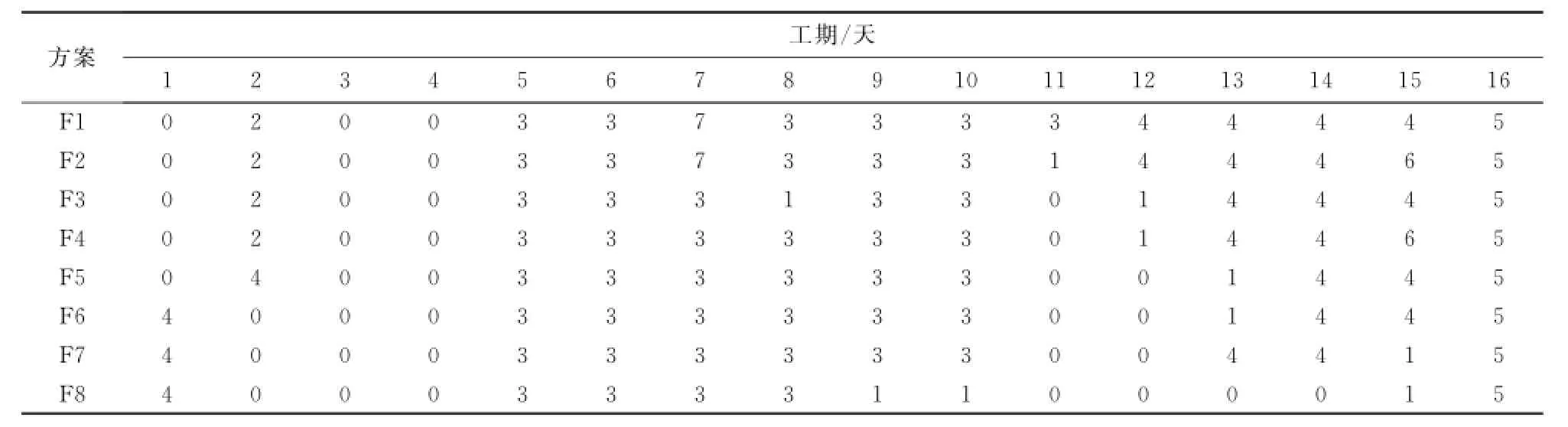
表6　每天资源需求量偏差Table 6　Deviation of daily resource requirements

(3)确定正、负理想优化方案.按照定义2和定义3确定正、负理想优化方案,每天资源需求量如表7所列.

(4)计算各方案在正负理想方案上的向量投影.根据向量投影概念及式(1)计算,得

表7　正、负理想方案每天资源需求量Table 7　Daily resource requirements of positive and negative ideal scheme

(5)计算各优化方案的相对贴近度.根据相对贴近度的概念和公式(3)计算,得

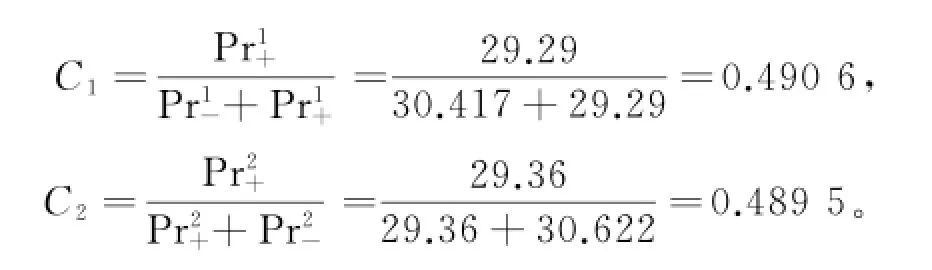
同理有

4．2三种指标计算结果对比

通过以上计算可以看出,方案8优于其余各个方案.现分别以方差、资源熵、相对贴近度三个指标作为资源均衡优化度量指标,对各个方案的优化结果进行对比分析,三种均衡性度量指标计算结果如表8所列.

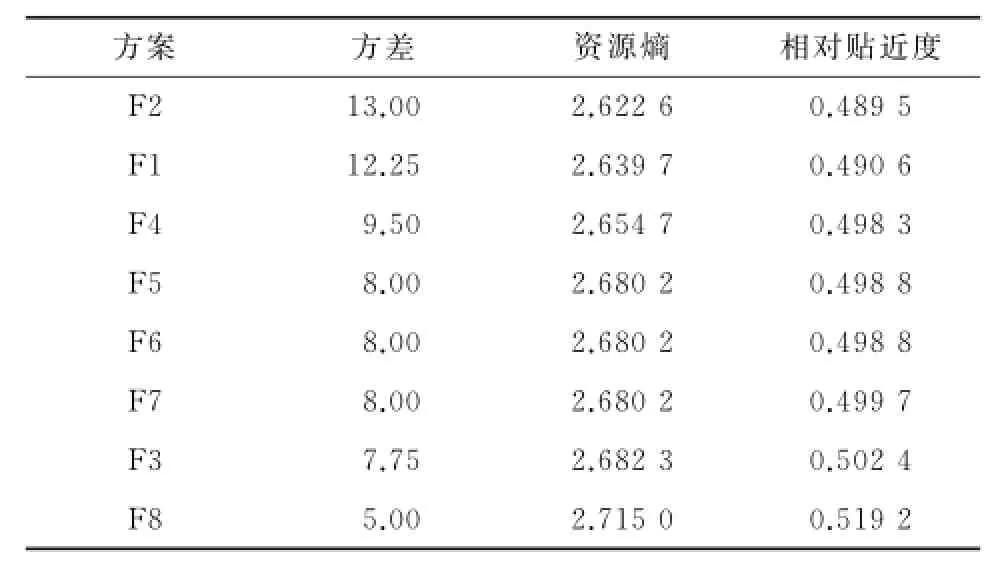
表8　三种指标计算结果Table 8　Calculation results of three indexes

将8种优化方案的计算结果按照相对贴近度的大小从小到大排序,见表8.从表8可以看出,以方差或熵作为资源均衡性度量指标,方案5、方案6和方案7的目标函数值都相等,即难以对这三个方案进行区别.而当以基于向量投影的TOPSIS作为资源均衡性度量指标,可以看出方案7优于方案5和方案6.对于方案5和方案6,方案5在第一天和第二天所需资源量分别是7和3,方案6在第一天和第二天所需资源量分别是3和7.相应的,正理想优化方案中第一天和第二天所需资源量分别是7和7,负理想优化方案中第一天和第二天的资源量分别是3和3,因此方案5和方案6的相对贴近度相等.

此外,比较表8中三种度量指标下各个方案均衡性计算结果,不仅可以看出,以基于向量投影的TOPSIS作为资源均衡性度量指标,各个优化方案的优劣排序与以方差或熵为度量指标的排序一致,而且对采用传统度量指标如方差、熵等难以区别的方案5、方案6及方案7可以进行甄别,并能找到最优方案(方案8最优).因此,以研究所提的基于向量投影的TOPSIS作为资源均衡性度量指标,具有可行性和有效性.

5　结语

定义了一种基于向量投影的TOPSIS指标作为资源均衡性度量新指标.对于工程项目的某几种资源均衡优化方案,这一指标不仅避免了当采用传统的均值、方差或熵等指标来衡量其均衡性时,同一度量指标下这几个优化方案的目标函数值都相等而无法对这几个方案进行甄别的不足,还可以在多个优化方案中找到最优方案.以基于向量投影的TOPSIS作为均衡性度量指标,不仅能够解决各种拓展的资源均衡优化问题,而且可以用于各种项目调度问题、方案评选以及群决策等问题中.

[1]Koulinas G K,Anagnostopoulos K P．A New Tabu SearchG based HyperGheuristic Algorithm for Solving Construction Leveling Problems with Limited Resource Availabilities[J]．Automation in Construction,2013,31:169G175．

[2]Blazewicz J,Lenstra J K．Scheduling Subject to Resource ConG straints Classification and Complexity[J]．Discrete Applied Mathematics,1983,5(1):11G24．

[3]Drótos M,Kis T．Resource Leveling in a Machine Environment [J]．European Journal of Operational Research,2011,212(1): 12G21．

[4]庞南生,纪昌明．广义时序下活动多模式与离散型资源均衡优化[J]．系统工程学报,2011,26(4):538G545．

[5]Hariga M A,EIGSayegh S M．Cost Optimization Model for the MultiGresource Leveling Problem with Allowed Activity SplitG ting[J]．Journal of Construction Engineering and ManageG ment,2011,137(1):56G64．

[6]Said M E．Resource Leveling in Construction by Optimization [J]．Journal of Construction Engineering and Management, 1989,115(2):302G316．

[7]Senouci A B,Eklin N N．Use of Genetic Algorithms in ReG source Scheduling of Construction Projects[J]．Journal of Construction Engineering and Management,2004,130(6):869G877．

[8]Tarek H．Optimization of Resource Allocation and Leveling UG sing Genetic Algorithms[J]．Journal of Construction EngiG neering and Management,1999,125(3):167G175．

[9]Son J,Skibniewski M J．MultiGheuristic Approach for Resource Leveling Problem in Construction Engineering:Hybrid ApG proach[J]．Journal of Construction Engineering and ManageG ment,1999,125(1):23G31．

[10]徐哲,贾子君,李科．工程项目资源均衡优化的混合遗传算法研究[J]．数学的实践与认识,2011,41(6):24G29．

[11]Hiyassat M．Applying Modified Minimum Moment Method to Multiple Resource Leveling[J]．Journal of Construction EngiG neering and Management,2001,127(3):192G198．

[12]Christodoulou SE,Ellinas G,Michaelidou K A．Minimum MoG ment Method for Resource Leveling Using Entropy MaximiG zation[J]．Journal of Construction Engineering and ManageG ment,2010,136(5):518G527．

[13]王祖和,亓霞．多资源均衡的权重优选法[J]．管理工程学报, 2002,16(3):91G93．

[14]田丰春,杨种学,杨宁．虚拟样机工程中的项目资源均衡优化研究[J]．计算机工程与科学,2011,33(12):184G188．

[15]何大义,邱菀华．运用熵极大化准则求解连续型不确定性决策问题[J]．系统工程理论与实践,2002,22(9):97G100．

[16]乞建勋,王强,贾海红．基于熵权和粒子群的资源均衡新方法研究[J]．中国管理科学,2008,16(1):90G95．

[17]Symeon Christodoulou,Georgios Ellinas,Pooyan Aslani．EntropyG based Scheduling of ResourceGconstrained Construction Projects [J]．Automation in Construction,2009,18(7):918G928．

[18]丁继勇,王卓甫,李慧敏．配套施工条件下水电工程多资源均衡优化[J]．水力发电学报,2013,32(5):299G305．

[19]杨静,邱菀华．基于离差的模糊多属性决策法及其应用[J]．系统工程,2008,26(6):107G110．

[20]屈文阁．一种区间数多属性决策方法在经济评价中的应用[J]．甘肃科学学报,2013,25(4):152G155．

[21]周宏安,刘三阳．基于离差最大化模型的模糊多属性决策投影法[J]．系统工程与电子技术,2007,29(5):741G744．

[22]陆惠民,杜训．工程项目资源优化的混合整数规划算法[J]．东南大学学报:自然科学版,1991,21(4):123G129．

[23]刘琦铀,施灿涛,李铁克．基于混合粒子群算法的工艺规划与调度集成问题研究[J]．工业工程与管理,2013,18(6):20G26．

[24]陈志勇,杜志达,周华．基于微粒群算法的工程项目资源均衡优化[J]．土木工程学报,2007,40(2):93G96．

[25]彭武良,郝永平．求解资源受限项目调度问题的改进粒子群算法[J]．系统工程,2010,28(4):84G88．

Resources Equilibrium Optimization Based on by TOPSIS of Vector Projection

Wang Liqi,He Lihua
(School of Economics and Management,China University of Petroleum,Qingdao 266580,China)

A new index for measuring resource equilibrium is defined on the basis of TOPSISindex of vecG tor projection for the problems of resources equilibrium optimization．For multiGresources equilibrium optiG mization schemes,first,positive and negative ideal optimization schemes shall be determined to calculate its vector projection and then its relative closeness which is used to measure its advantages and disadvantages in reverse．This index can effectively avoid the disadvantages of being unable to distinguish several optimiG zation schemes when they are evaluated by traditional measurement indexes like mean,variance,entropy and so on,which has same objective function valve under the same measurement index．Second,the relevant particle swarm optimization is designed based on resources equilibrium optimization model which is build on the basis of the measurement index TOPSIS of vector projection．Third,the feasibility and effectiveness of the indexes and algorithms mentioned are analyzed through applying example verification．

Resource equilibrium;TOPSIS;Vector projection;Particle swarm optimization

F062．1

A

1004G0366(2016)02G0113G06

10．16468/j．cnkii．ssn1004G0366．2016．02．024．

2015G06G13;

2015G09G14．

山东省自然科学基金项目(ZR2015GM009);中央高校基本科研业务费专项基金(15CX05007B)．

王栎绮(1989G),女,硕士研究生,研究方向为工程项目管理．EGmail:wangliqi369369＠163．com．