GM(1,1)模型的改进及其在西安市人口预测中的应用

王建芳(西安铁路职业技术学院,陕西西安　710016)

GM(1,1)模型的改进及其在西安市人口预测中的应用

王建芳
(西安铁路职业技术学院,陕西西安710016)

人口规模对大中型城市的发展非常重要,为提高人口预测模型的预测精度,分析了GM(1,1)和等维递补动态预测模型的特点,并以2007—2012年西安市人口数据资料为依据,应用灰色系统理论构建等维递补GM(1,1)动态预测模型,预测了西安市2013—2016年城市人口规模,结果分别为859．757 3万人(2013年),864．010 6万人(2014年),868．285 0万人(2015年),872．580 5万人(2016年).统计检验和误差分析结果表明,该模型方法简便可行,预测精度高,结果符合实际,可靠性强,为市域经济发展的研究和决策提供了科学依据.

GM(1,1)模型;等维递补模型;人口预测

引用格式:Wang Jianfang．Improvement of GM(1,1)Model and Its Application of Population Prediction of Xi’an City[J]．Journal of Gansu Sciences,2016,28(2):10G13．[王建芳．GM(1,1)模型的改进及其在西安市人口预测中的应用[J]．甘肃科学学报,2016,28(2):10G13．]

人口问题一直是制约社会发展的第一因素,直接影响经济的发展和资源的利用.因此,预测未来人口规模有着重要的现实意义,对大中型城市显得尤为重要.但是,由于影响城市人口规模变化的因素众多,且有些因素是不确定的,从而增加了资料获取的难度,影响预测结果的精度.1982年邓聚龙[1]提出灰色系统理论,作为其重要内容之一的GM(1, 1)模型,它的特点是所需信息量少,建模过程简单,易于求解,在管理、经济和工程方面得到了广泛应用[2].但它也存在着很多缺陷,如当发展系数的绝对值较大时,模型偏差较大,无法用于中长期预测.因此,近年来不少学者提出了对GM(1,1)模型的改进[3G6],研究用等维递补GM(1,1)动态预测模型对西安市人口规模进行了预测,预测结果明显优于一般的GM(1,1)模型.

1　模型原理及计算方法

1．1GM(1,1)模型

其基本思想是把一组离散的、随机的原始数据序列经r次累加生成规律性强的累加生成序列,从而达到使原始序列随机性和波动性弱化的目的,然后对累加生成序列建模,最后进行r次累减还原成预测值.累加生成次数愈多,随机性被弱化得愈显著,序列所形成的曲线其规律性将更加明显.研究以1GAGO为例,具体步骤如下:

(1)累加(1GAGO)序列x(1)的生成

设原始序列为x(0)＝(x(0)(1),x(0)(2),ƻ, x(0)(n)),则有

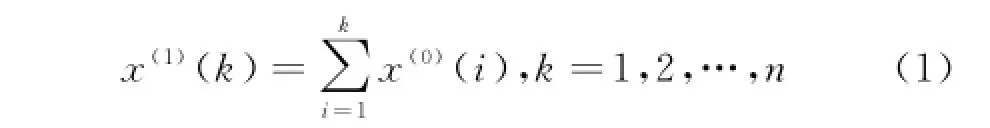
(2)加权邻值序列z(1)的生成

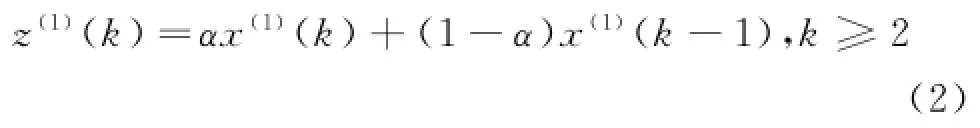
其中:x(1)(k－1),x(1)(k)为序列的前后邻值,常数α为生成系数,α∈[0,1].当α＝0．5时,生成均值序列

(3)建立GM(1,1)模型

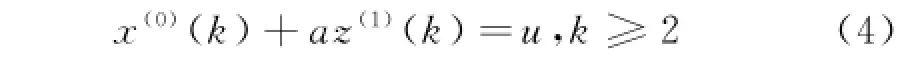
其中:a,u是参数;a为发展灰数;u为内生控制灰数.

(4)用最小二乘法求参数

其中:

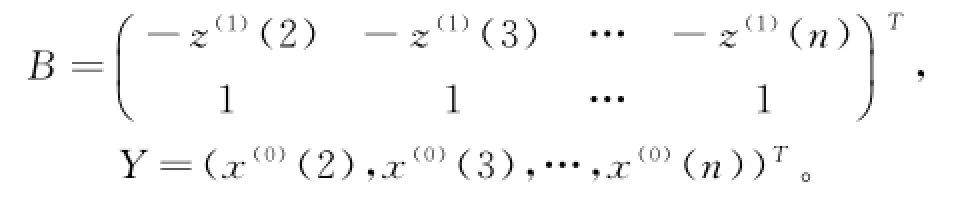
(5)计算拟合值,并累减(IGAGO)还原,对应的白化方程为

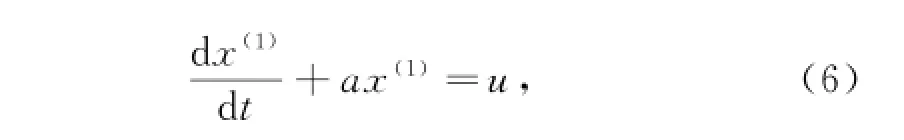
方程解为

于是预测值为

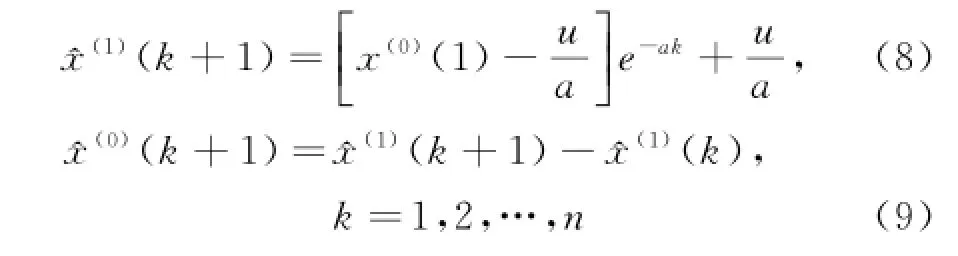
(6)模型精度检验

一个模型必须通过精度检验合格后才能应用于实际问题.GM(1,1)模型的检验包括残差检验,后验差检验和小误差概率检验[7,8].检验等级见表1.

表1　精度检验等级分类Table 1　Grade classification of accuracy test

残差检验公式为

其中相对误差为

后验差比值C为

其中:S1,S2分别为原始数据和残差的均方差,＝

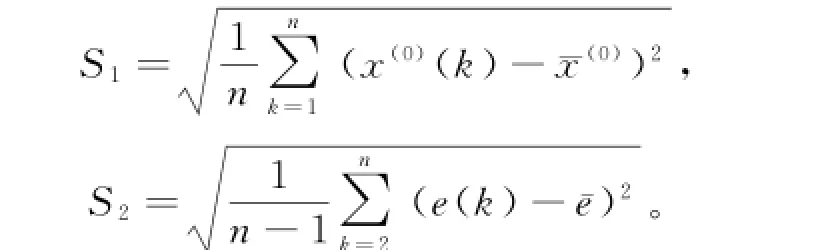
小误差概率P为

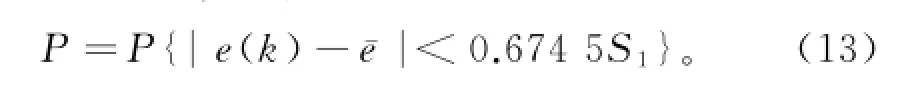
检验时相对误差和比值C越小,小误差概率P则越大,说明模型精度越好.其中C和P中只要一个符合标准,就认为满足相应的精度要求.如果不满足精度要求,可根据残差序列建立带有残差的GM(1,1)或Verhulst模型进一步修正,直至满足精度要求.

1．2等维递补GM(1,1)模型

等维递补GM(1,1)模型是对传统静态GM(1,1)模型的动态使用,通过不断补充新信息使灰度逐步降低.其基本原理是将GM(1,1)模型预测的第一个值补充在已知序列后,为保持数据序列的等维,同时去掉原序列的第一个已知数据,然后再建立GM(1,1)模型,预测下一个值,如此新陈代谢,逐个预测,依次递补,直至完成预测目的或达到一定的精度要求.该模型相对GM(1,1)模型的优点:①及时补充和利用新信息,提高了灰区间的白化度,比GM(1,1)模型预测更合理,更接近实际.②每预测一步模型灰参数做一次修正,如此以来,在灰参数不断修正的同时,模型会逐步得到改进,预测精度也会提高.当然随着递补次数的增加灰度也在增大,有用信息量反而会减少.因此,递补预测也不是无止境的.

2　实证分析——以西安市为例

根据«西安统计年鉴»[9]人口统计数据资料,预测2013—2016年西安市人口规模.由于样本数量少,信息量少,普通的时间序列建模和预测方法无法使用.但是依据灰色预测的短序列、现时性和贫信息等特点,易知灰色数列预测法较为合适.为此,首先对现有数据进行选择与处理,然后采用灰色GM(1,1)法和等维递补法建模并预测,确定出人口规模(见表2),并对结果进行精度检验(见表3).

表2　拟合及预测人口数Table 2　Fitting and predicted population number万人

表3　拟合精度检验结果Table 3　Fitting precision test results

2．1数据资料收集

用“小样本”数据作预测是灰色预测法的特长,即建模维数不宜太大,一般5~8个数据较为适宜.遵循“现实信息优先原则”,选取2007—2012年西安市人口数据资料为预测样本(见表4),即

表4　2007—2012年西安市实际人口数Table 4　Actual population number of Xiƴan City from 2007 to 2012万人

2．2数据处理

为弱化原始数据序列的随机性和波动性,由式(1)对x(0)进行一次累加生成,得到新序列x(1),即

2．3GM(1,1)预测模型建立采用最小二乘法求解参数a,u

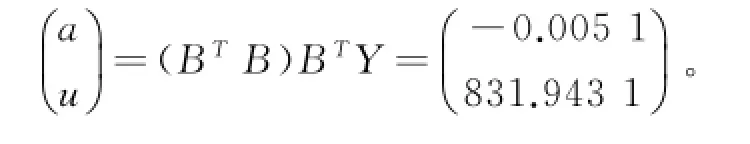
将a,u代入式(8),得到预测模型为

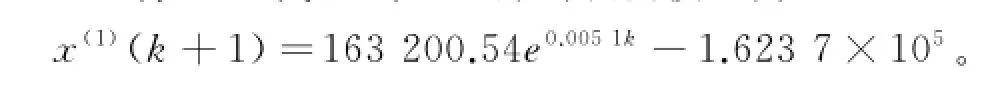
运用后减运算还原得到2013—2016年人口规模为

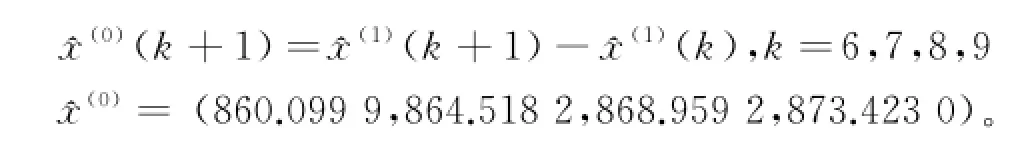
2．4等维递补GM(1,1)预测模型建立

为了降低灰度,对预测样本采用逐年递补,通过不断补充新信息,对模型灰参数做修正,如此在灰参数不断修正的同时,模型会逐步得到改进,预测精度也会提高.通过三次递补预测了2013—2016年人口规模,预测模型分别为

2．5精度检验

对以上两种模型的预测结果,分别利用式(10)~(13)进行残差检验、后验差检验和小误差概率检验.检验等级见表1,结果见表3.

计算2012年和2013年实际值和4次预测值的相对误差,结果为

可见,等维递补模型拟合精度高于一般的GM(1,1)模型.

3　结论

由精度检验等级可知,GM(1,1)模型和等维递补模型拟合精度均符合要求,模型可用于外推预测,但通过比较检验结果,等维递补模型拟合精度高于一般的GM(1,1)模型.分析表明,西安市2013—2016年城市人口数量呈持续上升状态,预测结果符合实际,为市域经济发展的研究和决策提供了科学依据.由此可见,对于短序列、贫信息的人口预测,等维递补动态预测不失为一种有价值的方法,具有较高的预测精度,有很好的通用性和推广性,可推广应用于其他城市人口数据预测中.

[1]邓聚龙．灰色预报与决策[M]．武汉:华中理工大学出版社, 1988．

[2]焦宝聪,陈兰平．运筹学的思想方法及应用[M]．北京:北京大学出版社,2008．

[3]魏玉明,党星海,赵建赟,等．不等间距GM(1,1)模型在滑坡监测分析中的应用[J]．甘肃科学学报,2010,22(2):38G40．

[4]叶谦．GM(1,1)模型的改进及其在银行贷款中的应用[J]．数学的实践与认识,2008,38(18):20G27．

[5]尚军亮,方敏．一种优化的高精度灰色GM(1,1)预测模型[J]．电子与信息学报,2010,32(6):1 301G1 305．

[6]侯运炳,汪健民,张晓,等．改进的灰色预测模型在煤矿成本预测中的应用[J]．中国矿业,2013,22(5):49G52．

[7]张立宁,安晶,张奇,等．基于灰色GM(1,1)模型的桩基沉降预测研究[J]．华北科技学院学报,2012,9(4):45G47．

[8]杨存典,张雁．G(1,1)灰色模型与灰色线性模型预测法比较及应用——以商洛市房地产发展现状为例[J]．甘肃科学学报, 2014,26(6):26G28．

[9]张民伟．西安市统计年鉴[M]．北京:中国统计出版社,2014．

Improvement of GM(1,1)Model and Its Application of Population Prediction of Xi’an City

Wang Jianfang
(Xi’an Railway Vocational&Technical Institute,Xi’an 710016,China)

Population size plays a very important role in the development of large and medium size cities．In order to promote the precision of prediction of population prediction model,the characteristics of GM(1,1) and equalGdimension filling dynamic prediction model is analyzed based on the demographic data informaG tion of Xiƴan City from 2007 to 2012．The urban population size of Xi’an City from 2013 to 2016 predicts 85 975．73 million(in the year of 2013),86 401．06 million(in the year of 2014),86 828．50 million(in the year of 2015),87 258．05 million(in the year of 2016)by using grey system theory to build GM(1,1) equalGdimension filling dynamic prediction model．The results of statistical test and error analysis indicate that this model method is simple and convenient with high prediction accuracy,practical results and strong reliability to provide scientific basis on the study and decisionGmaking of municipal economic development．

GM(1,1)model;EqualGdimension filling model;Population prediction

F224．9

A

1004G0366(2016)02G0010G04

10．16468/j．cnkii．ssn1004G0366．2016．02．003．

2015G08G10;

2015G09G14．

王建芳(1972G),女,陕西西安人,硕士,副教授,研究方向为数学建模及教学改革．EGmail:wjfzxz＠163．com．