高阶Bernoulli多项式和高阶Euler多项式的组合恒等式

杨存典,刘端森(商洛学院数学与计算机科学学院,陕西商洛　726000)

高阶Bernoulli多项式和高阶Euler多项式的组合恒等式

杨存典,刘端森
(商洛学院数学与计算机科学学院,陕西商洛726000)

研究了高阶Bernoulli多项式和高阶Euler多项式的关系,并得到了高阶Bernoulli多项式和高阶Euler多项式的表达式及关系式.运用Bernoulli多项式和Euler多项式的基本性质以及初等方法,对经典Bernoulli多项式和Euler多项式的恒等式进行了推广.

高阶Bernoulli多项式;高阶Euler多项式;恒等式

引用格式:Yang Cundian,Liu Duansen．Combinatorial Identity of HighGorder Bernoulli Polynomial and HighGorG der Euler Polynomial[J]．Journal of Gansu Sciences,2016,28(2):7G9．[杨存典,刘端森．高阶Bernoulli多项式和高阶Euler多项式的组合恒等式[J]．甘肃科学学报,2016,28(2):7G9．]

众所周知,多项式和特殊函数的研究在数论、组合数学、特殊函数中的应用非常广泛[1],引起了许多专家和学者的兴趣.特别是经典Bernoulli多项式、Euler多项式、Bernoulli数和Euler数的研究更是成果斐然. Apostol在文献[2]中研究LipschitzGLerch Zeta函数时将Bernoulli多项式做了有益的推广.雒秋明等在文献[3]中将Euler多项式也做了类似的定义.文献[4G8]中作者给出了Bernoulli多项式和Euler多项式的一些恒等式.研究将在高阶Bernoulli多项式和高阶Euler多项式定义的基础上,得出一些有趣的组合恒等式.

1　定义及引理

定义3第二类Stirling数S( n,k)由下列生成函数定义:

引理1若n是非负整数,λ是复数且R(λ)＞0,则[4]

引理2若n是非负整数,α,λ是实数或复数,R(λ)＞0,则[4]

这里F[ a,b;c;t]表示Gauss超几何函数[1].

2　主要结论

定理1若n是非负整数,α,λ是实数或复数,R(λ)＞0,则有

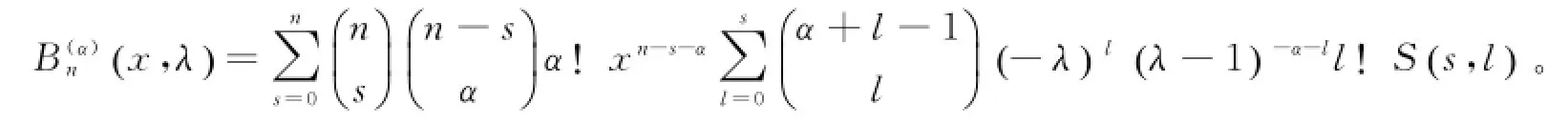
定理2若n是非负整数,α,λ是实数或复数,R(λ)＞0,有加法公式

在式(4)和式(5)中,取λ＝1,α＝1,即得经典加法公式.

定理3若n是非负整数,α,λ是实数或复数,R(λ)＞0,有差分公式

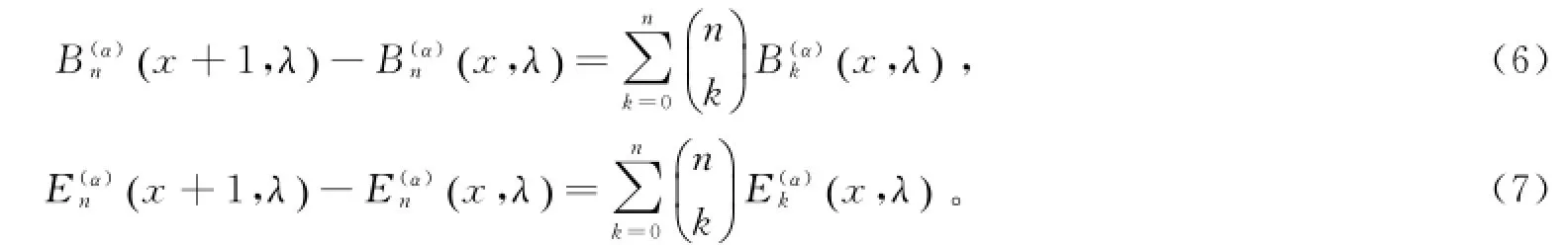
定理4若n是非负整数,α,λ是实数或复数,R(λ)＞0,有组合式

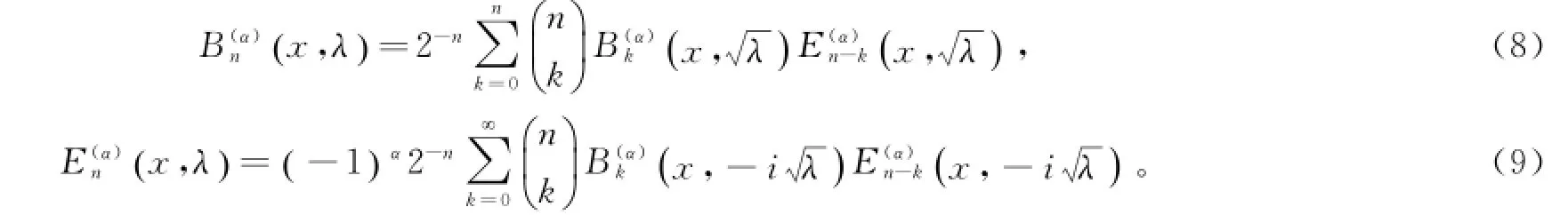
3　定理的证明

对式(1)两边关于t求n阶导数并使用Leibniz法则,得

定理1

由式(1)可得Bn(α)( x＋y,λ)的生成函数是

比较两边系数即得定理2的式(4).同理可得定理2的式(5).

由定义可得

由定义1得

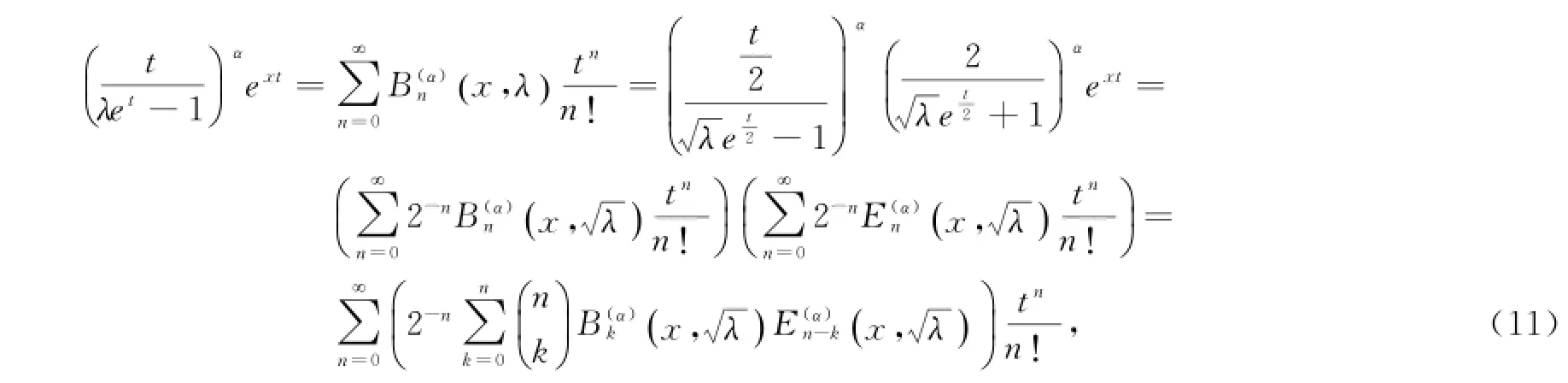
由定义2得

比较式(12)两边的系数即得式(9).

[1]王竹溪,郭敦仁．特殊函数概论[M]．北京:北京大学出版社,2004．

[2]Apostol Tom M．On the Lerch Zeta Funtion[J]．Pacific J．Maths,1951,1(1):161G167．

[3]Luo Qiuming．On the ApostolGBernoulli Polynomials[J]．Central European J．Maths．,2004,2(4):509G515．

[4]雒秋明,刘爱启．高阶Euler多项式的推广及其应用[J]．数学杂志,2006,26(5):574G578．

[5]巫朝霞,何园．关于Bernoulli多项式和Euler多项式的一个注记[J]．内蒙古师范大学学报:自然科学汉文版,2012,54(6):604G606．[6]雒秋明．Bernoulli多项式和Euler多项式的关系[J]．数学的实践与认识,2003,33(3):119G122．

[7]李志荣．广义m阶Bernoulli数和广义m阶Euler数的计算公式[J]．数学的实践与认识,2007,37(10):167G172．

[8]刘国栋．广义n阶BernoulliGEuler多项式[J]．数学的实践与认识,1999,29(3):5G10．

Combinatorial Identity of HighGorder Bernoulli Polynomial and HighGorder Euler Polynomial

Yang Cundian,Liu Duansen
(Department of Mathematics and Computational Science,Shangluo University,Shangluo 726000,China)

The relationship between the highGorder Bernoulli polynomial and highGorder Euler polynomial was researched,and the expression and the relation of the highGorder Bernoulli polynomial and highGorder Euler polynomial were acquired．Further,the identity of the classical Bernoulli polynomial and Euler polyG nomial was popularized by using the basic properties of the Bernoulli polynomial and the Euler polynomial and the elementary method．

HighGorder Bernoulli polynomial;HighGorder Euler polynomial;Identity

O156．4

A

1004G0366(2016)02G0007G03

10．16468/j．cnkii．ssn1004G0366．2016．02．002．

2015G03G23;

2015G05G21．

国家自然科学基金项目(10671155)．

杨存典(1965G),男,陕西山阳人,教授,研究方向为数论及特殊函数应用．EGmail:slycd＠126．com．