基于神经网络-模糊PID的轧机非线性扭振智能控制

韩东颖，李冰洋，时培明

（1.燕山大学 车辆与能源学院，河北 秦皇岛 066004；2.燕山大学 电气工程学院，河北 秦皇岛 066004）



基于神经网络-模糊PID的轧机非线性扭振智能控制

韩东颖1，李冰洋2，时培明2

（1.燕山大学 车辆与能源学院，河北 秦皇岛 066004；2.燕山大学 电气工程学院，河北 秦皇岛 066004）

针对轧机传动系统扭振控制问题，建立含间隙非线性的轧机系统动力学模型。考虑到轧机扭振模型的非线性和参数不易测量的特点，提出神经网络和模糊PID相结合的控制器设计方法，以模糊PID为主体，通过引入神经网络改变模糊隶属度函数的中心值和宽度，最终得到最佳PID参数。设计神经网络-模糊PID智能控制器，并利用实际轧机参数与经典双闭环控制系统进行对比仿真。仿真结果表明所设计的智能控制系统对轧机传动系统扭振的抑制作用明显优于经典双闭环控制系统。

振动与波；轧机传动系统；扭振；间隙非线性；神经网络；模糊PID

随着轧机装备水平的提高，轧机传动已由先进的交流调速取代了传统的直流调速，大大提高了轧机传动的技术性能指标。但轧机大多利用原机械设备，机械与电气配合不好，容易出现传动系统的扭振现象，引起系统动态速降，甚至破坏控制系统的稳定性。另一方面，扭振会使传动部件产生疲劳损伤，降低部件的使用寿命。剧烈的振动还会引起部件的突然破坏性断裂，造成严重的经济损失［1］。

随着现代控制理论的发展，尤其是智能控制的出现，为扭振的抑制提供了新的思路。Orlowska-Kowalska T、Kaminski M利用经过OBD技术优化的神经网络状态观测器来实现对轧机扭振的控制［2］。东北大学马庆增在滑模变结构控制的基础上引入模糊控制，实现了较为有效的扭振抑制［3］。为了实现更好的控制效果，本文提出神经网络和模糊PID控制器相结合的方法，设计了神经网络-模糊PID智能控制系统，并与经典双闭环控制系统对轧机进行对比仿真。仿真结果表明设计的智能控制系统对轧机传动系统扭振的抑制作用明显优于经典双闭环控制系统。

1　轧机传动系统的扭振模型

轧机传动系统是一个由若干惯性部件和弹性部件构成的“质量弹簧系统”。由于电机转子和轧辊的质量远大于其他部件的质量以及影响产品质量和系统动态响应品质的主要部件也是电机和轧辊，因此将轧机传动系统看成是由电动机、轧辊以及连接两者的弹性连接轴组成，也就是通常所说的轧机二质量系统，如图1所示。

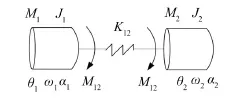
图1轧机二质量系统模型

图1中，M1是电机输出转矩；M2是轧辊负荷转矩；M12是连接轴扭矩；ω1是电机角速度；ω2是轧辊角速度；J1是电机转动惯量；J2是轧辊转动惯量；θ1是电机旋转角度；θ2是轧辊旋转角度；K12是连接轴弹性系数。

根据运动学方程式写出微分方程式得

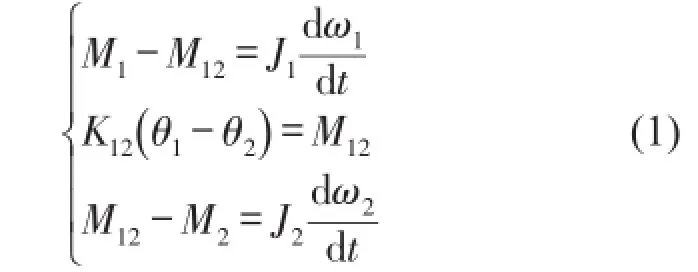
设θ1=∫ω1dt，θ2=∫ω2dt，代入式（1）得

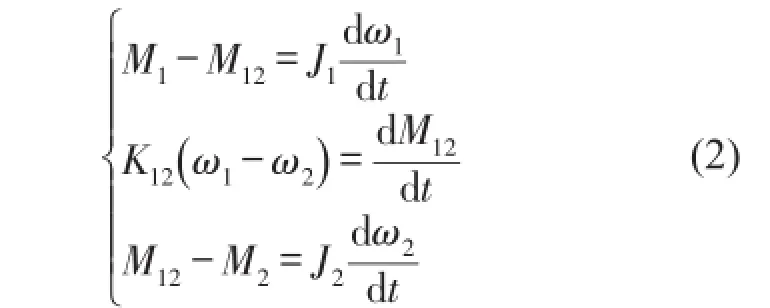
对式（2）进行拉式变换，得

从式（3）可以写出从电机转速ω1到连接轴扭矩M12的传递函数T为

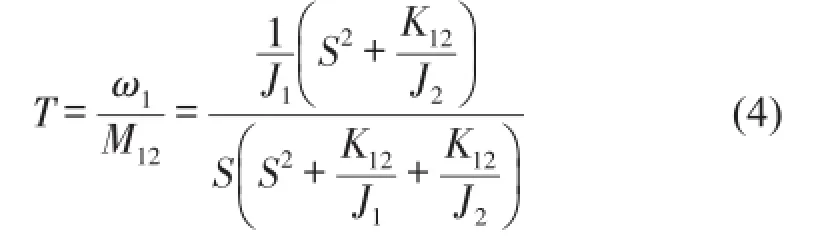
为了更贴近实际轧机，进一步建立含间隙非线性的二质量系统模型。在考虑轧机传动系统结构间隙的扭振响应计算过程中，将弹性恢复力做分段线性化处理。将分段线性弹性恢复力代入没有间隙时的扭振响应计算模型进行求解，就可得到含有间隙时的扭振响应［4］。

含间隙的轴系扭矩表示为

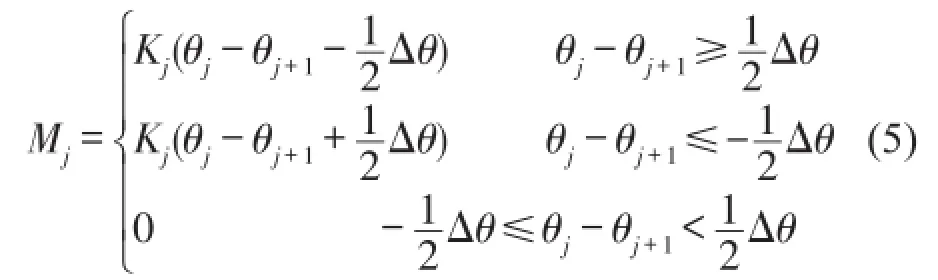
式中Kj——无间隙时的扭转刚度；

θj-θj+1——角位移；

Δθ——间隙量。

根据上式建立含间隙非线性的轧机二质量系统模型，如图2所示。

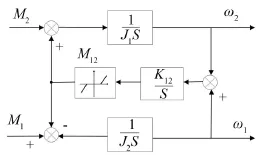
图2　含间隙轧机二质量系统框图

2　神经网络-模糊PID轧机扭振智能控制器的原理和结构

2.1控制器的原理

神经网络-模糊PID控制器是在模糊PID控制器的基础上加入神经网络［5］，也可以理解为模糊PID控制器和神经网络两部分组成了文中的神经网络-模糊PID控制器，将系统的偏差与偏差的变化率输入到神经网络中，根据预设的模糊规则控制器，输出对应于PID控制器的三个可调参数KP、KI、KD，然后控制系统对控制结果进行评价并反馈到神经网络中，经网络通过自学习与加权系数的调整，更新模糊控制的隶属度函数，直到输出最佳的PID控制参数［6］。

2.2控制器的结构

神经网络选用BP神经网络，BP模糊神经网络模型模型如图3所示，分为5层。

第一层是输入层，它的作用就是将输入值传到第二层；第二层是隶属度函数生成层，它的作用就是计算上一层的输入分向量属于本层各语言变量值的隶属度函数；第三层是模糊推理层，每个节点都对应一条模糊规则，本层要计算出每条规则的适用度；第四层是归一化层，实现的是归一化计算。第五层是精确化输出层，用来进行清晰化的计算。

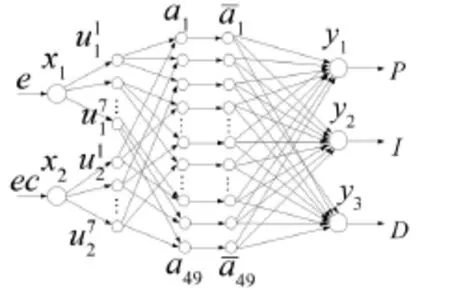
图3　控制器结构图

3　神经网络-模糊PID轧机扭振智能控制器的设计

3.1模糊PID的原理

采用由误差和误差导数组成的二维模糊控制器。模糊控制器的设计需要经历三个过程：模糊化、模糊推理和清晰化，控制原理图如图4所示。

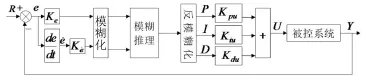
图4　模糊PID控制原理图

3.2模糊论域与隶属度函数

模糊语言变量为误差e和误差导数e˙，其论域值为［-4，4］，变量为［NB，NM，NS，ZE，PS，PM，PB］，即负大、负中、负小、零、正小、正中、正大。PID三个参数KP、KI、KD论域取［1，2］，变量为［PE，PS，PM，PB，PL］，即零、正小、正中、正大、正最大。

采用高斯型的隶属度函数，在设计时，通常在误差为零处附近的形状比较陡，以获得良好的灵敏度，而在误差大的区域则让形状较缓，以保证较强的鲁棒性。初始设定值时，令误差e和误差导数e˙的设置相同，参数KP、KI、KD的设置相同。

3.3模糊规则的确定

模糊规则是模糊模控制器的核心，其设计离不开对系统定性的分析，设计前首先要定性地给出误差与误差变化率和PID三个参数直接的关系。以阶跃信号的响应为例，给出每个阶段对应的PID参数调节要求，如图5所示。

按照误差与误差变化率的正负值和大小，可以把曲线主要分为七段，即AB、BC、CD、DE、EF、FG、GH。在AB段，e＞0，e˙＜0，其中误差是主要考虑因素，为了使误差能尽快减小以提高系统的响应时间，应给较大的P值（PL），而I和D则可以取较小的值或零（PE）。

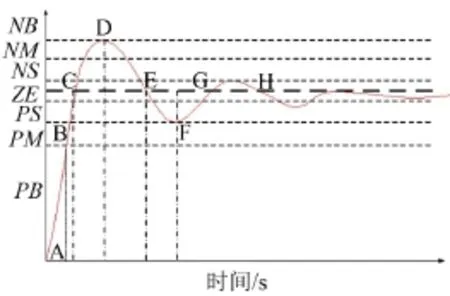
图5　阶跃响应下的系统曲线

在BC段，同样e＞0，e˙＜0，由于之前的P值较大，系统以较快的速度上升，为了减小或者避免系统的超调量，此时应该把P值减小为PB，并且随着e的减小，P值也应相应减小为PM，同时还应增大I与D的取值以减小超调。

在CD段，此时e＜0，e˙＜0，这个阶段主要目标是控制系统的超调量，使曲线快速停止上升，所以要取较大的I值（PL），同时P取适中值（PM）。

在DE段，此时e＜0，e˙＞0，这个阶段的主要目标是使曲线快速回落，并将误差控制在较小的范围。此时，P取中值（PM），I适当减小（PM），D取中大值（PM或PB）使系统有较好的抗干扰能力。

在EF段，此时e＞0，e˙＞0，为了保证稳态精度，P取中小值（PM），I取较小值（PS），D取中值（PM）。

在FG和GH段，此时e和e˙值已经接近于零，这个阶段的主要目标是精调。此时误差的积分几乎不变，因此I取零值（PE），同时P和D取较小值（PS）以保证系统的稳态精度。

根据以上的分析，可以绘制出模糊控制的规则表，误差与误差变化率的模糊子集均为7个，故共有7×7=49条规则。模糊规则如表1所示［7］。

3.4精确化输出

模糊规则确定后，开始模糊推理，求解模糊关系方程产生相应的模糊矢量。采用Takagi-Sugeno型推理，之后是将得到的模糊结果精确化，即解模糊，采用中位数法（Bisector）。最后就可以得到输入为e和e˙下的P、I、D输出。

3.5神经网络的设计和训练

神经网络的训练是在Matlab/Anfisedit中进行的，网络类型选用BP网络，分为五层［8］。训练和检测的数据从上面设计的模糊PID中提取。接着，生成模糊推理系统，完成后得到模糊神经网络的结构。训练初次生成的模糊神经网络，误差值设为0.03，训练次数为1 000次。如果训练一次达不到要求，就要对网络的进行多次训练直到达标为止。

表1　模糊推理规则表

4　基于神经网络-模糊PID轧机扭振控制系统仿真分析

仿真实验中用到的轧机参数是承钢1 780 mm板带轧机的实际参数，具体参数为：电机转动惯量J1=13×10-4kg∙m²、轧辊转动惯量J2=18×10-4kg∙m²、连接轴弹性系数K12=27 200N∙m/rad、阻尼系数ζ=0.02。模糊神经网络部分用的是上节训练完成的网络，通过编写S函数实现［9］；轧机部分用的是含间隙非线性轧机二质量系统。在0 s处加单位阶跃模拟轧机起振，在3 s处突加单位阶跃模拟轧机扭振，为了更清晰显示神经网络-模糊PID的优越性，让其跟经典双闭环控制系统进行对比，分别取连接轴扭矩和轧辊转速两个量进行比较。

（1）连接轴扭矩在训练中误差曲线如图6所示。

图7中上半部分代表的是在双闭环控制系统中连接轴扭矩仿真曲线，下半部分代表的是在神经网络-模糊PID控制系统中连接轴扭矩仿真曲线。对比上下两线可以明显看出，不论是在起振阶段还是在3 s处突加单位阶跃负载的扭振阶段，下线振荡的频率和幅度都比上线要小得多，并且下线更为平缓。

（2）轧辊转速波动在训练中误差曲线如图8所示。

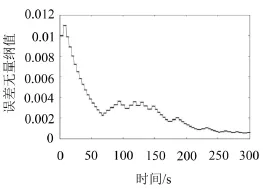
图6　连接轴扭矩在训练中均方根误差曲线

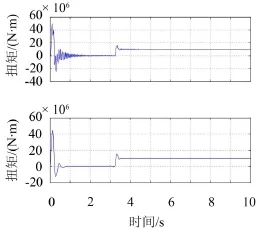
图7　连接轴扭矩对比图

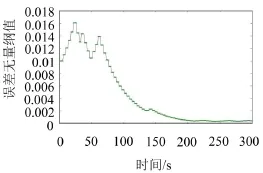
图8轧辊转速波动在训练中均方根误差曲线

图9是轧辊转速波动对比图，上图是双闭环控制系统轧辊转速波动仿真图，下图是文中神经网络-模糊PID控制系统轧辊转速波动仿真图。可见，从起振的超调量到3 s处突加单位阶跃时的动态速降，下图转速波动都比较小，并且恢复时间也短。

5　结语

通过对轧机系统的分析，建立更接近实际轧机系统的含间隙非线性轧机二质量系统模型。考虑到扭振模型比较复杂和参数不易测量的特点，建立神经网络-模糊PID轧机扭振智能控制系统。最后，为了突出该系统的优越性，让其和经典双闭环控制系统在Matlab/Simulink环境中进行对比仿真，结果表明设计的神经网络-模糊PID轧机扭振智能控制系统对轧机扭振有着更明显的抑制效果。

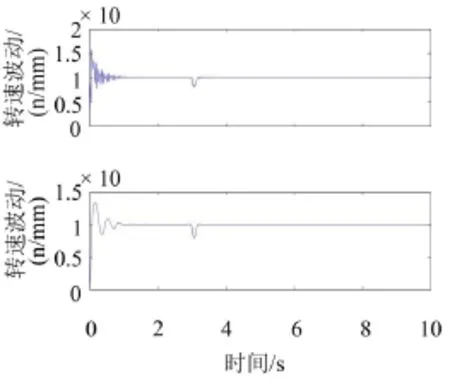
图9　轧辊转速波动对比图

［1］李崇坚，段巍.轧机传动交流调速机电振动控制［M］.北京：冶金工业出版社，2003.

［2］ORLOWSKA-KOWALSKAT，KAMINSKIM.Application of the OBD method for optimization of neural state variable estimators of the two-mass drive system［J］. Neurocomputing，2009，72:3034-3045.

［3］马庆增.轧机传动系统扭振抑制滑模变结构控制器设计［D］.东北大学，2008：43-54.

［4］侯东晓，刘彬，时培明，等.分段非线性轧机辊系系统的分岔行为研究［J］.振动与冲击，2010，29（12）：132-135.

［5］王益群，王海芳，高英杰，等.基于神经网络PID的轧机AGC力控制［J］.中国机械工程，2005，16（18）：1650-1653.

［6］SUN J，ZHANG D，LI X，et al.Smith prediction monitor AGC system based on fuzzy self-tuning PID control［J］. Journal of Iron&Steel Research International，2010，17（2）:22-26.

［7］陈志旺，李建雄，王洪瑞.模糊PI轧机位置闭环控制实验研究［J］.中国机械工程，2007，18（11）：1277-1280.

［8］贾春玉，王英华，周会锋.板形板厚综合调节神经模糊智能方法的研究［J］.中国机械工程，2003，14（20）：1741-1744.

［9］李国勇.智能控制及其Matlab实现［M］.北京：电子工业出版社，2005，194-284.

Intelligent Control of Nonlinear Torsional Vibration of Rolling Mills based on Neural Network and Fuzzy PID

HAN Dong-ying1，LI Bing-yang2，SHI Pei-ming2

（1.College of Vehicles and Energy，Yanshan University，Qinhuangdao 066004，Hebei China；2.College of Electrical Engineering，Yanshan University，Qinhuangdao 066004，Hebei China）

A dynamic model for a rolling mill with backlash nonlinearity is established for torsional vibration control analysis of the rolling mill’s drive system.Considering the nonlinearity of the model and the difficulty in parameters measurement，a controller’s design method of combining neural network with fuzzy PID is proposed.In this method，the fuzzy PID is the dominant.By introducing the neural network to adjust the central value and width of the fuzzy membership degree function，the optimal PID parameters are obtained.Then，the intelligent control system of the neural network combined with the fuzzy PID is designed and simulated using the real rolling mall parameters and the parameters of the classic double loop control system.The results show that the designed intelligent control system can suppress the torsional vibration of the rolling mill drive system obviously better than that of the classical double loop control system.

vibration and wave；transmission system of the rolling mill；torsional vibration；backlash nonlinearity；neural network；neural network；fuzzy PID

TM341；TH113.1

ADOI编码：10.3969/j.issn.1006-1335.2016.04.034

1006-1355（2016）04-0161-04+187

2016-02-25

国家自然科学基金资助项目（51005196）；河北省自然科学基金资助项目（E2012203194）

韩东颖（1978-），女，吉林省辽源市人，副教授，硕士生导师。主要研究方向为振动分析与控制、结构健康监测。E-mail:dongying.han@163.com

时培明（1979-），男，黑龙江省延寿县人，副教授，硕士生导师，主要研究方向为机械系统智能监测与控制。