坡代数的(,∨(λ,μ))-模糊理想*
2016-08-31廖祖华廖翠萃袁玩贵江南大学理学院江苏无锡24222江南大学智能系统与网络计算研究所江苏无锡2422
路 腾,廖祖华,2+,廖翠萃,2,袁玩贵,2.江南大学 理学院,江苏 无锡 24222.江南大学 智能系统与网络计算研究所,江苏 无锡 2422
路腾1,廖祖华1,2+,廖翠萃1,2,袁玩贵1,2
1.江南大学 理学院,江苏 无锡 214122
2.江南大学 智能系统与网络计算研究所,江苏 无锡 214122
LU Teng,LIAO Zuhua,LIAO Cuicui,et al.(,∨(λ,μ))-fuzzy ideals of incline algebras.Journal of Frontiers of Computer Science and Technology,2016,10(8):1191-1200.
摘要:给出了坡的(�,�∨(λ,μ))-模糊理想的概念,研究了坡的(�,�∨(λ,μ))-模糊理想的等价刻画,得到了坡的(�,�∨(λ,μ))-模糊理想在并运算与反直积运算下封闭的结论;利用反扩张原理获得了坡的(�,�∨(λ,μ))-模糊理想的同态原像与同构像的性质;最后,引入了坡的滤子的链式条件,并讨论了它的一些基本性质。坡的(�,�∨(λ,μ))-模糊理想新概念的提出扩展了坡代数理论的研究,引入的坡的滤子的链式条件的性质也可应用于其他代数结构,丰富了软代数理论研究。
关键词:(�,�∨(λ,μ))-模糊理想;滤子;链式条件;同态原像;同构像
1 引言
Rosenfeld于1971年最先提出将模糊理论应用到代数学中[1],之后有许多学者致力于代数概念的模糊化和推广。为了推广模糊子群和模糊理想的概念,Bhakat和Das在1992年至1996年期间,借助刘应明等人提出的模糊点和模糊集之间“属于”和“重于”的关系,得出了(α,β)-模糊子群的概念[2-3];袁学海等人于2003年给出了广义模糊子群的概念[4];(∈,∈∨q(λ,μ))-模糊代数是相对于Rosenfeld意义下的模糊代数,比Bhakat和Das意义模糊代数更为一般的代数结构,它由廖祖华等人于2006年提出并且他们对此进行了一系列研究工作[5-6]。
反模糊子群的概念是由Biswas于1990年首先提出[7],反模糊代数的提出是对模糊代数理论的一种扩充和发展;张成于1997年给出了(∈′,∈′∨q′)-模糊子群的定义[8];袁学海等人于2003年提出了-模糊子群的概念[9];廖祖华等人在袁学海提出的(,∨)-模糊子群概念的基础上,于2007年提出了(,∨(λ,μ))-模糊子群[10]的概念。(,∨(λ,μ))-模糊子群是一般反模糊子群和(∈′,∈′∨q′)-模糊子群的一种推广:当λ=1,μ=0时,(,∨(λ,μ))-模糊子群是一般反模糊子群,当 λ=1,μ=0.5时,(,∨(λ,μ))-模糊子群是(∈′,∈′∨q′)-模糊子群,廖祖华和他的学生们对此进行了一系列的研究[11-14]。
坡代数是由我国控制论专家曹志强于1981年提出的[15],之后他与Kim和Roush于1984年合作完成了著作[16]。Jun等人最先用模糊集的思想研究坡代数,并且于2001年定义了模糊子坡代数和模糊理想的概念,并给出了模糊子坡代数和模糊理想的若干等价条件和性质[17]。2005年,詹建明等人给出了坡的直觉模糊理想与坡的T-模糊理想的定义[18-19]。2010年,程风等人在直觉模糊集和模糊坡定义的基础上,给出了T-S模的直觉模糊坡及其理想的概念[20-21]。2011—2013年,李生刚、伏文清等人对坡进行了一系列的研究工作,得到了一些有意义的结果[22-26]。廖祖华和他的学生芮明力于2010年对模糊子坡进行了推广,给出了广义反模糊子坡的概念[27],他们又于2011年,给出了广义模糊子坡及(∈,∈∨q(λ,μ))-模糊子坡的新概念[28]。理想是代数学中的重要概念并起着重要作用,本文定义坡的(,∨(λ,μ))-模糊理想的概念并得出它的一系列基本性质。
2 预备知识
定义1[15]设K是一个非空集合,具有两种运算:加法(记为“+”)和乘法(记为“∙”,通常省略不写),对任意的x,y,z∈K满足下列条件:

则称K是一个坡。
定义2[15]设K是一个坡,K1是K的一个非空子集,若K1对于K中两种运算封闭,则称K1是K的子坡。
定义3(笛卡尔积)A、B是两个非空集合,称A×B={(x,y)|x∈A,y∈B}为A、B的笛卡尔积。
定理1[16]K1、K2是坡,在K1×K2中定义加法“+”及乘法“∙”运算:
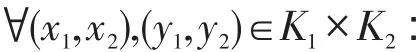
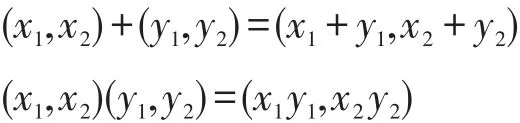
则K1×K2也是一个坡。
定义4[29]A是论域X的子集,设有如下映射:
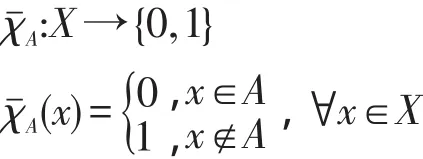
定义5[15]设K1、K2都是坡,f是K1到K2的映射,若 f满足∀x,y∈K,有:
f(xy)=f(x)f(y)
f(x+y)=f(x)+f(y)
则称 f是K1到K2的同态。若同态 f是满射,则称 f是满同态。若同态 f是单射,则称 f是单同态;若同态 f既是满射又是单射,则称 f是同构。
定义6[10]设α,λ,μ∈[0,1]且λ>μ,A是集合X的一个模糊子集,x∈X:如果A(x)<α,则称xα反属于A,记为xαA;如果α<λ且A(x)+α≤2μ,则称xα广义反重于 A,记为xα(λ,μ)A;如果xαA或xα(λ,μ)A,则记为xα∨(λ,μ)A。
定义7[27]设A∈F(K)(K上模糊集的全体),λ,μ∈[0,1]且λ>μ,若∀x,y∈K,有:
(1)A(x+y)∧λ≤A(x)∨A(y)∨μ (2)A(xy)∧λ≤A(x)∨A(y)∨μ
则称A是K的一个广义反模糊子坡。
定义8[28]设 A∈F(K),λ,μ∈[0,1]且 λ>μ,如果∀x,y∈K,若x≤y都有A(x)∨μ≥A(y)∧λ,则称A是广义逆序的。
定义9[27]设 A∈F(K),λ,μ∈[0,1]且 λ>μ,如果∀x,y∈K,若x≤y都有A(x)∧λ≥A(y)∨μ,则称A是强广义逆序的。
定义10[27]如果坡K的广义反模糊子坡A是广义逆序的,则称A是K的广义反模糊理想。
定义11[23]设K1是坡K的一个子坡,若由x∈K1, y∈K且x≤y能推出y∈K1,则称K1是K的滤子。
定义12[12](反扩张原理)设 f:X→Y为一个映射,则由该映射可以诱导出如下两个映射,分别记为与 f-1:
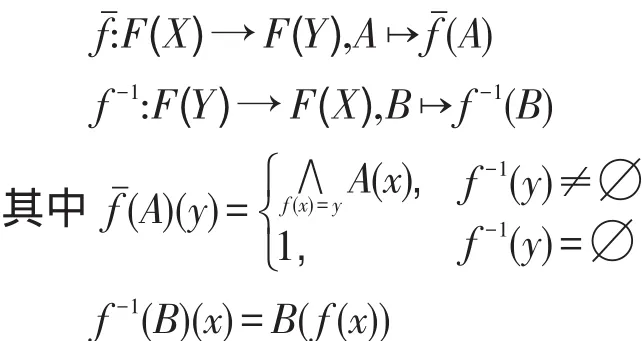
定义13设A是坡K的一个模糊集,∀x,y∈K,若x≤y,α∈[0,λ)且xαA,则yα∨(λ,μ)A,此时称A是(,∨(λ,μ))逆序的。
证明 充分性。因为∀x,y∈K,α∈[0,λ)且xαA,则A(x)<α。由于A是广义逆序的,则当x≤y时,有A(x)∨μ≥A(y)∧λ。
(1)若α≤μ,则A(y)∧λ≤A(x)∨μ≤α∨μ=μ,又因为μ<λ,所以A(y)≤μ,得A(y)+α≤μ+α≤2μ,即
(2)若 α>μ,则 A(y)∧λ≤A(x)∨μ<α,又因为α<λ,所以A(y)<α,即yαA。
必要性(反证法)。若存在x,y∈K且x≤y,此时有A(x)∨μ 取α满足A(x)∨μ<α 若yαA,则A(y)<α,与A(y)>α矛盾。 若yα(λ,μ)A,则 A(y)+α≤2μ,由 A(y)>α得2α= α+α 情形1若yμA,即A(y)<μ,与A(y)>μ矛盾。 情形2若yμ(λ,μ)A,即A(y)+μ≤2μ,因此A(y)≤μ,这仍与A(y)>μ矛盾。 综上所述,∀x,y∈K,若 x≤y,则 A(x)∨μ≥A(y)∧λ,从而A是广义逆序的。 其中0≤μ 定理3设A是坡K的一个模糊子集,则下列条件等价: (2)A是坡K的广 义反模糊理想; 假设存在x0,y0∈K,使 A(x0+y0)∧λ>A(x0)∨A(y0)∨μ,选取α满足 A(x0+y0)∧λ>α>A(x0)∨A(y0)∨μ,因此A(x0)<α,A(y0)<α,μ<α<λ且A(x0+y0)>α,从而(x0)α,(y0)αA,由已知(x0+y0)α=(x0+y0)α∨α∨(λ,μ)A。 情形1若 (x0+y0)αA,则 A(x0+y0)<α,这与A(x0+y0)>α矛盾。 情形2若(x0+y0)α(λ,μ)A,则A(x0+y0)+α≤2μ,得A(x0+y0)≤μ+(μ-α)<μ<α,这也与A(x0+y0)>α矛盾。 综上所述,∀x,y∈K,A(x+y)∧λ≤A(x)∨A(y)∨μ。 同理可证,∀x,y∈K,A(xy)∧λ≤A(x)∨A(y)∨μ。 因此,A是K的广义反模糊子坡。 (2)⇒(1):若A是K的广义反模糊子坡,∀x,y∈K,α1,α2∈[0,λ),令α=α1∨α2,如果xα1,yα2A,则A(x)< α1,A(y)<α2。 情形1如果α>μ,则 A(x+y)∧λ≤A(x)∨A(y)∨ μ<α。因为α<λ,所以A(x+y)<α,于是即 情形2如果α≤μ,则A(x+y)∧λ≤A(x)∨A(y)∨μ≤μ。因为λ>μ,所以A(x+y)≤μ,于是A(x+y)+α≤ μ+α≤μ+μ=2μ,所以 同理可证:∀x,y∈K,α1,α2∈[0,λ),如果则 (2)⇒(3):A是坡K的广义反模糊理想,则A是坡K的广义反模糊子坡,∀t∈(μ,λ],x,y∈,则A(x)≤t,A(y)≤t,A(x+y)∧λ≤A(x)∨A(y)∨μ≤t,因为t<λ,所以A(x+y)≤t,即 (3)⇒(2):假设存在x0,y0∈K,使得A(x0+y0)∧λ> A(x0)∨A(y0)∨μ,选取t满足 A(x0+y0)∧λ>t≥A(x0)∨A(y0)∨μ,故可知 A(x0)≤t,A(y0)≤t,A(x0+y0)>t且λ>t≥μ,则x0∈t且y0∈t,因为t是K的子坡,所以 (x0+y0)∈t,即 A(x0+y0)≤t,与 A(x0+y0)>t矛盾。因此∀x,y∈K,A(x+y)∧λ≤A(x)∨A(y)∨μ。 同理可证:∀x,y∈K,A(xy)∧λ≤A(x)∨A(y)∨μ。 综上所述,A是坡K的广义反模糊子坡。 假设 A不是广义逆序的,则存在 x0,y0∈K且x0≤y0,使得A(x0)∨μ (4)⇒(2):假设存在x0,y0∈R,使得 A(x0+y0)∧λ>A(x0)∨A(y0)∨μ,选取 t满足 A(x0+y0)∧λ≥t> A(x0)∨A(y0)∨μ,故 A(x0),A(y0) -t是K的子坡,所以(x0+y0)∈-t,即A(x0+y0) 同理可证:∀x,y∈K,A(xy)∧λ≤A(x)∨A(y)∨μ。 综上所述,A是坡K的广义反模糊子坡。 定理4K1是K的滤子,取两个数t1、t2满足 μ< t1<λ 证明 必要性。假设存在x0,y0∈K,使得,取,因此,由知(x0+y0)>0。由反特征函数的定义知且,因此 x0∈A,y0∈A,但 x0+ y0∉A,这与 A是K的子坡矛盾。从而∀x,y∈K,A(x+y)∧λ≤A(x)∨A(y)∨μ。 同理可证:∀x,y∈A,xy∈A。 综上所述,A是K的子坡。 综上所述,非空子集A是K的滤子。 ∀x,y∈K,α1,α2∈[0,λ),若 xα1,yα2(A⋃B),则有(A⋃B)(x)<α1且 (A⋃B)(y)<α2,即 A(x)∨B(x)<α1且A(y)∨B(y)<α2。从而 A(x)<α1,A(y)<α2,A(x)<α1,A(y)< α2,B(x)<α1且 B(y)<α2,即 xα1,yα2A且 xα1,yα2B,故(xy)α1∨α2∨(λ,μ)A且(xy)α1∨α2∨(λ,μ)B。 以下分4种情况讨论: 情形1若(xy)α1∨α2A且(xy)α1∨α2B,此时 A(xy)< α1∨α2,B(xy)<α1∨α2,从而可得 (A⋃B)(xy)=A(xy)∨B(xy)<α1∨α2,于是得(xy)α1∨α2(A⋃B)。 情形2若(xy)α1∨α2A且(xy)α1∨α2(λ,μ)B,此时A(xy)< α1∨α2且B(xy)+(α1∨α2)≤2μ。如果α1∨α2≤μ,则A(xy)+(α1∨α2)≤2μ,从而 (A(xy)∨B(xy))+(α1∨α2)≤2μ,即 (A⋃B)(xy)+(α1∨α2)≤2μ,于是得 (xy)α1∨α2(λ,μ)(A⋃B);如果α1∨α2>μ,则B(xy)≤2μ-(α1∨α2)= μ+[μ-(α1∨α2)]<μ<α1∨α2,从 而A(xy)∨B(xy)< α1∨α2,即(A⋃B)(xy)<α1∨α2,从而 综上所述,(xy)α1∨α2∨(λ,μ)(A⋃B)。 情形3 若(xy)α1∨α2(λ,μ)A且(xy)α1∨α2B,证明同情形2,有(xy)α1∨α2∨(λ,μ)(A⋃B)。 情形4若(xy)α1∨α2(λ,μ)A且(xy)α1∨α2(λ,μ)B,此时有A(xy)+(α1∨α2)≤2μ且 B(xy)+(α1∨α2)≤2μ,从而 (A (xy)∨B(xy))+(α1∨α2)≤2μ,即(A⋃B)(xy)+(α1∨α2)≤ 2μ,于是 同理可证:∀x,y∈K,α1,α2∈[0,λ),如果 xα1,yα2A⋃B,则有(x+y)α1∨α2∨(λ,μ)(A⋃B)。因此,A⋃B是坡K上的(,∨(λ,μ))-模糊子坡。 推论1设Ai∈F(K)(i=1,2,…,n)是K的(,∨(λ,μ))-模糊理想,则也是K的-模糊理想。 定义15Ai是Ki的模糊子集,i=1,2,…,n,定义映射: 则G是K1×K2×…×Kn的模糊子集,称为模糊子集A1,A2,…,An的反直积,记为 定理7若Ai是坡Ki(i=1,2)的(,∨(λ,μ))-模糊理想,则是K1×K2的(,∨(λ,μ))-模糊理想。证明因为Ai是坡Ki(i=1,2)的(,∨(λ,μ))-模糊子坡,所以 Ai是 Ki(i=1,2)的广义反模糊子坡。∀(x1,y1),(x2,y2)∈K1×K2,有: 是 K1×K2的(,∨(λ,μ))-模糊子坡。 设(x1,y1),(x2,y2)∈K1×K2且(x1,y1)≤(x2,y2),则: 推论2若Ai是坡Ki(i=1,2,…,n)的(,∨(λ,μ))-模糊理想,则是 K1×K2×…×Kn的 (,∨(λ,μ))-模糊理想。 因此,A(xy)∧λ=A(x)∨A(y)∨μ。 对任意x′,y′∈K′,因为 f是同构,所以存在唯一的x,y∈K,使得 f(x)=x′,f(y)=y′,因此 因为 f是同构,所以得 f(xy)=f(x)f(y)=x′y′,故 对任意x′,y′∈K′且x′≤y′,有x′+y′=y′,因为 f是同构,因此存在唯一的 x,y∈K,使得 f(x)=x′, f(y)=y′,因此A(y)=A(y)。由f是同构得f(x+y)=f(x)+f(y)=x′+ y′=y′=f(y),又因为 f是单射,所以 x+y=y,知x≤y。因为A是坡K的(,∨(λ,μ))-模糊理想,所以A是(,∨(λ,μ))逆序的,可知 A是广义逆序的,即A(x)∨μ≥A(y)∧λ,故 定理10设 f是坡K到坡K′的一个同态映射,B是坡K′的(,∨(λ,μ))-模糊理想,则 f-1(B)是坡K 的(,∨(λ,μ))-模糊理想。 证明 首先证 f-1(B)是坡K的(,∨(λ,μ))-模糊子坡。 同理可证:∀x,y∈K,f-1(B)(x+y)∧λ≤f-1(B)(x)∨f-1(B)(y)∨μ。 于是得到 f-1(B)是K的广义模糊子坡,由定理3 知 f-1(B)是坡K的(,∨(λ,μ))-模糊子坡。 下面证 f-1(B)是(,∨(λ,μ))逆序的即可。 综上所述,f-1(B)是坡 K的 (,∨(λ,μ))-模糊理想。 本章首先引入滤子的链式条件的概念,然后讨论滤子的链式条件与坡的(,∨(λ,μ))-模糊理想的关系。 定义16K是坡,对于K中任意滤子升链K1⊆K2⊆K3⊆…,存在正整数n,使得对所有m>n,有Km=Kn,则称K关于滤子满足升链条件。 类似的,可以定义K关于滤子满足降链条件。 定义17K是坡,对于K中任意滤子的降链K1⊇K2⊇K3⊇…,存在正整数n,使得对所有m>n,有Km=Kn,则称K关于滤子满足降链条件。 证明(反证法)若ImA⋂(μ,λ)是无限集,因为它是良序集,所以有最小元,设其为t1,因ImA⋂(μ,λ)-{t1}仍是非空集,设其最小元为t2,则t1 证明类似定理11的证明可证。 证明 假设K关于滤子不满足降链条件,则存在K的关于子坡的无穷严格降链 K1⊃K2⊃…⊃…⊃Kn⊃…。 定义模糊子集B如下: 若K=K1,则结论成立。 若K≠K1,则在K1前取K⊃K1,设此链为K⊃K1⊃K2⊃…⊃…⊃Kn⊃…。 (2)若x+y∈Kn-Kn+1,则x∉Kn+1或y∉Kn+1。不妨设 y∉Kn+1,即 y∈Km-Km+1,其中m≤n,则 B(x+y)=,因此 B(y)≤B(x)∨B(y)∨μ 综上所述,∀x,y∈K,B(x+y)∧λ≤B(x)∨B(y)∨μ。 同理可证:∀x,y∈K,B(xy)∧λ≤B(x)∨B(y)∨μ。 令x≤y,则x+y=y。 (2)若x+y∈Kn-Kn+1,则x+y∉Kn+1,可得x∉Kn+1或y∉Kn+1,若不然x∉Kn+1且y∉Kn+1,因为Kn+1是滤子,所以x+y∈Kn+1,与x+y∉Kn+1矛盾。 若x∈Kn+1,y∉Kn+1,因为x≤y,Kn+1是滤子,所以y∈Kn+1,与y∉Kn+1矛盾,因此x∉Kn+1。 若 x∉Kn+1,则存在 m 坡代数及坡代数上的矩阵理论在自动机理论、决策论、控制论、图论、神经系统等领域具有很好的应用前景。例如坡代数理论可以用于表示自动机及其他代数系统,在最优化理论中,用于研究非负矩阵的不等式及矩阵多项式等[16,30-31]。本文给出了坡的(,∨(λ,μ))-模糊理想的概念,并给出了坡的(,∨(λ,μ))-模糊理想的等价刻画及它的一系列性质。在未来的研究工作中,将探讨坡的(,∨(λ,μ))-模糊理想概念的不同刻画并研究其不同理想间是否有关联。 References: [1]Rosenfeld A.Fuzzy groups[J].Journal of Mathematical Analysis andApplications,1971,35(3):512-517. [2]Bhakat S K,Das P.On the definition of a fuzzy subgroup[J]. Fuzzy Sets and Systems,1992,51(2):235-241. [3]Bhakat S K,Das P.(∈,∈∨q)-fuzzy subgroups[J].Fuzzy Sets and Systems,1996,80(3):359-368. [4]Yuan Xuehai,Zhang Cheng,Ren Yonghong.Generalized fuzzy groups and many-valued implications[J].Fuzzy Sets and Systems,2003,138(1):205-211. [5]Liao Zuhua,Gu Hui.(∈,∈∨q(λ,μ))-fuzzy normal subgroup[J]. Fuzzy Systems and Mathsmatics,2006,20(5):47-53. [6]Zeng Junqiao,Liao Zuhua,Fan Yingying,et al.(∈,∈∨q(λ,μ))-fuzzyΓ-subrings and homomorphisms[J].Fuzzy Systems and Mathematics,2014,28(1):15-22. [7]Biswas R.Fuzzy subgroups and anti-fuzzy subgroups[J]. Fuzzy Sets and Systems,1990,35(1):121-124. [8]Zhang Cheng.(∈',∈'∨q')-fuzzy subgroup[J].Journal of Liaoning Normal University:Nature Science Edition,1997,20 (2):186-189. [9]Yuan Xuehai,Fu Yunpeng,Liu Xin,et al.-fuzzy subgroup[J].Journal of Liaoning Normal University:Nature Science Edition,2003,26(1):1-4. [10]Guo Ziyan,Liao Zuhua,Guo Jianfu.(,∨(λ,μ))-fuzzy subgroup[C]//Proceedings of the 6th International Conference on Information and Management Science,2007:570-574. [12]Hao Cuiyun,Liao Zuhua,Ji Min,et al.Some properties of(,∨(λ,μ))-fuzzy subgroups[J].Fuzzy Systems and Mathematics,2012,26(6):26-30. [13]Hao Cuiyun,Liao Zuhua.Some properties of(,∨(λ,μ))-fuzzy normal subgroups[J].Journal of Mathematics,2013, 33(5):858-864. [14]Zhu Chan,Liao Zuhua,Luo Xiaotang,et al.(,∨(λ,μ))-fuzzy complemented semirings[J].Fuzzy Systems and Mathematics,2014,26(3):54-61. [15]Cao Zhiqiang.A new algebraic system—slope[J].BUSEFAL, 1981,6:22-27. [16]Cao Zhiqiang,Kim K H,Roush F W.Incline algebra and applications[M].New York:John Wiley,1984. [17]Jun Y B,Ahn S S,Kim H S.Fuzzy subinclines(ideals)of incline algebras[J].Fuzzy Sets and Systems,2001,123(2): 217-225. [18]Ma Xueling,Zhan Jianming.Intuitionistic fuzzy ideals of incline algebras[J].Scientiae Mathematicae Japonicae,2005, 62(1):33-38. [19]Zhan Jianming,Long Ming.T-fuzzy ideals of incline algebras[J].Scientiae Mathematicae Japonicae,2005,61(1):67-73. [20]Cheng Feng,Liu Feng.T-S module’s intuitionistic fuzzy slopes [J].Fuzzy Systems and Mathematics,2010,24(S):70-72. [21]Guo Rui,Cheng Feng,Liu Feng.T-S module’s intuitionistic fuzzy quotient slopes[J].Fuzzy Systems and Mathematics, 2010,24(S):73-77. [22]Liu Lulu,Fu Wenqing,Li Shenggang.The order aspects of fuzzy subinclines,fuzzy equivalence relations,and fuzzy congruence relations[J].Fuzzy Systems and Mathematics, 2011,25(5):43-49. [23]Liu Lulu,Fu Wenqing,Li Shenggang.Characterizations of fuzzy subinclines,fuzzy ideals,fuzzy filters and fuzzy congruence relations[J].Journal of Shandong University:Natural Science,2011,46(11):48-52. [24]Zhao Hu,Li Shenggang,Chen Guixiu.Fuzzy soft subinclines in incline algebras[J].Journal of Jilin University: Natural Science,2013,51(4):555-560. [25]Fu Wenqing,Li Shenggang.Some category properties of L-ideals in inclines[J].Fuzzy Systems and Mathematics, 2013,27(6):79-85. [26]Fu Wenqing,Li Shenggang.Category of L-subinclines and its properties[J].Journal of Yunnan University:Natural Science,2013,35(2):129-136. [27]Rui Mingli,Liao Zuhua.Generalized anti-fuzzy subinclines (ideals)[J].Journal of Jiannan University:Natural Science, 2010,9(3):343-346. [28]Rui Mingli,Liao Zuhua,Hu Miaohan,et al.Generalized fuzzy subinclines and(∈,∈∨q(λ,μ))-fuzzy subinclines[J].Fuzzy Systems and Mathematics,2011,25(6):60-68. [29]Chen T Y.Lower cut set decomposition theorem and representation theorem[J].BUSEFAL,1995,63:46-48. [30]Han S C,Gu Yundong,Li Hongxing.An application of incline matrices in dynamic analysis of generalized fuzzy bidirectional associative memories[J].Fuzzy Sets and Systems,2007,158(12):1340-1347. [31]Lu Lingxia,Zhang Bei.Graphs and matroids weighted in a bounded incline algebra[J].The Scientific World Journal, 2014,Article ID 912715. 附中文参考文献: [6]曾俊俏,廖祖华,范莹莹,等.(∈,∈∨q(λ,μ))-模糊Γ-子环及同态[J].模糊系统与数学,2014,28(1):15-22. [20]程风,刘锋.T-S模的直觉模糊坡[J].模糊系统与数学, 2010,24(S):70-72. [21]郭锐,程风,刘锋.T-S模的直觉模糊商坡[J].模糊系统与数学,2010,24(S):73-77. [22]刘璐璐,伏文清,李生刚.模糊子坡代数、模糊等价关系及模糊同余关系的序方面[J].模糊系统与数学,2011,25(5): 43-49. [23]刘璐璐,伏文清,李生刚.模糊子坡代数、模糊理想、模糊滤子及模糊同余关系的刻画[J].山东大学学报:理学版, 2011,46(11):48-52. [24]赵虎,李生刚,陈桂秀.坡代数上的模糊软子坡[J].吉林大学学报:理学版,2013,51(4):555-560. [25]伏文清,李生刚.坡代数中L-理想的若干范畴性质[J].模糊系统与数学,2013,27(6):79-85. [26]伏文清,李生刚.L-子坡代数范畴及其性质[J].云南大学学报:自然科学版,2013,35(2):129-136. [27]芮明力,廖祖华.广义反模糊子坡(理想)[J].江南大学学报:自然科学版,2010,9(3):343-346. [28]芮明力,廖祖华,胡淼菡,等.广义模糊子坡与(∈,∈∨q(λ,μ))-模糊子坡[J].模糊系统与数学,2011,25(6):60-68. LU Teng was born in 1989.He is an M.S.candidate at Jiangnan University.His research interests include artificial intelligence and granular computing,etc. 路腾(1989—),男,河北石家庄人,江南大学硕士研究生,主要研究领域为模糊代数,粒计算等。 LIAO Zuhua was born in 1957.He is a professor and M.S.supervisor at Jiangnan University.His research interests include artificial intelligence and granular computing,etc. 廖祖华(1957—),男,江西奉新人,江南大学教授、硕士生导师,主要研究领域为人工智能,粒计算等。发表学术论文100多篇,主持省部级基金项目多项。 LIAO Cuicui was born in 1983.She received the Ph.D.degree from Harbin Institute of Technology in 2013.Now she is a lecturer at Jiangnan University.Her research interests include structure preserving algorithms and granular computing,etc. 廖翠萃(1983—),女,河南唐河人,2013年于哈尔滨工业大学获得博士学位,现为江南大学讲师,主要研究领域为保结构算法,粒计算等。 YUAN Wangui was born in 1974.He is a lecturer at Jiangnan University.His research interest is multi-agent system. 袁玩贵(1974—),男,安徽池州人,江南大学讲师,主要研究领域为多智能体系统。 *The National Natural Science Foundation of China under Grant No.61170121(国家自然科学基金). Received 2015-06,Accepted 2015-08. CNKI网络优先出版:2015-08-12,http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1643.009.html 文献标志码:A 中图分类号:O159 doi:10.3778/j.issn.1673-9418.1507061 LU Teng1,LIAO Zuhua1,2+,LIAO Cuicui1,2,YUAN Wangui1,2 Abstract:Firstly,this paper introduces the concept of(�,�∨(λ,μ))-fuzzy ideal of incline algebra and discusses some equivalent characterizations.Then this paper proves that the union and the anti-direct product of(�,�∨(λ,μ))-fuzzy ideals of incline algebras are still(�,�∨(λ,μ))-fuzzy ideals of incline algebras,and obtains some relative properties of its isomorphic image and homomorphic preimage based on the anti-extension principle.Finally,this paper discusses some basic properties of(�,�∨(λ,μ))-fuzzy ideals of incline algebras through the chain condition of filters of incline algebras.The new concept of(�,�∨(λ,μ))-fuzzy ideal of incline algebras expands the study of incline algebraic theory. The properties of chain condition of filters of incline algebras can also be applied to other algebraic structures,these new results enrich the soft algebra theory. Key words:(�,�∨(λ,μ))-fuzzy ideals;filters;chain condition;homomorphic preimage;isomorphic image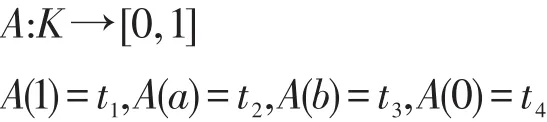
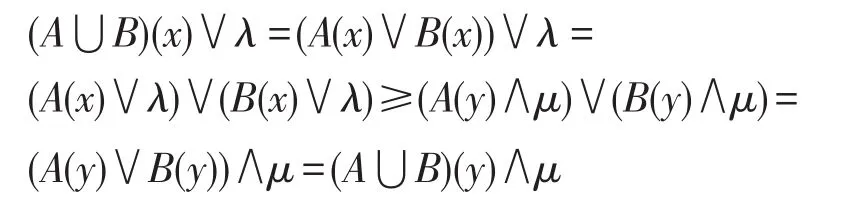
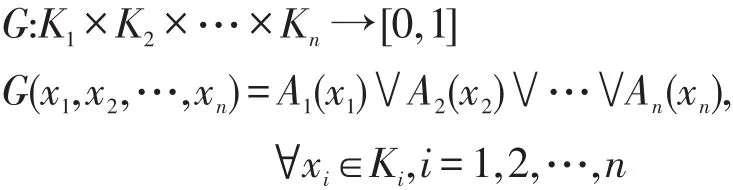

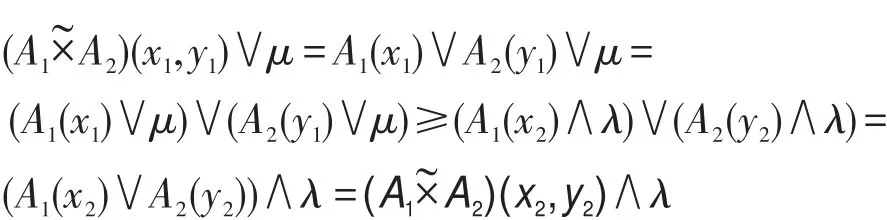
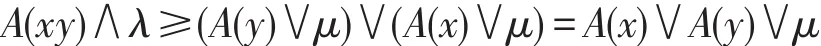
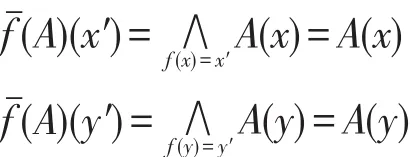
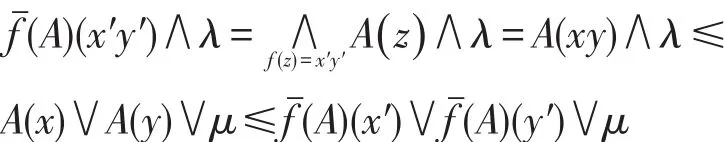
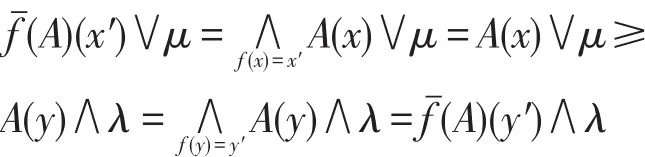
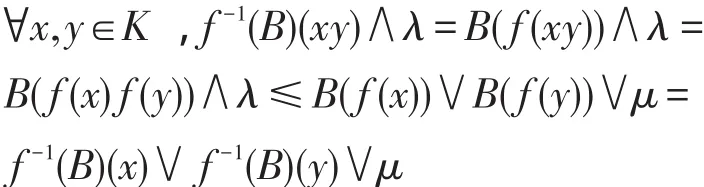
6 坡滤子的链式条件
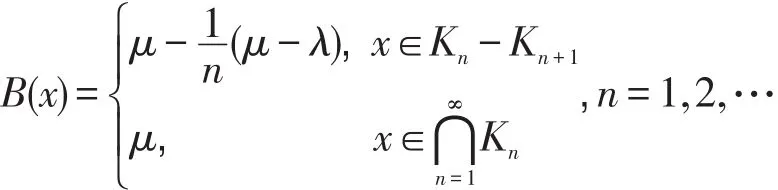
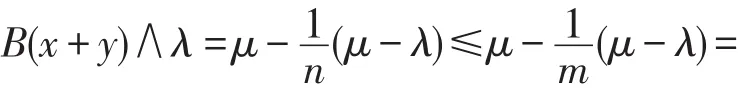
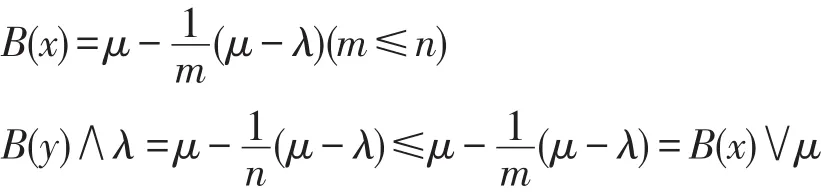
7 结束语




1.School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Institute of Intelligence System&Network Computing,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:liaozuhua57@163.com
