论平均值公理在量子力学中的地位及其对教学的启示

彭勇宜　彭　政　符力平

(中南大学物理与电子学院，湖南 长沙　410083)



论平均值公理在量子力学中的地位及其对教学的启示

彭勇宜彭政符力平

(中南大学物理与电子学院，湖南 长沙410083)

文章对平均值公理在量子力学中的作用、地位及其对量子力学教学的启示进行了详细的分析和讨论，表明只需将普通的平均值公式加以推广，便可自然地得到量子力学中的平均值公理.平均值公理在量子力学中处于基础地位，从平均值公理出发，用严格的数学理论可进一步推导出量子力学的其他基本特性.在量子力学教学过程中，从平均值公理出发，量子力学理论的逻辑和概念会更清晰，特别是对于初学者而言，这样更便于他们接受和理解量子力学理论.

平均值公理；量子力学；教学

作为物理专业四大力学之一的量子力学，其重要性是不言而喻的，可以说没有哪一门现代物理学的分支和现代高端科学技术能离开量子力学这个基础.但是，量子力学也是出了名的难学和难教的一门课程.这一方面与量子力学本身的特点有关，另一方面也与人们对量子力学的基本概念和理论体系的论述不一有关[1-4].

如何从教学的角度把量子力学教好，其中重要的一个方面就是对量子力学的理论体系作清晰的梳理，构建一个逻辑性强、便于教学的量子力学理论体系.像任何一门学科一样，量子力学理论体系有它自身发展的历史，在发展的初期过程中，有些概念并不完善，一些问题也没有彻底弄清楚，经过一段时期的发展之后，回过头来，站在一个比较高的高度重新审视它，才把整个理论看得更清楚.例如，在发展初期麦克斯韦就是用力学的方法来描述电磁场的，当时，他仿照流体力学和弹性力学的做法对电磁场作论述，给人们认识理解电磁场带来了很大的困难.但经过一个时期的发展之后，人们具备了关于场的清晰概念，再回过头来看，电磁场理论就清晰多了，不再需要用到力学的方法.量子力学也是如此，在讲述量子力学理论时，可以按照历史进程讲述量子理论，也可以不沿着发展轨迹来讲述.教学中如将量子力学的整个内容做科学的梳理，以最符合逻辑的方式重新组织量子力学理论，可以收到事半功倍的效果.

量子力学的公理体系就是将量子力学理论纳入一个逻辑体系，以公理的形式给出量子力学的基本原理，再在此基础上导出量子力学的所有内容来.这是教授量子力学最合适和最有效的一种方式[5,6].

然而，在量子力学教学的实践过程中，时常发现一些教材对公理体系的论述不一致，造成了作为初学者的学生在学习过程中的一些困惑和思维混乱.例如不同的公理之间究竟有什么关系？它们与量子力学创建初期提出的一些的基本思想，如波-粒二象性、测不准原理、叠加原理以及互补原理等究竟存在什么样的联系？它们是完全相互独立的还是在一定程度上又相互包含？这些纵横交错的疑问，往往使量子力学初学者如坠入云雾之中，造成学习和理解上的严重障碍.

本文探讨平均值公理在量子力学中的作用和地位，进而阐述其对量子力学教学的启发.多年的教学实践也表明平均值公理易于被量子力学初学者接受和理解，可以帮助他们消除上面所提到的那些疑惑，取得了满意的效果.

1　量子力学公理

任何一个物理理论都具备以下3个基本要素：①基本的物理概念；②对应的数学表示；③数学与物理概念之间的对应规则.对于量子力学初学者和讲授者而言，根据物理理论的3个基本要素，以下述公理为基础开展教学是比较合适的：

公理1： 对每一个量子体系，都存在一个复的波函数Ψ(r,t)，它描述了该量子体系在t时刻的状态.并且，所有关于该体系的信息都可从这个波函数当中获得.特别地，t时刻发现粒子在r处附近小体元d3r内的概率为

公理2： 波函数随时间的变化服从薛定谔方程

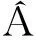
另外，还有波包收缩公理和对称化公理，由于这两条公理与本文联系不大，就不在此罗列了.

公理1给出了物理概念和相应的数学表示，即量子力学一个体系的态与表示态的数学表示：波函数.对一个体系的态的物理概念在量子力学教材中有详细的讨论，这里不再赘述.至于数学表示的波函数则意义非常清楚.公理2也没有什么争议，大家都有共识.所以，这两条公理无须作进一步讨论，大家都接受.公理3则是要讨论的重点，它是物理概念与其数学表示之间的对应规则.然而，在实际教学当中，各个教材在此问题上的提法并不完全统一.有的虽然选择这一条作为公理，可并未清楚地解释它与量子力学的新思想之间的关系，初学者感受不到它的基础地位；有的甚至就不提它，取而代之用其他的公理，形成了不同的教材采用不同的公理体系的局面，极大地影响了初学者对量子力学的认识.下面就这一公理的作用以及它与量子力学新思想之间的关系做一些论证，来说明这一公理的基础性.

2　平均值公理的地位

先看公理3的引出.根据公理1，量子体系的波函数包含了该体系的所有信息，那么，当给定一个体系的波函数后，又如何由波函数来获得某一物理量A的信息呢？也即如何由波函数求得某一物理量的可能取值和取这些值的相应概率？在经典力学当中，物理量是通过以r和p为自变量(两者表示质点的状态)的函数来表示的，所以，物理概念与数学形式之间的对应关系是清楚的.例如，一维势场中的一个质量为m的质点，其能量这一物理量就由数学公式：E=mv2/2+V(x)给出.然而，在量子力学当中，由于对体系的态定义不同，没有了类似于经典力学中的那些对应关系.此外，一个物理量的取值也不唯一，可呈现各种可能的取值，因而对这些可能的取值还存在取各值的概率的问题.因此，需要有一套能从已知状态中获得体系各物理量的可能取值以及取这些值的概率的方法.

什么样的数学形式能胜任物理量这一角色？物理量的这一数学形式与波函数(即体系的状态)的关系又是怎样的呢？先考察坐标这一物理量与波函数的关系.根据波函数的概率解释和求平均值的一般概念，可将坐标的平均值写为：

接下来考虑动量.同样，根据平均值的求法和傅里叶变换，有

可见动量的平均值与波函数的关系与前式是类似的，与前式相比，除了将动量物理量换成了算符“-i”外，两者形式完全一样.这说明其中一定存在着某种新的物理思想.再注意到，这一形式也是迄今为止所能找到的唯一表达物理量与数学形式(波函数)之间关系的式子，是实现对应规则的唯一式子.对于其他物理量情况如何呢？或一般情况下是怎样的呢？于是，像电磁学中将静磁场规律·B=0推广为时变电磁场的规律一样，将此式作推广，认为一般情况下也是成立的.这便是量子力学的第三条公理——平均值公理产生的源头.由此可见，这一条公理的出现合情合理，容易让人接受，也容易施于教学之中.

表面上看，这条平均值公式的假设非常一般，但实际上它包含着非常丰富的内容.首先，它预示着物理量必须要用算符来替代.这一点从动量平均值的计算就可以看出，即如果坚持这一平均值公式形式的正确性，则相应的动量就必须代以算符-i.此外，如果仍旧保留动能、角动量等这样一些经典物理量的概念，则可以由平均值公式确定其他物理量所对应的算符.例如，要计算动能的平均值，则由平均值的计算性质，有

因此，与动能对应的算符为

可见，对简单的力学问题来说，物理量要用算符来表示就已包含在平均值公理当中了，这时，可以不需要再将“物理量用算符表示”这条带有硬性规定似的公理单独提出.或者说，在公理体系的量子力学中，无须强调对应原理，尽管这一原理在量子力学创建初期起到非常大的作用.当然，对于更深入的量子理论，在涉及体系内部自由度问题时，由于没有经典对应，那时可以通过讲解对应原理以及对称性原理等，藉此来寻找这些无经典对应的物理量所对应的算符.但无论如何，此时的平均值公理仍然是一条可以用于检验理论与实验是否相符的重要法则.

其次，平均值公理还给出了预计测量结果的方法，即从描述体系的波函数当中获取物理量的信息，具体有如下两条推论：(1)对处于某一状态的体系，一个物理量的取值只能是表示该物理量的算符的本征值；(2)对体系的这一物理量进行测量，获得某一结果(本征值)的概率也可由平均值公理给出.这表明在整个理论体系中，平均值公理起着将理论形式与物理实际联系起来的桥梁作用.

为说明以上两条推论，先介绍概率论里的几个概念.令X为一个随机变量，取值x，ρ(x)dx为随机变量取值在[x,x+dx]区间内的概率，ρ(x)称为概率密度，或者概率分布，它是讨论随机变量统计问题的关键所在.下面给出一种确定概率密度的方法.

定义1： 随机变量X的m阶矩用〈Xm〉表示，其定义为下面的积分

由此可见，一阶矩就是平均值(期望值).

定义2： 随机变量X的特征函数定义为e-ixτ的平均值，即积分

因此，特征函数是X的概率密度ρ(x)的傅里叶变换.

将上式积分里的指数函数展开，并利用矩的定义，就有

因此，如果所有阶的矩都已知的话，则特性函数χ(τ)也就已知了，再利用傅里叶逆变换，得

即概率密度ρ(x)被确定下来了.

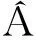
则

令ρ(a)da为物理量A取值在[a,a+da]范围内的概率，则概率密度为

因此，物理量A只有取an的概率为

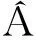
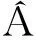
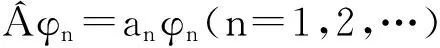
所以

从而得到物理量A的数值分布情况

上式表明：只有当a是本征值当中的数时，即a=an(n=1,2,…)，其概率才不为零，否则，a的取值概率都为零.这样，测量的可能结果只能是本征值an当中的值.第一条推论得以证明.下面计算测量获得an的概率，与前面的讨论类似，因为

即获得an的概率为|cn|2.这样，第二条推论也得以证明.

目前，许多教材将“物理量的取值为对应算符的本征值”作为公理来陈述，同时也将“测量获得某一结果的概率为|cn|2”当作另一条公理，即所谓投影假设.倘若没有平均值公理作基础，这些都很难让人一下子接受，学生往往会知其然而不知其所以然.然而，从上面的讨论来看，这些都无须当作是基本的，它们都可当作是平均值公理的产物，因此，平均值公式作为公理是理所当然的.须说明的是如果掌握了最基本的公理，再进一步学习量子力学时，为了简洁的需要可以不再用平均值公式作为公理，取而代之用其他形式的公理(比如，上面提到的投影假设)，这也是可以的.这是在理解了量子力学的基本原理、不会产生疑惑的基础上才这样做.对于量子力学初学者来讲，要很好理解和接受量子力学，用平均值公理会更合情合理些.

除此之外，从平均值这一量子力学的基本公理出发，经过一定的数学推导，还可以对在量子力学产生初期所提出的那些思想进行解释，如测不准原理.总之，有了上述提出的公理体系，可以像牛顿力学，电磁学等其他物理学学科那样，从最基本的原理出发来演绎整个量子力学，逻辑清晰而简单，从而使得量子力学的教和学变得有规可循，

不再为那些含糊不清的概念和术语所迷惑，使量子力学不再像“天书”，也不再是只停留在书本上的珍品，而是实实在在的处理实际问题的理论依据.

3　结语

平均值公理在量子力学中处于基础地位，可以由平均值公理导出量子力学中的其他特性.并且从平均值公理出发，量子力学理论的逻辑和概念变得更加简洁和清晰，特别是对于量子力学初学者而言，也更便于他们理解和接受量子力学理论.

[1]ZeilingerA.Afoundationalprincipleforquantummechanics[J].FoundationofPhysics, 1999, 29: 631-644.

[2]MullerR,WiesnerH.Teachingquantummechanicsonanintroductorylevel[J].AmericanJournalofPhysics, 2002, 70(3): 200-209.

[3]张永德.量子力学[M]. 北京: 科学出版社, 2002.

[4]邹鹏程.量子力学[M]. 北京: 高等教育出版社, 2003.

[5]Cohen-TannoudjiC,DiuB,LaloeF.Quantummechanics[M].NewYork:JohnWileyandSons, 1977.

[6]BongaartsP.QuantumTheory[M].Switzerland:SpringerInternationalPublishing, 2015.

■

DISCUSSION ON THE STATUS OF EXPECTATION VALUE AXIOM IN QUANTUM MECHANICS AND ITS ENLIGHTENMENT FOR TEACHING

Peng YongyiPeng ZhengFu Liping

(School of Physics and Electronics, Central South University, Changsha, Hunan410083)

In this paper, the effects and status of expectation value axiom (EVA) in quantum mechanics are analyzed and discussed, and its enlightenment for teaching is also analyzed. It is indicated that the EVA can be obtained naturally by extending the ordinary expectation value formula. The EVA is the fundamental quantity in quantum mechanics. According to strict mathematics theory, other basic features of quantum mechanics can be derived directly from the EVA. When the teaching of quantum mechanics starts from the EVA, the logic and concepts of quantum mechanics become more distinct. So the theory of quantum mechanics can be accepted and understood more easily, especially for beginners in quantum mechanics.

expectation value axiom; quantum mechanics; teaching

2016-01-22;

2016-03-05

2015年中南大学教学改革研究项目资助(普通教育类54号).

彭勇宜，男，副教授，主要从事近代物理学的教学与研究.pyyi@sina.com

引文格式: 彭勇宜,彭政,符力平. 论平均值公理在量子力学中的地位及其对教学的启示[J]. 物理与工程，2016，26(3)：13-17.