基于多谐振荡电路周期计算的分析

卢翠珍

基于多谐振荡电路周期计算的分析

卢翠珍

多谐振荡器是一种工作于两个暂稳态之间的无稳态电路。当电路接通电源以后，无需外加触发信号，即可在输出端得到一定频率、一定幅值的矩形波或方波。但是这一信号的周期计算公式往往都是直接给出，这不利于我们准确全面地了解多谐振荡器，为此本文将以555电路和不同系列的集成门电路构成的多谐振荡器为例，详细论述振荡周期计算公式的推导过程以解决这一难题。

多谐振荡器是一种无需外加触发信号，一旦电路接通电源以后，即可产生一定频率、一定幅值的矩形波或方波脉冲信号源。由于这种电路的结构简单，输出信号稳定。因此被广泛应用于数字电子电路中的时钟脉冲、定时控制和报警电路。但是我们在进行多谐振荡器的设计和应用时，能否得到最佳设计方案关键是振荡周期的确定，然而不管是分立元件还是集成门电路构成的多谐振荡器乃至脉冲产生电路，大多数教材和参考文献对振荡周期的计算公式都是一笔带过直接给出，这无疑不利于我们准确全面地了解多谐振荡器，同时也给设计过程带来一定的困难。因此下面将以具有实用性的555电路和集成门电路构成的多谐振荡器为例，详细论述振荡周期计算公式的推导过程以解决这一难题。

555构成的多谐振荡器周期的计算

电路组成

图1为555定时器所组成的多谐振荡电路，其结构是由数模混合的集成电路555和外接元件R1、R2、电容C两部分构成。其中虚线框部分为555定时器的内部结构，它含有两个电压比较器C1和C2、一个基本RS触发器、一个放电三极管V及缓冲器G4。比较器的参考电压由三个阻值为5kΩ的电阻构成的分压器提供，它们分别使高电平比较器C1的同相输入端和低电平比较器C2的反相输入端的参考电平为。C1与C2的输出端控制RS触发器的状态和放电开关管的状态。当输入信号自第⑥脚输入并超过时，触发器复位，555的输出端第③脚输出低电平，同时放电开关管导通；当输入信号自第②脚输入并低于时，触发器置位，555时基电路的第③脚输出高电平，同时放电开关管截止。

工作原理

假设在t=0时接通电源的瞬间，电容C来不及充电uc=0，所以高、低触发端的电平=，比较器C1输出为1，C2输出为0，即，，触发器置1，Q=1、Q-=0，使G3的输出等于0，经G4反相以后，定时器输出u0=1，放电管V截止。电容C被充电，充电回路为VccR1R2C地，充电时间常数τ=（R1+R2）C ，uc按指数规律上升，电路处于第一暂稳态。当uc上升到时，C2输出由0翻转为1，这时，触发器保持状态不变。故0＜t＜t1期间，定时器输出u0为高电平1。其工作波形如图2所示。

t=t1时刻，_uc上升到，比较器C1的输出由1变为0，这时，触发器复位为0，使Q=0、，第一暂稳态结束。

接着在t1＜t＜t2期间，因G3的输出等于1，放电管V导通，电容C开始放电。放电回路为ucR2V地，放电时间常数τ=R2C ，uc按指数规律下降，电路处于第二暂稳态。在uc下降到期间，触发器的，Q的状态保持不变，u0的状态仍为低电平。

到了t=t2时刻，uc已下降到，比较器C2输出由1变为0，，触发器置1，使第二暂稳态结束，放电管V截止，电容又被充电重复上述过程，产生振荡，在输出端得到连续的矩形波。

可见，振荡器在电容充电时，输出高电平；电容放电时，输出低电平，这样通过电容器不断地充电、放电，就能将直流形式的电能变为矩形波形式的电能。

振荡周期的计算

由工作波形图（2）可知，振荡器的振荡周期T=T1+T2，其中T1为电容充电时间，T2为电容放电时间。那么T1、T2又等于多少呢？下面我们首先来算放电时间T2：由于放电过程指的是电容C两端电压从降到，即电容充电只是充到，放电只放到时电路就发生翻转。故根据电路理论的RC一阶电路的零输入响应公式

图1 电路原理图

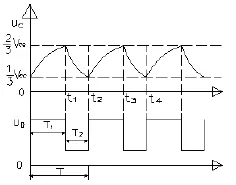
图2 工作波形图

其次电容充电时间T1实质上是电容C两端电压从Vcc升到时所需的时间，即，即电路所进行的是RC一阶电路的全响应过程，因此根据三要素法（t≥0）得：

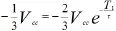
所以周期T=T1+T2=0.7（R1+R2）C+0.7R2C=0.7（R1+2R2）C

集成门电路构成的多谐振荡器周期的计算

对称式多谐振荡器

（1）电路组成及工作原理

由CMOS门电路构成的对称式多谐振荡器电路如图3所示，它是由两个反相器G1、G2和两个耦合电容C1、C2以及两个反馈电阻R1、R2组成的正反馈电路，通常令C1=C2=C，R1=R2=R。其工作过程是：假设在t=0时接通电源的瞬间，由于某种原因（扰动）使ui1有微小的正跳变，即ui1迅速跳变为高电平UOH，从而使uo1迅速跳变为低电平UOL，因电容C1的耦合作用，使ui2也迅速跳变为UOL，导致uO2迅速跳变为UOH，通过C2的作用，使ui1维持高电平，即电路发生如下正反馈过程：

电路进入第一个暂稳态。

随后uO2的高电平一方面通过R2给C1充电，如图3所示，极性左“-”右“+”另一方面通过C2、R1支门电平UTH，使uO2下跳为低电平UOL，因C2的耦合作用，ui1也跟着下跳为低电平，uo1上跳到高电平，由于C1的作用，ui2也跳为高电平，使uO2跳变为低电平，即发生如下正反馈过程：

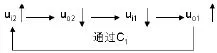
电路进入第二暂稳态。（t1～t2期间）随后uo1的高电平一方面通过R1给C2充电，如图4所示，极性左“+”右“-”使ui1上升，另一方面通过R2给C1反向充电（即C1放电）使ui2下降。在t=t2时刻，ui1上升到G1的开门电平UTH时，uO1下跳为低电平UOL，因C1的耦合作用，ui2也跟着下跳为低电平，uo2上跳到高电平，电路又进入第一个暂稳态。这样电路将在两个暂稳态之间不断地循环往复，在输出端得到矩形脉冲。其工作波形如图5所示。

（2）振荡周期的计算

从图5知振荡周期为T=tW1+tW2，而tW1和tW 2根据RC一阶电路的三要素法：（t≥0）即可求出。其中tW1为C1的充电时间，由于电容事先没有充过电，故uc（0+）=0，同时由于电容充电到开门电平时，电路发生翻转，所以某一时刻电容器两端的电压值，而电路达到稳定状态后，将它们代入上式得：经整理得：，所以有，两边取自然对数得：同理可求出C 2的充电时间

2.非对称式多谐振荡器

（1）电路组成

由TTL门电路组成的非对称式多谐振荡电路如图6所示，它是由非门G1、G2、G3和定时电路元件R、C组成，从G3输出矩形波信号。其中Rs是为避免定时电容器C反向放电时有可能造成门电路G3损坏的保护电阻。

（2）工作原理及振荡周期的计算

图3 对称式多谐振荡电路图

图4 第二暂稳态

图5 对称式多谐振荡器工作波形

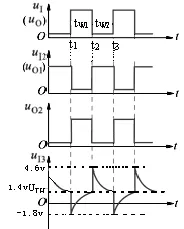
图6 非对称式多谐振荡电路图

第一个暂稳状态（t1～t2）：首先在t=t1时刻，假设ui（uo）有一个正跳变，即由0上跳到1，则uo1（ui2）由1下跳到0（即uo1的电位从3.5v变为0.3v，实际下降了3.2v。uo2由0上跳到1，根据电容C的电压不能跃变的特点知，此时的uA也由原来的1.4v下跳3.2v，则A点电位uA=1.4-3.2=-1.8v，所以这一瞬间电容两端电压uc（0+）=uA-uo1=-1.8-0.3=-2.1V ，其次uo2的高电平通过R给电容C充电，极性左“-”右“+”，结果使A点电位逐渐上升，电路进入第一暂稳态过程。在没有上升到G3的阈值电平1.4v时，G3的输出依然为高电平，uo1仍为低电平o2也为高电平，充电继续，此时电容两端充得的电压为。当经过无限长时间后，电容充电结束，其两端电压，由RC一阶电路的三要素法得：

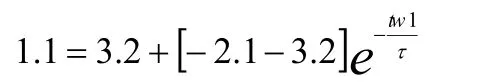
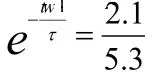
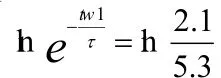
两边取自然对数

第二个暂稳状态（t2～t3）：在t=t2时刻，电容C充电到使uA=1.4V 时，G3门打开，其输出uo（ui）由高电平1跳为低电平0，电路进入第二暂稳状态。同时使uo1（ui2）由0上跳到1（即uo1的电位从0.3v变为3.5v，实际上升了3.2v）。uo2由1上跳到0，因电容C两端的电压不能突变，所以A点电位uA也将上跳3.2V，即由原来的1.4v上升3.2V，故此时的uA=1.4+3.2=4.6V，则这一瞬间电容两端电压为uc（0+）=uo1-uA=3.5-4.6=-1.1V ，随后由于uo1为高电平，uo2为低电平。uo1的高电平通过R对C进行反向充电（即电容C放电），极性左“+”右“-”，所以A点电位下降，在uA没有下降到1.4v时，G3门依然没有关闭，输出仍为低电平，uo1仍为高电平，电容C继续反向充电，A点电位继续下降，在没降到1.4v时，电容的放电过程没有结束，那么这一过程中电容两端电压：，当经过无限长时间后，电容反向充电（放电）完毕，此时电容两端电压：，故根据RC一阶电路的三要素法（t≥0）得：

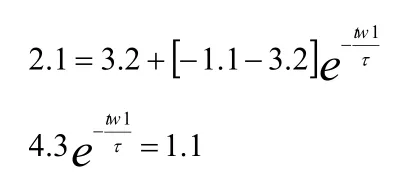
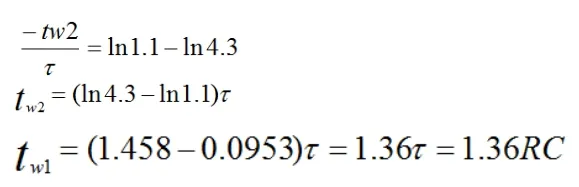
当A点电位降到1.4v时，即从t3时刻起，G3门关闭，输出高电平，反向充电结束，电路开始重复第一个暂稳态过程。这样由于电容C的充电、放电在不断地往复循环，最终在输出端uo得到连续的矩形波脉冲。

结束语：综上分析可知，多谐振荡器的工作过程实质上是通过电容器的充电、放电在两个暂稳态之间相互交替，自行产生方波或矩形波脉冲。由于方波或矩形波中含有频率丰富的高次谐波，故称为多谐振荡器。同时因多谐振荡器的工作过程不存在稳定状态，所以又叫无稳态电路。但值得注意的是，由不同系列的门电路（如CMOS 和TTL）所组成的结构不同的多谐振荡器，因其阈值电平和输出的高低电平的值不同以及充放电路径不一样，其计算周期的式子也就随之改变，因此使用时切不可生搬硬套。

DOI：10.3969/j.issn.1001-8972.2016.06.009