三轴数控机床加工误差分析*

郑　财　黄贤振

(东北大学机械工程与自动化学院，辽宁 沈阳110819)



三轴数控机床加工误差分析*

郑财黄贤振

(东北大学机械工程与自动化学院，辽宁 沈阳110819)

以三轴数控机床为研究对象，运用多体系统理论和齐次坐标变换，从装配误差、运行误差、换刀误差以及热误差这4个方面来分析数控机床加工误差，进而建立数控机床空间误差模型，分析出XYZ型数控机床的加工误差。

数控机床；多体系统理论；齐次坐标变换；误差模型

机床在机械制造工业中起到基础性的作用，是机械制造业发展的重要保证。随着科技的不断进步和创新，机械设备的加工制造工艺正朝着高精度、高效率、高稳定性的方向发展。对于一些精密仪器的加工，要求加工设备具有极其高的几何加工精度[1]。

目前，对于数控机床加工精度研究不是很成熟，大多数研究只是考虑几何误差和热误差[2-4]，同时考虑装配误差、运行误差、换刀误差以及热误差并建立综合误差模型对于数控机床加工精度的研究十分有必要。本文将XYZ型数控机床加工误差进行更深入的分析和探讨。

1　多体系统理论和齐次坐标变换

1.1多体系统理论在XYZ型数控机床中的应用

多体系统是对一般复杂机械系统的完整抽象和有效描述，是如今分析和研究复杂机械系统的最优模式。我们通过对系统的多个体进行合理的编号，然后用抽象的图行表达系统中的各个体并满足不同体之间的位置关系，来形成多体系统的拓扑结构[5]。

XYZ型数控机床的三维结构图如图1所示。

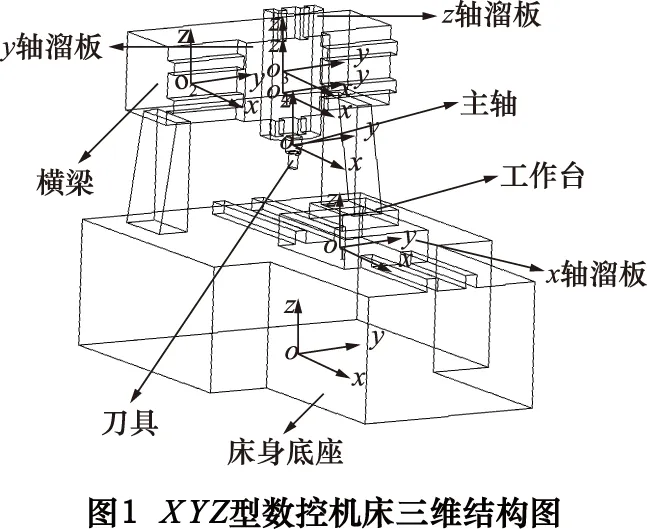
我们建立XYZ型数控机床的两条分支：工件分支和刀具分支。拓扑结构如图2所示。

根据图2所示的拓扑图，可以得到两条误差分支，即工件分支：床身—1—2；刀具分支：床身—3—4—5。

工件分支：图形1代表x溜板，图形2代表安装在x溜板上的被加工工件。

刀具分支：图像3代表y溜板，图形4代表z溜板，图形5代表刀具。

1.2齐次坐标变换理论在XYZ型数控机床中的应用

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。例如，二维点(x,y)的齐次坐标表示为(nx,ny,n)[6]。因此，一个向量的齐次表示并不是唯一确定的，齐次坐标的n取不同的值都表示的是同一个点，比如齐次坐标(16,8,2)、(8,4,1)表示的都是二维点(8,4)。齐次坐标系分析参考图如图3所示。

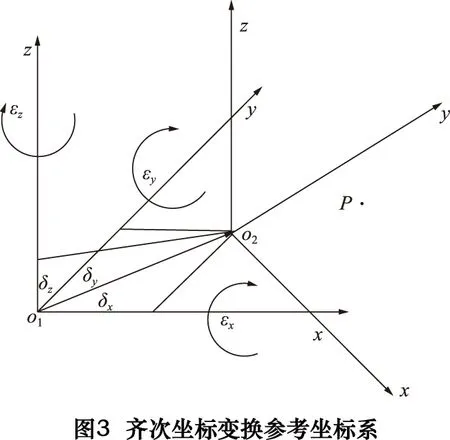
从图3所示的坐标系中可以看出，坐标系o1、o2之间存在着一定的变化关系：将坐标系o1沿x轴移动δx，沿y轴移动δy，沿z轴移动δz，平移后的坐标系再分别绕x轴、y轴以及z轴旋转角度εx、εy、εz即可得到坐标系o2。

坐标系o2到坐标系o1变换矩阵为：

T=TxTyTzRxRyRz

(1)

式中：Tx、Ty、Tz分别指坐标系o2到坐标系o1的移动坐标变换；Rx、Ry、Rz分别指坐标系o2坐到标系o1的旋转坐标变换。

当位移和旋转角度很小时，有cosε≈1、sinε≈ε，只保留一阶量并进一步化简得到：

(2)

2　XYZ型数控机床误差分析

影响数控机床加工精度的误差因素有很多，装配误差、运行误差、换刀误差以及热误差都是其影响因素。

2.1数控机床装配误差分析

我们分别在XYZ型数控机床的床身、x轴溜板、横梁、y轴溜板、z轴溜板以及主轴按如下要求建立相应的坐标系(在刀具和工件上选取的参考坐标系根据实际加工情况而定)。

(1)在机床床身上建立相应的参考坐标系，并分别在x溜板、y溜板、z溜板、工作台、横梁、主轴、刀具以及工件上建立相应坐标系。

(2)建立在x溜板、y溜板、z溜板、工作台、横梁、主轴、刀具以及工件上的坐标系的x轴、y轴以及z轴方向都要和床身底座的参考坐标系的x、y、z轴向一致。

(3)建立在x溜板、y溜板、z溜板、工作台、横梁、主轴、刀具、工件以及底座上的坐标系的坐标原点彼此之间不重合。

(4) 要在x溜板、y溜板、z溜板、工作台、横梁、主轴、刀具以及工件上选取合适的点作为装配误差计算参考点。

通过上面的分析可以得到工件误差分支的理论变换矩阵为：

(3)

但是由于实际装配误差的存在会得到工件误差分支的实际变换矩阵为：

(4)

式中：

(5)

(6)

(7)

式中：x、y、z代指相邻部件参考位置点间的理论坐标差值；Δx、Δy、Δz是相邻部件参考位置点间的移动误差差值；εx、εy、εz指旋转误差差值。

同理可得到刀具误差分支的实际变换矩阵：

(8)

T(实际)=T(理论)·E

(9)

式中：E是一个综合误差矩阵。

(10)

由于计算量较复杂，可以将工件分支和刀具分支的装配误差矩阵的表达式简化为式(11)和(12)。

(11)

(12)

可以将总的装配误差定义为：

E(装配)=E(工件)⊕E(刀具)

(13)

式中：⊕代表只把矩阵中含有字母的对应项相加，常数项不相加。

2.2数控机床运行误差分析

根们据XYZ型机床的特点，按下面的要求建立数控机床的不同参考坐标系。

(1)在们机床床身上建立参考坐标系o，并分别建立x溜板、y溜板、z溜板、刀具以及工件的参考坐标系o1、o2、o3、T和M。

(2)x溜板、y溜板以及z溜板建立的参考坐标系的x轴、y轴以及z轴方向都要和床身底座的参考坐标系的x、y、z轴向一致。

(3)建立在刀具和被加工工件上的坐标系的x轴、y轴以及z轴方向都要和床身底座的参考坐标系的x、y、z轴向一致。

(4)根据XTYZ型机床的结构特点，在数控机床床身的合适位置选取床身底座的坐标原点。

(5)x溜板、y溜板以及z溜板建立的参考坐标系的原点o1、o2、o3和参考坐标系o的原点重合。

(6)为了便于分析，刀具和加工工件的参考坐标系的原点需要单独建立：在刀尖处建立刀具坐标系原点，在工件底部处建立工件坐标系原点。

刀具运动链：机床床身—y溜板—z溜板—刀具，以及工件运动链：机床床身—x溜板—安装在x溜板上的被加工工件。

在理想状态下也就是几何误差不存在的情况下，刀具的实际切削点应该和编程所指示位置重合[7]，此时刀具坐标系T相对于工件坐标系W的坐标变换矩阵为：

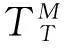
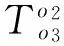
(14)

在实际加工过程中，刀具的实际切削点和理论位置会发生一定的偏移，此时刀具坐标系T相对于工件坐标系W的坐标变换矩阵为：

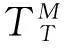
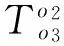
(15)

进一步分析得：

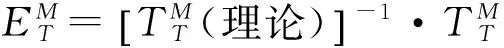
(16)

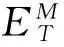
(17)

式中：Δδx、Δδy、Δδz为刀具坐标系相对于工件坐标系的位置误差：Δθx、Δθy、Δθz为刀具坐标系相对于工件坐标系的旋转误差。

将不同运动链的具体的坐标变换矩阵代入后可得Δδx、Δδy、Δδz和Δθx、Δθy、Δθz的具体表达式。

2.3数控机床换刀误差分析

由于数控机床在加工过程中换刀的次数与具体加工的工件有关，因此可以假设数控机床的换刀次数为n。为了便于计算，在选取合适的参考坐标系后，可以直接分析换刀一次后刀尖理想位置和实际位置的偏差。假设Δx1、Δx2、Δx3、…、Δxn为换刀后x方向的偏差，下标字母代表换刀的次数；Δy1、Δy2、Δy3、…、Δyn为换刀后y方向的偏差，下标字母代表换刀的次数；Δz1、Δz2、Δz3、…、Δzn为换刀后z方向的偏差，下标字母代表换刀的次数。

换刀n次后x轴方向总的偏移量为：

(18)

换刀n次后y轴方向的总的偏移量为：

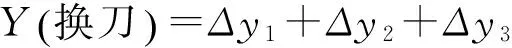
(19)

换刀n次后z轴方向的总的偏移量为：

(20)

(21)

2.4数控机床热误差分析

数控机床在加工过程中，由于加工时机床零部件间温度的升高，除了几何误差外，还会产生热误差。当溜板沿某一轴向运动时，由于热转动误差较小一般可以忽略，所以只考虑热漂移误差[8]。

当数控机床的溜板沿x轴、y轴以及z轴中的某一轴运动时，会产生3个不同方向的热漂移误差，具体可以做以下规定：

(1)当溜板沿x轴移动时，产生的热漂移误差分别为lx(x)、ly(x)、lz(x)。

(2)当溜板沿y轴移动时，产生的热漂移误差分别为lx(y)、ly(y)、lz(y)。

(3)当溜板沿z轴移动时，产生的热漂移误差分别为lx(z)、ly(z)、lz(z)。

其中，下标字母x、y、z代表热漂移误差的方向,括号内的字母代表溜板的移动方向。

当数控机床在高速转动时，主轴虽然会产生大量的热量，但由于数控机床的安装精度以及材质要求较高，在这里也只考虑主轴的3个热漂移误差，分别记为：lx(主)、ly(主)、lz(主)。

同样从工件分支和刀具分支来对数控机床进行热误差的坐标变换。工件分支：床身—1—2；刀具分支：床身—3—4—5。

工件分支：图形1代表x溜板，图形2代表安装在x溜板上的被加工工件。

刀具分支：图像3代表y溜板，图形4代表z溜板，图形5代表刀具。

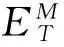
(22)

式中：

(23)

Δly=ly(x)+ly(y)+ly(z)+ly(主)

(24)

Δlz=lz(x)+lz(y)+lz(z)+lz(主)

(25)

3　结语

我们将数控机床误差分为装配误差、运行误差、换刀误差以及热误差这四项误差。为了便于分析，可以假设这四项误差相互独立，那么数控机床的综合误差就是这四项误差之和。

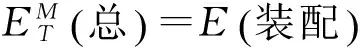
(26)

[1]袁哲俊. 精密和超精密加工技术[M].北京: 机械工业出版社, 2007:1-9.

[2]岳中军.五轴数控机床通用几何误差软件补偿技术的研究[D].北京:北京工业大学，2005.

[3]张志飞.多轴数控机床热误差与几何误差建模及补偿技术的研究[D].天津：天津大学，2000.

[4]童恒超, 杨建国. 数控车床两轴联动系统空间误差建模技术[J].上海交通大学学报,2006, 40(7): 1213-1217.

[5]王秀山,杨建国,闫嘉钰. 基于多体系统理论的五轴机床综合误差建模技术[J]. 上海交通大学学报, 2008,42(5): 761-764.

[6] 童恒超, 杨建国. 机床导轨系统空间误差的齐次变换建模及应用[J].上海交通大学学报, 2005, 39(9): 1400-1403.

[7]王哲,赵爱国,赵德云，等.数控机床定位精度的综合分析[J]. 机械设计与制造, 2010(9): 132-133.

[8]刘延斌,韩秀英. 双转台五轴数控机床的综合误差建模与补偿研究[J]. 机床与液压,2008,36(4): 241-243.

(编辑谭弘颖)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Three axis NC machine tool machining error analysis

ZHENG Cai，HUANG Zhenxian

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, CHN)

Based on the three axis NC machine tool as the research object, using the multi-body system theory and homogeneous coordinate transformation, from the four aspects of assembly error, error operation，tool change error and thermal error to analyze NC machine tool machining error, and the numerical control machine tool space error model, theXYZtype NC machine tool machining error.

NC machine tool；multi-body system theory；homogeneous coordinate transformation；error model

TH161.5

A

10.19287/j.cnki.1005-2402.2016.08.014

郑财，男，1990年生，硕士研究生，从事机械可靠性设计研究。

2016-01-05)

160825

* 国家自然科学基金项目(51105062&51305071)