梯形永磁体盘式无铁心电机的设计与研究
2016-08-30谢颖曲春梅
谢颖, 曲春梅
(哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080)
梯形永磁体盘式无铁心电机的设计与研究
谢颖,曲春梅
(哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080)
针对永磁盘式无铁心同步电机的轴向磁场结构,在现有Halbach永磁阵列的基础上,提出一种梯形结构永磁体阵列。详细阐述该电机的结构与优点,利用有限元方法研究了不同梯形结构永磁体阵列对气隙磁密的影响,根据气隙磁场中的谐波含量及空载反电势畸变率选取最优转子结构。该结构在保证与传统结构永磁体材料用量相当的前提下,有效提高气隙磁密的基波,降低谐波含量。由于轴向磁场结构的特殊性,给出该电机的设计规则,如磁极尺寸和导体占空比的确定。计算了电机在负载工况下不同定子电流对交直轴电感的影响,为该类电机的设计提供了一定的参考价值。
盘式无铁心电机;Halbach阵列;梯形永磁体;有限元方法;气隙磁密
0 引 言
盘式永磁同步电动机(简称盘式电机)的气隙是平面的,气隙磁场是轴向的,其作为一种特殊结构的永磁同步电机,结合了永磁同步电机和轴向磁通电机的特点,具有轴向尺寸短、质量轻、体积小、结构紧凑等优点,受到人们越来越多的关注[1-4]。尤其在轴向尺寸有限的应用场合,如电动汽车、手持电动工具、机械臂、船用推进器等,具有明显优越性。目前已有不少关于轴向磁场无铁心永磁电机方面的研究[5-10],该类电机是由双转子和单定子组成双气隙对称结构,不需要利用中间定子铁心来形成闭合回路,即形成轴向磁场无铁心永磁电机。该结构能够减小电机质量,消除齿槽转矩和铁心损耗,但其定子采用无铁心后,导致电机的转矩密度比较低[11]。
永磁电机设计中,永磁体多采用径向或切向阵列结构,Halbach永磁体阵列是将径向与切向阵列结合在一起,合成的结果使一侧的磁场增强而另一侧的磁场减弱[12]。Halbach阵列的磁屏蔽功能可有效提高气隙磁密基波幅值,并可获得更接近正弦分布的气隙磁密波形[13-14]。国内外文献关于无铁心永磁电机采用Halbach阵列的报道很多,其中文献[15]中应用于太阳能电车上的盘式永磁直流电机,采用Halbach阵列后既提高了电机的效率,又减轻了电机重量,使太阳能电车的整体性能得到了提高。文献[16]中提到为了克服单边磁拉力和减少漏磁采用双外转子结构,可有效提高力能密度。
结合Halbach阵列的优点,本文提出了一种梯形永磁体结构的盘式无铁心电机,研究了不同梯形结构对气隙磁场及空载反电势畸变率的影响,最终确定最优结构,该结构可提高气隙磁密基波,削弱三次谐波含量,减少永磁体的用量,降低电机成本,但是增加了工艺难度。针对该类结构电机,本文研究了开域磁场的简化问题,计算了负载情况下定子绕组的交直轴电感,对该类电机的设计有一定的参考价值。
1 梯形结构永磁盘式无铁心电机的结构特点
基于Halbach阵列梯形永磁体结构盘式无铁心电机的结构如图1所示。该电机包括无铁心楔形定子绕组盘、位于定子绕组盘两侧的对称的永磁体转子盘,以及高机械强度、非磁性材料所构成的转子外壳。楔形定子盘由绕组注塑而成,转子永磁体采用具有高矫顽力、高剩磁密度的钕铁硼材料,将永磁体直接粘到外壳上,避免了永磁体和外壳相互运动产生的涡流损耗。梯形永磁体结构盘式无铁心电机三维有限元分析模型如图2所示,图中永磁体径向截面呈梯形和矩形交替排列。
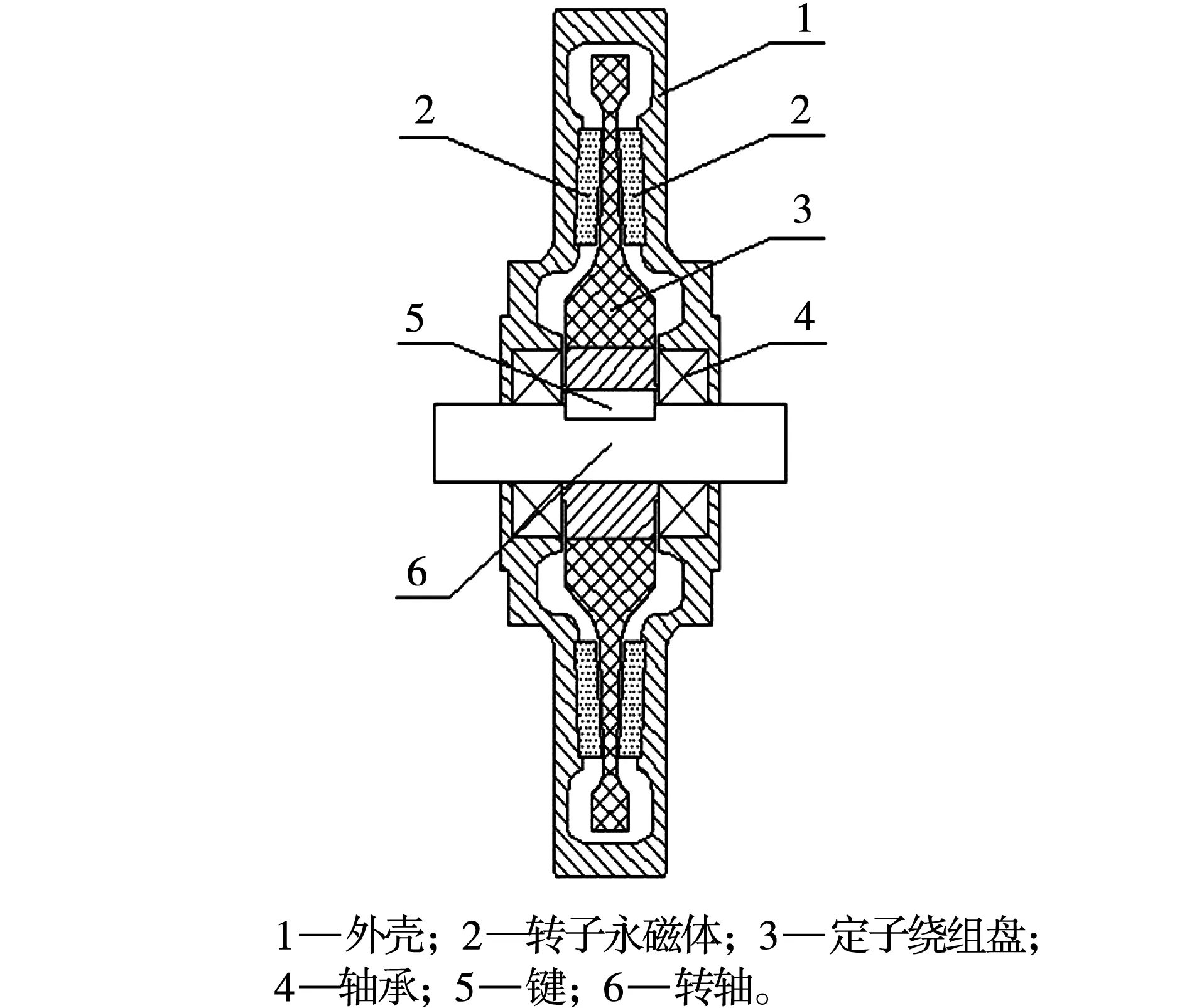
图1 梯形永磁体盘式无铁心电机结构Fig.1 Structure of trapezoidal permanent magnet disc coreless motor

图2 3D有限元分析模型Fig.2 3D FEA model
采用45°Halbach永磁阵列,各永磁体对应的充磁方向如图3所示,对于Halbach型永磁体阵列,磁钢每极由主磁极和辅助磁极构成,由于辅助磁极对主磁极有补偿作用,气隙磁场波形会根据辅助磁极的贡献大小出现平顶或马鞍形,而气隙磁密的幅值主要取决于主磁极的贡献,其中图3中90°充磁方向的永磁体为主磁极,其余永磁体为辅助磁极。无铁心盘式电机采用梯形永磁体结构有如下显著优点:
1)定子、转子盘均采用无铁心结构,电机无齿无槽,消除了齿槽转矩与铁心损耗的影响,提高电机效率。
2)梯形永磁体结构电机在提高气隙磁密基波幅值的基础上,削弱谐波含量。
3)梯形结构永磁体盘式电机与传统结构电机相比,永磁体用量减少,减轻了转子重量,降低了电机成本。
4)该结构电机在直轴电流大于0时,产生的磁场与永磁体产生的磁场方向一致,增加了永磁体磁场,可在一定程度上提高电磁转矩。
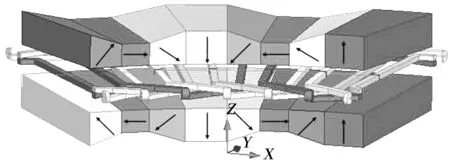
图3 永磁体转子充磁方向Fig.3 Magnetizing direction of permanent magnet rotor
2 梯形永磁体盘式电机设计与分析
2.1电机参数与方程
研究盘式永磁电机主要参数如表1所示,利用有限元软件对该电机进行电磁场分析,磁矢量位方程如式(1)所示,该模型忽略定转子涡流损耗。

表1 电机设计参数
(1)
式中:Az为磁矢量位在z方向上的分量;Jz为源电流密度在z方向上的分量;μ为磁导率;σ为材料的电导率;Γ1为电机磁场模型的边界。
2.2内外径的选取
电机的外形尺寸需满足安装要求,然后满足输出功率最大的要求。当电机外径Dout给定时,可以通过确定几何尺寸比γ来获得盘式电机最大输出功率[17-18]。由于盘式永磁电机绕组在内径处导线密集,电负荷最大,如果此处电负荷过高,会引起电枢绕组局部过热,同时综合考虑电机用铜量、效率、漏磁等因素,因此选取几何尺寸比为1.5,计算公式如下:

(2)
式中:Dout为盘式永磁电动机永磁体盘的外径;Din为永磁体盘的内径;γ近似等于电枢外径与内径之比。
2.3导体占空比
设计的盘式无铁心永磁同步电机无齿无槽,并采用楔形气隙结构,相对于传统电机中的槽满率,本设计中以导体占空比代替槽满率,方程如下:
S=S1/S2。
(3)
式中:S表示导体占空比;S1表示某一半径处导体截面积总和;S2表示某一半径处绕组空间的截面积。由于绕组盘厚度不同,因此内外径处的导体占空比计算公式如下:
(4)
由于电机绕组匝数一样,如果是均匀气隙结构,则内径和外径处的导体占空比差异很大。因此,为了充分利用外径的空间,采用楔形气隙结构,即将内外径处的导体占空比设计成相同值,则在外径处的气隙就应相应变小,整个电机的等效气隙也相应变小,有利于电机力能指标的提高。
3 永磁盘式无铁心电机优化设计
3.1开域磁场简化研究
因其盘式电机的特殊结构,其电机内部磁场分布与一般圆柱式电机差别较大,在分析其磁场分布时一般需要做三维分析。为了节约时间和有效利用计算机资源本文只针对1/8周期模型进行研究,三维有限元周期模型如图4所示。
采用有限元法对开域磁场进行计算时,必须将开域的无限区域变成有限元法可用的有限区域,使用足够大的外围区域来代替开域部分,因此选择空气罩。对于选取空气罩尺寸,选太大的求解域精确度虽高,但计算工作量太大;选择太小的求解域又难以保证精度。通过选取不同的空气罩尺寸来分析比较,确定合适的求解域来解决问题。采用空气域轴向(沿z轴方向)长度与电机轴向长度的比值作为变量,得到磁密峰值随空气罩尺寸变化趋势如图5所示。

图4 周期模型空气域Fig.4 Air region of periodic model

图5 空气域尺寸对气隙磁密影响Fig.5 Influence of air domain size on the air gap flux density
当空气域尺寸为电机尺寸3.5倍以上时,盘式电机平均半径处沿周向的气隙磁密峰值的变化趋势基本是一条直线。当空气域尺寸为电机尺寸3.5倍以上时,电机内磁场分布的计算结果就不会产生太大差异,而空气域外围认为是等零磁位面,简化了三维开域磁场问题,采用空气域半径为电机尺寸的4.5倍进行建模。
3.2梯形永磁体结构优化研究
双转子永磁盘式电机的上下两个转子盘空间对称,因此只针对上层永磁体结构进行分析。Halbach永磁阵列电机的气隙磁密幅值主要取决于主磁极的贡献,图6周期模型中1号、5号、9号、13号永磁体为主磁极,其他永磁体为辅助磁极,因此合理增加主磁极的厚度,优化辅助磁极结构,可达到提高气隙磁密的目的。图7是单个永磁体结构图,每个永磁体沿轴向的投影均为扇形,α为永磁体的旋转角度即宽度,Rin为永磁体内半径,L为永磁体径向长度。
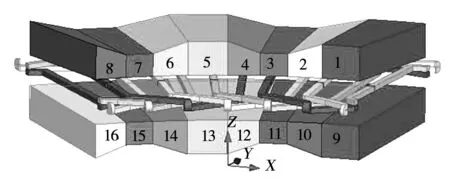
图6 梯形永磁体结构Fig.6 Trapezoidal permanent magnet structure
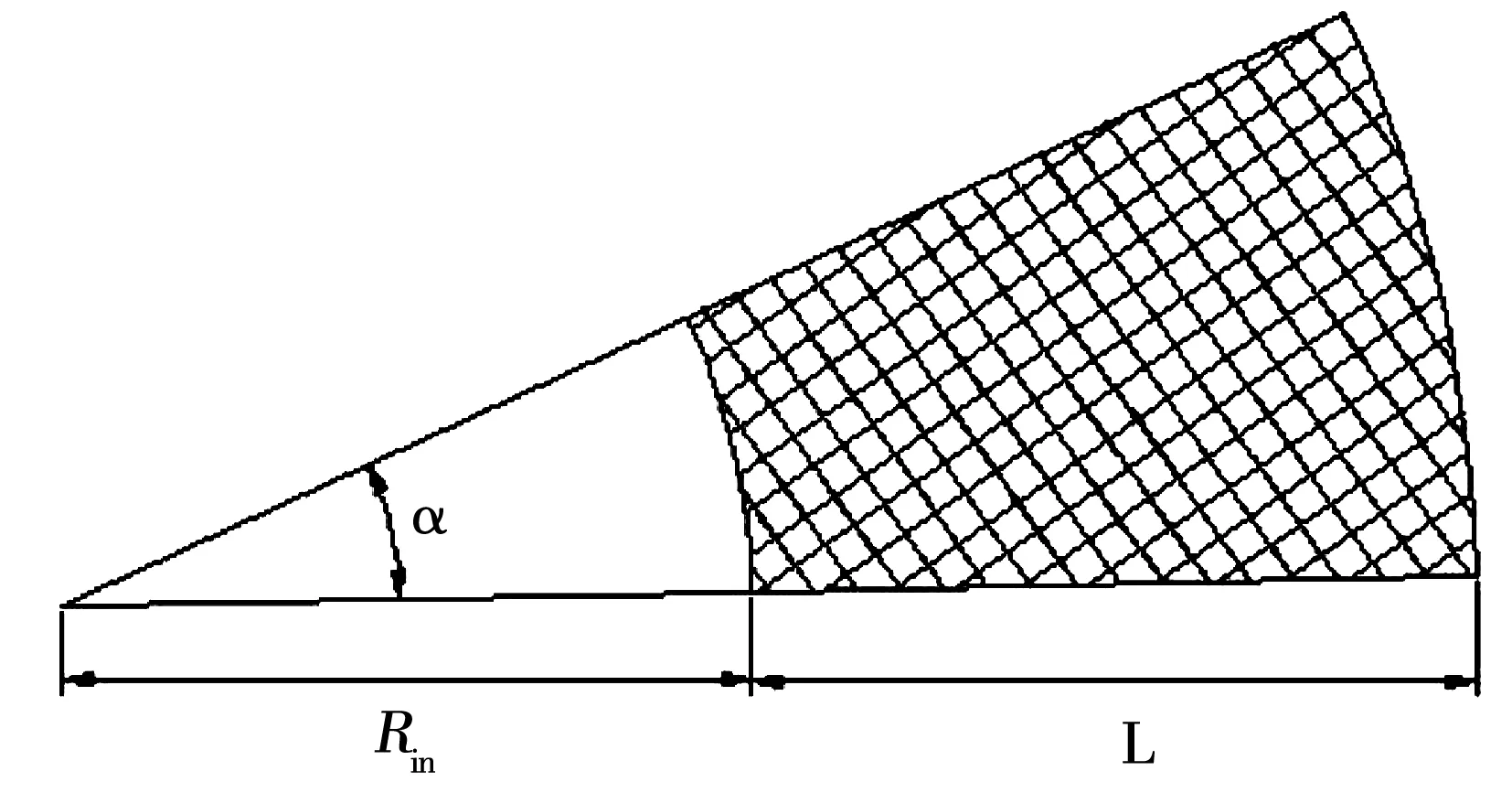
图7 单个永磁体结构Fig.7 Single permanent magnet structure
针对梯形永磁体结构有多种组合形式,表2中给出了其中五种结构,表中1号、5号永磁体厚6 mm,3号、7号永磁体厚4 mm,其余永磁体尺寸由相邻永磁体结构决定。分析这五种永磁体结构电机在空载情况下的气隙磁密分布规律,并计算各结构空载反电势波形的畸变率,永磁同步电机中空载反电势是一个非常重要的参数,由电机中永磁体产生的空载气隙基波磁通在电枢绕组中感应产生,与气隙磁通密切相关,根据规定空载反电势畸变率的值不能超过5%,因此可将其作为判断结构优劣的标准。
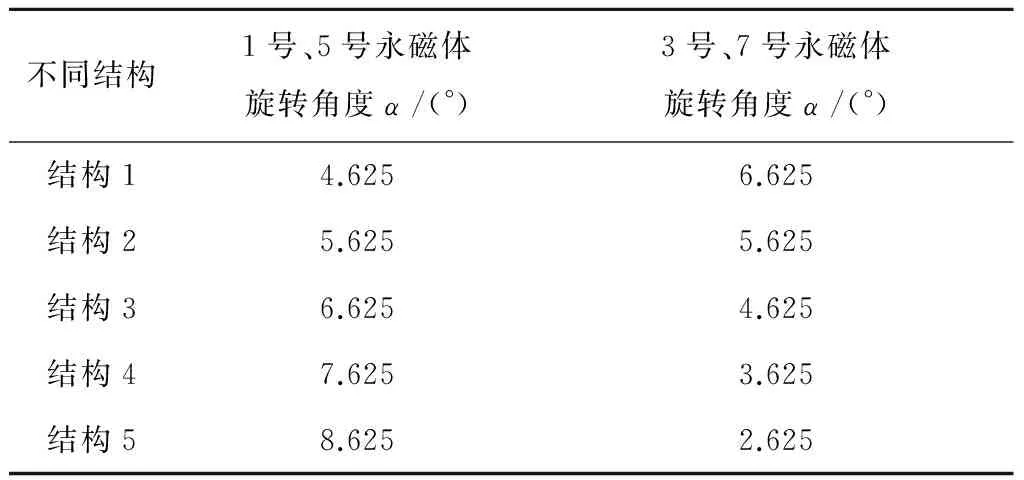
表2 各结构永磁体旋转角度
五种永磁体结构电机的气隙磁密波形如图8所示,由图可知结构1、结构2、结构3的气隙磁密接近正弦波,且1号、5号永磁体越宽波顶处越平缓,幅值越小。对气隙磁密进行FFT分解,得到的各次谐波情况如图9所示,结构3的基波幅值最大,其值为0.79T,而且各次谐波含量较低,特别是三次谐波含量与其他结构相比最小。图10是各结构空载反电势波形畸变率,从该图变化趋势来看结构3的值最小,因此将结构3视为最优结构。

图8 各结构气隙磁密分布Fig.8 Distribution of gap flux density with different structures

图9 各结构气隙磁密谐波含量Fig.9 Harmonic content of air gap flux density with different structures
基于传统等厚结构永磁体提出了梯形永磁体结构,这种梯形组合式结构的磁场与每个永磁体的尺寸大小相关,图6中1号、5号、9号、13号永磁体越宽,基波幅值先增大再减小,在谐波含量方面3次谐波含量变化明显,呈先减少再增大趋势。
3.3梯形结构永磁体与传统结构的对比
通常,Halbach永磁阵列中各永磁体是等厚的,这种结构虽然加工方便,但是不能有效提高气隙磁密,因此将永磁体用量相当的三种结构进行对比,它们分别是等厚5 mm永磁体结构,如图11所示;由4、5、6 mm组合形成的不等厚结构,如图12所示以及梯形永磁体结构3。

图10 各结构空载反电势畸变率Fig.10 No-load back EMF distortion rate with different structures

图11 等厚5 mm永磁体转子结构Fig.11 Equal thickness of 5mm permanent magnet rotor structure

图12 不等厚永磁体转子结构Fig.12 Unequal thickness of permanent magnet rotor structure
通过计算上述三种结构的气隙磁场,得到如图13所示的气隙磁密分布波形,由图可知,三种结构的波形很接近.它们的FFT分解情况及空载反电势畸变率如图14、图15所示,从图中可以发现,三种结构中梯形结构的基波幅值最大,3次、5次谐波含量均比其他两种结构小,将梯形结构各参量的值与其他两种结构做差,再将差值除以梯形结构的参数值,得到的梯形结构3与其他两种结构相比各参量变化的百分比如表3所示。由表3可知,梯形永磁体结构在不增加材料的基础上气隙磁密的基波含量相比与其他两种结构分别提高了5.37%和4.92%,同时减小了谐波含量,提高了电机的性能指标。

图13 各结构气隙磁密分布Fig.13 Distribution of air gap flux density with different structures

图14 各结构气隙磁密谐波含量Fig.14 Harmonic content of air gap flux density with different structures

%
永磁盘式电机采用45°充磁方式后,90°和270°充磁方向永磁体视为主磁极,其他充磁方向视为辅助磁极。理论上每极永磁体块数越多,气隙磁密波形正弦性越好,采用不等厚结构后,虽然有效提高了气隙磁密基波含量,但是谐波含量也增加,这是因为不等厚永磁体之间存在高度差,导致谐波含量增加,而梯形结构可有效缓解高度差问题,在提高气隙磁密基波幅值基础上减少谐波含量。

图15 各结构空载反电势畸变率Fig.15 No-load back EMF distortion rate with different structures
4 梯形永磁体结构盘式电机电感分析
4.1交直轴电感的计算
交直轴电感是永磁盘式电机的重要参数,传统结构盘式电机交直轴电感相同,而梯形永磁体结构电机的磁路磁导不一致,导致dq轴电感是不相等的,因此对该结构的电感进行分析尤为重要。在有限元中分析永磁同步电机交直轴电感时,需要对电机的三相绕组施加交直轴电流,在永磁同步电机的矢量控制中,假设将空间矢量由ABC轴系先变换到静止的DQ轴系再变换到同步旋转dq轴系[19-20],则

(5)
式中:θ为电机转子直轴与A相绕组轴线夹角;电机三相电流用id、iq表示的表达式为

(6)
电机的交直轴电流和定子电流存在下面的关系:
(7)
式中:ie为电机定子电流;β为iq与ie的夹角。将式(7)代入式(6)得电机三相电流的表达式如下:
(8)
式(6)和(7)明显表达出矢量控制中,三相电流与转子位置角θ、交轴电流与定子电流夹角β的关系。当ie一定时,通过改变θ和β的大小,就可以得到不同情况下的有限元静磁场中三相电流的大小,还可以通过式(7)得到电机的交直轴电流的大小。
在Ansoft的静磁场中,若要得到电机的交直轴电感,需要对三相电感矩阵进行换算,具体换算关系为
Ladq=CTLUVWC。
(9)

(10)
式中:CT为C的转置;LUVW为三相电感矩阵。
通过转换得到的交直轴电感的模数为1,要计算电机完整模型电感,还需要考虑电机仿真模数M,每槽导体数Ns,绕组并联支路数a。考虑这些因素后,电机的交直轴电感的换算公式变为

(11)
式中:仿真模数M为8;每槽导体数Ns为40;并联支路数a为1。建模时将转子D轴与定子A相中心线对其,此时θ=0°。
4.2不同电流加载方式对交直轴电感影响
只加载交轴电流iq时,在电机的三相绕组的每个线圈添加激励源,当β=0°时,三相绕组施加的是交轴电流iq,此时id=0A,通过改变三相电流有效值ie的大小,达到改变iq的目的。仿真得到的交直轴电感如图16所示,从图中可以看出,dq轴电感值非常接近,随着iq值的增加,Ld、Lq的值均下降,且Lq的值减小的较快。
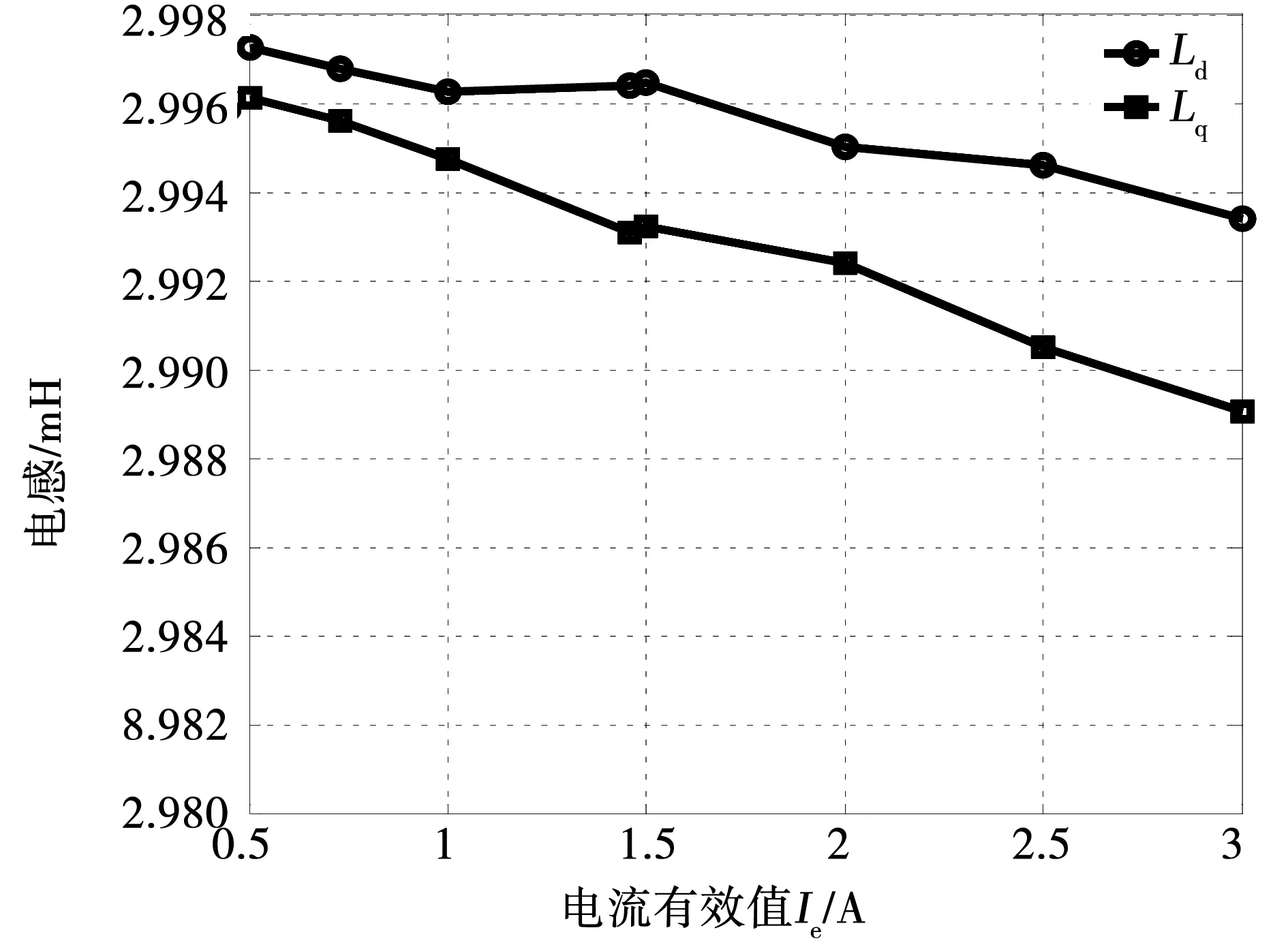
图16 iq对交直轴电感的影响Fig.16 Influence of iqon d-q axial inductance
只加载直轴电流id时,三相绕组电流之间的关系是:iV=iW=-iU/2,此时iq=0。仿真得到的交直轴电感变化情况如图17所示,从图中可以看出随着id的增加,交直轴电感同时减小,且在ie超过1.8A时,由于磁路的饱和影响,直轴电感开始小于交轴电感。
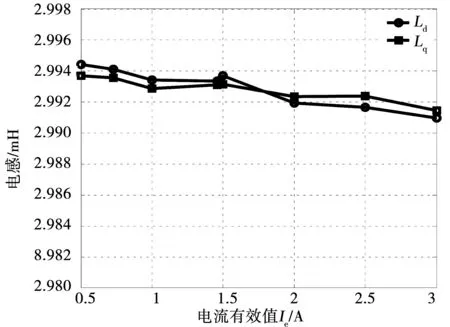
图17 id对交直轴电感的影响Fig.17 Influence of idon d-q axial inductance
以上分析是交轴或直轴电流单独作用的情况,而在电机实际控制中,根据最大转矩/电流比的矢量控制方式,交直轴电流是同时存在的,所以在分析时要考虑到交直轴电感之间的交叉耦合问题,即同时加载直轴电流和交轴电流。
当0°<β<90°时,电机三相绕组中施加电流包含直轴电流id和交轴电流iq两个分量。将ie定为三相绕组的额定电流1.457A,改变β值,仿真得到的交直轴电感如图18所示,从图中可以看出在β=60°时,交直轴电感值趋于一致。

图18 β对交直轴电感的影响Fig.18 Influence of β on d-q axial inductance
永磁同步电机不考虑定子磁链的谐波成分,电磁转矩可表示为
Te=1.5P[φfiq+(Ld-Lq)idiq]。
(12)
其中:Te为电磁转矩;φf为永磁体磁通。
由图16和图17可知,电机在额定电流且id=0和iq=0运行时,直轴电感大于交轴电感,公式(12)中(Ld-Lq)idiq是由电动机的d、q轴磁路不对称而产生的磁阻转矩,当直轴电流id大于0时,所产生的磁场与永磁体产生的磁场方向一致,增加了永磁体磁场。与传统结构相比削弱了直轴电流id对永磁体去磁的影响,即梯形结构盘式电机由于结构的改善,使得产生的磁阻转矩对永磁转矩起到补充作用。
5 结 论
本文针对永磁盘式电机的转子结构进行研究,在Halbach阵列基础上提出了梯形永磁体结构,利用有限元方法计算了气隙磁密、空载反电势畸变率和交直轴电感,可得到结论如下:
1)通过分析不同梯形永磁体结构的气隙磁密,发现永磁体的宽度和厚度影响气隙磁密幅值和谐波含量,其中梯形结构3的基波幅值最大,且谐波含量较小,尤其是三次谐波的含量最小,而在五种结构中该结构的空载反电势畸变率是最小的,因此将其视为最优结构。
2)梯形永磁体结构3与传统等厚5mm结构相比,气隙磁密基波幅值增加了5.37%,与不等厚结构相比增加了4.92%,3次、5次谐波含量减少,空载反电势畸变率满足要求。
3)电机负载情况下,分析了定子绕组电流对交直轴电感的影响,当梯形永磁体结构3的直轴电感大于交轴电感时,可达到充分利用磁阻转矩,提高电磁转矩的作用。
[1]曹永娟,黄允凯,金龙,等.磁极组合型轴向磁场无铁心永磁电机的设计与分析[J].中国电机工程学报, 2014,34(6): 903-909.
CAO Yongjuan,HUANG Yunkai,JIN Long,et al.Design and analysis of a stator coreless axial-flux permanent magnet machine with module poles[J]. Proceedings of the CSEE, 2014,34(6): 903-909.
[2]辜承林.转子无铁心式直流永磁盘式电机的磁场和解析解分析与优化设计[J]. 中国电机工程学报, 1996, 16(2): 125-129.
GU Chenglin. Optimization of permanent-magnet axial-field coreless dc motors based on magnetic-field-network method[J]. Proceedings of the CSEE, 1996, 16(2): 125-129.
[3]PARVIAINEN A, NIEMELA M, PYTHONEN J. Modeling of axial flux permanent-magnet machines[J].IEEE Transactions on Industry Applications,2004, 40(5): 1333-1340.
[4]LIU Cheng Tsung, Chiang T S Zamora. Field-oriented control evaluations of a single-sided permanent magnet axial-flux motor for an electric vehicle[J]. IEEE Transactions on Magnetics, 2003, 39(5): 3280-3282.
[5]褚文强, 辜承林. 新型横向磁通永磁电机磁场研究[J]. 中国电机工程学报, 2007, 27(24): 58-62.
CHU Wenqiang, GU Chenglin. Study on magnet field of novel transverse-flux permanent magnet machine[J]. Proceedings of the CSEE, 2007, 27(24): 58-62.
[6]SADEGHIERAD M,LESANI H,et al.High-speed axial-flux permanent-magnet generator with coreless stator[J]. Canadian Journal of Electrical and Computer Engineering, 2009, 34(2): 63-67.
[7]WANG Rongjie, KAMPER M J, GIERAS J F, et al. Optimal design of a coreless stator axial flux permanent-magnet generator[J]. IEEE Transactions on Magnetics, 2005,41(1): 55-64.
[8]FEI W,LUK P C K,JINUPUN K.Design and analysis of high-speed coreless axial flux permanent magnet generator with circular magnets and coils[J]. Electric Power Applications, 2010,4(9):739-747.
[9]CHOI J Y, S H, et al. Improved analytical model for electromagnetic analysis of axial flux machines with double-sided permanent magnet rotor and coreless stator windings[J]. IEEE Transactions on Magnetics 2011,47(10): 2760-2763.
[10]PARVIAINEN A, PYRHONEN J, MANTERE J. Performance comparison between low-speed axial-flux and radial-flux permanent magnet machines including mechanical constraints[J]. Electric Machines and Drives, 2005: 1695-1702.
[11]GIERAS J F, GIERAS I A. Performance analysis of a coreless permanent magnet brushless motor[C]//37th IAS Annual Meeting of the Industry Applications Conference. Pittsburgh, PA, USA: IEEE, 2002: 2477-2482.
[12]王凤翔. Halbach 阵列及其在永磁电机设计中的应用[J].微特电机, 1999, 27(4): 22-24.
WANG Fengxiang. Halbach array and its application in PM machine design[J]. Small & Special Electrical Machines, 1999, 27(4): 22-24.
[13]范坚坚, 吴建华. 计及齿槽极间隔断 Halbach 型磁钢的PMSM 气隙磁场解析分析[J]. 中国电机工程学报, 2010, 20(12): 98-105.
FAN Jianjian, WU Jianhua. Analytical solution and analysis of airgap magnetic field of PMSM with partition-between-poles Halbach magnet considering effect of slotting[J]. Proceedings of the CSEE, 2010, 20(12): 98-105.
[14]徐衍亮, 姚福安, 房建成. Halbach 磁体结构电动机及其与常规磁体结构电动机的比较研究(I)[J]. 电工技术学报, 2004, 19(2): 79-82.
XU Yanliang, YAO Fuan, FANG Jiancheng.Halbach array permanent magnet machine and performance comparison with the normal array one(I)[J]. Transactions of China Electrotechnical Society, 2004, 19(2): 79-82.
[15]CHAN C C, CHAU K T. An advanced permanent magnet motor drive system for battery-powered electric vehicle[J].Vehicular Technology,1996,45(1):180-188.
[16]王晓远,闫杰,刘艳,等.基于Halbach阵列的永磁同步盘式电机磁钢设计[J]. 微电机, 2005, 38(1): 37-40.
WANG Xiaoyuan,YAN Jie,LIU Yan,et al.The design of disk type coreless PM synchronous motor based on Halbach[J]. Micro-motors. 2005, 38(1): 37-40.
[17]唐任远. 现代永磁电机[M]. 北京: 机械工业出版社, 1997: 326-341.
[18]王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2010: 305-307.
[19]ZHOU Ping, LIN Dingsheng,WIMMER Georg.Determination of d-q Axial parameters of Interior Permanent Magnet Machine [J] . IEEE Transactions on Magnetics, 2010, 46(8): 3125-3128.
[20]王卫平. 内置式永磁同步电机交、直轴电枢反应电抗的准确计算[J]. 微电机, 2009, 42(6): 11-13.
WANG Weiping. Accurate calculation of quadrature-axis and direct-axial armature reaction reactance for an interior permanent magnet synchronous machine[J]. Micro-motor, 2009,42(6): 11-13.
(编辑:刘素菊)
Design and study of disc coreless motor with trapezoidal permanent magnet
XIE Ying,QU Chun-mei
(School of Electrical and Electronic Engineering, Harbin University of Science and Technology,Harbin 150080,China)
A trapezoidal permanent magnetic array is proposed based on the existing Halbach permanent magnetic array, aiming at the axial magnetic field of permanent magnetic disc coreless synchronous motor. The structure and advantages of the motor were shown. The influence of different trapezoidal permanent magnetic arrays on the air gap flux density was studied by finite element method. The optimal rotor structure was proposed according to the harmonic content in the air gap magnetic field and no-load back electromotive force (EMF) distortion rate. The fundamental was heightened and harmonic content was decreased in air gap flux density, with no change of permanent magnetic volume comparing with traditional structure.Considering the characteristic of axial magnetic field, such as ensuring of the parameters of magnetic poles and conductor duty cycle,the design rule of motor was provided.The influence of different stator currents on the d-q axis inductance was calculated under load condition, which offers reference value for the design of this kind of motor.
disc coreless motor; Halbach array; trapezoidal permanent magnet; finite element method(FEM); air gap flux density
2014-09-10
国家自然科学基金(51107022);黑龙江省政府博士后科研启动项目(LBH-Q12061);黑龙江省普通高等学校新世纪优秀人才培养计划(1252-NCET-015);黑龙江省自然科学基金(E201443);哈尔滨市科技创新人才研究专项资金(青年后备人才)(RC2014QN007005)
谢颖(1974—),女,博士,教授,研究方向为电机内电磁场、温度场、振动噪声计算及感应电动机故障的诊断及检测;
曲春梅(1990—),女,硕士,研究方向为永磁盘式电机的研究与分析。
谢颖
10.15938/j.emc.2016.08.010
TM 351
A
1007-449X(2016)08-0074-09
