光伏并网逆变器布谷鸟搜索优化反推控制
2016-08-30阳同光文明才
阳同光, 文明才
(1.湖南城市学院 机械与电气工程学院,湖南 益阳 413000;2.中南大学 信息科学与工程学院,湖南 长沙 410083)
光伏并网逆变器布谷鸟搜索优化反推控制
阳同光1,2,文明才1
(1.湖南城市学院 机械与电气工程学院,湖南 益阳 413000;2.中南大学 信息科学与工程学院,湖南 长沙 410083)
针对并网逆变器模型非线性和电网扰动的问题,提出一种基于布谷鸟搜索算法优化反推控制技术光伏并网逆变器控制策略。首先,建立考虑参数变化和电网扰动的并网逆变器数学模型,设计并网逆变器反推控制。然后,利用布谷鸟搜索算法对不确定性部分进行在线辨识和补偿,消除模型非线性和外部扰动产生的不确定性部分的影响。利用Lyapunov稳定性理论设计控制器自适应律,证明了布谷鸟搜索算法优化反推控制器的稳定性。实验结果表明该方法能实现逆变器精确并网控制,具有较好的动静态性能和较强的鲁棒性。
光伏系统;并网逆变器;布谷鸟搜索算法优化;自适应反推控制
0 引 言
近年来随着全球范围内能源短缺和环境污染的问题日益突出,开发和利用可再生能源日益受到世界各国的关注[1]。光伏发电由于其清洁便利已成为使用最广泛的可再生能源之一。在光伏发电系统中,并网逆变器作为发电系统与电网的接口设备之一,其控制技术一直是研究热点。并网逆变器控制方法主要有矢量控制[1-2]和直接功率控制[3-4]两种,其中,矢量控制通过控制并网逆变器输出电流矢量的幅值和相位,对并网逆变器的有功和无功功率进行控制,以此实现逆变器并网控制。但是矢量控制需要较为复杂的同步速旋转坐标变换和电网电压的相位信息,增加了系统的复杂程度。而直接功率控制对并网逆变器的有功和无功功率进行直接控制,不需进行同步速旋转坐标变换,控制结构简单、动态响应快。但是直接功率控制存在开关频率不固定,导致滤波电路设计困难。
为了克服上述困难,一些新型的控制方法被用于并网逆变器控制。文献[4]提出并网逆变器预测控制,但是有限状态预测控制输出开关频率也不固定,同样存在滤波电感设计的难题。文献[5-7]提出并网逆变器滑模控制方法,虽然滑模控制器具有很强的鲁棒性,但是其抖振现象影响其性能。文献[8-10]提出基于空间矢量调制的无差拍功率控制策略,实现三相光伏并网逆变器有功功率、无功功率的快速跟踪和解耦控制无差拍控制,但是无差拍控制要求脉宽必须当拍计算当拍输出,存在算法复杂,采样频率高等缺点。
上述方法都是建立在并网逆变器精确数学模型的基础上,没有对并网逆变器模型的非线性和外部扰动的影响进行研究。事实上,并网逆变器为非线性系统,难以建立精确数学模型,因此在实际工作过程中,其参数摄动将对其工作性能产生较大的影响。此外,由于不平衡负载引起的电网扰动也是必需考虑的问题。因此,开展考虑并网逆变器非线性和电网扰动等不确定性的控制策略研究具有十分重要的现实意义。
反推控制具有较强的鲁棒性的特点,被广泛用于非线性系统的控制[11-16]。但在设计反推控制过程中,由于被控对象模型通常存在非线性和参数不确定性,将会导致反推控制的控制性能下降[15]。文献[16]为了消除模型非线性和外部扰动的影响,利用高增益观测器辨识模型的非线性和外部扰动,但是观测器增益带来很大的观测噪声。本文在综合考虑并网逆变器模型非线性特性以及电网等外部扰动所形成的不确定性部分,并在此基础上建立并网发电系统的数学模型,将反推控制技术和布谷鸟搜索算法结合,用布谷鸟搜索算法对光伏并网逆变器的不确定性部分进行在线辨识和补偿,从而消除不确定项对控制系统性能的影响,提高系统的鲁棒性。
1 光伏系统数学模型
光伏发电系统的等效电路如图1所示,图中,PV为光伏阵列、C为直流母线电容,L和R为滤波电路,ea、eb、ec分别为三相电网电压。图中,假定三相电感严格对称且等效电感、电阻值分别为L、R,并网逆变器功率开关管为理想状态,其上升、下降时间及死区时间可忽略。

图1 光伏并网逆变器发电系统Fig.1 Diagram for PV grid-connected system circult
在同步旋转dq坐标系下,并网逆变器发电系统数学模型[2]为

(1)
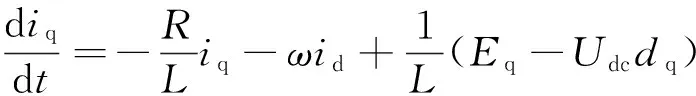
(2)
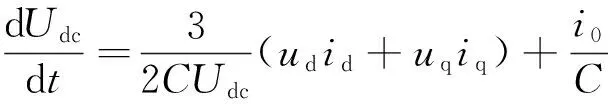
(3)
式中:id、iq、ud、uq分别表示并网逆变器输出电流和并网电压的dq轴分量;Ed、Eq分别表示电网电压dq轴分量;ω表示电网角频率。dd、dq分别为开关函数的dq轴分量。
综合考虑并网逆变器模型参数非线性和电网扰动所产生的不确定性项,令x1=id、x2=iq、x3=Udc则并网发电系统的状态方程为

(4)

(5)
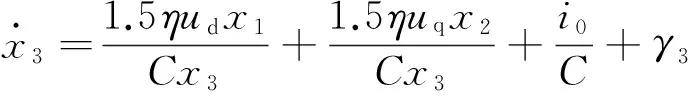
(6)
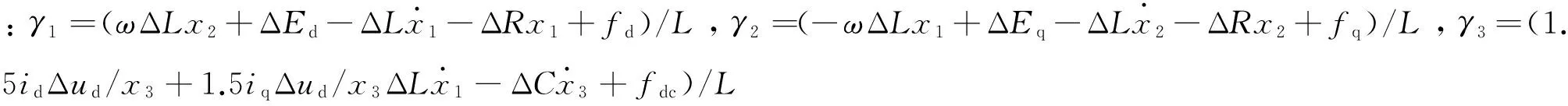
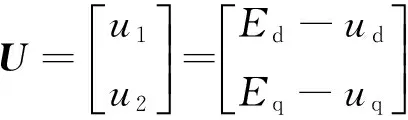

(7)
2 反推控制设计

(8)
对上式求导可得

(9)


(10)
将上式代入式(9)可得

(11)


(12)

(13)
定义Lyapunov函数为

(14)
对上式求导可得
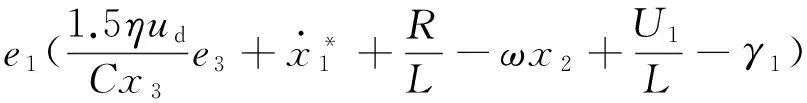
(15)
设计并网逆变器输入控制信号为
ωLx2-k1e1+γ1,
(16)

(17)
将式(16)、式(17)代入式(15)可得

(18)
式(18)表明设计的反推控制系统稳定。
3 布谷鸟搜索自适应反推控制设计
尽管前面设计的反推控制能够在正常情况下确保系统稳定,但是系统参数在工作过程中具有时变性,往往难以测量,此外,系统外部扰动和模型的非线性部分在实际应用过程中也难以预计。为了消除系统不确定部分对控制系统的影响,考虑到布谷鸟搜索算法优化算法较强搜索能力,采用布谷鸟搜索算法对反推控制中非线性部分和外部扰动的不确定性进行辨识和在线补偿。
3.1布谷鸟搜索算法不确定性项估计
布谷鸟搜索(cuckoosearch,CS)算法是由Yang于2009年提出的一种新兴生物启发搜索算法[17]。它通过模拟布谷鸟寄生育雏习性求解最优问题。布谷鸟最特殊的习性是寄生育雏[17]。某些种属的布谷鸟将自己的卵偷偷产入宿主巢穴,由于布谷鸟后代的孵化时间比宿主的幼雏早,孵化的幼雏会本能地破坏同一巢穴中其他的卵(推出巢穴),并发出比宿主幼雏更响亮的叫声。很多宿主通过后代的叫声大小判断其健康程度,而健康后代获得的食物较多,进而拥有更高的存活率。在某些情况下,宿主也会发现巢穴中的陌生卵。这时,宿主将遗弃该巢穴,并选择其他地方重新筑巢。在与宿主不断的生存竞争中,布谷鸟的卵和幼雏叫声均朝着模拟宿主的方向发展,以对抗宿主不断进化的分辨能力[17]。
设在K维搜索空间中,x=(x1,x2...xK)表示每个卵或布谷鸟,并使用两种方法产生后代。第一种使用Lery飞行,有

(19)
其中SL~LK(l),SL~LK(l)为K维Levy分布,rn~NK(0,1),NK(0,1)为K维正态分布;α为步长因子;xb为历史最优解。Levy飞行是一种随机运动,随着迭代次数增加,其方差与迭代次数存在如下关系
σ2(t)~t3-λ,1<λ<3。
(20)
另一种产生新解的方法是使用种群之间的相似性及发现概率pa,其产生公式如下

(21)
其中,ru~U(0,1);ru~UK(0,1),UK(0,1)为定义在[0,1]上的均匀分布,xi,xj和xk为随机选择且互不相同的解;H(·)为Heaviside函数。采用贪婪算法选择新解,Cuckoosearch算法流程如下
Step1:初始化鸟巢数n、Pa、精度和最大迭代次数。
Step2:随机产生n个鸟巢的初始位置xi,i=1,2,3,…,n,每个鸟巢对应神经网络的连接权值。
Step3:对每一个个体计算其适应度值fi(i=1,2,3,…,n)和当前群体最优适应度值以及对应的最佳鸟巢位置。
Step4:判断当前群体最优值满足条件或达到最大迭代次数。
Step5:对所有鸟巢按式(21)更新鸟巢位置,计算适应度值,并对新鸟巢和当前鸟巢进行适应度评价。
Step6:若新的鸟巢适应度好于当前鸟巢,则用新鸟巢位置代替旧的鸟巢位置。否则按照一定的概率Pa丢弃差的鸟巢位置,用式(21)更新鸟巢位置替代丢弃的鸟巢位置,并比较原位置的适应度值,保留适应度值比较优的位置。
Step7:返回步骤4,直到迭代次数达到最大迭代次数N时,停止搜索,输出最佳位置。
布谷鸟搜索优化算法流程图如图2所示。
3.2布谷鸟搜索自适应反推控制设计

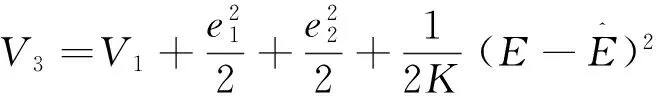
(22)
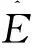

(23)

图2 布谷鸟搜索算法流程图Fig.2 Flow chart of cuckoo search algorithm
由此设计实际的控制输入为

(24)
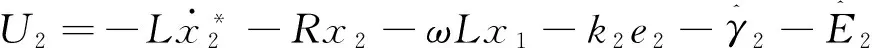
(25)
d轴的实际参考电流值为

(26)
将式(24)、式(25)代入式(23)可得

(27)
式中e=(e1、e2、e3),根据式(27),选择自适应律为

(28)
将其代入式(29),则可得
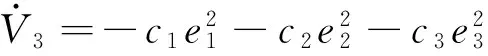
(29)
根据上述分析可知,通过设计式(24)、式(25)和式(28)的控制律和自适应律,可实现并网逆变器直流母线电压、电流id、iq的渐进跟踪,对并网逆变器具有很好的鲁棒性。
对式(31)两边积分可得
V3(0)-V3()≥。
(30)


(31)
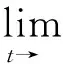
通过上述分析,对于式(7)描述的光伏并网逆变器系统,通过设计式(24)、式(25)的控制律和式(28)表示的自适应律可确保并网逆变器并网电流的渐进跟踪,实现系统的全局一致稳定。布谷鸟搜索算法优化反推控制结构如图2所示。
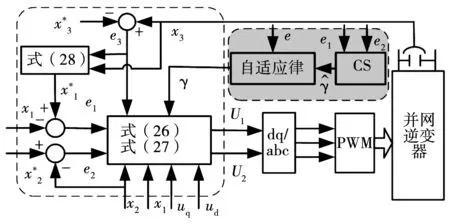
图3 布谷鸟搜索算法优化反推控制光伏系统结构图Fig.3 Structure of CS backstepping photovoltaic system
4 实验结果及分析
为验证布谷鸟搜索算法优化反推控制技术并网逆变器控制的有效性,基于TI公司32定点TMS320F2812DSP搭建实验平台,DSP时钟频率为150MHz,PWM开关频率为10kHz,采样频率为10kHz。实验系统参数如表1所示,实验系统平台如图4所示。布谷鸟搜索算法中选择鸟巢数为50,最大迭代次数为1 000,概率系数Pa=0.25。
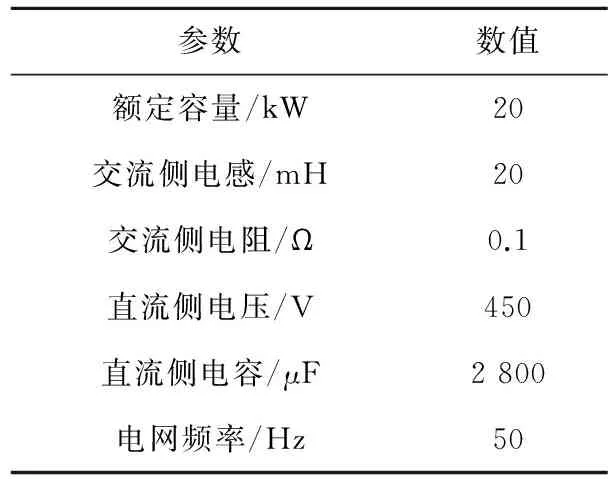
表1 实验参数

图4 光伏并网逆变器实验平台Fig.4 Photoraph of the experimental PV grid-connected inverter
图5为给定有功功率为20 kW、无功功率为0时的实验结果图。从图中可以看出,在布谷鸟搜索算法优化反推控制的作用下,三相并网逆变器输出电流波形正弦度良好,能较好跟随并网电压,实现高功率因数并网。
图6为采用矢量控制(电流内环采用PI控制)时并网逆变器实验结果,从图中可以看出,矢量控制的并网逆变器并网电流波形存在一定的畸变,导致并网电流存在一定的谐波。图7为给定有功功率增加、无功功率为0时候布谷鸟搜索算法优化反推控制并网逆变器实验结果,从中可以看出,当给定有功变化时,并网逆变器输出有功功率能快速跟踪给定有功的变化,输出三相电流幅值有一定增加,仍然保持很好的正弦度。

图5 稳态下布谷鸟搜索算法优化反推控制实验结果Fig.5 Steady experimental results of CSBC

图6 矢量控制(PI控制)实验结果Fig.6 Experimental results of vector control

图7 给定有功功率增加时实验结果Fig.7 Experimental results under active power change
为进一步验证布谷鸟搜索算法优化反推控制技术的优越性,将其与并网逆变器反推控制和矢量控制进行实验对比,对比结果如图8所示。从图8中可以看出,当给定有功功率发生变化时,有功电流分量将发生变化,PI控制的动态响应较慢,并具有一定的超调量,其稳态误差也较大。反推控制虽然消除了超调,但其动态响应速度并不理想,而布谷鸟搜索算法优化反推控制下的电流跟踪性能明显好于反推控制和常规矢量控制。

图8 布谷鸟搜索算法优化反推控制跟踪误差对比实验结果Fig.8 Comparation of track error among PI and CS backstepping control eid
选取总谐波含量、有功电流分量误差和并网功率因数为比较指标,对布谷鸟搜索反推控制、反推控制和矢量控制下并网逆变器性能进行对比,具体对比数据见表2。
表2CBSC、BC 和 PI实验结果对比
Table 2Experiment results of CBSC、BC and PI

指标THD(5%)功率因数电流误差/ACSBC1.780.9930.253BC4.120.9740.512PI4.850.9680.784
从表2可以看出,布谷鸟搜索算法优化反推控制并网逆变器并网电流的总谐波含量THD为2.42%,比反推控制策略的4.12%减小1.7%,而常规矢量控制THD为4.95%,接近国标5%的极限。功率因数接近为1,远高于常规矢量控制,并网电流有功功率分量的误差也较之其他两种控制方法要小。结果表明本文提出的布谷鸟搜索算法优化反推控制方法能在电网扰动的情况下,具有较好的并网电流质量,其抗干扰能力较之反推控制和常规矢量控制得到很大的提升。
5 结 论
针对光伏并网逆变器存在非线性和外部扰动的问题,提出一种基于布谷鸟搜索算法优化反推控制技术光伏发电系统并网逆变器控制方法。该方法具有如下特点:
1)利用布谷鸟搜索算法优化的非线性逼近能力和反推法设计保证控制稳定性的优点,解决了并网逆变器控制器设计中参数非线性和外部扰动产生不确定性的问题,使控制系统具有很强的鲁棒性。
2)本文方法与传统并网逆变器矢量控制相比,并网电流谐波小,具有较强的并网电流质量,并且具有良好的控制性能。
[1]Riad Kadir, Jean Paul Gaubert. An improved maximum power point tracking for photovoltaic grid-connected inverter based on voltage-oriented control[J].IEEE Transactions on industrial electronics, 2011, 58(1):66-75.
[2]张兴,张崇巍,曹仁贤. 光伏并网逆变器非线性控制策略的研究[J].太阳能学报, 2002, 23(6): 770-773.
ZHANG Xin, ZHANG Chongwei, GAO Renxian. Study on nonlinear control of FV parallel feed inverter[J]. ACTA Energiae Solaris Sinica, 2002, 23(6): 770-773.
[3]杨勇, 阮毅. 三相并网逆变器直接功率控制[J]. 电力自动化设备, 2011, 31(9): 54-59.
YANG Yong, RUAN Yi. Direct power control for three-phase grid-connected inverters[J].Electric Power Automation Equipment. 2011, 31(9): 54-59.
[4]陈强, 任浩翰, 杨志超. 三相并网逆变器改进型直接功率预测控制[J].电力自动化设备, 2014, 34(12): 100-105.
CHEN Qiang, REN Haohan, YANG Zhichao. Improved predictive direct power control of three-phase grid-connected inverter[J]. Electric Power Automation Equipment, 2014, 34(12):100-105.
[5]尹璐, 赵争鸣, 贺凡波. 具有高功率因数的三相光伏并网逆变器控制算法[J]. 电力自动化设备, 2012, 32 (10): 1-5.
YIN Lu,ZHAO Zhengming,HE Fanbo. Control algorithm for three-phase grid-connected photovoltaic inverter with high power factor[J]. Electric Power Automation Equipment, 2012, 32 (10):1-5.
[6]侯世英,宋星,孙韬. 采用滑模控制的复用型三相双频并网逆变器[J]. 电机与控制学报, 2013, 17(7):40-45.
HOU Shiying,SONG Xing,SUN Tao. Dual-function three-phase double-frequency grid-connected inverter adopted the sliding mode control [J]. Electric Power Automation Equipment, 2013, 17(7):40-45.
[7]吴忠强,谢建平. 带扰动观测器的网侧逆变器高阶终端滑模控制[J]. 电机与控制学报,2014.18(2):96- 101.
WU Zhongqiang, XIE Jianping. High-order terminal sliding mode control of grid-connected inverter with disturbance observer [J]. Electric Machines and Control,2014.18(2):96-101.
[8]刘孝辉, 郑建勇, 黄金军.光伏并网Z源逆变器无差拍解耦控制策略[J].电力系统自动化,2010, 30 (12): 92-96.
LIU Xiaohui,ZHENG Jianyong,HUANG Jinju.A deadbeat decoupling control strategy of Z-source photovoltaic grid-connected inverter[J]. Automation of Electric Power Systems, 2012, 36(12): 25-30.
[9]吴国祥,杨勇. 三相光伏并网逆变器dq旋转坐标系下无差拍功率控制[J]. 电机与控制学报,2014, 18(12):37-43.
WU Guoxiang,YANG Yong. Dead beat power control in dq rotating reference frame for three-phase photovoltaic grid-connected inverters [J]. Electric Machines and Control, 2014, 18(12): 37-43.
[10]李渊,何凤有,谭国俊.双馈电机系统滑模变结构反演控制的研究[J]. 电机与控制学报,2009,13(1): 15-20.
LI Yuan, HE Fengyou, TAN Guojun. Study on variable structure sliding mode control with backstepping for doubly-fed motor system [J]. Electric Machines and Control, 2009,13(1): 15-20..
[11]方一鸣,李智,吴洋羊. 基于终端滑模负载观测器的永磁同步电机位置系统反步控制[J].电机与控制学报,2014,18(9):105-110.
FANG Yiming,LI Zhi,WU Yangyang. Backstepping control of PMSM position systems based on terminal-sliding-mode load observer[J]. Electric Machines and Control, 2014,18(9):105-110.
[12]方一鸣,焦宗夏,王文宾.轧机液压伺服位置系统的自适应反步滑模控制[J]. 电机与控制学报,2011, 15(10):95-100.
FANG Yiming,JIAO Zongxia,WANG Wenbin. Adaptive backstepping sliding mode control for rolling mill hydraulic servo position system[J]. Electric Machines and Control,2011,15(10):95-100.
[13]董锋斌,钟彦儒.反向递推法在三相四桥臂逆变器控制中的应用[J]. 电机与控制学报,2012,16(4): 30-36.
DONG Fengbin,ZHONG Yanru. Application of backstepping for three-phase four-leg inverter [J]. Electric Machines and Control, 2012,16(4):30-36.
[14]S.Tong, C.Liu, Y.Li. Adaptive fuzzy backstepping output feedback control for strict feedback nonlinear systemswithun known sign of high-frequency gain[J]. Neurocomputing, 2012.77(1):58-70.
[15]王洪斌,张永顺,冯少婵.直驱泵控缸系统建模及自适应反推滑模控制[J]. 电机与控制学报,2011,15(9):92-97.
WANG Hongbin,ZHANG Yongshun,FENG Shaochan. System modeling and adaptive backstepping sliding mode control for direct-drive pump-controlled cylinder [J]. Electric Machines and Control,2011,15(9):92-97.
[16]DaeheeWon, Wonhee Kim, Donghoon Shin. High-gain disturbance observer-based backstepping control with output tracking error constraint for electro-hydraulic systems[J]. IEEE Transactions on Control Systems Technology, 2015,23(2):787-795.
[17]张永韡, 汪镭, 吴启迪. 动态适应布谷鸟搜索算法[J].控制与决策,2014,29 (4):617-622.
ZHANG Yongwei, WANG Lei, WU Qidi. Dynamic adaptation cuckoo search algorithm[J]. Control and Decision,2014,29 (4):617-622.
(编辑:刘素菊)
Cuckoo search optimization backstepping control of photovoltaic system grid-connected inverter
YANG Tong-guang1,2,WEN Ming-cai1
(1.College of Mechanical and Electrical Engineering,Hunan City University, Yiyang 413000, China;2.College of Information Science and Engineering,Central South University, Changsha 410083, China)
A method based cuckoo search optimization backstepping control is proposed to solve the problems of inverter model’s nonlinear and disturbances in this paper. At first, taking parameter variations and external disturbances into account, a dynamic mathematical model was derived , and a backstepping control was set up based on this model. Then, to identify and compensate the time-varying and nonlinear uncertain impacts on control system, cuckoo search was used to approximate the uncertain and unlinear part of inverter model online. The stability and the adaptive law of cuckoo search backstepping control were ensured by applying Lyapunov stability theory. The experimental results show that this method can control the grid-connected inverter accurately and has the advantages of better static and dynamic performance and robustness.
photovoltaic system; grid-connected inverter; Cuckoo search; adaptive backstepping control.
2015-05-19
国家自然科学基金(61273158);湖南教育厅科学研究项目(13A015)
阳同光(1974—),男,博士,副教授,研究方向为智能控制、新能源技术;
文明才(1963—),男,教授,研究方向为机器人控制、新能源技术。
文明才
10.15938/j.emc.2016.08.014
TK 513.5
A
1007-449X(2016)08-0105-07
