基于虚拟阻尼补偿的恒功率负载系统控制方法

宋欣达，　郑世强

(1.北京航空航天大学 惯性技术重点实验室，北京 100191；2.北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；3.北京市高速磁悬浮电机技术及应用工程技术研究中心，北京 100191)



基于虚拟阻尼补偿的恒功率负载系统控制方法

宋欣达1，2，3，郑世强1，2，3

(1.北京航空航天大学 惯性技术重点实验室，北京 100191；2.北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；3.北京市高速磁悬浮电机技术及应用工程技术研究中心，北京 100191)

电动机负载广泛存在于各个工业领域，其闭环控制对前级功率系统表现为恒功率负载(constant power loads, CPL)特性，即负阻抗特性，给系统带来了稳定性的影响。针对基于前置BUCK变换器的电动机驱动系统稳定性问题进行了研究。首先对基于前置BUCK变换器的电机驱动系统进行了建模，分析了影响系统稳定性的机理，在此基础上提出了一种基于虚拟阻尼补偿的控制策略，这种方法可以在不增加系统损耗的前提下有效抑制负阻抗特性对直流母线电压的影响，并给出了补偿系数的设计流程。仿真和实验证明这种方法提高了系统稳定性，增加了电机驱动系统稳定带载的能力。

电机驱动；buck；恒功率负载；虚拟阻尼补偿；稳定性

0　引　言

恒功率负载通常是指正常工作时系统从前级电源吸收的功率基本保持恒定值的一类负载[1]，即输出功率基本恒定的负载，广泛存在于各类工业设备中，例如电机驱动系统、理想闭环的功率转换模块、以及各类分布式配电系统等都具有恒功率负载特性[2-4]，其具有的负增益阻抗特性影响了系统的稳定性。

近年来，国内外学者针对恒功率负载的特性及其在各个领域的应用进行了广泛研究[2-10]，抵消恒功率负载的负增益阻抗特性的方法总的来说可以分为无源法和有源法两类，无源法通过增加阻尼补偿电路[5-7]或者阻尼滤波器[8]以增强系统的稳定性，优点是算法简单可靠性较高，然而体积质量大且增加额外硬件和损耗的缺点也显而易见；有源法则通过建立小信号模型，在控制回路中增加稳定模块[9]、阻抗补偿器[10]、功率补偿模块[11-12]等方式抵消负阻抗特性，增加系统的稳定性，此类方法不增加额外的硬件和损耗，尤其适合功率级联系统，但对系统的控制性能要求较高。

永磁电机由于具有能量密度大、效率高、体积小等优点，广泛应用于风机和泵类等各工业领域[13-16]，其逆变驱动系统具有典型的恒功率负载特性。前置DCDC变换器电机驱动系统具有谐波含量低、整体效率高等优点[17-19]，本文以前置BUCK变换器的永磁电机驱动系统为研究对象，在前人研究的基础上，给出系统稳定的条件。并从恒功率负载特性入手，提出一种抑制恒功率负载特性的虚拟阻尼补偿法，在不增加系统损耗的前提下，提高系统的稳定性和带恒功率负载能力。

1　基于前置BUCK变换器的电机驱动系统建模

基于BUCK变换器的电机驱动系统主要包含整流模块、BUCK斩波模块和逆变模块等，其原理图如图1所示。正常驱动电机时刹车管不工作，因此忽略其影响，逆变桥驱动电机为理想闭环，则对于前级功率变换模块则等效为CPL，则CPL的电压v、电流i和功率P的关系为

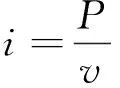
(1)

对于一个给定的工作点P(I,V)，可以得到工作点附近电流变化率

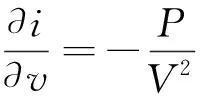
(2)

图1　基于前置BUCK变换器的电机驱动系统模型Fig.1　Model of the motor drive system based pre-BUCK converter

则在此工作点处的切线方程为

(3)

其中，令：

(4)

则有

(5)

由式(5)可知恒功率负载可以等效为一个负电阻RCPL和一个恒流源ICPL的并联电路，其中恒流源ICPL为常数值，不会对系统的稳定造成影响，负电阻RCPL会使系统产生两个右半平面极点从而造成系统不稳定，这就是恒功率负载的复阻抗特性。另外，假设电网电压稳定，忽略输入电压波动以及整流桥的损耗和压降的影响，则可以近似认为BUCK斩波电路的前级电压Vin为常数，即为一个恒压源。由此可知图1(a)可以简化为图1(b)所示的系统模型。由于断续电流模式(DCM-discontinuous current mode)带CPL负载是稳定的[20]，因此着重研究连续电流模式(CCM-continuous current mode)下系统的稳定性。忽略控制量占空比d的波动，则在CCM模式下可以进一步简化为如图1(c)所示的模型。其中dVin为直流侧前级可控电源，L为滤波电感，C为滤波电容，RL和RC分别为L和C的串联等效电阻(ESR-equivalent series resistance)，RCPL为CPL的等效负电阻，ICPL为CPL的等效电流源，iL为电感电流，iC为电容电流，vC为电容电压，则图1(c)所示的电路方程可写为：

(6)

由式(6)得到系统的传递函数为

(7)

式中：a0=LCRCPL+LCRC;a1=CRCRCPL+CRCRL+CRCPLRL+L;a2=RL+RCPL。

由式(7)可得到系统的极点

(8)

由式(8)可知，若当式(8)中分子根号内的部分大于零时，系统有两个实根，且在实际应用中通常有

|RCPL|>RC。

(9)

因此式(8)的分母符号为负，若使系统稳定需

CRCRCPL+L+CRCRL+CRLRCPL<0。

(10)

则系统有两个位于复平面左半平面的极点，若当式(8)中分子根号内的部分小于零时，系统有一对共轭复根，使系统稳定同样需要满足式(10)，才能得到两个复平面左半平面的共轭复根，因此，系统稳定的条件即为式(10)。由式(10)可得

(11)

则系统稳定的条件为式(9)和式(11)，结合式(4)，令Vo为vo的均值，则有

(12)

式(12)为系统稳定工作的条件，由式(12)得到的功率P为当前参数下稳定驱动的恒功率负载的最大功率。将表1中的数据代入式(12)，得到稳定的最大功率值为61.18 kW，由于实际电路中杂散电感的影响，实际的最大稳定输出功率值比式(12)计算得到的理论值低。

结合式(6)可得系统结构框图如图2所示，图中vref为控制电压参考值，vo为控制电压实际值，Vtr=5 V为三角载波的幅值，GPI为反馈控制器，其表达式为KP+Ki/s，其中KP和Ki分别为比例系数和积分系数。

基于表1所示的参数，对图2所示的系统做出输出负载功率P从10 kW到100 kW时的Bode图和极点分布图如图3所示。

图2　带CPL负载的BUCK变换器的系统结构框图Fig.2　Control scheme of BUCK converter with CPLs

图3(a)为系统Bode图，由图可知，随着功率的升高，系统的幅频特性在转折频率处的频率响应峰值逐渐增大，系统稳定性逐渐变差，直到功率为61.18 kW时达到临界稳定，继续升高则系统失稳。图3(b)为系统极点分布图，由图中可知，随着功率的升高，系统的极点逐渐靠近虚轴，当功率为61.18 kW时，极点位于虚轴上，系统处于临界稳定状态，继续升高功率，则极点位于复平面右半平面，系统失稳。

表1　实验电路参数与控制参数

图3　负载功率P由小增大时系统的Bode图和极点分布图Fig.3　Bode plot and the poles distribution of the system when the power of the load increasing

2　消除复阻抗特性提高稳定性方法

一些研究表明，采用阻尼补偿网络，即在转折频率处增加阻尼的方法可以提高系统稳定性，从而提高系统的稳定输出功率[5-7]。然而这些方法都是通过增加硬件网络从而重新配置系统极点以满足稳定性要求，因此会增加额外的硬件损耗，使系统效率降低，并且整体系统的体积重量均有所增加，不适合较大功率负载的驱动系统。

由式(12)可知调整RC、RL效果相似，以RL为例，由式(11)得

(13)

(14)

令RLact为实际的电感ESR值，则由式(13)、式(14)可知，使系统稳定而需要增加的电感ESR值ΔRL需满足

ΔRL>RLmin-RLact。

(15)

如果将等值电阻与电感串联则可以使系统在此工作点处稳定，然而这样会增加系统的损耗，所增加的损耗为

(16)

当电机工作在满载额定转速时，结合表1参数可得增加的损耗ΔP为1 387.7 W，大大降低了系统整体效率。采用RC为调整参数的分析过程与之相似，可以得到类似结果。

因此，采用一种不增加硬件的虚拟阻尼的方法提高系统稳定性。基于以上分析可知，适当提高RL和RC都可以增加系统的带载能力，但是由图2可知，RC直接对输出电压产生影响，不便于在控制端反馈调节，因此选用RL为调整参数。先将iL值测量引出，然后引入一个虚拟补偿系数Rcpt，二者求积之后将其反馈至控制器，与反馈控制器的输出做差之后产生占空比d的控制量。可知虚拟增加的滤波电感ESR值ΔRL由式(17)得到，令k为补偿系数增益,则虚拟补偿系数计算公式为式(18)。

(17)

(18)

由上面分析可知，虚拟阻尼补偿法第一步由式(4)确定当前工作点处系统的恒功率负载阻值RCPL；第二步由式(14)得到系统在当前工作点稳定的滤波电感ESR值边界值RLmin；第三步由式(15)确定需要增加的最小的电感ESR的差值ΔRL；如果第三步中得到的ΔRL<0，则说明系统稳定，不启用阻尼补偿，相反则说明系统不稳定，启动阻尼补偿，由式(18)得到虚拟补偿系数Rcpt。

在第三步中所确定的电感ESR的差值ΔRL是使系统稳定工作的最小值，为使系统具有足够大的相对稳定性，需要在此基础上选取较大的ΔRL值，参数整定方法如下。

三是水工程建设和管理仍相对滞后。尽管我国已初步形成了蓄引提调相结合的水资源配置格局和基于大江大河干流的防洪减灾体系，但洪灾水患问题和工程性缺水仍普遍存在，水利投入仍存在较大缺口。农田水利、中小河流治理、农村饮水安全工程、小型水库病险率高等问题突出，亟待加强专项治理。

首先由式(14)计算得到边界值RLmin，令补偿系数增益k=1，带入式(18)得到当前工作点的边界补偿系数Rcpt，然后由式(19)求得当前参数下系统的谐振峰值Mr，其中ξ为补偿之后整个系统传递函数的阻尼系数，结合式(18)和后面给出的式(24)，可推导出其表达式为式(20)，若未达到期望值Mrref，则加大补偿系数增益k，直至获得期望值，从而确定最终的补偿系数。

(19)

(20)

为获得较好的相对稳定性，工程经验中通常选取Mr<1.4[21]，因此选取谐振峰值期望值Mrref=1.4。选取滤波电容C为600 μF，其它参数和表1中一致，当分别令补偿系数增益k=1和6.5时，系统Bode图如图4所示，从图中可知，选取较小容值滤波电容时系统不稳定，当开启虚拟阻尼补偿时系统稳定，且随着补偿系数增益k的增大，谐振峰值减小，系统相对稳定性明显提高，由此可知该参数整定方法有效，且在同等条件下可以选取较小的滤波电容。

值得注意的一点是，由于虚拟增大了滤波电感的ESR值，此时输出电压的稳定值会产生一个额外的压降vdrop

vdrop=(RLmin-RLact)iL。

(21)

按照表1中的参数计算当前工作点处系统稳定，虚拟补偿法未起作用，输出压降为0 V。当滤波电容C选为600 μF，其它参数和表1中一致，则压降为11 V左右，则在当前工作点处转速相差约680 r/min。此输出压降是由于iL反馈值的直流分量引入了控制器所造成的，实际上，在LC的谐振频率f处产生的振荡是引起系统输出不稳定的根本原因，谐振频率由式(22)得到，因此只要在谐振频率f附近将iL反馈值引入控制器就可以避免由其直流分量引起的输出电压降低的现象，因此在iL反馈环节加入带通滤波器Gb(s)，其计算公式由式(23)得到。

图4　应用虚拟阻尼补偿法后的系统Bode图Fig.4　Bode plot of the system after employing virtual damping compensate method

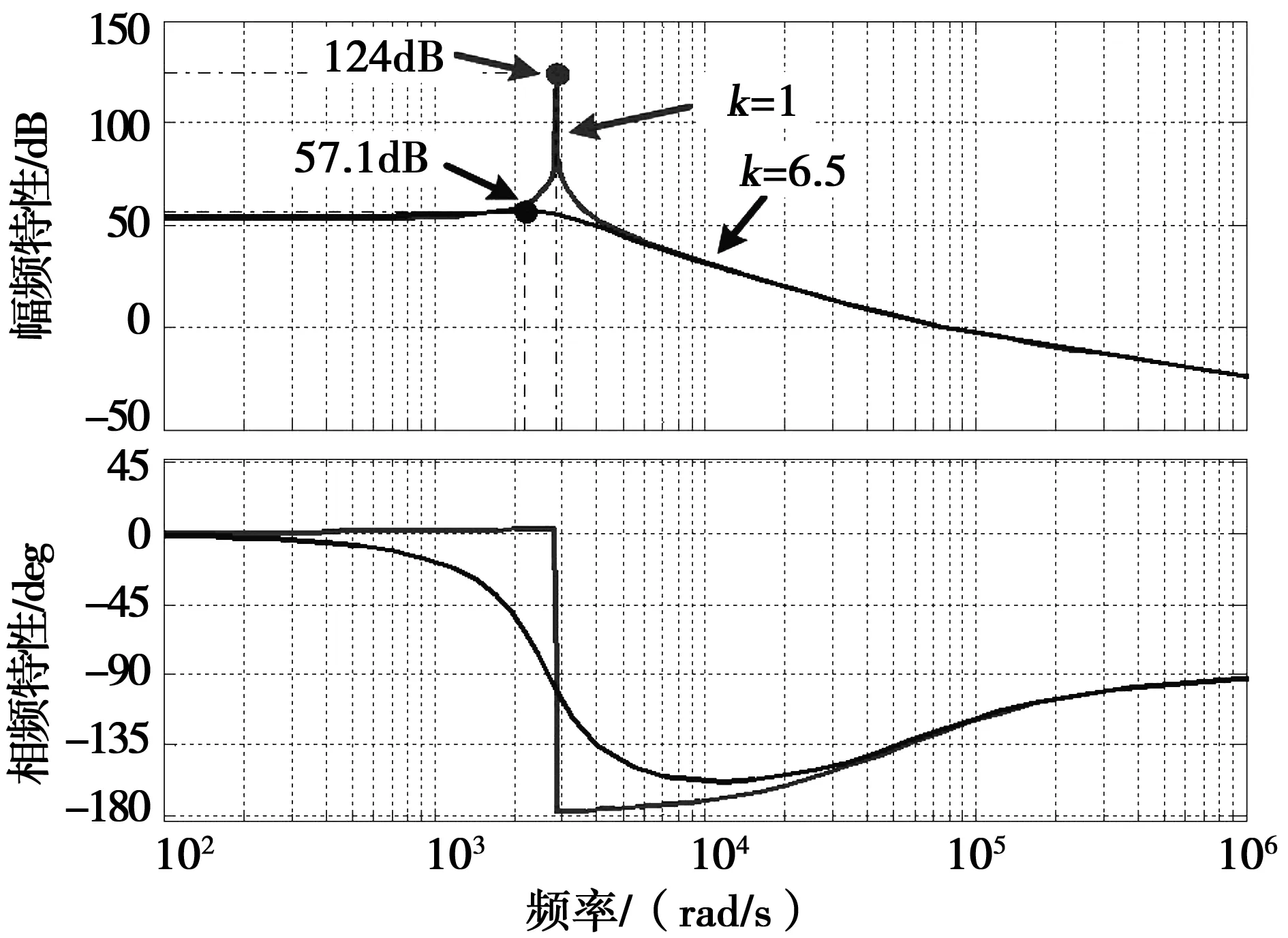
图5　带通滤波器Gb(s)在不同阻尼比ξc下的Bode图Fig.5　Bode plot of the BP filter Gb(s) with different damping ratio ξc

(22)

(23)

式(23)中ξc和ωc分别为带通滤波器的阻尼比和中心频率。选取滤波电容C为600 μF，则谐振频率f为459 Hz，令ωc=459 Hz，则Gb(s)在不同的阻尼比ξc下的幅频特性如图5所示，可知Gb(s)在频率ωc处无衰减，在低频段和高频段有良好的幅值衰减，说明此BP滤波器可以无衰减的通过谐振频率，同时可以很好的阻隔直流分量和高频噪声通过。为了保证在谐振频率附近有足够的带宽，同时在低频段和高频段有足够的衰减幅值，选取阻尼比ξc=0.7。

由上述分析可知，应用虚拟阻尼补偿法之后的系统结构框图如图6所示，由图中可知，改进后系统的传递函数为

(24)

式中，特征方程Δ为

Δ=(RCPL+RC)LCs2+[CRCRCPL+

CRCRL+CRCPLRL+L+

(25)

结合式(25)和式(8)可得改进后系统的极点，可知当选取合适的Rcpt值时，可以将系统的极点配置到复平面左半平面，从而抵消动态复阻抗特性，使系统稳定并具有一定的相对稳定裕量。

图6　采用虚拟阻尼补偿法后带CPL负载的BUCK变换器系统结构框图Fig.6　Control scheme of BUCK converter with CPLs after employing virtual damping compensate method

图7　仿真和实验平台系统结构图Fig.7　System scheme of simulation and experiment

3　仿真与实验

3.1仿真验证

为了验证上述理论分析的正确性，在Matlab环境下搭建了如图1所示的仿真平台，其整体系统结构图如图7所示，其中电容C为600 μF，其余参数按照表1设置，结合上节所述方法，分别在输出功率为60 kW和100 kW时选择不同的虚拟补偿系数增益k，系统频率相应曲线如图8所示，由图中可知，当k=0即未开启虚拟阻尼补偿时，系统处于不稳定状态；当k=1即虚拟阻尼补偿系数为最小值时，系统稳定但谐振峰值Mr很大，系统的相对稳定裕量较小；当k值为整定之后的值时，系统稳定并具有较小的谐振峰值。

图9　未使用虚拟补偿法仿真结果Fig.9　Simulation results before virtual damping compensating

仿真时先将母线电压升至400 V，然后增加负载功率，在0.2 s时负载由0切换至60 kW，在0.4 s时切换至100 kW，按照输出功率60 kW计算，则临界Rcpt的值为0.000 95。如在加载的过程中Rcpt值固定不变，则仿真结果如图9所示，由图中可知第一次切换后母线电压有收敛趋势，可知此时系统还处于稳定状态，第二次切换后母线电压和输出功率都开始发散，系统逐渐崩溃；同等条件下应用第二节中所述的方法整定虚拟补偿系数增益k值从而得到不同的虚拟阻尼补偿系数Rcpt，仿真结果如图10所示，由图中可知系统在100 kW以内母线电压都很稳定，纹波值在3.8%以内。

3.2实验验证

按照图1所示的系统结构图搭建实验平台如图11所示，由图可知实验平台由控制系统、基于前置BUCK调压的电机驱动系统和基于两台永磁电机的对拖系统组成，其中控制系统主要基于DSP(TMS320F28335)和FPGA(XC2S200E)构成的，对拖实验平台由两台永磁电机构成，一台作为电动机(主动机)，另一台作为发电机(被动机)，两台电机由柔性联轴器联接，发电机外接电阻箱，通过切换电阻箱的功率档而选择负载功率，实验平台参数与仿真参数一致。实验所用永磁电机参数如表2所示。

图10　使用虚拟补偿法仿真结果Fig.10　Simulation results after virtual damping compensating

变量数值极数4额定功率/kW100额定电流/A218额定转速/(r/min)32000转动惯量/(kg·m2)0.024

实验中逐步提高母线电压，电机转速随之升高，为确保安全运行，在升速过程中逐步加载，当母线电压升至400 V时，电机转速升至20 000 r/min，此时负载加至50 kW，此时使母线电压保持不变，小幅加载，当加至60 kW时母线电压纹波增大，如继续加载系统即趋于失稳，实验波形如图12(a)所示。当在50 kW切换至虚拟阻尼补偿法时，继续加载至60 kW，母线电压纹波减小，实验波形如图12(b)所示。由实验结果可知，采用虚拟补偿法后系统的稳定域增大，带载能力增强。由于负载箱已经切换至满档，如要继续加大功率只能提高电机转速，但是实验所用的磁悬浮电机在20 000 r/min时已进入挠性模态区，如果继续升速则有可能转子撞边失稳，导致系统故障，因此未继续升速加载实验。

图9　补偿前后60 kW直流母线电压实验波形Fig.9　Experimental results of the bus voltage with the load of 60kW before and after compensating

图10　补偿前后60 kW输出功率实验波形Fig.10　Experimental results of the power before and after compensating

4　结　论

闭环控制的电机驱动系统具有恒功率负载的负阻抗特性，本文针对基于前置BUCK调压的永磁电机驱动系统，首先建立了系统模型，其次分析了影响系统稳定性的因素和稳定条件，在此基础上提出了一种基于虚拟阻尼补偿法的控制策略，并给出了补偿系数的设计流程，最后搭建了实验平台并验证所提出方法的有效性。仿真和实验结果都表明，对于一个给定的前置BUCK的恒功率负载系统，合理选择虚拟补偿系数，可以在不增加系统损耗的情况下增大系统的稳定范围，同时在较小容值滤波电容的前提下获得很好的相对稳定性，大大提高了系统带恒功率负载的能力。

[1]RIVETTA C, WILLIAMSON G A,EMADI A. Constant power loads and negative impedance instability in sea and undersea vehicles: statement of the problem and comprehensive large-signal solution[C]//IEEE Electric Ship Technologies Symposium, 2005: 313-320.

[2]PIERRE M,BABAK N,SERGE P.General active global stabilization of multiloads DC-power networks[J].IEEE Transactions onPower Electronics, 2012, 27(4):1788-1798.

[3]MOHAMED Y A,RADWAN A A,LEE T K. Decoupled reference-voltage-based active DC-link stabilization for PMSM drives with tight-speed regulation[J].IEEE Transactions on Industrial Electronics, 2012, 59(12):4523-4536.

[4]王建华, 张方华, 龚春英, 等. 带恒功率负载的DC/DC变换器起动过程分析[J]. 电工技术学报, 2009, 24(4): 121-125.

WANG Jianhua, ZHANG Fanghua,GONG Chunying, et al.Start-up process analysis of DC/DC converter withconstant power Load[J]. Transactions of China Electrotechnical Society, 2009, 24(4): 121-125.

[5]LIU Xinbo, ZHOU Yuanjun,ZHANG Wei, et al. Stability criteria for constant power loads with multistage LC filters[J]. IEEE Transactions on Vehicular Technology, 2011, 60(5):2042-2049.

[6]刘欣博, 周元钧, 张巍.具有阻尼滤波器的恒功率负载系统在大扰动下的稳定性[J].电工技术学报, 2011, 26(1):154-160.

LIU Xinbo, ZHOU Yuanjun, ZHANG Wei. Large signal stability criteria for constant power loads with damped filters[J].Transactions of China Electrotechnical Society, 2011, 26(1):154-160.

[7]MAURCIO C,LEI Xing,JIAN Sun.Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.

[8]ERICKSON R W. Optimal single resistors damping of input filters[C]//Proceedings of the Applied Power Electronics Conference and Exposition, 1999: 1073-1079.

[9]LIUTANAKUL P,AWAN A B,PIERFEDERICI S,et al. Linear stabilization of a DC-bus supplying a constant power load: a general design approach[J].IEEE Transactions on Power Electronics, 2010, 25(2):475-488.

[10]AMIR M R,ALI E. Active damping in DCDC power electronic converters: A novel method to overcome the problems of constant power loads[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5):1428-1439.

[11]PIERRE M,DIDIER M,BABAK N,et al.Large-signal stabilization of a DC link supplying a constant power load using a virtual capacitor impact on the domain of attraction[J].IEEE Transactions on Industrial Applications, 2012, 48(3):878-887.

[12]张旭辉, 温旭辉, 赵峰. 抵消恒功率负载负阻抗特性影响的双向Buck/Boost变换器控制策略[J].电工技术学报, 2013, 28(11):195-228.

ZHANG Xuhui, WEN Xuhui, ZHAO Feng. The control scheme counteracting negative impedance of constant power load for bi-directional buckboost[J]. Transactions of China Electrotechnical Society, 2013, 28(11):195-228.

[13]THIERRY B, NICOLAS L,BABAK N,et al. Synchronous demodulation of control voltages for stator interturn fault detection in PMSM[J]. IEEE Transactions on Power Electronics, 2013, 28(12):5647-5654.

[15]LIN F, HUNG Y,HWANG J, et al. Fault-tolerant control of a six-phase motor drive system using a takagi-sugeno-kang type fuzzy neural network with asymmetric membership function[J].IEEE Transactions on Power Electronics, 2013, 28(7):3557-3572.

[16]纪历，徐龙祥.高速永磁同步电机无传感器控制[J].电机与控制学报, 2011, 11(9):24-30.

JI Li, XU Longxiang.Sensorless control of high speed permanent magnet synchronous motor[J]. Electronic Machines and Control, 2011, 11(9):24-30.

[17]FANG Jiancheng, LI Wenzhuo, LI Haitao. Self-compensation of the commutation angle based on DC-link current for high-speed brushless DC motors with low inductance[J]. IEEE Transactions on Power Electronics, 2014, 29(1):428-439.

[18]FANG Jiancheng, ZHOU Xinxiu, LIU Gang. Precise accelerated torque control for small inductance brushless DC motor[J]. IEEE Transactions on Power Electronics, 2013, 28(3):1400-1412.

[19]许建平，牟清波，王金平，等.脉冲序列控制DCM Buck变换器输出电压纹波研究[J].电机与控制学报, 2010, 14(5):1-6.

XU Jianping, MOU Qingbo, WANG Jinping, et al.Output voltage ripple of pulse train controlled DCM buck converter[J]. Electronic Machines and Control, 2010, 14(5):1-6.

[20]SUN J, MITCHELL D M, GREUEL M F.Modeling of PWM converters in discontinuous conduction mode—A reexamination[C]//Proc. 29th IEEE Power Electron. Spec. Conf., 1998:615-622.

[21]胡寿松. 自动控制原理[M].北京：科学出版社,2002.

(编辑：贾志超)

Constant power loads system control scheme based on the virtual damping compensation

SONG Xin-da1，2，3,ZHENG Shi-qiang1，2，3

(1.Science and Technology on Inertial Laboratory, Beijing University of Aeronautics and Astronautics, Beijing 100191,China;2.Novel Inertial Instrument & Navigation System Technology Key Laboratory of Fundamental Science for National Defense,Beijing University of Aeronautics and Astronautics, Beijing 100191, China; 3. Beijing Engineering Research Center of High-Speed Magnetically Suspended Motor Technology and Application, Beijing 100191,China)

The motor loads, existing in many industrial fields, behave as constant power loads (CPLs) with negative incremental impendence which may destabilize the system when tightly regulated. In this paper, the stability of BUCK converter with constant power load (CPL) is studied. The model of the motor driving system based pre-BUCK converter was established. The mechanism of the stability impact of the system was analyzed. A new control scheme of neutralizing the negative impedance degenerating the bus voltage based virtual damping compensation was proposed, and the process of compensating coefficient design was given. The simulation and experimental results demonstrate that the proposed method improves the stability of the system with constant power loads.

motor drive; BUCK; constant power load; virtual damping compensation; stability

2015-09-06

国家自然科学基金(61573032)

宋欣达(1981—)，男，博士研究生，研究方向为电机驱动、磁悬浮电机控制；

郑世强(1981—)，男，博士，讲师，研究方向为磁悬浮电机、磁悬浮控制。

宋欣达

10.15938/j.emc.2016.08.001

TM 355

A

1007-449X(2016)08-0001-09