MMC控制策略比较分析研究

李威，　李庚银

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)



MMC控制策略比较分析研究

李威，李庚银

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)

为了研究MMC的控制算法，将模型预测控制应用于MMC系统中，为了获得更好的控制效果，在模型预测控制中引入了死区补偿；并与传统的PI控制器进行深入比较分析。最后通过样机实验表明：两种控制算法在控制MMC输出电压、电流，环流和电容电压平衡控制等方面均具有很好的控制效果；尽管模型预测控制输出电流波形质量不如传统PI控制器优良，但是在电容电压平衡方面表现出很大的优势；并且由于模型预测控制能知晓下一时刻的开关状态，并能预测最优的开关组合状态，所以比传统PI控制表现出更快的动态响应特性。

模块化多电平变换器；模型预测控制；传统PI控制；死区控制；环流抑制；电容电压均衡控制

0　引　言

模块化多电平变换器(modular multilevel converter, MMC)是由德国西门子公司于2002年首先提出来的一种多电平变换器拓扑结构[1]，与其他多电平变换器相比，MMC具有无可比拟的优势：模块化设计易于扩展到更高电压等级，输出波形畸变率低，电容电压平衡易于控制，子模块故障时可以实现容错控制以及MMC提供一个公共直流母线，易实现背靠背连接等[2-3]。虽然MMC拓扑与其他多电平变换器相比具有很多优势，但是MMC在高电平输出时，控制器不仅要实现多电平输出，还要控制子模块电容电压均衡和抑制三相之间由于能量不均衡引起的相间环流，这些都是MMC亟需解决的问题。因此研究简单有效的策略平衡电容电压和抑制相间环流成为了国内外学术界研究的热点。

到目前为止，世界各国的专家学者已提出来很多基于PI控制器的MMC内、外特性控制算法[4-9]。其中文献[4-5]推导了d-q旋转坐标系下MMC开关周期平均模型，并在此基础上设计了d-q电流解耦控制系统；文献[6]根据d-q旋转坐标系下的MMC小信号模型，得到MMC开环传递函数和动态时间常数；为了抑制内部环流，文献[7-8]首先将三相环流经abc/dq坐标变换，然后d轴和q轴分别通过两个PI控制器来抑制内部环流；文献[9]对电容电压控制采用了电压平衡控制和电压平均控制。

模型预测控制具有快速的动态响应能力，灵活性以及易于数字实现等特点，通过选择合理的价值函数，使用单一的控制器就能实现对MMC输出电流、子模块电容电压和相间环流的有效控制。文献[10]针对传统的预测模型控制计算量庞大的缺点，深入分析MMC工作原理，提出了一种提高计算速度的优化方法。文献[11]针对MMC-STATCOM补偿不平衡负载的情况，提出了采用双同步坐标变换解耦的方法模型预测控制算法。文献[12]将模型预测控制成功应用到MMC-HVDC系统中，具有良好的动态响应特性。

尽管已有很多文献采用传统PI控制算法和模型预测控制算法对MMC进行了系统的研究，但是鲜有文献对传统PI控制与模型预测控制算法的优缺点进行比较分析。考虑到文献[9]中的PI控制算法既可以应用于单相MMC系统，又可以应用于三相MMC系统，所以本文采用该控制算法与模型预测控制算法相比较分析。并在模型预测控制中加入了死区控制，最后通过搭建实验平台，比较分析两种控制算法的优缺点。

1　MMC拓扑结构及数学模型

如图1所示为MMC的拓扑结构图，MMC由三相6桥臂组成，每相上、下桥臂各包含N个子模块(sub-module, SM)和一个电抗器Ls串联构成，三相之间以及6个桥臂之间完全对称，全部电气参数的取值均相同。其中，桥臂电抗器Ls起到降低桥臂电流谐波畸变率和抑制相间环流的作用，同时在MMC发生严重的交、直流故障情况下抑制故障电流的上升速率，以保护MMC设备的安全运行。如图1左上角所示为子模块的拓扑结构，子模块主要由一个半桥与直流电容并联组成。每个子模块可以看成是一个二端口元件，通过控制功率管的导通和关断，子模块可以输出+Uc或者0。如表1所示为子模块的四种工作模式，其中“1”表示IGBT导通，“0”表示IGBT关断。与传统的两电平拓扑结构不同，MMC在直流侧正负极之间可不接直流储能电容，依靠任意时刻每相上、下桥臂投入恒定数目的子模块实现电压支撑；在正常情况下，MMC直流侧正、负极电压分别为+Udc/2、-Udc/2。

图1　MMC及其子模块拓扑结构Fig.1　Topology structure of MMC and its sub-model

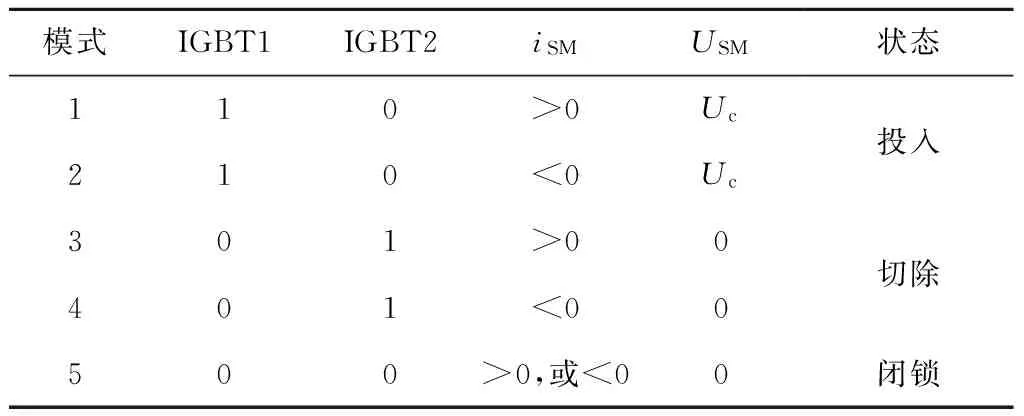
模式IGBT1IGBT2iSMUSM状态110>0Uc210<0Uc投入301>00401<00切除500>0,或<00闭锁

由基尔霍夫电压定律可以得到x相上、下桥臂电压为

(1)

定义第x相环流为

(2)

则x相上、下桥臂电流满足：

(3)

将式(1)中两式相减再除以2，结合式(3)整理得

(4)

为了描述的方便，引入了输出电压ux和等效阻抗Leq为

(5)

那么式(4)可以化简为

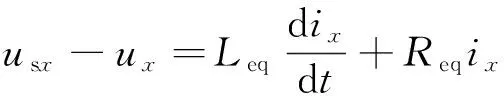
(6)

因为MMC相单元和上、下均具有严格的对称性，所以直流电流Idc在三相中均分，MMC的三相交流电流被上、下桥臂均分，所以MMC的相间环流主要包括两部分：直流部分和交流部分，直流部分主要起到功率传输的作用，交流部分主要包括2、4、6等偶数次谐波[13]。交流环流主要由于MMC三相上、下桥臂同时投入的子模块数目不一致和子模块电容电压不平衡引起的。如果各相所投入的子模块数目低于直流侧电压Udc，则产生正的环流成分补偿电压差异；相反各相上下桥臂所投入的子模块电容电压之和大于直流侧电压Udc，则产生负的环流成分。环流的具体表达式为

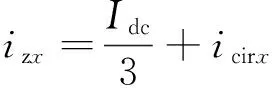
(7)

进一步可得上、下桥臂电抗器上的电压降为

(8)

结合式(2)、式(7)和式(8)可得

(9)

根据公式(6)和式(9)可以控制桥臂电感上的电压降(upcirx+uncirx)来抑制环流从而不会对输出电压和输出电流产生影响。

为了使MMC获得更好的稳态运行特性，MMC的内部动态参数比如子模块电容电压平衡和环流必须得到很好的控制。本文引入两种控制策略：模型预测控制与传统PI控制。同时为了研究MMC的外部动态特性，两种控制策略中均加入了输出电流控制。

2　模型预测控制

2.1模型预测控制基本原理

模型预测控制的主要思想是：在每个采样时刻，根据系统模型和MMC输出电压或电流的微分方程，使用模型预测控制预测出下一个采样时刻相应的电压或者电流值，然后通过与参考值进行比较，建立目标函数选择输出误差最小的开关组合状态，如图2所示为模型预测控制框图。

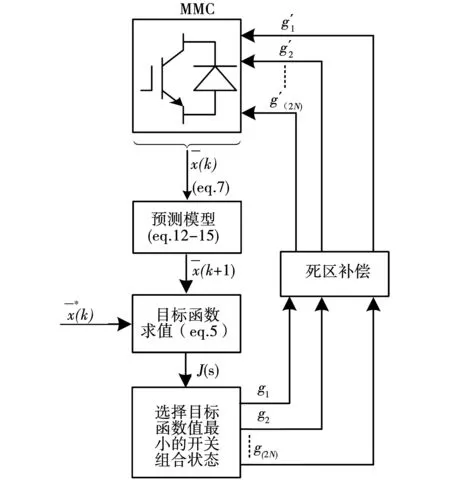
图2　模型预测控制流程框图Fig.2　Flow block diagram of model predictive control

模型预测控制主要分为以下三个步骤来实现:

1)根据MMC的数学模型，推导出其离散时间模型的表达式。

2)根据控制目标确定目标函数，模型预测控制包括三个控制目标：MMC交流侧输出电流控制，目的是控制MMC交流侧输出电流能够跟踪电流参考值；子模块电容电压均衡控制，目的是控制子模块电容电压能够稳定工作在其额定值附近；环流抑制，目的是抑制桥臂的环流交流分量，降低桥臂电流的畸变度。

3)在每个控制周期计算所有可能出现的投切组合下目标函数的值，选择使目标函数值最小的投切组合生成开关信号。

根据文献[14]的分析可得包含MMC交流侧输出电流、子模块电容电压和环流的目标函数为

λ4ns(k+1)。

(10)

其中，“*”表示参考值，λi(i=1,2,3,4)表示各控制目标的权重系数，权重系数的取值方法可以参考文献[15]。ns表示为了得到新的开关组合状态在采样周期k和采样周期k+1之间需要计算的开关组合数量。ns的计算表达式为

(11)

其中，g1,g2...g(2N)∈(0,1)表示各子模块的开关状态(当子模块处于1，2模式时，gi=1，当子模块处于3，4模式时，gi=0)。公式(11)的系数2是因为考虑到一个子模块中的两个IGBT的开关状态。

2.2建立系统数学模型

数学模型的建立对模型预测控制的执行具有关键性作用，模型的准确性直接影响着控制误差。仿真计算速度也主要依赖于所建模型的复杂程度。

(12)

由基尔霍夫电压定律可得如下方程式成立：

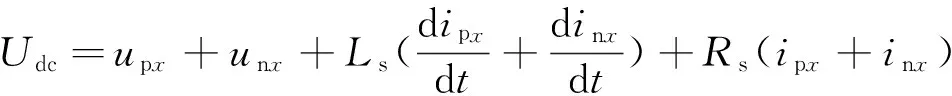
(13)

式(1)又可改写为

(14)

从式(13)和式(14)可知桥臂电抗Ls的电压降必须考虑在内，联合式(10)、式(13)和式(14)可得到如下状态矢量方程式成立：

(15)

式中，upx和unx是各桥臂所串联的子模块的开关函数，表示如下：

(16)

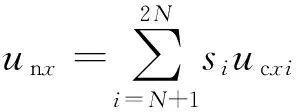
(17)

子模块的电容电压满足如下方程式：

(18)

为了提高计算速度，减少计算时间，采用了前置欧拉算法：

(19)

其中采样时间为Ts；由于桥臂电流改变的比较迅速，所以必须采用比较短的步长来预测电容电压，因此，方程式(19)被离散为如下方程式：

(20)

2.3死区补偿策略

子模块中的实际IGBT器件具有非理想开关特性,即具有开通和关断时间，且开通时间往往小于关断时间，为了避免桥臂直通，必须在同一子模块上下两个IGBT驱动信号之间设定“先断后通”的PWM开关死区。相对于开关周期来说，死区时间尽管很短，但是由于各桥臂级联的子模块较多，累计效应严重，MMC输出电压出现误差，进而导致MMC输出电流发生畸变。因此有必要对死区效应引起的电压损失进行有效补偿。

以图1中的某一子模块为例阐述死区补偿策略。当iSM>0时，若IGBT1驱动信号S1=1，IGBT2驱动信号S2=0，则IGBT1导通，IGBT2关断，则该子模块输出电压USM=Uc；当S1突变为0时，IGBT1关断，由D2续流，USM=0，此时即使S2=1，IGBT2依然不能导通，由此可见，当iSM>0时，子模块的输出电压USM仅有S1决定。同理，iSM<0时，USM仅有S2决定。

根据上述分析，当iSM>0时，保持S1不变，S2提前td关断并延迟td导通；当iSM<0时，保持S2不变，S1延迟td导通并提前td截止，即可使逆变器实际输出电压与理想输出电压一致。

引入死区补偿后的子模块上、下IGBT开关过程波形如图3所示。其中图3(a)为上下IGBT的理想驱动信号；图3(b)和图3(c)分别为iSM>0和iSM<0时的死区补偿原理；图3(d)为子模块理想输出电压USM波形图；图3(e)为采用本文提出的死区补偿方法后子模块实际输出电压波形，其中包括iSM>0和iSM<0两种情况。根据图3可知，将提出的死区补偿策略加入模型预测控制中(如图2)，可使子模块实际输出电压与理想输出电压一致，从而避免了死区效应给输出电压带来的影响。

3　传统PI控制算法

文献[9]中的MMC控制策略主要包括电容电压均衡控制和相间环流抑制模块，为了与模型预测控制算法相比较分析，文中还加入了MMC输出电流控制。这里传统PI控制方法分为三部分。

3.1外部输出电流控制

图3　死区补偿策略原理图Fig.3　Schematic diagram of dead-time compensation

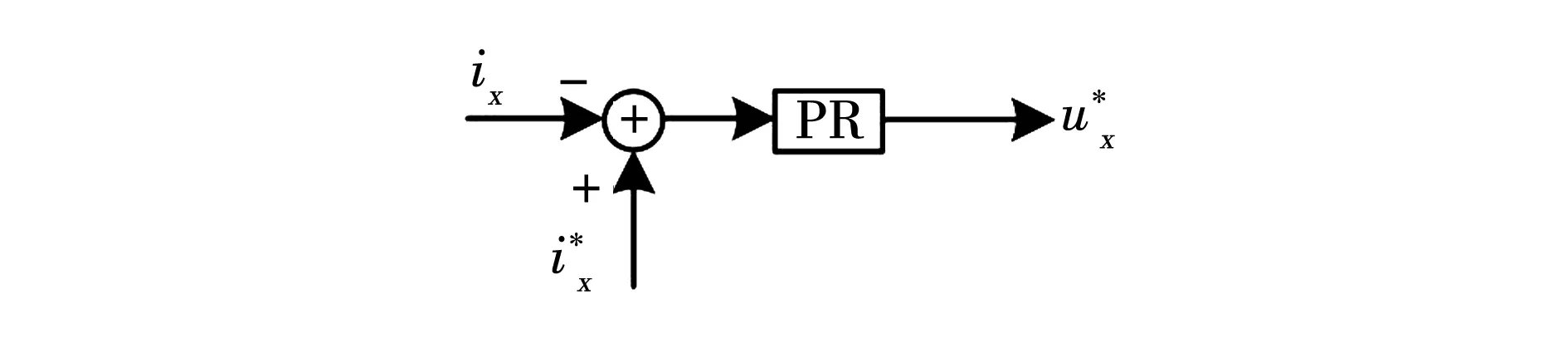
图4　输出电流控制框图Fig.4　Control diagram of output current

3.2能量均分控制

能量均分控制就是使各子模块电容电压的平均值跟踪它的参考值，从而控制MMC相间环流的大小使能量均匀的分配到各子模块中。如图5为能量均分控制的控制框图。

图5　能量均分控制框图Fig.5　Equipartition of energy control diagram

(21)

平均控制得到的电压调制参考值为

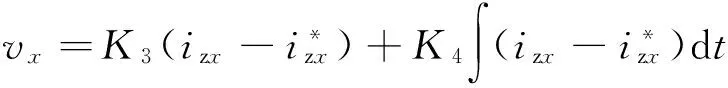
(22)

3.3电容电压均衡控制

电容电压均衡控制的目的就是使MMC各子模块电容电压跟踪其参考值，其控制框图如图6所示。对于x相上、下桥臂子模块的电压控制修正量为如下表达式：

(23)

图6　电容电压均衡控制框图Fig.6　Capacitor-voltages balancing control diagram

(24)

由于上、下桥臂中各含有N个子模块，且上、下桥臂中每个子模块的调制波表达式可以表示为

(25)

然后用得到的调制信号分别于相应的三角波比较得到需要的PWM控制信号，从而驱动IGBT的导通或关断。

4　实验验证与分析

为了研究MMC模型预测控制与传统PI控制策略的动态特性，特搭建了如图7所示的实验样机，由于受到实验室硬件条件和经费的限制，只搭建了各桥臂级联两个(N=2)子模块的三相MMC系统。直流侧母线电压为200V，也就是每个子模块电容电压维持在100V，所接负载为阻感负载；桥臂所串的电感值为2mH，每个子模块电容值为3 300μF。开关频率为1kHz。由于MMC模型预测控制计算复杂，为了减小计算负担，提高计算速度，本实验只采用单相MMC系统来比较分析两种控制策略的优缺点。其他两相主要为单相MMC系统提供恒定的直流侧母线电压。

图7　实验样机图Fig.7　Experimental prototype photo

4.1稳态特性比较分析

从图8(a)和9(a)输出电压实验波形可知，采用两种控制算法的MMC输出电压均为五电平；但是传统控制算法的输出电压脉冲比较规则，而模型预测控制算法的输出电压脉冲呈现不规则状态，其原因是由于模型预测控制采样时间不合适导致某些开关组合状态被遗漏。

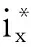
图8　模型预测控制稳态实验波形Fig.8　Steady experimental waveforms by model predictive control

两种控制算法都可以很好的抑制内部环流，且具有很好的稳态特性。尽管模型预测控制的环流在某些时间段不规则，但是环流的平均幅值比采用传统PI控制要小，抑制环流效果更明显，如图8(c)和图9(c)。

尽管两种算法均可使子模块电容电压处于均衡状态，但是控制效果却有显著差异。从图8(d)和图9(d)中可以看出，子模块电容电压中均包含高次谐波，但是模型预测控制的效果要比传统PI控制的效果好。不仅各桥臂的子模块电容电压处于均衡状态，而且同一相上、下桥臂的子模块平均电容电压也处于同一平衡状态；然而，传统PI控制的上、下桥臂的平均电容电压存在明显差异，这主要是因为控制器采样周期较长，增加了死区时间导致遗失某些开关状态；增加采样频率可以有效的解决上述问题。而模型预测控制由于增加了死区时间补偿，所以电容电压均衡效果较好。

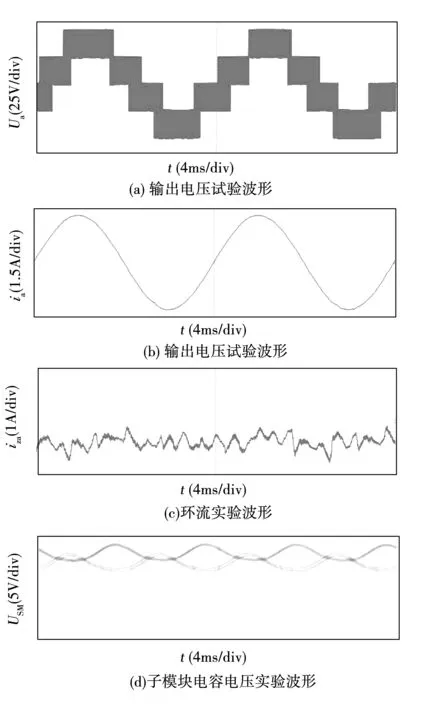
图9　传统PI控制稳态实验波形Fig.9　Steady experimental waveforms by traditional PI controller

4.2动态特性比较分析

当单相MMC系统处于稳态运行时输出电流参考值在1s时刻由5A突变为3A，得到的动态实验波形如图10、图11所示。根据图10可知采用模型预测控制时内部环流没有出现振荡，所以MMC系统表现出很好的稳定性。在1s时刻，输出电流ix经陡坡无超调地迅速跟踪参考值，所以具有很高的动态响应特性。然而如图11所示采用传统PI控制的动态响应相对较差，且出现了超调震荡，这同样是由于采样周期较长，死区时间的存在导致遗失了某些开关组合状态和参考值离散化不精确。模型预测控制补偿了死区时间，精确的预测可以减小超调，所以模型预测控制的动态特性要优于传统PI控制算法，这是模型预测控制的一个显著优点。

图10　模型预测控制动态实验波形Fig.10　Dynamic experimental waveforms by model predictive control

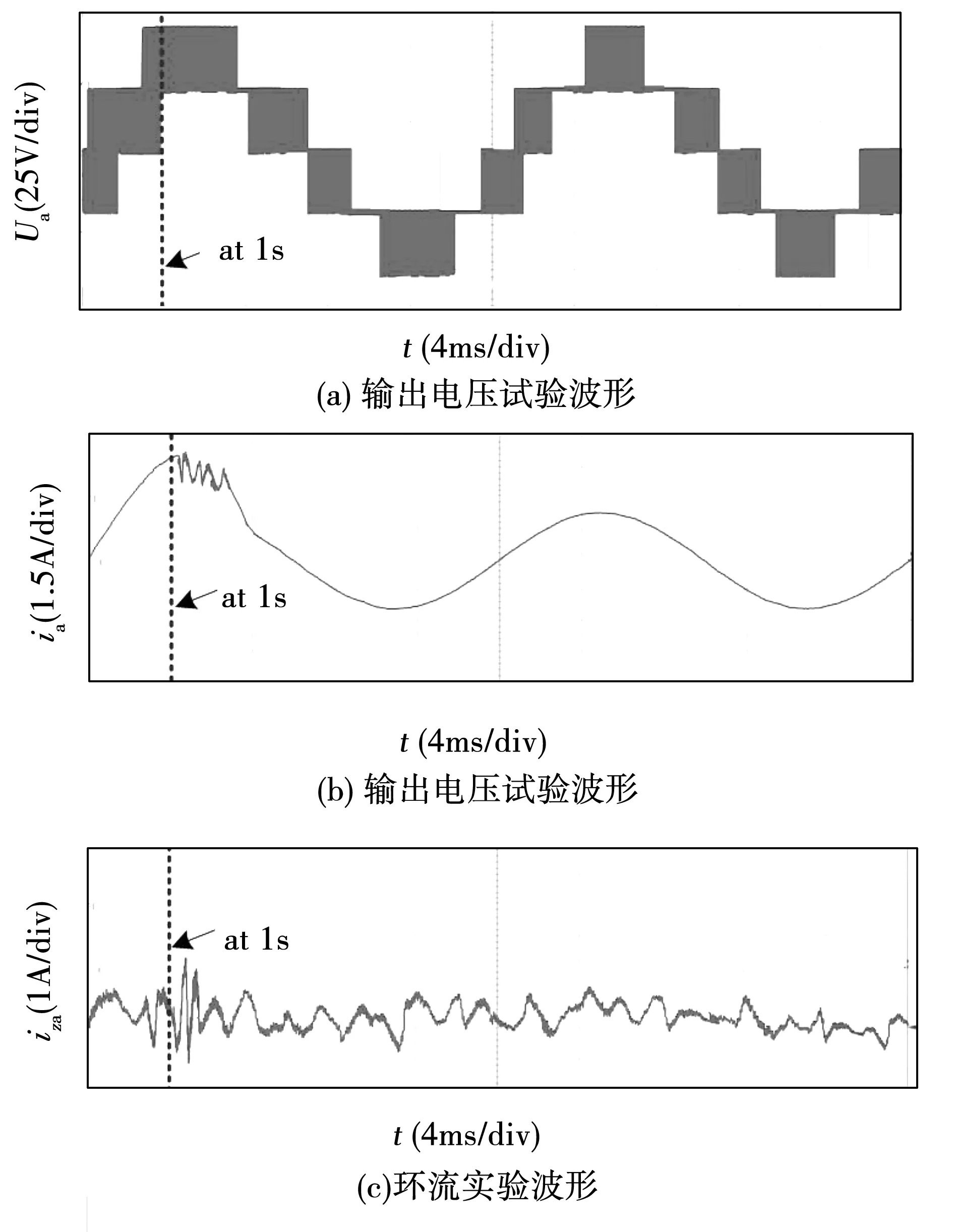
图11　传统PI控制动态实验波形Fig.11　Dynamic experimental waveforms by traditional PI controller

5　结　论

为了更好地控制MMC的内、外动态特性，本文研究了两种主流的MMC控制策略：模型预测控制和传统PI控制。首先深入分析了MMC的数学模型，然后研究分析模型预测控制与传统PI控制策略的工作原理，为了减小输出电流畸变，并在模型预测控制中引入了死区补偿。最后通过样机实验表明：模型预测控制结构简单所以具有很好的稳态特性；由于模型预测控制能知晓下一时刻的开关状态，并能预测最优的开关组合状态，所以比传统PI控制表现出更快的动态响应特性。但是模型预测控制的一个显著缺点是计算复杂，计算时间随子模块的数目呈指数增长。在控制性能与计算速度之间需要做一个妥协，模型预测控制不适合级联子模块多的MMC系统。

[1]LESNICAR A, MARQUARDT R．An innovative modular multilevel converter topology suitable for a wide power range[C]//IEEE Bologna Power Tech Conference．Bologna Italy.2003：545-546．

[2]汤广福，贺之渊，滕乐天，等．电压源换流器高压直流输电技术最新研究进展[J]．电网技术，2008，32(22)：39-45．

TANG Guangfu，HE Zhiyuan，TENG Letian，et al．New progress on HVDC technology based on voltage source converter[J]．Power System Technology，2008，32(22)：39-45.

[3]管敏渊，徐政．向无源网络供电的MMC型直流输电系统建模与控制[J]．电工技术学报，2013，28(2)：255-264．

GUAN Minyuan，XU Zheng．Modeling and control of modular multilevel based VSC-HVDC system connected to passive networks[J]．Transactions of China Electrotechnical Society，2013，28(2)：255-264．

[4]赵岩，胡学浩，汤广福，等．含模块化多电平换流器的分布式发电系统动态特性分析[J]．电网技术，2011，35(7)：42-47．

ZHAO Yan，HU Xuehao，TANG Guangfu，et al．Dynamic characteristics analysis of distributed generation system based on modular multilevel converters[J]．Power System Technology，2011，35(7)：42-47.

[5]ZHAO Y，HU X H，TANG G F，et al．A study on MMC model and its current control strategies[C]//IEEE International Symposium on Power Electronics for Distributed Generation Systems．Hefei，China：IEEE，2010：259-264．

[6]刘栋，汤广福，郑健超，等．模块化多电平换流器小信号模型及开环响应时间常数分析[J]．中国电机工程学报，2012，32(24)：1-7．

LIU Dong，TANG Guang，ZHENG Jianchao，et al．Small signal modeling and anaIysis of open-loop response time constant of MMC[J]. Proceedings of the CSEE,2012,32(24):1-8.

[7]Q. Tu, Z. Xu,J. Zhang．Circulating current suppressing controller in modular multilevel converter[C]//IEEE IECON 2010 36th Annual Conference on IEEE Industrial Electronics Society Glendale,USA.2010:3198-3202.

[8]G. BERGNA, E. BERNE, P. EGROT, P. Lefranc,et al. An energy-based controller for HVDC modular multilevel converter in decoupled double synchronous reference frame for voltage oscillation reduction[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2360-2371.

[9]M. HAGIWARA, H. AKAGI. Control and experiment of pulsewidth- modulated modular multilevel converters[J]. IEEE Transactions on Power Electronics,2009,24(7):1737-1746.

[10]CAO Mu, WANG Yue, CONG Wulong, et al.An optimization method of model preditive control for MMC[C]// The 20th Conference of China Power Supply Society,Hangzhou, 2013:301-306．

[11]CAO Mu, WANG Yue, LIU Pu, et al. Model predictive control of modular multilevel converter-based STATCOMs[C]//The 16th Conference of national electrical automation and electric control system of academic，Chengdu, 2013:52-56.

[12]Jiangchao Qin, Maryam Saeedifard. Predictive control of a modular multilevel converter for a back-to-back HVDC system[J]. IEEE Transactions on Power Delivery,2012,27(3):1538-1547.

[13]She X，Huang A，Ni X，et al．AC circulating currents suppression in modular multilevel converter[J]. IECON 2012-38th Annual Conference of IEEE Industrial Electronics，Montreal，QC，Canada，2012：190-194．

[14]Marcelo A. Perez, Jose Rodriguez, Esteban J. Fuentes. Predictive Control of AC-AC Modular Multilevel Converters[J]. IEEE Transactions on Industrial Electronics, 2012,59(7):2832-2839.

[15]P. CORTES, S. KOURO, B. LA ROCCA,et al. Guidelines for weighting factors design in model predictive control of power converters and drives[C]//ICIT2009,IEEE International Conference on Industrial Technology,Gippsland,VIC.2009:1-7.

(编辑：刘素菊)

Research on comparative analysis of MMC control strategies

LI Wei，LI Geng-yin

(State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources,North China Electric Power University,Beijing 102206, China)

Aiming at study the MMC control strategies, model predictive control was applied to MMC system. In order to achieve the better control results, dead-time compensation was introduced in model predictive control, and it made an in-depth analysis compared with the traditional PI controller. Finally, the prototype test results indicate that both control strategies can obtain good results on controlling MMC output voltages, currents, sub-model capacitor voltages and suppressing circulating currents. Although the output currents by model preditive control are not as good as that by traditional PI controller, the model preditive control has a great advantage on capacitor-voltages balancing. Besides, the dynamic performance of model preditive control is even superior to the considered PI control, due to the prediction of the future converter behavior.

modular multilevel converter; model preditive control; traditonal PI controller; dead-time compensation; circulating current suppressing; capacitor-voltage balancing control

2014-11-26

国家自然科学基金(51190103/E0704)

李威(1987—)，男，博士研究生，研究方向为多电平变换技术、柔性直流输电技术、新能源并网发电等；

李庚银(1964—)，男，博士，教授，博士生导师，研究方向为新能源发电、电力系统分析与控制、柔性输配电技术，电能质量等。

李威

10.15938/j.emc.2016.08.008

TM 72

A

1007-449X(2016)08-0055-09