基于改进GA-FFT综合含互耦效应的不等间隔阵列赋形方向图

游鹏飞　刘颜回*　黄　鑫　朱春辉　柳清伙（厦门大学电子科学系厦门361005）（杜克大学电气与计算机工程系达勒姆27708）



基于改进GA-FFT综合含互耦效应的不等间隔阵列赋形方向图

游鹏飞①刘颜回*①黄鑫①朱春辉①柳清伙②①
①（厦门大学电子科学系厦门361005）
②（杜克大学电气与计算机工程系达勒姆27708）

该文提出了一种虚拟的最小均方有源单元方向图展开方法，将不等间隔阵列的有源方向图展开为一个虚拟的均匀间隔阵列的若干单元辐射的叠加。通过该方法，对包含阵元耦合效应的不等间隔阵列方向图，可以使用快速傅里叶变换进行加速计算。并且，该文将这个方法与遗传算法（GA）相结合，得到一种改进的GA-FFT方法，可以应用于解决含阵元互耦的不均匀间隔阵列的赋形波束综合问题。最后，分别对不等间隔的偶极子阵列平顶方向图及微带阵列的余割平方方向图进行了综合，结果表明所提方法的有效性和优势。

不等间隔阵列；阵元互耦；FFT；波束赋形

1　引言

在阵列天线综合问题中，许多迭代综合方法如交替投影法、随机优化算法等，具有广泛的应用［13］-。在这些方法中，遗传算法（Genetic A lgorithm，GA）由于其鲁棒性和普适性，被广泛地用来搜索全局最优解。然而同其他迭代算法一样，遗传算法也需要大量反复地计算阵列方向图，计算时间较长。因此，对于迭代综合方法而言，加快阵列方向图的计算，可以显著降低这些方法的计算复杂度。对等间隔阵列而言，假定各单元具有相同的单元方向图的情况下，可以采用快速傅里叶变换（Fast Fourier Transform，FFT）来加速阵因子的计算，如GA-FFT方法［4］。近年来，一些学者又将这些方法与非均匀快速傅立叶变换（Non-Uniform Fast Fourier Transform，NUFFT）相结合，将之推广应用于不等间隔阵列的阵因子计算［58］-，其中GA-NUFFT［8］方法就是主要代表之一。然而，这种基于NUFFT的阵列综合算法依然只适用于具有相同单元方向图的情况，不能考虑实际阵列中阵元互耦等因素导致的单元方向图的差异影响。

众所周知，采用有源单元方向图来计算阵列方向图，可以包含阵元耦合以及阵列安装环境的影响［9，10］。然而，由于有源单元方向图各不相同，无法提取阵列因子，不能应用FFT或NUFFT来加速。为了克服这一问题，许多学者提出了一些近似方法。在文献［11］中，将等间隔直线阵列的单元分为两类：阵中单元和边沿单元。阵中单元享有共同的单元方向图，可以采用FFT计算这部分单元对总阵列方向图的贡献，边沿单元方向图各不相同，则需要直接求和计算。该方法比较适合于电大规模的等间隔阵列问题。文献［12］将每一个有源单元方向图看成由整个阵列耦合激励的阵因子与单元孤立存在时的方向图的乘积。尽管该方法适用于任意间隔阵列，但由于需要求解每一个有源单元方向图对应的所有阵元的耦合系数，需要较高的计算复杂度。

最近，文献［13］提出了一种最小均方有源单元方向图展开（Least-Square Active Element Pattern Expansion，LS-AEPE）方法。该方法将有源单元方向图看成是阵列中部分相邻单元辐射的叠加，对每一个有源单元方向图而言，仅需要求解少数几个单元的耦合系数。为减少这种近似误差，耦合系数由最小均方误差准则获得。应用该方法，等间隔阵列的方向图可以使用标准的FFT加速，并且可以包含阵元互耦以及安装环境的影响。本文将该方法推广应用于含阵元互耦效应的不等间隔阵列的赋形波束综合问题。与文献［13］不同，针对实际的不等间隔阵列情况，我们需要构造一个虚拟的等间隔阵列，将每一个有源单元方向图看成是虚拟阵列中若干等间隔单元的辐射叠加形成，且虚拟单元的激励系数也由最小均方误差准则给出。我们称这个方法为虚拟的最小均方有源单元方向图展开方法。并且，本文将这个方法与GA方法结合，得到一种改进的GA-FFT方法，可以有效地对含阵元互耦的不等间隔阵列进行优化。最后使用该方法综合了不等间隔偶极子阵列的平顶方向图以及不等间隔微带阵列的余割平方方向图，结果证明了本文方法的有效性和优势。

2　不等间隔阵列有源单元方向图的最小均方误差展开

以N元非均匀间隔线阵为例，阵元分布在X轴上，阵列方向图可以表示为

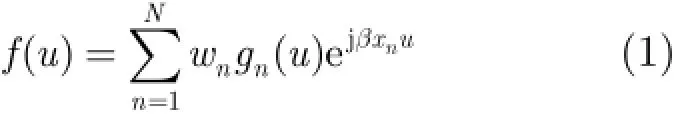
为应用FFT加速计算，我们将实际的不等间隔阵列插值为虚拟的等间隔阵列，如图1所示。实际阵列中的每个有源单元方向图可以视为其邻近位置的若干个虚拟单元组成的虚拟子阵辐射造成的。这样实际的不等间隔阵列中的每个有源单元方向图可以展开为虚拟的等间隔阵列中若干个邻近位置的虚拟单元方向图的加权叠加。如图1所示，在第1个线框中的5个等间距虚拟阵元组成的虚拟子阵用来插值实际阵列中的第1个阵元，即用该虚拟子阵辐射的方向图来近似第1个有源单元方向图。以此类推，相同的方法依次处理实际阵列中每一个有源单元方向图。

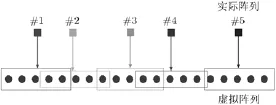
图1　用虚拟的等间隔阵列展开实际阵列的有源单元方向图

因此，我们有

为减少式（2）中有源方向图展开的近似误差，虚拟单元的激励系数nqc通过求解最小化均方误差问题得到：

其中

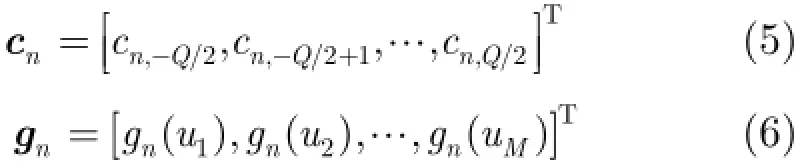
上述问题的最小均方误差解为n=c因此该方法被称为虚拟的有源单元方向图的最小均方展开方法（Virtual Least-Square Active Element Pattern Expansion，VLS-AEPE）。

3　改进的GA-FFT综合具有阵元互耦的不等间隔阵列赋形方向图

将式（2）代入式（1），我们可以重写阵列方向图的表达式为

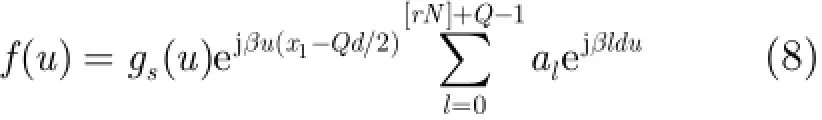
其中

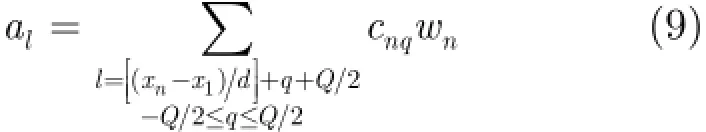
在u域上均匀采样，则可以直接应用标准FFT来实现式（8）的加速计算。可见，通过上述处理后，可以实现在考虑阵元互耦情况下不等间隔阵列方向图的FFT加速。

结合不同的阵列综合策略，上述方法可以应用到不同的阵列综合问题。这里，我们考虑非均匀间隔线阵的赋形功率方向图综合问题。赋形功率方向图的综合是一个高度非线性的问题，我们应用遗传算法（GA）来搜索阵元激励的全局最优解［4］。在GA算法中，每一个个体（或者染色体）关联一组阵列激励。对于N元阵列，每组优化变量具有2N的维度。其中，前N个元素代表阵列激励的幅度，采用实数编码，取值范围为［］0，1；后N个元素代表阵列激励的相位，采用实数编码，取值为［］，-ππ。对于方向图综合问题，我们关心的是阵元激励幅度和相位分布的相对大小，而不是它们的绝对值。因此，对位置固定的N元阵列而言，其实际自由度为2 2N-。在赋形功率方向图优化过程中，我们设定的目标函数为最小化赋形区域上功率方向图与期望函数的误差，并增加不同区域的方向图边界控制以及最大激励幅度比的约束条件。数学表述为

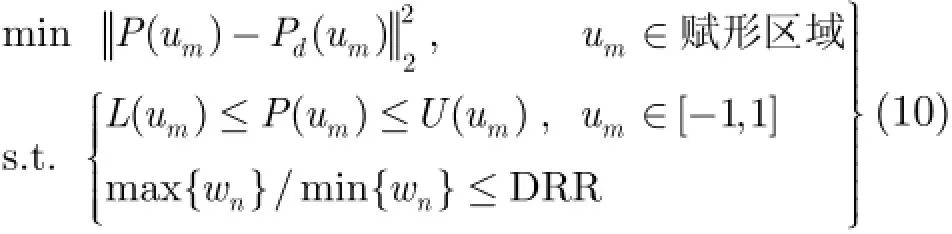
在GA综合算法中，假定每一代进化中的每一个个体均需要计算阵列方向图。对于M个采样点的一次阵列方向图计算，对式（1）直接求和需要MN次复数乘法，而应用VLS-AEPE方法可借用FFT对式（8）进行计算，仅需要次复数计算（假定使用基2的FFT算法，其中表示对x向上取整）。设置图2显示了这两种方法计算阵列方向图所需的复乘数目。可见，当阵元数目N大于7时，VLS-AEPE FFT方法比直接求和方法需要更少的复乘次数，且随着N的增大，这种计算优势更为明显。如果使用混合基的FFT算法，比如基2和基4的混合算法，还可以进一步提高计算效率。由于GA算法需要大量多次进行阵列方向图计算，应用VLS-AEPE FFT方法可以大大提高计算效率。

4　数值结果

4.1平顶方向图综合

考虑一个12元非均匀间隔的线阵，阵元位置由FBMPM［14］方法得到。在文献［14］中，FBMPM方法假设单元为理想点源，得到了满足边界的平顶赋形方向图。然而在实际阵列中，由于单元互耦效应的存在，FBMPM方法优化的权值在实际全波仿真或测试中得到的结果往往存在较大的误差。本文考虑单元天线为工作频率在1GHz的偶极子天线，阵列模型如图3所示。该阵列的有源方向图可以使用全波仿真软件如HFSS得到。

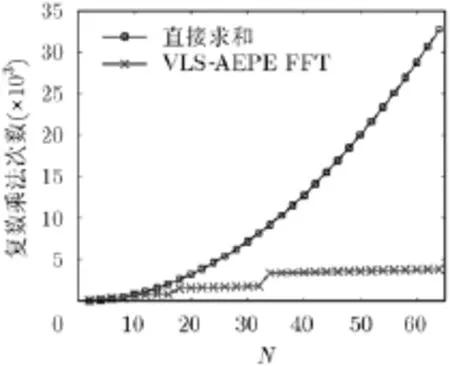
图2　计算阵列方向图所需的复乘次数与阵列规模的关系

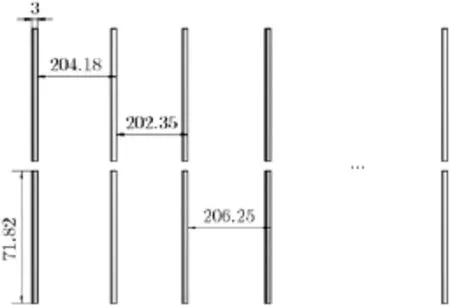
图3　 12元不等间隔偶极子天线阵列（mm）

为了评估VLS-AEPE方法用于展开该阵列有源单元方向图的精度，我们定义误差为

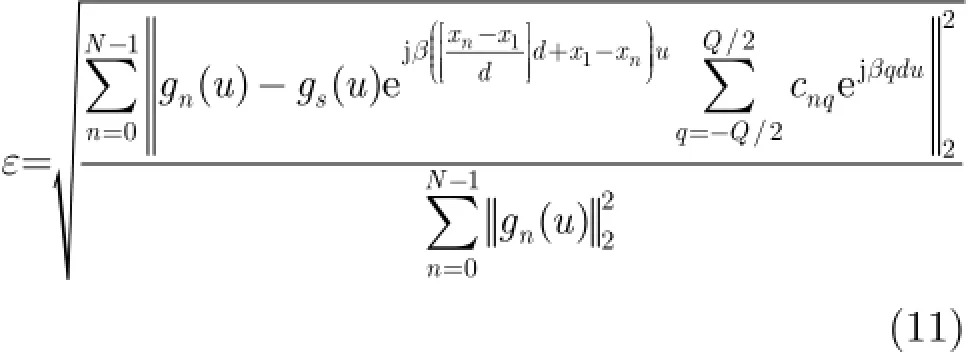
图4显示了误差ε与参数d和Q的关系。由图4可见，对于固定的d，Q越大，误差就越小；对于固定的Q，d减小也会降低误差。但是当d≤0.35λ时，减小d并不能降低误差。这是由于在固定Q的情况下，d减小意味着用来展开有源方向图的虚拟子阵的间距变小，同时所用的口径也越小了，抵消了小间距带来的精度改善。在这个例子中，我们取d= 0.35λ，Q=6。这时，12元含耦合的不等间隔线阵可以变换为30元虚拟的等间隔线阵。采用虚拟子阵展开后，可以采用FFT来计算阵列方向图，并使用GA算法对激励和相位进行优化，使得综合的方向图满足波束赋形和副瓣控制的要求。如图5所示，使用点源假设的FBMPM方法综合的激励，在用于图3所示的偶极子阵列后，由于阵元互耦的存在，所得方向图在低副瓣电平区域不能满足-40 dB的要求。而采用本文方法优化后，所得阵列方向图完全满足所给定的副瓣及波束赋形要求。另外，我们约束了最大激励幅度比为3.4，略小于文献［14］中给出的激励幅度比3.6。

由图2可知，阵列规模越大，VLS-AEPE FFT对于阵列方向图计算的加速效果越显著。因此，考虑扩大阵列规模，对一个41元不等间隔的线阵综合平顶方向图，如图6所示。单元天线仍然选用图3所示的偶极子天线，单元位置由文献［15］给出。采用本文提出的GA-VLS AEPE FFT方法对激励进行优化，考虑了单元方向图以及互耦效应，所得阵列的方向图与GA-直接求和方法得到的结果吻合得比较好，均严格满足期望的方向图边界：赋形区域波束宽度和波纹响应幅度分别为40°和0.3 dB，副瓣区域电平控制在-30 dB以下。

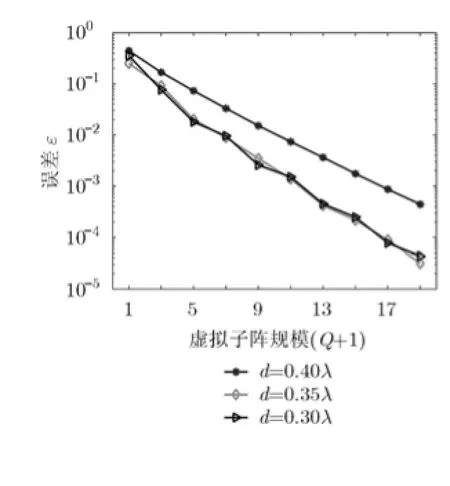
图4　 VLS-AEPE方法的误差ε与参数d，Q的关系

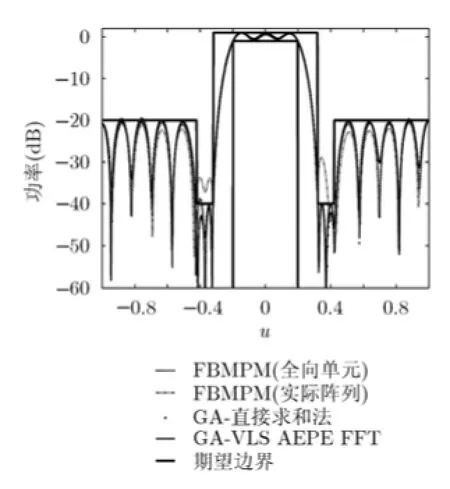
图5　 12元不等间隔线阵平顶方向图综合结果

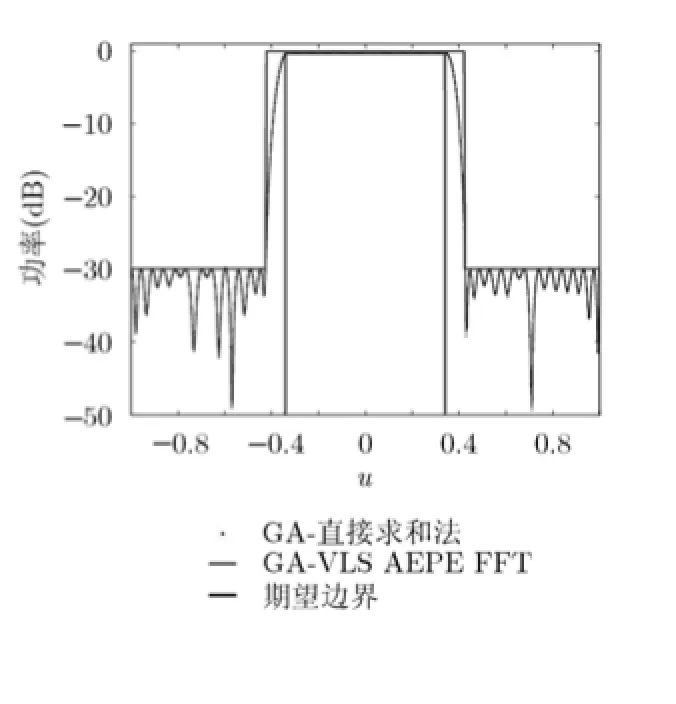
图6　 41元不等间隔线阵平顶方向图综合结果

4.2余割平方方向图综合

考虑对一个13元不等间隔的线阵综合余割平方方向图。假定单元天线为工作频率在2.45 GHz的微带天线，单元位置由文献［16］给出，阵列模型如图7所示。如果采用文献［16］给出的激励，由于微带单元方向图的调制以及相邻单元耦合的存在，所得阵列的方向图超出期望的方向图边界，如图8所示。而采用本文提出的GA-VLS AEPE FFT方法对激励进行优化后，满足了波束赋形和副瓣控制的要求，修正了直接使用文献［16］给出的激励，由于未考虑单元方向图以及互耦而产生的误差。另外，我们约束了激励幅度比为5.1，而文献［16］中所得结果的激励幅度比为9.6。

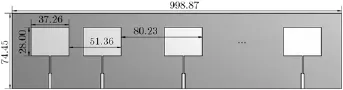
图7　 13元不等间隔微带阵列（mm）

5　结束语

本文针对不等间隔阵列，提出了一种虚拟的最小均方有源单元方向图展开方法。可以在考虑阵元电磁耦合的情况下，对阵列方向图计算进行FFT加速。将该方法与遗传算法相结合，得到了一种改进的GA-FFT方法，可以对考虑互耦的不等间隔阵列进行方向图赋形综合。最后，我们对不等间隔的偶极子阵列进行平顶方向图综合，对不等间隔的微带阵列进行了余割平方方向图综合，所得结果严格满足预先设定的波束赋形及副瓣区域的要求，证明了本文方法的有效性。

另外，本文方法可以进一步推广到考虑安装平台对天线阵列的影响。对于安装在平台上的天线阵列，可以采用测试的有源单元方向图，运用本文方法依然具有可行性。

［1］WANG X，ABOUTANIOS E，and AM IN M G.Thinned array beampattern synthesis by iterative soft-thresholdingbased optim ization algorithm s［J］.IEEE Transactions on Antennas and Propagation，2014，62（12）:6102-6113.doi:10. 1002/MOP.10823.

［2］赵宜楠，张涛，李风从，等.基于交替投影的M IMO雷达最优波形设计［J］.电子与信息学报，2014，36（6）:1368-1373.doi: 10.3724/SP.J.1146.2013.01198.

ZHAO Y N，ZHANG T，LI F C，et al.Optim al waveform design for M IMO radar via alternating projection［J］.Journal of Electronics&Information Technology，2014，36（6）: 1368-1373.doi:10.3724/SP.J.1146.2013.01198.

［3］于波，陈客松，朱盼，等.稀布圆阵的降维优化方法［J］.电子与信息学报，2014，36（2）:476-481.doi:10.3724/SP.J.1146. 2013.00526.

YU B，CHEN K S，ZHU P，et al.An optim um method of sparse concentric rings array based on dimensionality reduction［J］.Journal of Electronics&Information Technology，2014，36（2）:476-481.doi:10.3724/SP.J.1146. 2013.00526.

［4］WANG L L，FANG D G，and SHENG W X.Comb ination of Genetic A lgorithm（GA）and Fast Fourier Transform（FFT）for synthesis of arrays［J］.M icrowave and Optical Technology Letters，2003，37（1）:56-79.doi:10.1002/MOP.10823.

［5］LIU Q H and NGUYEN N.An accurate al，gorithm for NonUniform Fast Fourier Transform s（NUFFT s）［J］.IEEE M icrowave and Guided W ave Letters，1998，8（1）:18-20.doi: 10.1109/75.650975.

［6］YANG K，ZHAO Z Q，and LIU Q H.Fast pencil beam pattern synthesisof large unequally spaced antenna arrays［J］. IEEE Transactions on Antennas and Propagation，2013，61（2）:627-634.doi:10.1109/TAP.2012.2220319.

［7］LIU J Z，ZHAO Z Q，YANG K，et al.A hybrid optim ization for pattern syn thesis of large antenna arrays［J］.Progress In Electromagnetics Research，2014，145:81-91.doi:10.2528/ PIER13121606.

［8］JIANG M L，CHEN R S，ZHOU L，et al.Synthesis of arrays w ith Genetic A lgorithm（GA）and Nonuniform Fast Fourier Transform（NFFT）［C］.Asia-Pacific M icrowave Conference Proceedings（APMC），Suzhou，China，2005，4:2.doi:10. 1109/APMC.2005.1606885.

［9］POZAR D M.The active element pattern［J］.IEEE Transactions on Antennas Propagation，1994，42（8）: 1176-1178.doi:10.1109/8.310010.

［10］POZAR D M.A relation between the active input im pedance and the active elem ent pattern of a phased array［J］.IEEE Transactions on Antennas and Propagation，2003，51（9）: 2486-2489.doi:10.1109/TAP.2003.816302.

［11］KELLY D F and STUTZMANW L.Array antenna pattern modeling methods that include mutual coupling effects［J］. IEEE Transactions on An tennas and Propagation，1993，41（12）:1625-1632.doi:10.1109/8.273305.

［12］STEYSKAL H and HERD J S.Mutual coup ling compensation in small array antennas［J］.IEEE Transactions on Antennas and Propagation，1990，38（12）:1971-1975.doi: 10.1109/8.60990.

［13］YOU P F，LIU Y H，HUANG X，et al.Efficient phase-only linear array synthesis including coup ling effect by GA-FFT based on least-square active element pattern expansion method［J］.Electronics Letters，2015，51（10）:791-792.doi: 10.1049/EL.2015.0431.

［14］LIU Y H，NIE Z P，and LIU Q H.A new method for the synthesis of non-uniform linear arrays w ith shaped power patterns［J］.Progress In Electromagnetics Research，2010，107: 349-363.doi:10.2528/PIER10060912.

［15］WANG F，BALAKRISHNAN V，ZHOU P Y，et al.Op timal array pattern synthesis using sem idefinite p rogramm ing［J］. IEEE Transactions on Signal Processing，2003，51（5）: 1172-1183.doi:10.1109/TSP.2003.810308.

［16］FUCHSB.Synthesis of sparse arraysw ith focused or shaped beam pattern via sequential convex optim izations［J］.IEEE Transactions on Antennas and Propagation，2012，60（7）: 3499-3503.doi:10.1109/TAP.2012.2196951.

游鹏飞：男，1986年生，博士生，研究方向为阵列综合与设计.

刘颜回：男，1983年生，副教授，博士生导师，研究方向为天线设计与阵列理论、阵列信号处理.

黄鑫：男，1991年生，硕士生，研究方向为阵列综合与设计.

Modified GA-FFT for Synthesizing Shaped Pattern of Unequally Spaced A rray in Presence of M utual Coup ling

YOU Pengfei①LIU Yanhui①HUANG Xin①ZHU Chunhui①LIU Qinghuo②①
①（Department ofElectronic Science，Xiam en University，Xiamen 361005，China）
②（Department ofElectrical and Computer Engineering，Duke University，Durham 27708，USA）

A new Virtual Least-Square Active Element Pattern Expansion（VLS-AEPE）method is presented in this paper，w hich considers each active elem ent pattern of an unequally spaced array as the one radiated by some of equally spaced elem ents of a virtual array.Using the help of thism ethod，the pattern of an unequally spaced array includingmutual coupling can be efficiently calculated by FFT.In addition，thismethod is combined w ith the Genetic A lgorithm（GA）to dealwith the shaped pattern synthesis prob lem for unequally spaced linear arrays. Two synthesis experiments including the synthesis of flat-top pattern for an unequally spaced dipole array and the synthesis of cosec-squared pattern for an unequally spaced m icrostrip array are conducted to verify the effectiveness and advantages of the proposed algorithm.

Unequally spaced linear array；E lem ent mutual coup ling；FFT；Shaped pattern synthesis

s:The National Natural Science Foundation of China（61301009），The Fundamental Research Funds for the Central Universities（20720160081）

TN 820

A

1009-5896（2016）08-2107-06

10.11999/JEIT 151189

2015-10-29；改回日期：2016-04-08；网络出版：2016-05-24

刘颜回yanhu iliu@xm u.edu.cn

国家自然科学基金（61301009），中央高校基本科研业务费（20720160081）