基于二维不可分小波变换的矩不变量

刘　斌　高　强（湖北大学计算机与信息工程学院武汉430062）



基于二维不可分小波变换的矩不变量

刘斌高强*
（湖北大学计算机与信息工程学院武汉430062）

寻找相对于尺度、平移、旋转不变的小波不变量是多尺度分析在模式识别中应用的关键性问题。该文利用基于统计的不变矩这一理论和应用上都比较成熟的方法，将图像有限个尺度的小波近似系数和图像不变矩联系起来，从而给出了一种小波矩不变量，得到了比较完善的理论和实验结果。同时指出了该理论方法在实际应用中所需注意的地方，最后简要阐述了多尺度分析与不变矩的应用关系。

模式识别；多尺度分析；2维不可分小波；不变矩；平滑性；近似系数

1　引言

在信号及图像处理中，多尺度分析的思想由来已久，文献［1］提出了基于LAPALACE金字塔式的分解从而进行多尺度的特征提取与识别，但金字塔分解后各层数据的相关性影响了它的性能。随着小波理论［2］的发展，文献［2］基于小波的塔式分解算法使各层的细节相对独立而具有良好的应用。由小波及其多分辨率分析理论［3，4］可知，一幅图像可分解为按尺度分辨率逐级降低的近似信息和细节信息，各个尺度的细节信息表示它不同的物理结构，而近似信息表示其总体轮廓，基于此理论上我们可从大尺度上分析图像然后逐层细化识别，即所谓多尺度识别。多尺度识别的关键是找到待识别模式在有限个尺度下相对于平移、尺度、旋转变化的不变量，这正是不变矩所具备的特性，据此可利用不变矩理论表征这种不变量。

不变矩理论从1维到多维都有比较成熟的理论和方法，可从目标图像中提取不变矩作为特征进行目标的正确识别和图像匹配等方面的应用［5］。文献［6］利用代数不变量理论首次给出了2维不变矩的表示，其中阶数小于3的7个具有平移、旋转和尺度不变性的不变矩是应用的基础。矩（中心矩）实际上反映物体灰度相对于质心的统计分布情况，计算量大而且高阶矩受噪声影响较大一直困扰着矩方法，这是矩对信号进行全局化处理造成的，为减小计算量人们也提出了一些改善的方法［7］。另一方面，图像上物体可由各个不同相关联的结构组成，而图像的灰度信息只在各结构之间局部地相关着，而与其较远的结构关系不大，就单个图像像素而言它也只与附近一定范围内的像素具有较强相关性，而与其距离越远的像素越无相关性以至于几乎不相关。受Fourier变换局部化的启示，希望能将反映相关信息的矩方法也分层局部化，具有“数学显微镜”之称的局部化分析工具小波是一种理想的选择。

在Fourier分析的基础上发展起来的小波分析在1维及其张量积形式情形下都有比较成熟的理论和方法，但利用张量积小波对2维图像及更高维信号进行处理，由于其人为的方向性的处理方式显然具有很大的缺陷。由此产生了2维非张量积的小波理论，并已有一些相关的理论和应用研究［810］-，但其总体的理论和应用远不及1维小波那样成熟。文献［11］阐明了1维及2维张量积的小波矩不变量。本文在现有2维非张量积（不可分）小波理论的基础上，结合不变矩的理论和方法从理论上进行推广和拓展得到了在2维不可分情形下的小波矩不变量。同时进行了相应的数值验证工作。此矩不变量比基于原图像的矩值计算量大幅减小，同时继承了不可分小波变换和不变矩的一些优点而使其能够更好地应用于模式识别领域。

2　　2维不可分小波变换及其多分辨率分析理论

2维不可分的多分辨率分析可从相应的1维的多分辨率分析作推广而得，具体是指在中有一串嵌套的闭子空间逼近序列满足下列条件：

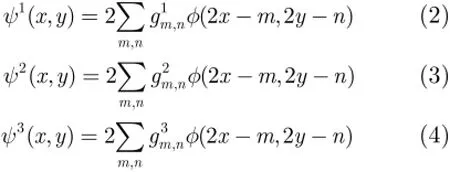
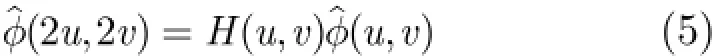
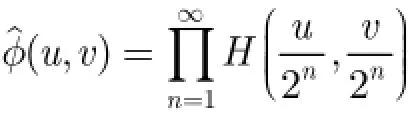
同理分别对式（2）、式（3）、式（4）两边作Fourier变换，可得

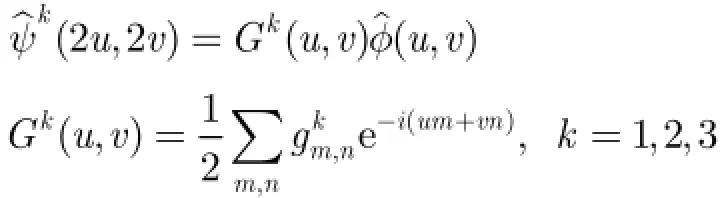
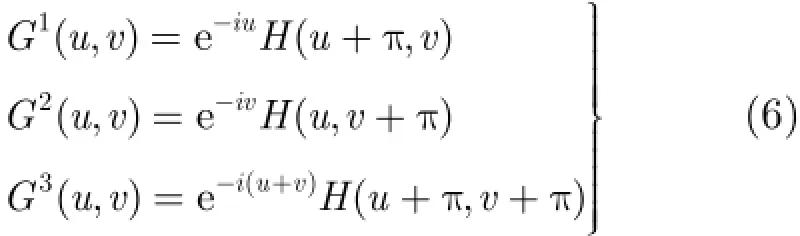
由以上分析可知（，）H u v的构造是多分辨率分析的关键，给定共轭滤波器（，）H u v满足：

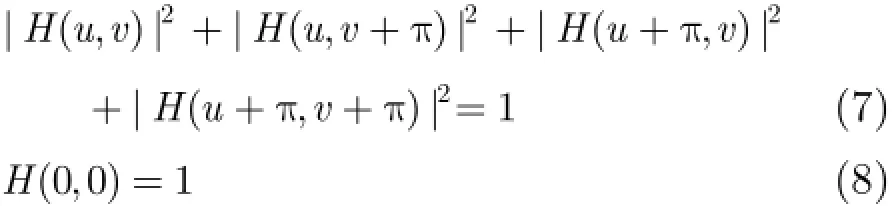
实际设计滤波器时都对（，）H u v有平滑性的要求，设（，）H u v可被分解为［14］

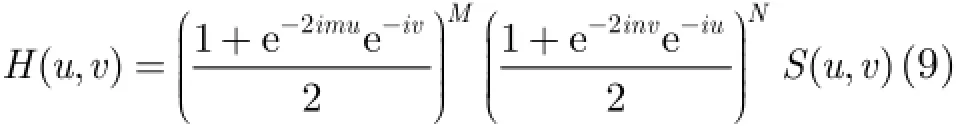
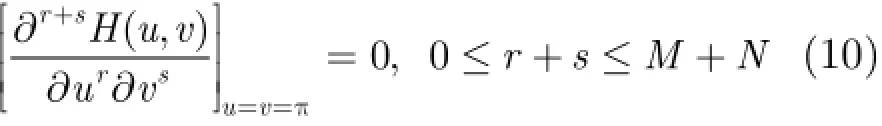
证明由2维小波分析理论，（1）中的等式显然是成立的，以下简要证明（2）中结论。

3　矩与小波不变矩

2维平面上灰度图像（，）f x y的p q+阶几何矩［6］的定义为

当（，）f x y在-x y平面上的有限区域内非零且分段连续时，pqm与（，）f x y互相唯一确定。矩的特定代数式在图像平移、旋转、尺度变化时保持定值，称为不变矩。把坐标原点移至（，）f x y的质心，再除以一个尺度因子，可得到p q+阶中心化规格矩：

而由中心化规格矩可以组合表示出文献［6］中的7个具有平移、旋转、尺度变化的不变矩，这里不再列出。在文献［6］工作的基础上，文献［15］进一步给出了离散情况下各阶矩的计算方法，另外为保证离散情况下不变矩的尺度不变性，文献［16］对归一化的中心距进行了修正，实际情况下可借鉴这些方法以取得更好的应用效果。对函数（，）f x y作2维Fou rier变换可得（，）F u v对等式两边同时对u求 p阶偏导，再接着对v求q阶偏导，最后令有

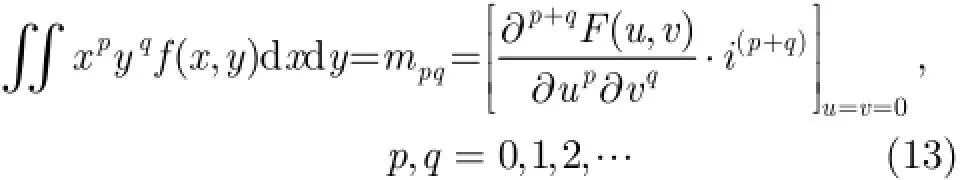
由式（13）和引理1可得引理2。

引理2如果（，）H u v在（0，0）点有M N+次平滑性，则

（1其下同；

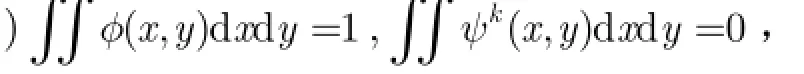
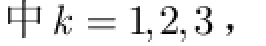
（2）

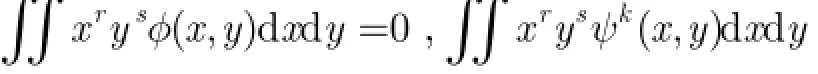
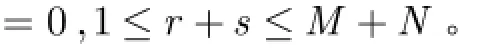
定理1如果共轭滤波器（，）H u v在（0，0）点有M N+次平滑性，将（，）f x y按（，）H u v构造的尺度函数及小波函数作小波展开，是其近似系数，令表示基于2维不可分小波变换近似系数的p q+阶小波矩，则

在设计共扼滤波器（，）H u v时，如果使（，）H u v在零点有M N+次平滑性，那么按照（，）H u v得到的尺度函数和小波函数将2维图像（，）f x y在其上分解后产生的任一层次j的近似系数，理论上可无误差地表达阶次不大于M N+的矩值，式（14）中不出现细节系数。这表明图像作2维不可分小波分解后，它的有限个视觉不变量将始终保留在任一层次的近似中而与任一层的细节无关，即得到了基于近似系数的小波矩不变量。这种基于近似系数的小波矩不变量，通过作平移、规格化及类似7个几何不变矩的代数组合变换，就可得到基于近似系数的小波不变矩。这样的小波不变矩有3个基本优点：其一，由于近似系数只为原始图像数据量的1/4甚至更小（分解尺度增加时），故基于小波分解近似系数的矩值计算复杂性将大幅减小；其二，如果原始图像存在噪声，对图像进行2维不可分小波分解后噪声主要存在于细节系数中，这样基于少量噪声的近似系数计算得到的矩值比通过原始噪声图像计算的矩值应更准确和更能表征物体的特征，而有利于模式的正确识别；其三，小波变换可以获取图像中物体的细节结构特征，而在模式识别的理论和方法中，基于统计的不变矩能很好地对模式的特征信息进行描述［17］，故将小波变换和不变矩方法结合起来可充分利用两者的优点，为进一步提出相关高效的模式识别应用算法奠定了基础［18］。

实际应用中逼近层j和平滑性M+N的值是有限制的，尽管从原则上增大逼近层j和平滑性M+N能以较小的计算代价获得更多的矩不变量信息，但在实际应用中将受到物体大小和Gibbs效应的影响。总地来说，为保证足够的计算精度以利于精确识别，逼近层j应满足为图像尺寸，对此文献［6］有较为详细的分析；另一方面，图像小波分解过程中的卷积会存在破坏边界的Gibbs效应，这将影响待识别物体从背景的分割，而分割的好坏直接影响矩不变量的计算。为减少Gibbs效应的影响，M+N值也不能太大。

4　实验与结果分析

本文利用设计得到的2维不可分小波滤波器在Matlab8.0平台上对Lena灰度图像进行分解后，计算其基于近似系数的矩不变量，结果列于表1。

理论上说阶数小于5的矩值在任一层得小波逼近系数中应保持定值，而且阶数越小其误差值越小，实验结果很好地反映了这一点。当然，随着矩阶数的增高和逼近层数的加大，误差也逐渐增大，这是物体尺寸和Gibbs效应的影响，已在第3节中指出。

为验证式（14）的抗噪性能，本文对Lena图像加噪声（见图1）后同样利用2维不可分滤波器对噪声图像进行分解求其不同尺度下的矩不变量，将其与按式（11）计算得到的无噪声图像原始准确矩值比较，得出表2数据。

由表2的矩值误差数据明显可知第0层的矩值误差是最大的，而随着分解层数的增加近似系数受噪声影响越来越小使其矩值误差相对准确值的误差越来越小，正如第3节所述这是由于小波变换将原图像的大部分噪声分解到细节系数中，而近似系数所含噪声较少的缘故。当然随着尺度的进一步增大，由于物体尺寸和Gibbs效应及其他原因导致的误差增加导致相对准确矩值的误差值有所变大，但总体成减小的趋势。

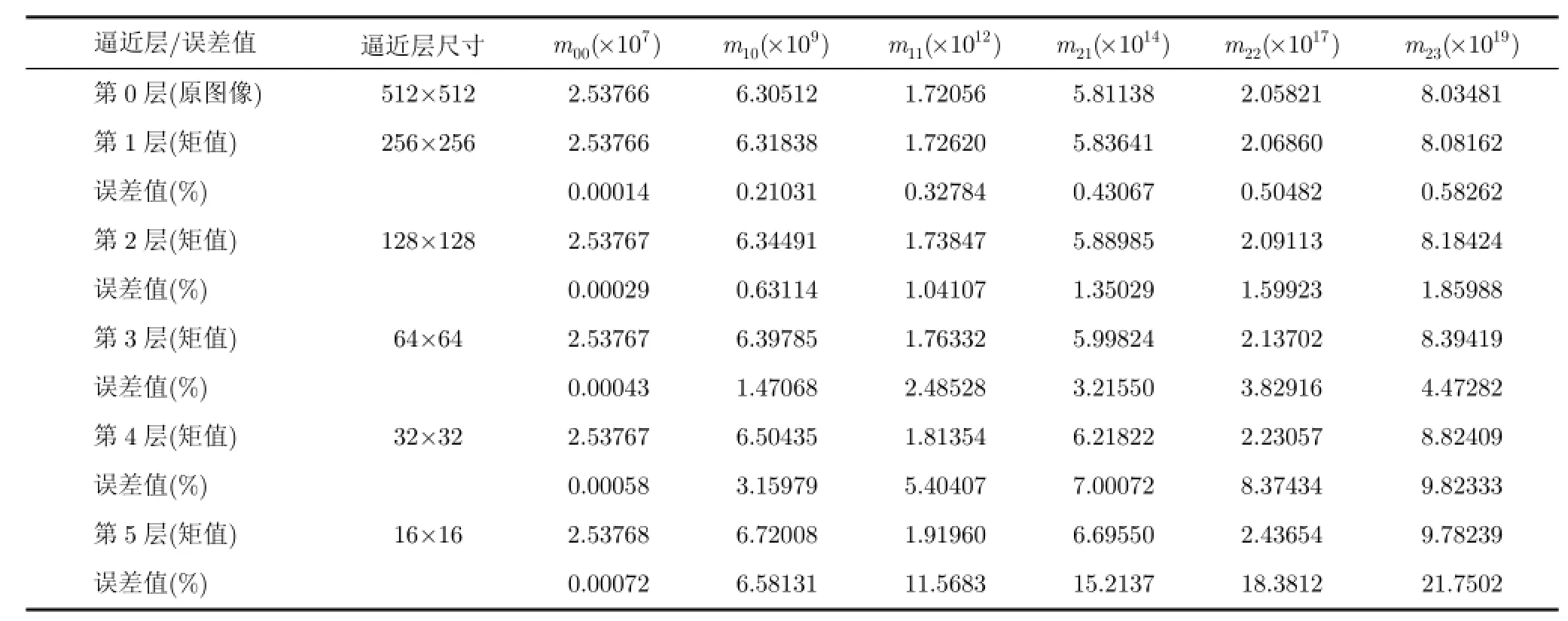
表1　基于分解近似系数的图像矩值及其误差值

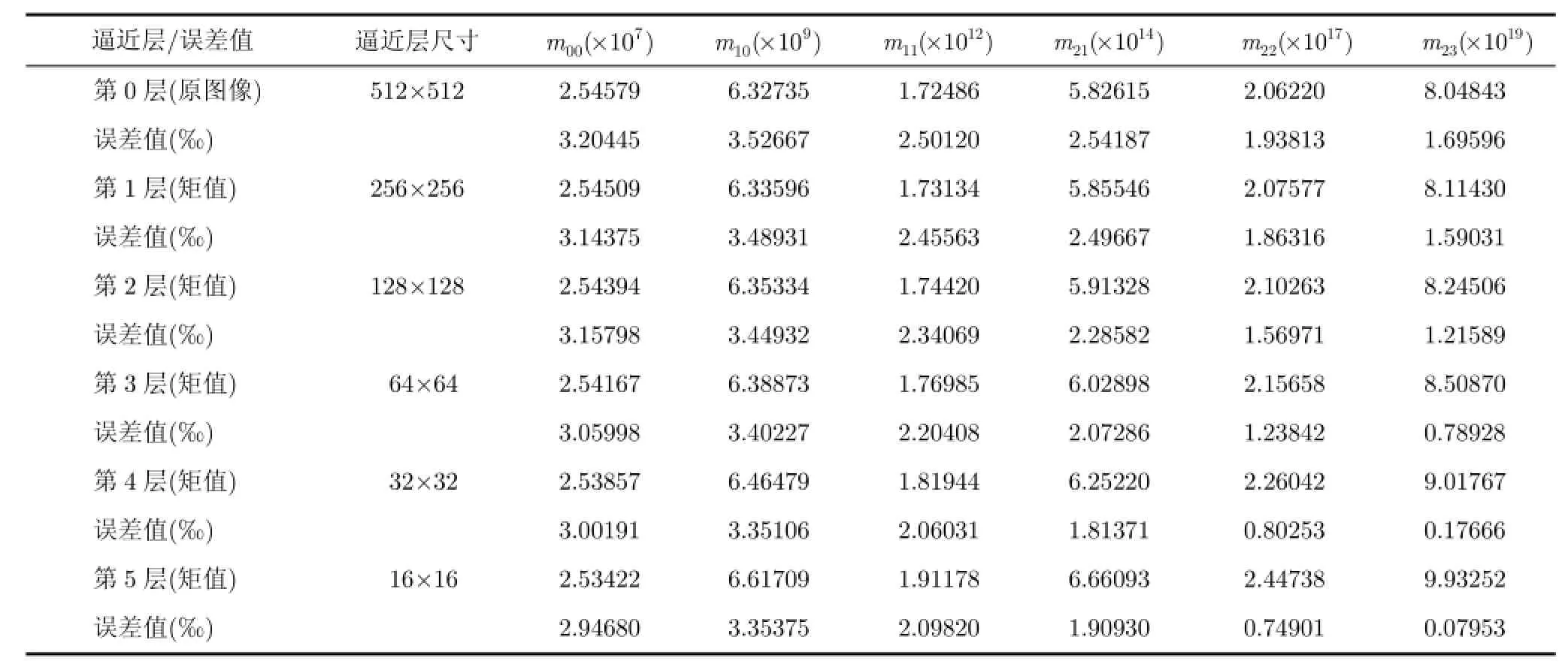
表2　基于分解近似系数的加噪图像矩值及其对比误差值

图1　原始Lena图像和加噪Lena图像

就式（14）的计算复杂度而言，由理论推导可知近似系数只有原始图像数据量的1/4。假设离散的原图像尺寸为N N×，一般几何矩是按式（11）对原始图像进行处理，其计算复杂度为而本文是对只有原始图像尺寸1/4的近似系数进行处理，原始数据量的减小显然将大幅降低计算量。假如式（14）的计算是基于第1层的近似系数，则其计算复杂度将降低为而如果其基于更大尺度（层数）的近似系数即尺度的近似系数，计算复杂度将进一步降为这显然在原始的计算复杂度基础上大幅减小了（4S-1）/4S的计算量。

5　结束语

本文从理论上推导得到了基于矩的小波矩不变量（小波不变矩），并指出它在实际应用中的局限性和需要注意的地方。多尺度分析是通过减少信号不必要的细节在大尺度范围内进行识别，而不变矩方法则要求尽可能多地保留物体的特征，特别是有助于区分近似物体的细节特征，这两种方法之间有一种内在的矛盾性和互补性。通常在模式识别中，需从总体轮廓上把握物体的特征，这样的识别方法具有抗噪性和抗干扰性［19］，而保留物体的细节特征有助于区分形近的物体但却导致对噪声和干扰的敏感。于是为了消除细节减少数据量，必须增大尺度，但这样做同时会使不变量数值不精确和导致表征细节特征信息不充分；另一方面，为尽可能准确地计算不变量必须尽量保持数据，从而要求逼近尺度不能太大。实际应用中两种方法的有机结合是很必要的，最合理的妥协就是每个物体在其合适的层次得到识别。

［1］李骏扬，金立左，费树岷，等.基于多尺度特征表示的城市道路检测［J］.电子与信息学报，2014，36（11）:2578-2585.doi: 10.3724/SP.J.1146.2014.00271.

LI Junyang，JIN Lizuo，FEI Shum in，et al.Urban road detection based on multi-scale feature representation［J］. Journal of Electronics&Information Technology，2014，36（11）:2578-2585.doi:10.3724/SP.J.1146.2014.00271.

［2］MALLAT S G.A Theory for multi-resolution signal decom position:the wavelet representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，1（7）:674-693.

［3］MALLAT SG.Multiresolution approximations and wavelet orthonormal bases of L2（R）［J］.Transactions of the American Mathematical Society，1989，315（1）:69-87.

［4］DAUBECHIES I.Orthonormalbasesof com pactly supported wavelets［J］.Communications on Pure And Applied Mathematics，1988，41（7）:909-996.

［5］PRASHAN P and MALIN P.Imagematching usingmoment invariants［J］.Neurocomputing，2014，137:65-70.doi: 10.1016/j.neucom.2013.02.058.

［6］HU M K.Visualpattern recognition by moment invariants［J］. IEEE Transactions on Information Theory，1962，8（2）: 179-182.

［7］谢生龙，王夏黎，董春雨，等.基于不变矩理论线矩法图像特征的提取［J］.计算机技术与发展，2014，24（11）:139-143.doi: 10.3969/j.issn.1673-629X.2014.11.035.

XIE Shenglong，WANG Xiali，DONG Chunyu，et al. Extraction of figure featuresbased on linemomentmethod of moment invariant theory［J］.Computer Technology and Developm ent，2014，24（11）:139-143.doi:10.3969/j.issn.1673-629X.2014.11.035.

［8］轩建平，郑锋.基于Coiflet的二维小波有限元构造与应用［J］.华中科技大学学报（自然科学版），2014，42（5）:21-24.doi: 10.13245/j.hust.140505.

XUAN Jianping and ZHENG Feng.Construction and application of two-dimentional wavelet finite element based on Coiflet［J］.Huazhong University of Science&Technology，2014，42（5）:21-24.doi:10.13245/j.hust.140505.

［9］HUR Y，PARK H，and ZHENG Fang.M ulti-D wavelet filter bank design using quillen-suslin theorem for laurent polynom ials［J］.IEEE Transactions on Signal Processing，2014，62（20）:5348-5358.doi:10.1109/TSP.2014.2347263.

［10］HUAE Y.Construction of com pactly supported nonseparable orthogonal wavelet w ith dilation 4［J］.Advanced M aterials Research，2014，1061（1）:1064-1069.

［11］金琪，戴汝为.基于矩表示的小波不变量［J］.模式识别与人工智能，1995，8（3）:179-187.

JIN Qiand DAIRuwei.Wavelet invariants based onmoment presentation［J］.Pattern Recognition and Artificial Intelligence，1995，8（3）:179-187.

［12］AYACHE A.Som e m ethods for constructing non-separable，orthonormal，com pactly supported wavelet bases［J］.Letter to the Editor In Applied And ComputationalHarmonic Analysis，2001，10（1）:99-111.

［13］DAUBECHIES I.Ten Lectures on Wavelets［M］.Vermont: Capital City Press，1992:299-300.

［14］徐应祥，关履泰.具有消失矩的新二元正交小波［J］.云南大学学报（自然科学版），2010，32（4）:385-391.

XU Yingxiang and GUAN Lütai.New bivariate orthogonal wavelets w ith vanishing moments［J］.Journal of Yunnan University，2010，32（4）:385-391.

［15］WONG Y R.Scene m atching w ith invariant m om ents［J］. Computer Graphics and Image Processing，1978，8（1）:16-24.

［16］潘泉，程咏梅，杜亚娟，等.离散不变矩算法及其在目标识别中的应用［J］.电子与信息学报，2001，23（1）:30-36.

PAN Quan，CHENG Yongmei，DU Yajuan，et al.Discrete moment invariant algorithm and its application on target recognition［J］.Journal of Electronics&Information Technology，2001，23（1）:30-36.

［17］沈会良，李志能.基于矩和小波变换的数字、字母字符识别研究［J］.中国图象图形学报，2000，5A（3）:249-252.doi:10.3969 /j.issn.1006-8961.2000.03.015.

SHEN Huiliang and LIZhineng.A study ofnumber and letter character recognition based on m om ents and wavelet transform［J］.Journal of Image and Graphics，2000，5A（3）: 249-252.doi:10.3969/j.issn.1006-8961.2000.03.015.

［18］毛贤光，李云欣，李罕，等.基于不变矩和小波分析的指横纹匹配新算法［J］.计算机工程与应用，2015，51（20）:172-177. doi:10.3778/j.issn.1002-8331.1310-0109.

MAO X ianguang，LI Yunxin，LI Han，et al.New m atching algorithm of knuck leprint based on m om en t invariants and wavelet mu lti-resolution analysis［J］.Computer Engineering and Applications，2015，51（20）:172-177.doi:10.3778/j.issn. 1002-8331.1310-0109.

［19］丁晓青.汉字识别研究的回顾［J］.电子学报，2002，9（9）: 1364-1368.doi:10.3321/j.issn:0372-2112.2002.09.029.

DING Xiaoqing.Chinese character recognition:a review［J］. Acta Electronica Sinica，2002，9（9）:1364-1368.doi:10.3321/ j.issn:0372-2112.2002.09.029.

刘斌：男，1963年生，教授，博士生导师，主要从事模式识别、图像处理及小波理论的研究.

高强：男，1988年生，硕士生，研究方向为图像处理、模式识别.

Moment Invariants Based on Two Dimensional Non-separable Wavelet Transform

LIU Bin GAO Qiang
（School ofComputer and Information Engineering，Hubei University，Wuhan 430062，China）

Searching for wavelet invariants is a key issue in m ultiresolu tion analysis.On the other hand，them ethod ofmoment invariants is fully developed both in the theory and the p ractice.A kind ofwaveletmoment invariants are given based on the image invariantmoments and wavelet app r-oximation coefficients from the lim ited number of scales of the image.A fairy com plete result on theory and experiment is obtained.At the same time，some problem sof the theory and method are pointed out in the p racticalapplication.Finally，the application relationship betweenmu lti-scale analysis and invariantmoment is briefly described.

Pattern recognition；M ulti-scale analysis；Two dim ensional non-separable wavelet；Invariantm om ent；Smoothness；App roximation coefficients

s:The National Natural Science Foundation of China（61471160），The Key P roject of the Natural Science of Hubei Province（2012FFA 053）

TP391.41

A

1009-5896（2016）08-2085-06

10.11999/JEIT 151218

2015-11-03；改回日期：2016-05-03；网络出版：2016-06-12

高强shengqiang8814@qq.com

国家自然科学基金（61471160），湖北省自然科学基金（2012FFA 053）