具有二维状态转移结构的随机逻辑及其在神经网络中的应用

季　渊　陈文栋　冉　峰　张金艺David LILJA（上海大学微电子研究与开发中心上海200072）（上海大学机电工程与自动化学院上海200072）（明尼苏达大学电子与计算机工程系明尼阿波利斯55455）



具有二维状态转移结构的随机逻辑及其在神经网络中的应用

季渊*①②陈文栋①冉峰①②张金艺①David LILJA③①
①（上海大学微电子研究与开发中心上海200072）
②（上海大学机电工程与自动化学院上海200072）
③（明尼苏达大学电子与计算机工程系明尼阿波利斯55455）

随机计算是一种特殊的基于概率数据码流的数学计算方法，其优点在于可以采用非常简单的数字逻辑完成复杂数学运算，从而大幅降低硬件实现成本。该文首先讨论了随机计算的基本原理和主要运算逻辑，论述了传统线性状态机的不足，并分析了一种2维状态转移拓扑结构，推导了通过2维有限状态机实现高斯函数的方法。在此基础上，提出一种随机径向基函数神经网络模型，其硬件实现成本非常低，而性能与传统神经网络相当。两类模式识别实验结果显示，所提出的随机径向基函数神经网络的输出值均方误差与相应结构传统神经网络的差别小于1.3%。FPGA实验结果显示，数据宽度为12位时，随机中间神经元的电路面积仅为传统插值查表结构的1.2%、坐标旋转数字计算方法（CORDIC）的2%。通过改变输入码流长度，该神经网络可以在处理速度、功耗和准确性之间作出平衡，具有应用灵活性，适用于对成本、功耗要求较高的应用如嵌入式、便携式、穿戴式设备。

随机计算；人工神经网络；径向基函数；模式识别

正是由于这些特点，随机计算非常适合于并行计算［6］、容错计算［7］、可靠性计算［8］以及一些对数据精度要求并不十分严格的运算密集型应用，例如通信随机编码［9］、图像处理［10］，尤其是人工神经网络［11］。由于神经网络包含大量乘法、加法和指数运算，消耗大量逻辑运算资源，因此用传统方法进行硬件实现的成本较高［12，13］，而基于随机计算的神经网络（也称为随机神经网络）由于运算逻辑简单，更容易组成大规模网络结构。文献［5］提出了比例缩减加法器、线性有限状态机、随机除法器等随机计算逻辑单元，改进了随机神经网络的性能，并将这些改进型随机逻辑单元用于一种基于软竞争学习算法的神经网络中进行字符识别应用［14］。然而，这种随机神经网络仍采用了单一的sigm oid激活函数，网络类型和网络性能都受到一定限制。

近年来，文献［15］提出了一种基于马尔可夫链（Markov chain）的2维有限状态机（FSM）拓扑结构，本文在此基础上，推导了利用2维有限状态机来实现高斯函数的具体过程，并根据码流的全相关性，利用一个简单的XNOR门实现了减法运算，然后讨论了将随机逻辑应用于径向基函数（Radial Basis Function，RBF）神经网络的方法［16］，得到随机径向基函数神经网络，将该网络应用于两类模式识别实验（鸢尾花识别和光学字符识别），最后在FPGA上得到验证。

2　随机逻辑运算单元

2.1数值定义

随机计算中，传统的确定性数据都转化为概率数据。设X（t）为一个长度为L的比特码流（L为正整数），t=0，1，2，…，L，X（t）∈［0，1］，将X（t）简记为X，令x表示X中出现数字1的概率，即x=P（X=1），例如，码流X=0010011001010001对应的x为0.375。随机计算可采用两种数据格式：无符号数（Unipolar）和有符号数（Bipolar），分别用yu和ys表示，其取值大小和范围由式（1）和式（2）给出：

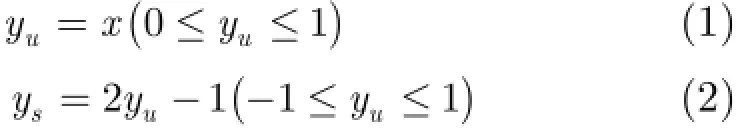
根据式（1）和式（2）可以得到，码流X作为无符号数和有符号数时分别表示0.375和-0.25（即yu=0.375，ys=-0.25）。这两种数据表示方式本质上相同，可以同时出现在同一个系统中。确定性数可通过比较器和随机数发器转换为随机码流，随机码流可通过二进制计数器转换为确定性数［5］。

2.2传统随机逻辑运算单元

2.2.1乘法假定随机码流A和B均为伯努利（Bernoulli）序列［17］，用P（X）表示码流X中所含有数字1的概率，若采用无符号数据格式，则码流A和B之间的乘法可以用一个逻辑与门（AND）来实现，若采用有符号数据格式，则A和B之间的乘法可以用一个异或非门（XNOR）来实现［5］。

2.2.2加法早期加法用或门（OR）实现，但存在误差［1］。文献［5］提出一种比例缩放加法器，利用多路选择器（MUX）实现加法，但是比例缩放加法器每经过一次运算，输出值精度减半，因此仍然存在一定误差。本文在实现径向基函数时，将加法运算转化为乘法运算，从而避免了精度损失问题，第3节将详述。

2.2.3线性状态机神经网络的激活函数一般为sigm oid函数。早期的随机神经网络采用二进制计数器、查找表、组合逻辑或者预定义码流来实现激活函数，但是性能都不太理想。文献［5］提出一种线性状态转移结构如图1所示，通过改变参数P和Q可以实现多种sigm oid函数。然而，当利用该线性状态机实现指数函数时，状态数N往往大于64，需要较多硬件资源，且在零点的近似效果不理想，无法保证指数函数在零点对称。

2.3增强型随机逻辑运算单元

2.3.1减法传统随机计算的输入序列必须保持不相关［1，5］。但是，如果使输入序列完全相关（例如，由相同的随机数源发生器产生），则经过二输入XNOR门后，逻辑结果不再是乘法：当输入序列相应位的值不同时，输出值为0，当输入序列相应位的值相同时，输出值为1，这样，输出码流中0的数量代表A和B中不相同的位数，1的数量代表A和B中相同的位数，因此，两个输入码流中数据不同的概率被检测出来，从而实现了减法。XNOR门输入为两个无符号数码流，输出为这两个码流减法的绝对值（无符号数）。用XOR实现减法时，其输出为XNOR的逻辑取反。

图1　线性状态转移结构

2.3.2 2维状态机考虑图2所示的状态转移拓扑结构，状态总数为M×N（S0至1MN-S），状态根据输入值在2维空间内向相邻状态转移，输入变量由输入码流x和调制码流k组成，共有4种组合：00，01，10，11，该组合值决定了状态的跳转方向，例如11为向右跳转，00为向左跳转，当状态处于最右或最左的状态时，即使输入码流为向右或向左跳转时，当前状态也保持不变，形成饱和；输入码流组合为10和01的过程类似。该状态变化过程可以由齐次时间的Markov链描述，其特征为一个不可约的、非周期性的、遍历性的状态机［15］。根据Markov定理，当状态转移次数足够多时，该结构可等效为一个与初值状态无关的概率分布。若用PSt（t为当前状态编号，t=0，1，…，MN-1）来表示状态t出现的概率，用PX来表示输入随机码流x的概率值，用PK来表示调制码流k的概率值，则PSt为

图2　 2维状态转移结构

其中，i是水平方向上的状态编号，j是垂直方向上的状态编号，tx和ty为

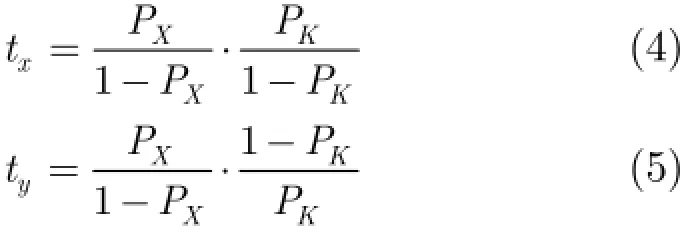
由式（3）得到的概率可用于模拟复杂目标函数。图3给出了一种求近似函数的硬件架构，x，k，qt和y都是数据位宽为1 bit的随机码流，采用无符号数据格式，其中，x和k为2维状态机（2D-FSM）的输入码流，qt是一组预先定义好的随机参数码流，其值由Pqt表示。信号cst表示2维状态机的当前状态，连接到多路选择器（MUX）的选择端。若cst为t（t=0，1，…，MN-1），则qt就被选择作为输出端y的输出值。因此，y的概率值（用PY表示）可以由cst和Pqt来调制［16］。

图3　用随机计算实现复杂函数的逻辑电路结构

若设目标函数为T（PX），则可定义目标误差为

由于PY可以表示为PX，PK和Pqt的函数，因此通过求解二次函数ε的最小值，就可以得到调制码流k和qt的概率值。表1列出了3种高斯函数作为目标函数的求解结果。由于高斯函数为对称函数，因此PK均为0.5。Pqt通过MATLAB求得，其值关于中心点对称。PY1和PY2的表达式相同，但是状态数不相同，它们都关于直线x=0.5对称，逼近结果如图4所示。可以发现，在目标函数相同的情况下，8状态和16状态的结构都较好逼近目标函数。与线性状态转移结构比较［5］，在实现相同函数时，2维状态转移结构使用的状态数量大幅减少，输出曲线更光滑，且2维状态转移结构可以实现更多复杂函数。图5显示了PY3的逼近效果，码流长度为1 kbit的输出误差较大，码流长度为10 kbit的输出误差大幅减少，说明输出函数的误差与随机码流的长度有关。图4和图5的结果表明，可以用一种简单的2维状态机来实现高斯函数。

3　随机神经网络模型

3.1径向基函数神经网络分解

本文以一个3层径向基函数网络为例。网络输入层包含了输入对象的原始特征，这些特征用矢量xi来表示（i=1，2，…，I，I为输入神经元个数）。中间层包含了径向基函数对输入神经元提取的抽象特征，用矢量yj来表示（j=1，2，…，J，J为中间神经元个数），采用高斯函数作为径向基函数，即

其中，cij为高斯函数的中心点，σ2控制了高斯函数的弯曲程度。矢量zk为输出神经元（k=1，2，…，K，K

为输出神经元个数），其值是中间神经元的线性组合，即

其中，wjk是权值矩阵，bk是线性偏置。cij，σ，qt，wjk和bk的值在网络训练过程中确定。然而，式（7）表示的径向基函数并不容易直接用硬件实现，因此，把该范数展开得到：

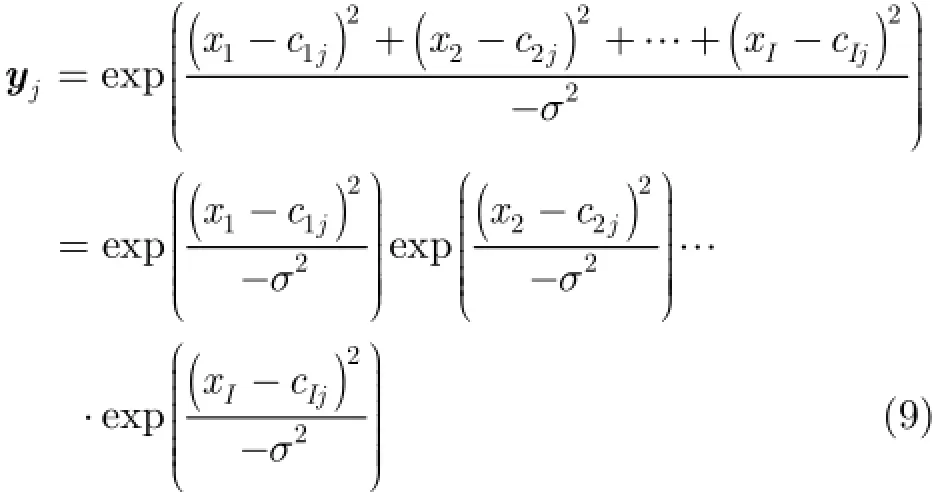
可见，yj的计算包含3个计算过程：（1）输入神经元xi和高斯函数中心点cij的差值；（2）中心点为零的高斯函数；（3）各高斯函数间的乘积。

3.2随机径向基函数神经网络

根据式（9）构造一个由随机逻辑实现的径向基函数神经网络（以下简称随机RBF网络），其输入神经元将输入的确定性二进制数di转换为随机码流xi，中间神经元和输出神经元的结构如图6所示，网络参数cij，k，qt，wjk和bk存储于外部存储器中，通过移位寄存器输入网络。

表1　 2维状态转移结构近似目标函数中的参数

图4　用2维状态机综合的高斯函数PY1和PY2

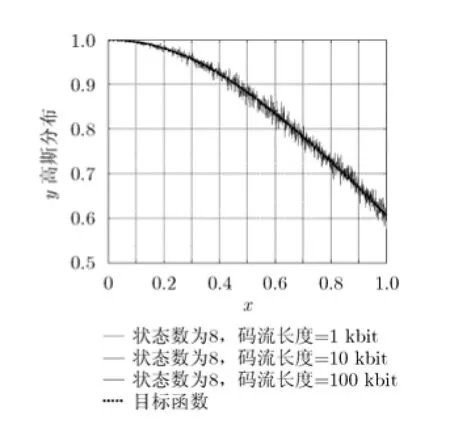
图5　用2维状态机综合的高斯函数PY3

对于中间神经元，高斯函数的中心点cij被转换为随机码流，其所使用的随机源与输入神经元使用的随机源相同，以保证xi和cij完全相关，从而使用XNOR门将随机码流xi和高斯函数中心点cij相减（如2.3.1节所述），所得I个差值的绝对值经过I个2维状态机（如图3所示）完成高斯函数计算，其中，调制码流k和qt由独立的随机数发生器产生，以保证所得高斯函数的输出值Ti（PX）各不相关，从而可以使用一个AND门将该中间神经元中所有高斯函数的输出值相乘，得到中间神经元的输出yj。

输出神经元可由两种方式实现，一种是采用随机逻辑，另一种是采用传统的确定性逻辑。对于传统的确定性逻辑，可以先将中间神经元输出的随机码流yj转换为确定性二进制数，然后采用一组乘法器和加法器进行式（8）的线性迭代运算，得到输出神经元的值zk，每个输出神经元的结构相同，但权值wjk和偏置值bk不同。对于随机逻辑，由于输出神经元的权值wjk和偏置bk可能大于1，因此先要将wjk和bk进行等比例缩小，使其取值范围为［-1，1］，然后使用XNOR门完成yj和wjk有符号乘法计算，最后将结果乘以原来的缩小系数，形成J路随机码流zik。为了避免随机加法运算，该网络先将J路随机码流zik转换为确定性二进制数，利用确定数的二进制加法器将转换结果相加，得到输出神经元的输出结果zk，从而提高了精度。

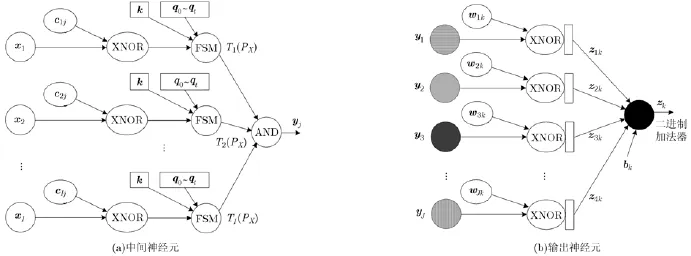
图6　随机径向基函数神经网络的神经元结构

4　实验与结果讨论

4.1鸢尾花识别实验

鸢尾花数据组包含3种类型鸢尾花，每种花各有50组样本，每组样本均含有4种数据：萼片、花瓣的长度和宽度。为了识别花的类型，首先构建一个确定性数RBF网络，该网络包含4个输入神经元、8个中间神经元和3个输出神经元，随机抽取75个样本作为训练集，剩余75个样本作为测试集，采用正交最小二乘法训练，得到测试样本识别率为97.33%。然后构建两个同样结构（4×8×3）的随机RBF神经网络M 1和M 2，M 1的中间神经元采用图6（a）的随机逻辑、输出神经元采用确定逻辑，M 2的所有神经元均采用图6的随机逻辑。M 1和M 2中间神经元2维状态机的状态数均为8。对M 1和M 2分别进行鸢尾花种类识别测试，每个测试项重复2000次以减少随机数波动影响，测试结果如图7所示。MSE用于衡量随机网络与确定网络的偏离程度。在M 1中，当测试码流为10 kbit时，平均识别率为93.4%；当测试码流为500 kbit时，平均识别率达到96.7%。在M 2中，当测试码流为1Mbit时，MSE为0.051，比相同情况M 1的MSE高20%，这是因为M 2的输出神经元采用了随机加法器。该误差可以通过增大随机码流长度得到改善，这一事实也证明了随机码流可以动态调整运算速度和精度。

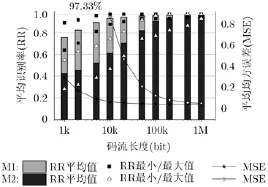
图7　随机径向基函数网络M 1和M 2对鸢尾花的识别率（柱体）和MSE（实线）

图8　 E-13B M ICR字体中注入数据噪声

4.2光学字符识别实验

采用E-13B M ICR字体作为识别对象。在标准M ICR字体中加入两种随机数据噪声：像素模糊和像素错误，分别用BR（Blur Rate）和ER（Error Rate）表征，前者指像素灰度的改变程度，后者指像素灰度值完全错误的比例，如图8所示。每个字符均采用7×8像素阵列描述，像素灰度值经过标准化后输入至随机径向基函数神经网络，网络拥有56个输入神经元、15个中间神经元和14个输出神经元，每一个输出神经元都代表了M ICR字体识别结果。网络采用正交最小二乘法训练后得到参数cij，k，qt，wjk和bk。实验采用网络结构M 3和M 4，其中，M 3的中间神经元采用随机逻辑、输出神经元采用确定性逻辑，M 4的中间神经元和输出神经元均采用随机逻辑。采用MATLAB对M 3建模和仿真，识别注入随机数据噪声的M ICR字体。图9示意了不同码流长度的识别结果。对于网络M 3，当码流长度从1 kbit增加到100 kbit时，字体识别率有2%～3%的改善，MSE有5%～8%的改善，字体识别率和MSE最终向确定性网络（DN）的结果收敛。对于网络M 4，当ER为10%，且码流长度大于40 kbit时，字体识别率几乎为100%；当ER为20%，码流长度从40 kbit增加到1Mbit时，字符识别率从91%增加到96.7%，最终收敛于相应的确定性网络。

图9　随机径向基函数网络和对应确定性网络的M ICR字体识别率（实线）和MSE（虚线）（DN：确定性神经网络）

上述数据为2000次实验结果的平均值。图10记录了100次MSE实验结果。对于M 3，码流长度1 kbit时的MSE与相应确定性网络的MSE差别为3.26%，码流长度10 kbit时的差别为1.3%；对于M 4，码流长度为100 kbit时差别为7.61%，码流长度为1 Mbit时的差别为2.17%。这些MSE差别均小于文献［5］所提出的软竞争学习神经网络的字符识别实验［14］，在文献［5］实验中，确定性网络和随机网络的MSE差别在第1层软件竞争学习网络中为31%（0.545 vs0.715），在第2层线性网络中为10%（4.77 vs 5.26）。

4.3硬件实现比较

采用A ltera Cyclone IIIFPGA（EP3C80F780C8）对网络结构M 1～M 4进行硬件实现，该FPGA共有81264个逻辑单元LE和430个管脚，综合结果如表2所示。网络参数（cij，k，qt，wjk和bk）存储于外部存储器中，通过移位寄存器移入网络。对于M 1和M 3，中间神经元采用随机逻辑实现，输出神经元采用二进制加法器和乘法器实现，对于M 2和M 4，中间神经元和输出神经元均采用随机逻辑实现。当数据位宽增加时，两个网络结构的总规模都呈现增长趋势，但是中间神经元的规模保持不变，说明基于随机逻辑的中间神经元规模与数据位宽无关。M 2，M 4的输出神经元规模分别大于M 1，M 3，随着数据位宽增加，其占系统总资源的比例不断扩大，说明与传统的确定性逻辑相比，随机逻辑的硬件资源优势随着网络规模的增大变得越来越明显。

图10　 MSE的随机波动（BR=10%，ER=30%），SL：码流长度（Stream length）

4.4综合性能比较

表3列出了给定FPGA的前提下，不同RBF网络实现方式的硬件资源和性能比较。A为电路面积，以摊销至每一个网络输入所需要的中间神经元LE数量作为电路面积资源的衡量单位（电路面积除以输入神经元总数再除以中间神经元总数）；C为时钟，以每完成一次识别操作所需要的时钟数作为网络性能的衡量单位；O为操作次数，以每秒能够完成的最大操作次数作为网络性能的衡量单位。从表中可见，随机RBF网络的LE摊销值为22个，远小于其他3种方法。全查找表结构虽然只需要一个时钟周期来完成操作，但是所需要的查找表过于庞大。插值查找方式减少了查找表规模，但是增加了计算时间。CORDIC（坐标旋转数字计算）算法是一种流行的指数函数计算方法，它只需要二进制加法器，比查找表规模更小。这几种算法的性能通过R0，R1，R2 3种指标衡量，其中，R0为面积A和时钟C的乘积的倒数（R0=1/（AC）），代表面积和性能的综合指标；R 1为面积A的平方和时钟C的乘积的倒数（R 1= 1/（A2C）），代表以面积为优先的衡量指标；R2为操作次数O除以面积A（R2=（O/A）），代表单位面积可以达到的操作性能。其比较结果如图11所示，纵坐标为归一化后的计分值。总体看来，10位随机网络结构拥有最好的R0，R1和R2指标，但是精度偏低。在同样12位的数据宽度情况下，若以R1为考查指标（即强调面积优先），则随机网络拥有最高分值，若以R2为考查指标时（即强调单位面积性能），则随机网络与CORDIC拥有较高的分值。若提高数据宽度至14位，则随机网络在面积上仍有优势。综上所述，随机网络的性能和传统电路相差并不明显，但是拥有非常大的电路面积优势。

表2　随机径向基函数神经网络的FPGA实现资源，单位：LE（逻辑单元），网络规模：56×15×14

表3　不同实现方式的径向基函数神经网络的硬件资源和性能比较

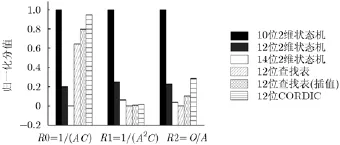
图11　不同网络实现方式的性能比较

随机计算给神经网络提供了一种并行解决方案。由于神经网络包含大量乘法、加法、指数运算，传统基于指令运算的微处理器需要非常多的时钟周期，对于本实验M 3和M 4的56×15×14网络结构，若每个节点都进行一次乘法和加法，则至少需要56×15×14×2=23520个计算时钟，再加上指数运算、控制指令、读写数据则需要更多时钟周期，而随机RBF网络仅需要10k个时钟就可以得到基本正确的结果，硬件开销远小于传统微处理器，因此随机计算的综合性能相对传统的微处理器的串行指令运行方式有较大优势。

5　结束语

计算机的处理能力正受到越来越严重的瓶颈限制。本文提出了一种思路，可以运用非常精简的随机运算逻辑来实现大规模神经网络。实验证明，本文所提出随机径向基函数神经网络的中间神经元的电路面积只有传统插值查表结构神经元的1.2%，CORDIC法的2%，而其运算精度非常接近于传统网络，且其MSE波动范围非常小。从实验结果可以推论，这些随机逻辑可以应用于更为复杂的网络结构中。当硬件成本为主要考虑因素时，随机网络具有很大优势，尤其适应于对成本、功耗要求较高而对于精度要求并不高的应用如嵌入式、移动式、穿戴式设备。另一方面，随机网络的性能随着随机码流长度而改变，因此，在相同的网络结构下，可以通过改变码流长度来产成不同的计算精度，这给设计者带来了灵活性，可以在不改变硬件结构的情况下对网络性能、电路功耗和运算速度3个因素进行动态平衡。最后，由于随机计算是基于概率数的运算，网络可以容许输入数据的误差和电路错误，当电路中有个别数据发生改变时，其最终结果并不会发生根本变化，该特点将是今后的研究方向之一。

［1］GAINES B R.Stochastic Com puting System s（Chapters）in Advances in Information System s Science［M］.New York: Plenum，1969:37-172.

［2］HAYES J P.Introduction to stochastic com puting and its challenges［C］.2015 52nd ACM/EDAC/IEEE Design Automation Conference（DAC），San Francisco，CA，USA，2015:1-3.doi:10.1145/2744769.2747932.

［3］ALAGHI A and HAYES J P.Survey of stochastic computing［J］.ACM Transactions on Embedded Computing System s，2013，12（2s）:1-19.doi:10.1145/2465787.2465794.

［4］MOONS B and VERHELST M.Energy-efficiency and accuracy of stochastic com puting circuits in emerging technologies［J］.IEEE Journal on Em erging and Selected Topics in Circuits and Systems，2014，4（4）:475-486.doi: 10.1109/JETCAS.2014.2361070.

［5］BROWN B D and CARD H C.Stochastic neural computation.I.Com putational elem ents［J］.IEEE Transactions on Computers，2001，50（9）:891-905.doi: 10.1109/12.954505.

［6］QIANWeikang，LIXin，RIEDELM D，et al.An architecture for fault-tolerant com putation w ith stochastic logic［J］.IEEE Transactions on Computers，2011，60（1）:93-105.doi: 10.1109/TC.2010.202.

［7］HAN Jie，CHEN Hao，LIANG Jinghang，et al.A stochastic computational app roach for accurate and efficient reliability evaluation［J］.IEEE Transactions on Computers，2014，63（6）: 1336-1350.doi:10.1109/TC.2012.276.

［8］ALAWAD M and LIN M ingjie.FIR filter based on stochastic com puting w ith reconfigurable d igital fabric［C］.2015 IEEE 23rd Annual International Sym posium on Field-Programmable Custom Computing Machines（FCCM），Vancouver，BC，Canada，2015:92-95.doi:10.1109/FCCM. 2015.32.

［9］TEHRANI S S，NADERI A，KAMENDJE G A，et al. M ajority-based tracking forecast M em ories for Stochastic LDPC Decoding［J］.IEEE Transactions on Signal Processing，2010，58（9）:4883-4896.doi:10.1109/TSP.2010.2051434.

［10］LIPeng，LILJA D J，QIAN W eikang，et al.Com pu tation on stochastic bit stream s digital image processing case studies［J］. IEEE Transactions on Very Large Scale Integration（VLSI）System s，2014，22（3）:449-462.doi:10.1109/TVLSI.2013. 2247429.

［11］ZHANG Da and LIHui.A stochastic-based FPGA controller for an induction motor drivew ith integrated neural network algorithm s［J］.IEEE Transactions on Industrial Electronics， 2008，55（2）:551-561.doi:10.1109/TIE.2007.911946.

［12］王守觉，李兆洲，陈向东，等.通用神经网络硬件中神经元基本数学模型的讨论［J］.电子学报，2001，29（5）:576-580.

WANG Shou jue，LI Zhaozhou，CHEN X iangdong，et al. Discussion on the basic mathematicalmodels of neurons in general purpose neurocom puter［J］.Acta Electronica Sinica，2001，29（5）:576-580.

［13］吴大鹏，赵莹，熊余，等.基于小波神经网络的告警信息相关性挖掘策略［J］.电子与信息学报，2014，36（10）:2379-2384. doi:10.3724/SP.J.1146.2013.01701.

WU Dapeng，ZHAO Ying，XIONG Yu，et al.A larm information relevance m ining mechanism based on wavelet neural network［J］.Journal of Electronics&Information Technology，2014，36（10）:2379-2384.doi:10.3724/SP.J.1146. 2013.01701.

［14］BROWN B D and CARD H C.Stochastic neural computation.II.Soft com petitive learning［J］.IEEE Transactions on Computers，2001，50（9）:906-920.doi: 10.1109/12.954506.

［15］LI Peng，LILJA D J，QIAN W K，et al.The synthesis of com p lex arithm etic com putation on stochastic bit stream s using sequential logic［C］.2012 IEEE/ACM International Conference on Com puter-Aided Design（ICCAD），San Jose，CA，USA，2012:480-487.doi:10.1145/2429384.2429483.

［16］JI Yuan，RAN Feng，MA Cong，et al.A hardware im plementation of a radial basis function neural network using stochastic logic［C］.2015 Design，Automation&Test in Europe Conference&Exhibition（DATE），G renoble，France，2015:880-883.

［17］马承光，仲顺安，LILJA D J，等.基于超几何分解的随机运算系统分析方法［J］.电子与信息学报，2013，35（2）:355-360.doi: 10.3724/SP.J.1146.2012.00711.

MA Chengguang，ZHONG Shunan，LILJA D J，et al. Analysis m ethod of stochastic com puting system based on hypergeometric decom position［J］.Journal of Electronics& Information Technology，2013，35（2）:355-360.doi:10.3724/ SP.J.1146.2012.00711.

季渊：男，1980年生，副研究员，研究方向为大规模集成电路设计、神经网络与机器学习、硅基微显示器.

陈文栋：男，1993年生，硕士生，研究方向为神经网络与机器学习.

冉峰：男，1954年生，教授，研究方向为大规模集成电路设计、微电子技术、半导体器件.

David LILJA：男，教授，研究方向为计算机架构、并行计算、高性能计算.

Stochastic Logics with Two-dimensional State Transfer Structure and Its App lication in the A rtificial Neural Network

JIYuan①②CHEN Wendong①RAN Feng①②ZHANG Jinyi①David LILJA③①
①（M icroelectronic Research and Developm ent Center，Shanghai University，Shanghai 200072，China）
②（School ofM echatronic Engineering and Automation，Shanghai University，Shanghai 200072，China）
③（Departm ent ofElectrical and Computer Engineering，University ofMinnesota，M inneapolis 55455，USA）

Stochastic com puting is a special algorithm that perform smathematical operations with probabilistic values of bit stream s rather than traditional determ inistic values.Themain advantage of stochastic computing is its great sim plicity of hardwarearithmetic units formathematical operations to reduce the circuit cost.This paper discusses the p rincip le of the stochastic computing and itsmain arithmetic logic.It analyzes a two-dimension state transition topology structure，and discusses the Gaussian function im p lem entation m ethod based on the two-d im ension Finite State M achin（FSM）.Then，a low cost stochastic radial basis function neural network m odel is proposed.Results from two pattern recognition tests show that the d ifference of them ean squared error between the stochastic network output value and the corresponding determ inistic network output value can be less than 1.3%.FPGA im plementation results show that the hardware resource requirement of the p roposed stochastic hidden neuron is only 1.2%of the corresponding determ inistic hidden neuron w ith the interpolated look-up table，and is 2.0%of the CORDIC algorithm.The accuracy，speed and power of the stochastic network can be tradeoff dynam ically.This network is suitab le for the low cost and low power app lications like embedded，portable and wearab le devices.

Stochastic com puting；Artificial neural network；Radial Basis Function（RBF）；Pattern recognition

1　引言

随机计算（stochastic com puting）［14］-是一种特殊的基于非确定性数据的计算方法，最初由文献［1］提出，它以比特码流中出现1（或0）的概率作为运算数值，在概率域中进行数学运算。与传统的基于确定性数的计算方法（determ inistic computing）相比，随机计算的最大优势在于所需要的运算逻辑资源非常小，例如，两个数之间的乘法运算可以简单地用一个二输入与门来实现［5］。其次，由于随机计算采用概率数作为运算数据，其运算过程中的输入噪声或数据错误不会导致最终结果的完全偏离，因此，随机计算的抗干扰能力强于传统的确定性计算。第三，随机计算的运算精度与比特码流的长度相关，更长的码流可以产生更高的数据精度，这给系统设计带来了较好的灵活性，在同一个硬件系统中，可以根据应用场景特点采用不同的码流长度，实现运算速度、电路功耗和运算精度的动态调整。

The National Natural Science Foundation of China（61376028）

TP302.7

A

1009-5896（2016）08-2099-08

10.11999/JEIT 151233

2015-11-03；改回日期：2016-04-08；网络出版：2016-05-24

季渊jiyuan@shu.edu.cn

国家自然科学基金（61376028）