对称稳定分布噪声下基于广义相关熵的DOA估计新方法
2016-08-30邱天爽任福全李景春谭海峰大连理工大学电子信息与电气工程学部大连116024国家无线电监测中心北京100037北京邮电大学信息与通信工程学院北京100876
王 鹏 邱天爽* 任福全 李景春 谭海峰(大连理工大学电子信息与电气工程学部大连116024)(国家无线电监测中心北京100037)(北京邮电大学信息与通信工程学院北京100876)
对称稳定分布噪声下基于广义相关熵的DOA估计新方法
王鹏①邱天爽*①任福全①李景春②谭海峰②③①
①(大连理工大学电子信息与电气工程学部大连116024)
②(国家无线电监测中心北京100037)
③(北京邮电大学信息与通信工程学院北京100876)
针对稳定随机变量有限二阶矩不存在的特点,该文定义了一种新的广义相关熵,并从理论上证明了对称稳定分布随机变量广义相关熵的有界性。此外,提出了一种稳定分布噪声下基于最小广义相关熵准则的DOA估计新方法,给出了一种迭代优化算法并通过仿真实验分析了算法的收敛性。仿真结果表明,与现有基于分数低阶矩的FLOM-MUSIC、基于类相关熵的CRCO-MUSIC以及基于lp范数的ACO-MUSIC算法相比,所提方法可以获得更好的估计结果,尤其是在高脉冲性噪声环境下具有更加明显的优势。
波达方向估计;相关熵;广义相关熵;稳定分布噪声;MUSIC算法
1 引言
DOA(Direction O f Arrival)估计是阵列信号处理中的基本问题之一,广泛应用于雷达、声呐以及无线电通信等领域[1]。多重信号分类[2](MU ltiple SIgnal Classification,MUSIC)算法能够实现DOA的超分辨率估计,但是传统算法多假设背景噪声服从高斯分布。实际上,由于受到自然因素(如大气噪声、海杂波等)以及人为因素(如电动机等电磁设备)的影响,噪声可能呈现较强的脉冲性,此时利用A lpha稳定分布[3]进行描述更加合适。与高斯分布随机变量不同,A lpha稳定分布随机变量不具有有限二阶矩,传统MUSIC方法不再适用。
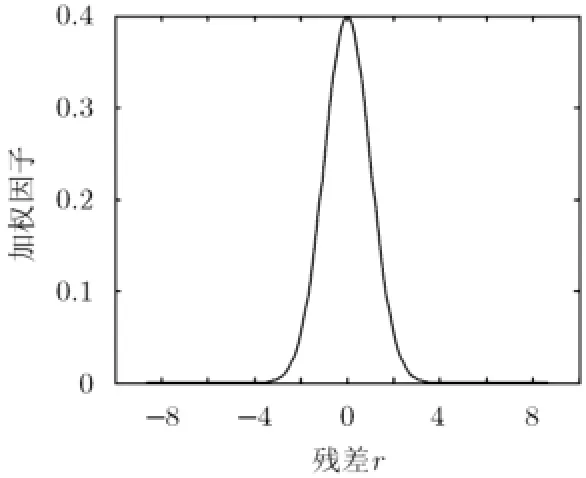
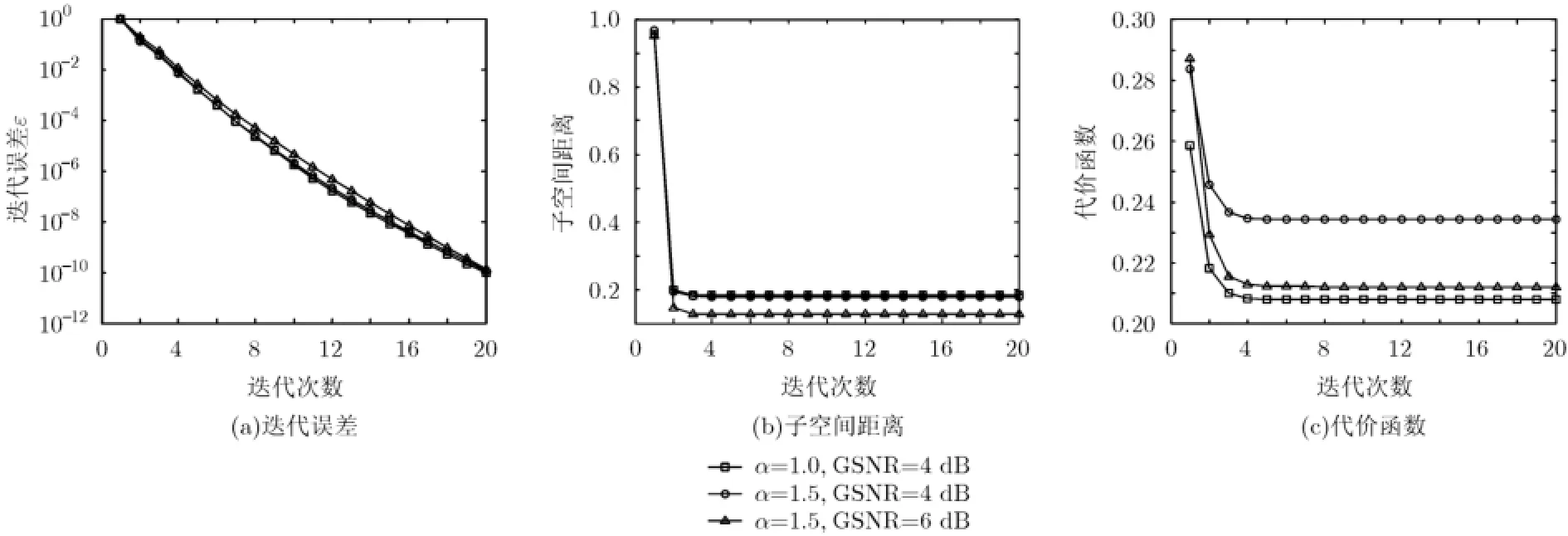
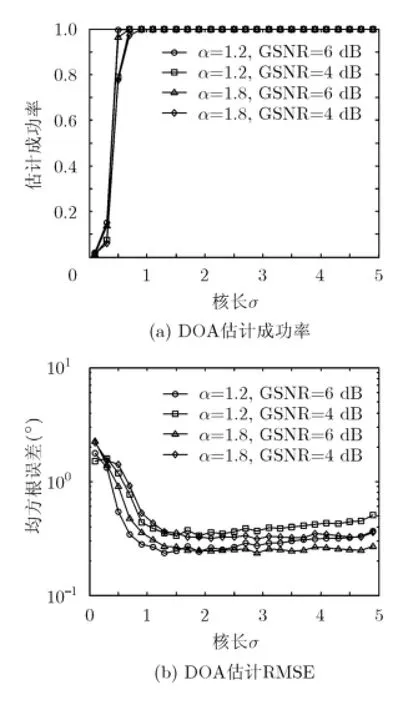
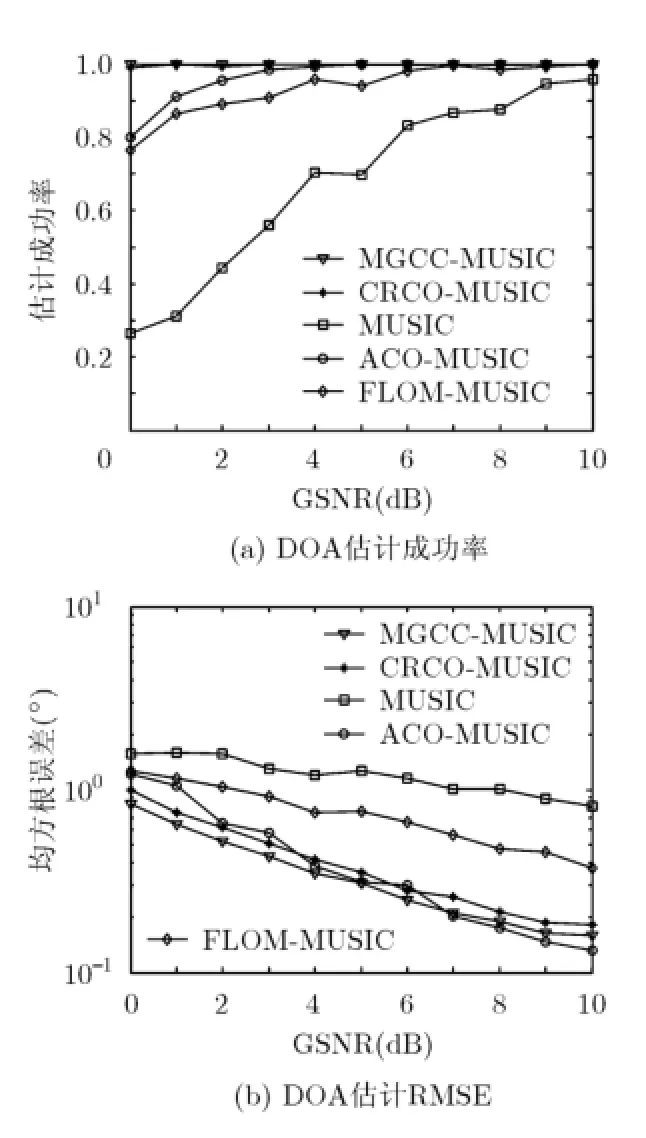
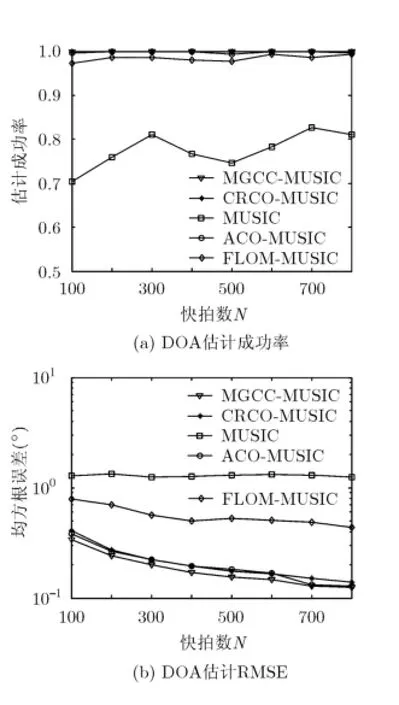
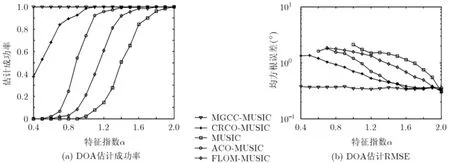
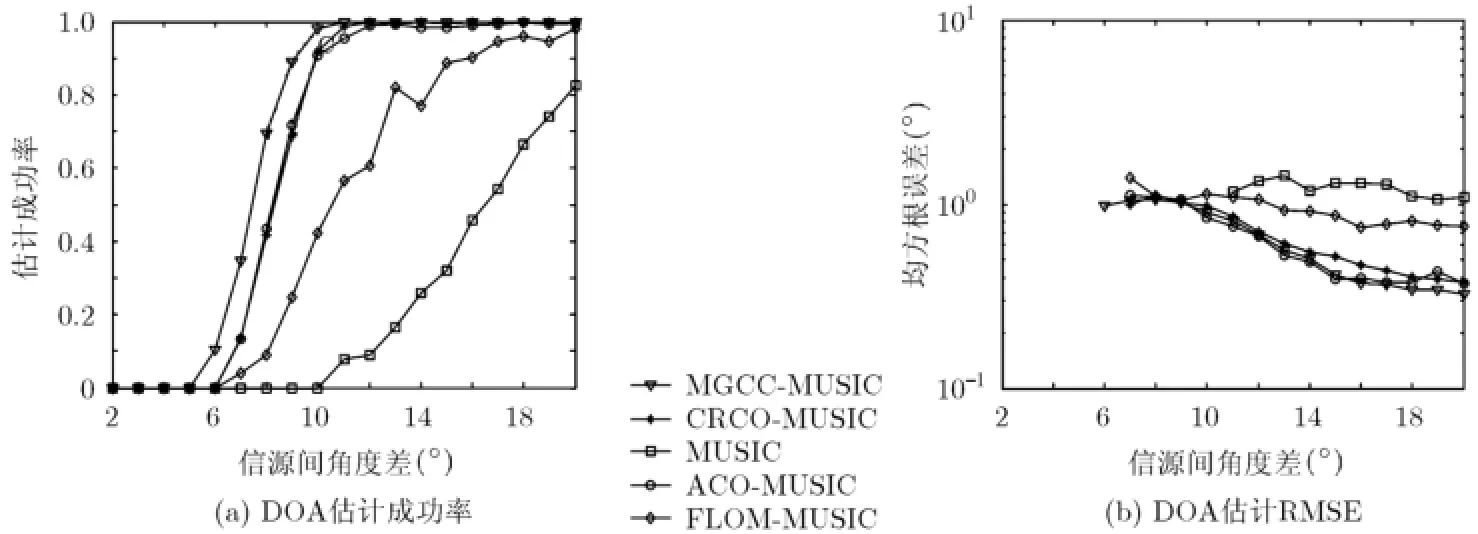
为抑制A lpha稳定分布噪声的影响,文献[4-8]提出了基于分数低阶统计量(Fractional Lower Order Statistics,FLOS)的DOA估计方法。该类方法虽取得了较好的估计效果,但存在一定的局限性:(1)阶次p必须满足1≤p<α[4-6]或0 为了更好地抑制脉冲噪声,提高DOA估计算法的鲁棒性,本文定义了一种新的广义相关熵,提出了一种基于最小广义相关熵准则的DOA估计新方法。该方法无需构造协方差矩阵,通过优化算法直接实现信号子空间的估计,为利用相关熵实现DOA估计提供了一种新思路。仿真结果表明,本文算法在高脉冲性噪声环境下能够获得更好的估计结果。 2.1稳定分布 对称A lpha稳定(Symmetric A lpha Stable,SαS)分布随机变量常用其特征函数进行描述[3]。 其中,2α<≤0称为特征指数,用来度量概率密度函数的拖尾厚度,0γ>是分散系数,用以度量样本的分散程度,μ是位置参数,当1 2α<≤时,该参数表示该随机变量的均值,当0 1α<<时,该参数则表示该随机变量的中值。特别地,当2α=时,SαS分布退化为高斯分布。当2α<时,S Sα随机变量不存在有限的二阶矩,因此基于二阶统计量的传统DOA估计算法在稳定分布噪声环境下性能严重退化。 2.2相关熵 相关熵作为一种随机变量局部相似性的度量[13],广泛应用于时延估计[14]、自适应滤波[15,16]、图像处理[17]以及医学信号处理[18]等领域,其定义为 3.1问题描述 假设均匀等距线阵由M个阵元组成,阵元间距为d,存在P个频率已知的窄带信源,信源之间相互独立,入射角度分别为θ1,θ2,…,θP,以第1个阵元为参考阵元,则第m个阵元t时刻的输出可以表示为 其中,si(t)为第i个信源的复包络,λ表示信号波长且满足d≤λ/2,nm(t)表示服从SαS分布的加性噪声,各阵元噪声相互独立,噪声与信号之间相互独立。进一步将式(5)写成矩阵形式: 根据低秩近似理论[19],X可以利用低秩矩阵X进行近似: 其全局最优解如下: 其中,SVD(·)表示奇异值分解,Ds是由P个最大奇异值组成的对角矩阵,Us和Vs分别为对应的左特征向量和右特征向量。由矩阵相关理论可知,矩阵Us与A张成相同的子空间。将式(8)的代价函数进一步写为 由于服从S Sα分布的随机变量不具有有限的二阶矩,基于式(11)算法的性能必然下降。 3.2广义相关熵 为抑制稳定分布噪声的影响,受相关熵启发,本文定义了一种新的广义相关熵: 可以证明,对称稳定分布随机变量的广义相关熵是有界的。 定理1假设存在两个独立同分布的对称稳定分布随机变量X和Y,定义r X Y=-,则广义相关熵是有界的。 证明根据广义相关熵的定义可知 由S Sα分布的性质[3]可知,r X Y=-同样服从S Sα分布。根据数学期望的定义,式(15)可进一步写为 其中,()f r表示随机变量的概率密度函数。 根据概率密度函数与特征函数之间的关系,将式(1)所示的特征函数代入,可得 又因为 所以,式(17)可以进一步简化为 3.3基于最小广义相关熵准则的DOA估计算法 利用广义相关熵替换式(11)中的二阶矩,本文提出如式(21)所示的代价函数。 为了更好说明广义相关熵对稳定分布噪声的抑制作用,将式(21)进一步写为 其中,B C⊙表示矩阵对应元素相乘,1/2B表示对矩阵中每个元素进行开方运算,R为残差矩阵,W为加权矩阵,其第m行n列元素 图1给出了核长1σ=时的加权因子。从图中可以看出,当残差较大时,加权因子迅速趋于0,可以有效抑制稳定分布噪声中的野点。 利用最小广义相关熵准则(M inimum Generalized Correntropy Criterion,MGCC),最小化式(21)就可以实现信号子空间的估计进而实现空间谱的估计: 图1 加权因子幅度图 3.4算法实现步骤 对比式(22)和式(11)发现可利用奇异值分解实现最小化式(21)的求解,但是由于加权矩阵W与待求解矩阵Y和Z有关,无法单次获得最优解,因此本文采用IR-SVD[12]方法,主要步骤如下:步骤1随机生成列满秩矩阵Y(0)与行满秩矩阵设定迭代次数k=0,初始误差为,迭代停止误差sε以及最大迭代次数K; 步骤6按式(24)计算空间谱,通过搜索峰值实现P个信源DOA的估计。 其中,s(t)表示信号,γ为噪声的分散系数。 本文采用两个指标对算法性能进行评价:DOA估计成功率和均方根误差(Root M ean Square E r r o r,RMSE)。当2个信源的入射角度估计误差都不超过3°时,则认为此次DOA估计是成功的。估计成功率是估计成功次数与随机实验次数之比。DOA估计的RMS?E定义为 本文同时仿真了文献[2]中的经典MUSIC算法、文献[5]中基于分数低阶矩的FLOM-MUSIC算法、文献[10]中基于类相关熵的CRCO-MUSIC算法、文献[12]中基于范数的ACO-MUSIC算法以及本文的MGCC-MUSIC算法。 实验1算法收敛性能设定迭代停止条件εs=,K=100。图2给出了不同噪声环境下本文算法的迭代误差、子空间距离以及代价函数的变化曲线。其中,子空间距离定义为从图中可以看出,当迭代误差满足时,子空间距离以及代价函数基本稳定,即以此为迭代停止条件是合适的。 实验2核长的选择图3给出了不同噪声环境下算法性能随核长σ的变化曲线,其中快拍数N=100。可以发现,当核长满足σ∈[1.3,2.5]时,本文算法可以达到较好的估计结果。因此,在后续仿真实验中,核长参数均取σ=1.5。此外,还可以发现,当噪声的特征指数对算法性能影响很小。 图2 算法迭代收敛曲线 实验3 GSNR对算法性能的影响图4给出了不同GSNR下的估计结果,其中噪声的特征指数α=1.5,快拍数N=100。可以看出,随着GSNR的提高,所有算法性能均有显著提高。与其它4种算法相比,经典MUSIC算法在稳定分布噪声环境下的性能较差。在低信噪比环境下,MGCC-MUSIC算法与CRCO-MUSIC算法可以获得更高的估计成功率,而且MGCC-MUSIC算法具有更低的估计误差;而在高信噪比环境下,MGCC-MUSIC算法则与ACO-MUSIC算法性能相当。 实验4快拍数对算法性能的影响图5给出了快拍数N对算法性能的影响。设定SαS噪声特征指数α=1.5,GSNR为4 dB。可以发现,除经典MUSIC算法外,其它4种算法的RMSE均随着快拍数的增加而减小,其中MGCC-MUSIC,CRCO-MUSIC以及ACO-MUSIC 3种算法的估计成功概率相近,但是MGCC-MUSIC算法可以获得更低的估计误差。 实验5稳定分布噪声特征指数的影响图6给出了不同噪声特征指数下算法的估计结果,其中快拍数N=100,GSNR为4 dB。可以看出,在高脉冲性噪声环境下,本文算法具有非常明显的优势。此外,与图2和图3现象一致,噪声特征指数α对本文算法性能的影响较小。 实验6角度分辨率图7给出了不同算法的角度分辨能力。信源1的入射角度1θ从0°变化至18°,信源2的入射角度固定为220θ=°,噪声特征指数1.5α=,GSNR为4 dB。从图中可以看出,本文算法能够分辨的最小角度差为6°,优于其它算法。此外,还可以发现,当两个信源的角度差较小时,本文方法的估计成功率更高,而当两个信源的角度差较大时,本文方法则在RMSE方面具有微弱的优势。 图3 算法性能随核长的变化曲线 图4 算法性能随GSNR的变化曲线 图5 算法性能随快拍数的变化曲线 图6 算法性能随特征指数的变化曲线 图7 算法的角度分辨率 本文定义了一种新的广义相关熵,证明了对称稳定分布随机变量广义相关熵的有界性,并基于最小广义相关熵准则提出了一种稳定分布噪声下的DOA估计新方法。该方法无需构造协方差矩阵,通过求解优化问题直接实现信号子空间的估计。为实现优化问题的求解,本文给出了一种迭代优化算法,并通过仿真实验分析了算法的收敛性。最后,本文分析了核长、广义信噪比、快拍数、噪声特征指数以及信源间入射角度差对算法性能的影响。仿真结果表明,本文算法可以获得更好的估计结果,尤其是在高脉冲性噪声环境下具有更加明显的优势。 [1]KRIM H and VIBERGM.Twodecadesofarray signalprocessing research:the parametric approach[J].IEEE Signal Processing Magazine,1996,13(4):64-97.doi:10.1109/79.526899. [2]SCHM IDE R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280.doi:10.1109/tap.1986.1143830. [3]SHAO M and NIKIAS C L.Signal processing with fractional lower ordermoments:stable processes and their applications[J]. Proceedings of the IEEE,1993,81(7):986-1010.doi: 10.1109/5.231338. [4]TSAKALIDESP and NIKIASC L.The robust covariation-based MUSIC(ROC-MUSIC)algorithm for bearing estimation in impulsive noise environments[J].IEEE Transactions on Signal Processing,1996,44(7):1623-1633.doi:10.1109/78.510611. [5]LIU T and MENDEL JM.A subspace-based direction finding algorithm using fractional lower order statistics[J].IEEE Transactions on Signal Processing,2001,49(8):1605-1613.doi: 10.1109/78.934131. [6]ZHANG JF and QIU T S.A novel covariation based noncircular sources direction finding method under impulsive noise environments[J].Signal Processing,2014,98:252-262.doi: 10.1016/j.sigpro.2013.11.031. [7]BELKACEM I H and MARCOS S.Robust subspace-based algorithms for joint angle/Doppler estimation in non-Gaussian clutter[J].Signal Processing,2007,87(7):1547-1558.doi: 10.1016/j.sigpro.2006.12.015. [8]YOUG H,QIU T S,and SONG AM.Noveldirection findings for cyclostationary signals in im pulsive noise environments[J]. Circuits,System s,and Signal Processing,2013,32(6):2939-2956. doi:10.1007/s00034-013-9597-0. [9]张金凤,邱天爽,宋爱民,等.Alpha稳定分布噪声环境下类M估计相关的DOA估计新算法[J].通信学报,2013,34(5):71-78.doi: 10.3969/j.issn.1000-436x.2013.05.008. ZHANG Jinfeng,QIU Tianshuang,SONG Aim in,et al. M-estimate like correlation based algorithm for direction ofarrival estimation under alpha-stable environm ents[J].Journal on Communications,2013,34(5):71-78.doi: 10.3969/j.issn.1000-436x.2013.05.008. [10]ZHANG J F,QIU T S,SONG A M,et al.A novel correntropy based DOA estimation algorithm in impulsive noise environments[J].Signal Processing,2014,104:346-357.doi: 10.1016/j.sigpro.2014.04.033. [11]邱天爽,张金凤,宋爱民,等.脉冲噪声下基于广义类相关熵的DOA估计新方法[J].信号处理,2012,28(4):463-466. QIU Tianshuang,ZHANG Jinfeng,SONG Aimin,et al.The generalized correntropy-analogous statistics based direction of arrival estimation in impulsive noise environments[J].Signal Processing,2012,28(4):463-466. [12]ZENG W J,SO H C,and HUANG L.lp-MUSIC:Robust direction-of-arrivalestimator for impulsive noise environments[J]. IEEETransactionson SignalProcessing,2013,61(17):4296-4308. doi:10.1109/tsp.2013.2263502. [13]LIU W F,POKHAREL P P,and PRINCIPE J C.Correntropy: properties and app lications in non-Gaussian signal processing[J]. IEEETransactionson SignalProcessing,2007,55(11):5286-5298. doi:10.1109/tsp.2007.896065. [14]宋爱民,邱天爽,佟祉谏.对称稳定分布的相关熵及其在时间延迟估计上的应用[J].电子与信息学报,2011,33(2):494-498.doi: 10.3724/SP.J.1146.2010.00309. SONG Aim in,QIU Tianshuang,and TONG Zhijian.Correntropy of the symmetric stable distribution and its application to the time dealy estimation[J].Journal of Electronics&Information Technology,2011,33(2):494-498.doi: 10.3724/SP.J.1146.2010.00309. [15]WU Z Z,SHIJ H,ZHANG X,et al.Kernel recursivemaximum correntropy[J].Signal Processing,2015,117:11-26.doi: 10.1016/j.sigpro.2015.04.024. [16]CHEN B D,LEIX,LIANG J L,etal.Steady-statemean-square error analysis for adaptive filtering under the maximum correntropy criterion[J].IEEE Signal Processing Letters,2014,21(7):880-884.doi:10.1109/LSP.2014.2319308. [17]WANG L F and PAN C H.Robust level set image segm entation via a local correntropy-based K-means clustering[J].Pattern Recognition,2014,47(5):1917-1925.doi: 10.1016/j.patcog.2013.11.014. [18]MELIA U,GUAITA M,VALLVERDU M,et al.Correntropy measures to detect daytim e sleepiness from EEG signals[J]. Physiological Measurements,2014,35(10):2067-2083.doi: 10.1088/0967-3334/35/10/2067. [19]MARKOVSKY I.Low Rank Approximation:Algorithms,Im plementation,Applications[M].London,UK,Springer-Verlag London,2011:60-64. 王鹏:男,1989年生,博士生,研究方向为阵列信号处理、非高斯非平稳信号处理. 邱天爽:男,1954年生,博士,教授,博士生导师,主要研究方向为非平稳非高斯统计信号处理、数字信号处理等. 任福全:男,1984年生,博士生,研究方向为图像处理、成像与压缩感知等. 李景春:男,1966年生,博士,高级工程师,主要研究方向为无线电监测理论与应用等. 谭海峰:男,1977年生,高级工程师,主要研究方向为无线电频谱工程以及无线电监测等. A Novel Generalized Correntropy Based Method for Direction of Arrival Estimation in Symmetric Alpha Stable Noise Environments WANG Peng①QIU Tianshuang①REN Fuquan①LIJingchun②TAN Haifeng②③① To overcome the lim itation that the alpha stab le distributed variable possesses infinite second-order moment,a novelgeneralized correntropy is defined and thebounded property of the generalized correntropy for the symmetric alpha stab le variable is proved.Furthermore,a novelm inimum generalized correntropy criterion based DOA estim ation method for im pu lsive noise is proposed,and an iterative optim ization algorithm is presented,the convergence ofwhich is analyzed by simulation experiments.The simulation resu lts demonstrate that the proposed method can get better estimation resu lts than the fractional lower order moments based FLOM-MUSIC,the correntropy-like based CRCO-MUSIC and the lp norm based ACO-MUSIC methods,especially in the highly im pulsive noise environments. Direction O f Arrival(DOA)estimation;Correntropy;Generalized correntropy;A lpha stable distribu ted noise;MUSIC algorithm s:The National Natural Science Foundation of China(61139001,61172108,81241059) TN911.7 A 1009-5896(2016)08-2007-07 10.11999/JEIT 151217 2015-11-03;改回日期:2016-03-03;网络出版:2016-05-09 邱天爽qiutsh@d lut.edu.cn 国家自然科学基金(61139001,61172108,81241059)2 稳定分布与相关熵
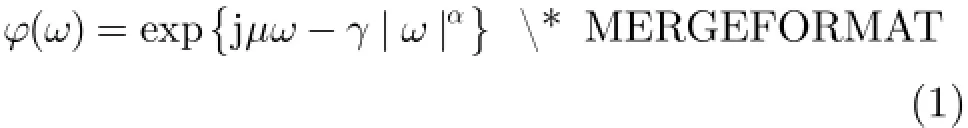
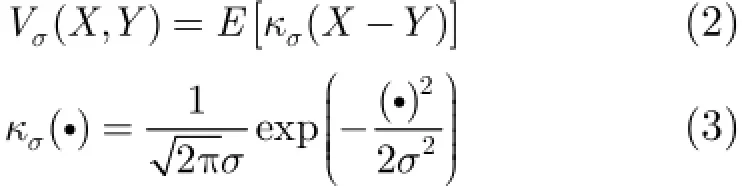
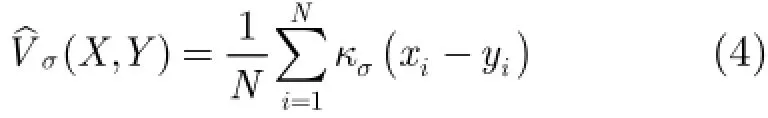
3 基于广义相关熵的DOA估计
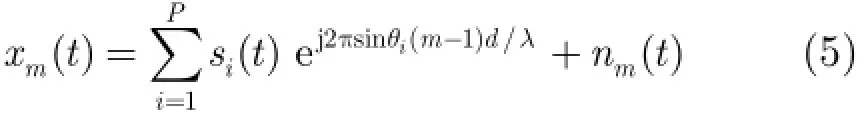

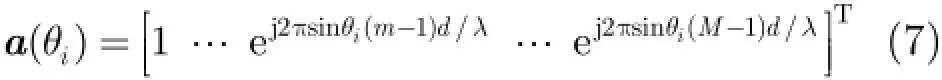
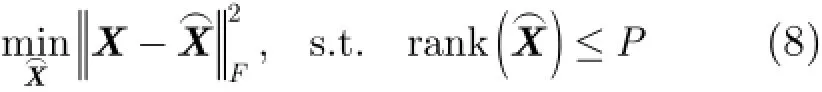
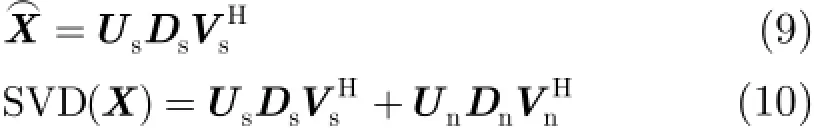
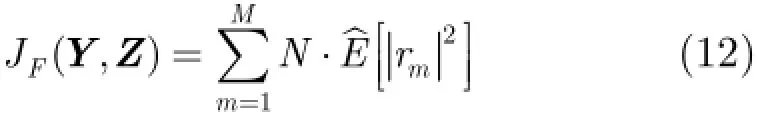
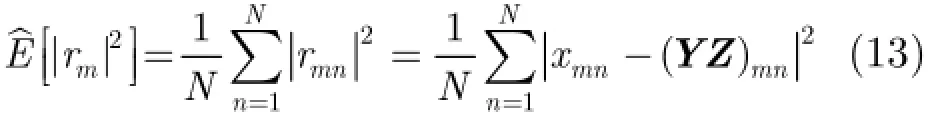
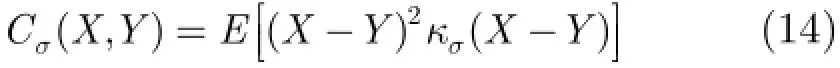
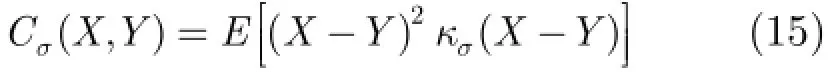
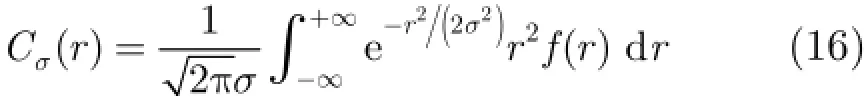
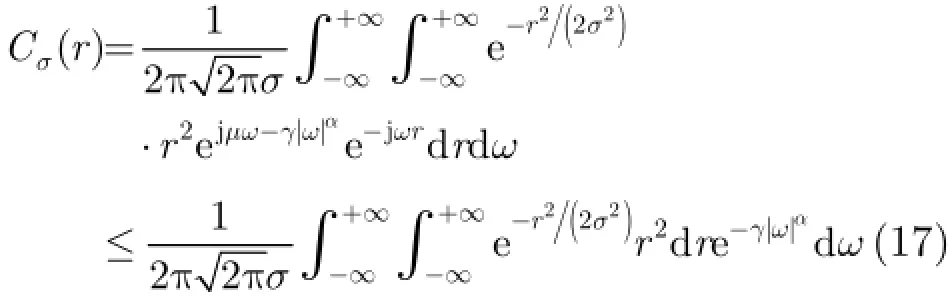
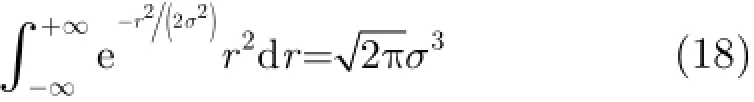

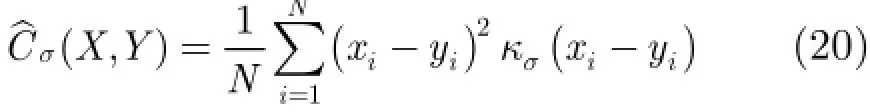
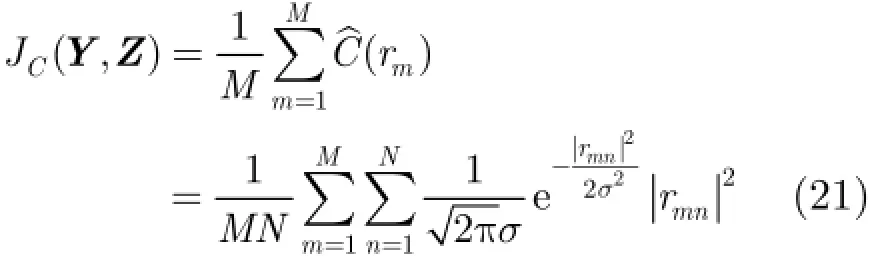
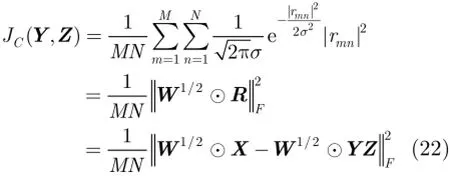
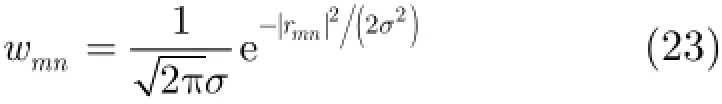
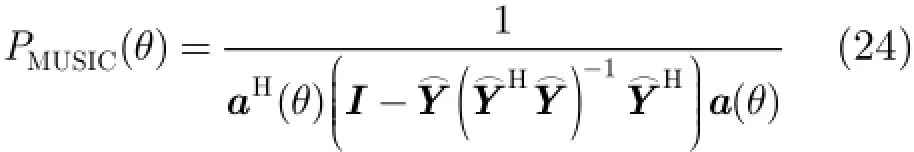
4 仿真实验
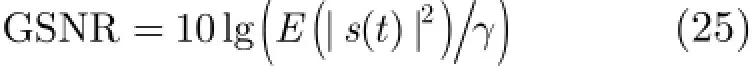

5 结论
①(Faculty ofElectronic Information and Electrical Engineering,Dalian University of Technology,Dalian 116024,China)
②(State Radio Monitoring Center,Beijing 100037,China)
③(Schoo l of Inform ation and Communication Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China)
