Feistel-SPS结构的反弹攻击
2016-08-30吴文玲河南师范大学大数据统计分析与优化控制河南省工程实验室新乡453007河南师范大学数学与科学计算重点学科开放实验室新乡453007福州大学数学与计算机科学学院福州350116中国科学院软件研究所可信计算与信息保障实验室北京100190
董 乐 邹 剑 吴文玲 杜 蛟(河南师范大学大数据统计分析与优化控制河南省工程实验室新乡453007)(河南师范大学数学与科学计算重点学科开放实验室新乡453007)(福州大学数学与计算机科学学院福州350116)(中国科学院软件研究所可信计算与信息保障实验室北京100190)
Feistel-SPS结构的反弹攻击
董乐*①②邹剑③吴文玲④杜蛟①②①
①(河南师范大学大数据统计分析与优化控制河南省工程实验室新乡453007)
②(河南师范大学数学与科学计算重点学科开放实验室新乡453007)
③(福州大学数学与计算机科学学院福州350116)
④(中国科学院软件研究所可信计算与信息保障实验室北京100190)
该文给出了以Feistel结构为主框架,以SPS(Substitu tion-Perm utation-Substitution)函数作为轮函数的Feistel-SPS结构的反弹攻击。通过对差分扩散性质的研究,得到这一结构的6轮已知密钥截断差分区分器,并在此区分器的基础上,给出将这一结构内嵌入MMO(M atyas-Meyer-Oseas)和MP(M iyaguchi-Preneel)模式所得到的压缩函数的近似碰撞攻击。此外,还将6轮截断差分区分器扩展,得到了7轮的截断差分路径,基于此还得到上述两种模式下压缩函数的7轮截断差分区分器。
反弹攻击;Feistel结构;SPS(Substitution-Permutation-Substitution)函数;截断差分区分器;近似碰撞
2011年,文献[10]构造了11轮Feistel-SP结构的已知密钥区分器,并用其构造了这一结构杂凑模式的近似碰撞攻击。2012年,文献[11]将这一方法用于分析以SP函数为轮函数的type-1,type-2和type-3广义Feistel结构。2014年,文献[12]将type-1广义Feistel结构的结果加以改进,次年文献[13]又将type-2广义Feistel结构的结果加以改进。双SP函数提出后,文献[14]比较了type-2广义Feistel结构下的单SP函数与双SP函数,构造出了含更多SP层的区分器,从而得出在反弹攻击下双SP函数模型更弱的结论。
本文首次对以SPS函数为轮函数的Feistel结构(Feistel-SPS结构)实施反弹攻击,将适用于AES型轮函数的“非全活跃状态的差分匹配技术”首次用于“单列SPS结构”中,得到了6轮的已知密钥区分器,并基于这一区分器构造了其杂凑模式的6轮近似碰撞攻击。然后又将这一区分器加以改进,得到了7轮的已知密钥区分器,并得到其压缩函数的7轮已知密钥区分器。
本文第2节介绍了相关的背景知识;第3节对6轮Feistel-SPS结构进行反弹攻击;第4节对7轮Feistel-SPS结构进行反弹攻击;第5节总结全文。
2 基本知识
2.1 Feistel-SPS结构
首先给出一些符号记法:N为密码算法的分组长度;n为Feistel结构中左半部分或右半部分比特数,即n=N/2;c为S盒所包含的比特数;r为轮函数中一个S盒层所含S盒的个数。
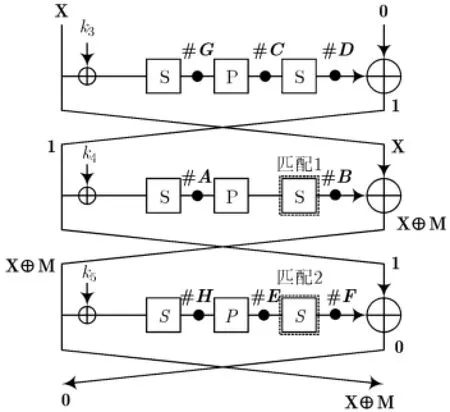
Feistel-SPS结构如图1所示,它采用了经典的Feistel网络作为它的结构,而轮函数采用了SPS结构。
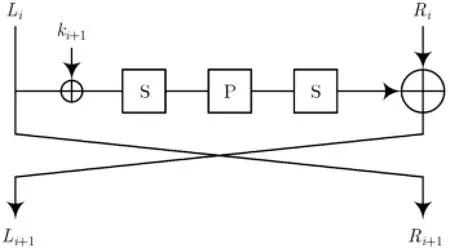
图1 Feistel-SPS结构的一轮
假定文中所攻击的Feistel-SPS结构,除子密钥之外每一轮都是相同的,并且S盒层和P层具有“好”的密码学特性,即轮函数中两个S盒层的每一个S盒具有最优的抵抗差分分析与线性分析的密码学特性。对于差分分析来说,它们均有最优的差分扩散性,即任一S盒的每一个输入差分都有2c-1个可能的输出差分与其对应,这样任意一对输入输出差分可以在这一S盒层达到匹配的概率就是1/2,而一旦达成匹配,有两对输入输出值与其对应;此外,轮函数中P层的分支数达到最大,即r+1。
2.2反弹攻击
2009年,文献[15]提出一种针对AES类杂凑函数的攻击方法,这一攻击方法的攻击过程分为弹入部分和弹出部分,所以命名为“反弹攻击”。反弹攻击的最终目的是以比穷举攻击更低的复杂度找到满足某一预设截断差分特征的一对值,从而得到区分器或者得到一对(近似)碰撞。
由于AES类杂凑函数的轮函数中,S盒往往具有最优差分扩散特点,而线性扩散层则具有最大的分支数,所以对差分分析有很强的抵抗能力。但如果确定输入输出差分,也能够在这样的S盒处以最大(1/2)的概率实现差分匹配。正是利用这一点,反弹攻击在弹入部分可以有效地得到许多满足这一部分截断差分特征的值。利用这些值,攻击者可以以一定的概率实施弹出攻击,从而得到满足整个截断差分路径的值。本文的7轮攻击采用了传统的弹入攻击模式,而6轮攻击则采用了非全活跃差分匹配[16]的方法进行弹入攻击,都取得了预期的效果。
2.3MMO模式与MP模式
设EK是一个密钥为K的分组密码算法,M为消息块,H为中间链值,MMO模式的压缩函数计算过程为

MP模式的压缩函数计算过程为
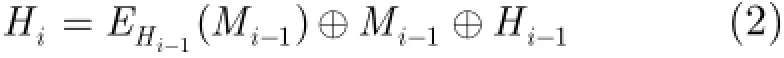
本文基于6轮已知密钥截断差分区分器,构造了内嵌Feistel-SPS结构(即分组密码KE具有这一结构)的MMO模式和MP模式的近似碰撞。
3 Feistel-SPS结构的6轮反弹攻击
本节以4r=,8c=的Feistel-SPS结构为例,对其进行6轮(含有12个S盒层)的反弹攻击。
3.1攻击概述
首先,给出攻击中所使用的几个符号:
0为所有字节都不活跃的字;i为有i个指定位置的字节是活跃的字,例如2表示有两个指定位置的字节是活跃的字;F为全部字节都活跃且不能确定其差分的字。
攻击的第1步利用反弹攻击对Feistel-SPS结构构建一条6轮差分路径,其中第3轮和第4轮为弹入部分,第1轮和第2轮为逆向弹出部分,第5轮和第6轮为正向弹出部分。整个差分路径的差分传播模式为
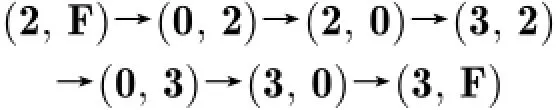
最后得到了82对满足整个6轮差分路径的值,以这些值构造内部置换采用Feistel-SPS结构,反馈采用MMO或MP模式的压缩函数的近似碰撞。
3.2两轮弹入部分
这一部分将构建截断差分特征相“对称”的两个弹入轮,并最终找到一对满足差分传播模式的值。
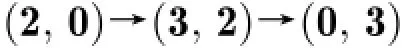
如图2所示,具体的攻击过程为:
步骤1选择#A处4个字节中的前2个作为活跃字节,并确定这2个活跃字节的差分。
步骤2选择#B处4个字节中的前3个作为活跃字节,并将其前2个活跃字节的差分设定为与#A处前2个字节差分相同,第3个字节的差分暂不确定(图3中浅灰色的字节)。
步骤3现在连接此轮轮函数的输入输出差分,并确定满足这一差分路径的值,具体如下(如图3所示):

图2 两轮弹入部分
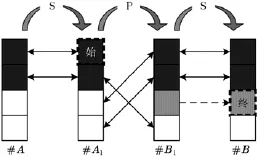
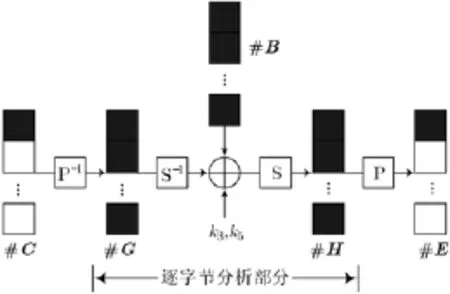
图3 轮函数差分匹配部分
(1)对#A,#B处的每一个确定差分的活跃字节,遍历其所有28个值,进行S盒与逆向S盒的计算,然后将这些值和其对应的输出差分同时存储在一个表中,并以输出差分进行索引。最后共可得到4个这样的表。
(2)从状态#A1的第1个字节开始,从#A的第1个字节通过S盒层之后的所有可能的输出差分中选择一个,作为#A1的第1个字节的差分。
(3)此时,在P层的输入状态中,1个活跃字节的差分确定,另有2个非活跃字节差分也确定(零差分),加上输出P层的输出状态中有1个非活跃字节,这样,P层的输入输出状态共有4个字节的差分是确定的。用解方程组的方式计算出另外4个活跃字节的差分。
(4)在#A与#A1的第2个字节之间谋求差分匹配,同时在#B与#B1的前两个字节之间谋求差分匹配,全部匹配的概率为2-3,所以可以在选择#A1第1个字节的23个差分(第(2)步)之后期望找到这3个字节差分的全匹配。注意到#A与#A1的第1个字节的差分总是可以匹配的,此时得到了4个活跃字节之间的差分匹配,从而可以确定它们所对应的值。由于一个字节的差分匹配有两对值与其对应,所以共得到24对满足差分路径的值。
(5)从这些值中选择一个,在P层建立值之间的连接,这里将使用非活跃字节值的自由度。利用解方程的方式,由已经确定的#B1中两个活跃字节(图3中深灰色字节)的值,计算#A1中两个非活跃字节的值,使P层的输入输出值不产生矛盾;同样,由已经确定的#A1中第2个活跃字节的值,计算#B1中唯一一个非活跃字节的值,使P层的输入输出值不产生矛盾。
(6)最后,利用#A1的整个状态值,计算#B1中浅灰色字节的值(其差分在第(3)步已经确定),并计算与其对应的#B中的第3个字节的差分和值。注意这里#B处的第3个字节是唯一不可预设差分的字节,也就是说最后这一字节的差分是无法控制的。
(7)取遍#A1第1个字节差分的所有27情况,每一种情况都进行第(2)步-第(6)步的迭代。注意到在第(4)步中,每选择#A第1个字节处的一个差分,平均可以得到两对满足差分路径的值,而取每一个值都可以得到一个#B的第3个字节的差分和其对应的一对值,所以最后可以得到#B的第3个字节的28个差分,将此差分与其对应的#A,#B处的值存储在一个表中,用此差分作为索引。
步骤4选择#D处4个字节中的前两个作为活跃字节,并将这两个活跃字节的差分设定为与#A处前两个字节差分相同。
步骤5选择#C处4个字节中的前3个作为活跃字节,并将其前两个活跃字节的差分设定为与#B处前两个字节差分相同,第3个字节的差分同样暂不确定。
步骤6利用与步骤3类似的方法,将这一轮函数的输入输出差分连接起来,并确定满足这一差分路径的值。最后也得到#C的第3个字节的82个差分,同样将此差分与其对应的#A,#B处的值存储在一个表中,用此差分作为索引。
步骤7对#B处和#C处的第3个字节的差分进行中间相遇攻击(前两个字节的差分已经设定为相同)。在步骤3和步骤6,两处的第3字节均有82个差分,所以共有88162 2=2×个差分对,两差分相同的概率为所以期望找到个单字节碰撞。
步骤8对于每一个碰撞,均有#B和#C处的差分相同,这样第1弹入轮与第2弹入轮的差分就可以成功连接;而且#A与#D处的差分相同,这样第2弹入轮右侧异或运算的结果为一个零差分状态。
至此,找到了28对满足这两轮差分路径的值。
这一部分的复杂度分析如下:首先步骤1、步骤2的复杂度可以忽略。在步骤3中,(1)中构造4个表需用去4×28=210次S盒或逆向S盒的计算,和210字节的存储;(2)-(5)中的解方程和查表运算的复杂度均可忽略;在(6)中,需要计算浅灰色字节的值与差分,然后存储,所以进行两次S盒的计算和一个字节存储;而(7)中进行27次(2)中-(6)中的迭代,每次迭代只有(6)中产生时间复杂度与存储消耗,所以共需2×27=28次S盒计算和27字节的存储。至此,步骤3的计算复杂度约为4×28=210次S盒或逆向S盒的计算,存储约为210字节。步骤4-步骤6的计算复杂度与前3步相同,并且与前3步独立计算,所以共需约2×210=211次S盒计算和211字节的存储。步骤7利用查表进行的中间相遇攻击的复杂度可以忽略。
综上所述,两轮的弹入部分共需约2×210=211次S盒计算和211字节的存储,相当于25.4次6轮运算和28的全状态存储。
3.3弹出部分
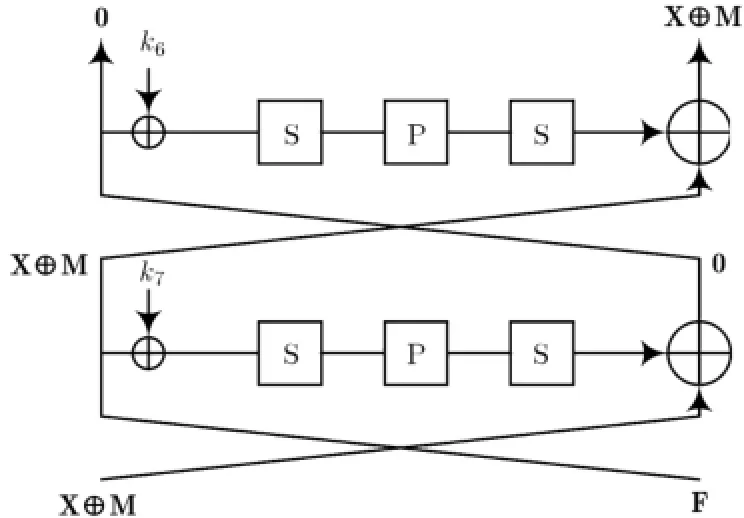
在两轮弹入部分的前后各加两轮,得到共涉及6轮的反弹攻击,即两弹入轮为第3,4轮,其前面有两轮逆向弹出部分,后面有两轮正向弹出部分,这两部分概率都为1。逆向与正向弹出部分分别如图4和图5所示。
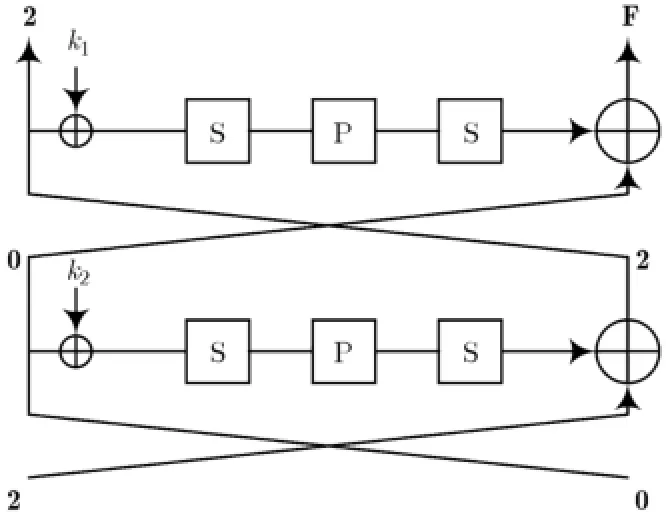
图4 6轮攻击的逆向弹出部分
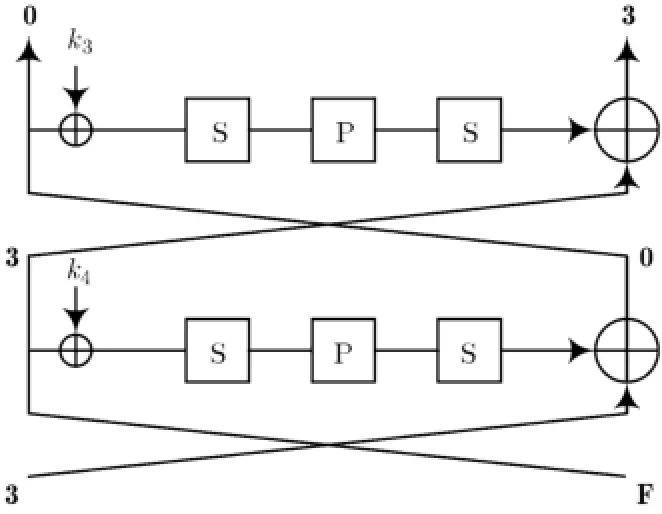
图5 6轮攻击的正向弹出部分
值得注意的是,6轮差分路径的输入(2,F)与输出(3,F)的左半部分的前两个字节的差分是相同的。而在弹入部分共得到28对满足差分模式(2,0)→(3,2)→(0,3)的值,所以最后也可以得到28对满足6轮差分路径的值。而进行28次弹出部分攻击的复杂度为29次4轮计算,约为28.4次6轮计算。
3.4攻击扩展到所有参数
前面所述的反弹攻击可以看作是对一个分组密码或者一个杂凑函数的内部置换构造了一个(已知密钥)区分器。由弹入与弹出攻击的过程可知,弹入部分的复杂度为2c-2.6,弹出部分的复杂度为2c+0.4,所以总体的复杂度约等于2c+0.4,得到了2c对满足输入差分模式为(r/2,F),输出差分模式为((r/2)+1,F)的值,其中输入差分模式的左半部分有r/2个差分为零的字节,另外r/2个差分为预设值的字节,输出差分模式的左半部分有r/2-1个差分为零的字节,另外r/2个差分为预设值的字节,所以只有一个字节的差分是不确定的。按照生日攻击的复杂度,得到2c对满足此输入输出差分的值需要2(n-c)/2×2c的复杂度。所以,攻击有效需要满足条件2c+0.4<2(n-c)/2×2c,即c 3.5两种压缩函数模式的近似碰撞攻击 当某些压缩函数的内部置换采用Feistel-SPS结构,其反馈采用MMO或MP模式的时候,这一攻击还可以用来构造近似碰撞。注意到,区分器的输入差分模式(r/2,F)和输出差分模式((r/2)+1,F)中,左半部分有(/2)r-byte的差分是对应相同的,这样经过输入与输出的异或运算,可以将(/2)r-by te的差分消去,最后得到的压缩函数的输出具有差分模式(1,F),即得到了()n c--bit的近似碰撞。而上节共得到了2c对满足6轮差分路径的值,则最后可以得到2c个近似碰撞,依概率可以期望得到n-bit的近似碰撞,即半个状态的碰撞。 4.1攻击概述 本节以8r=,8c=的Feistel-SPS结构为例,利用反弹攻击构造一条7轮的截断差分路径。在整个7轮的反弹攻击中,弹入部分有3轮,在这3轮弹入部分的基础之上,前面加上两个逆向弹出轮,后面加上两个正向弹出轮,构成整个7轮差分路径。7轮截断差分模式可以表示为 在这里,X是某一中间确定的全活跃字差分,M是某一提前给定的全活跃字差分。 根据这一路径的性质:将输入差分与输出差分异或,所得状态的左半部分为提前给定的全活跃字差分M。以7轮的Feistel-SPS结构作为内部置换,外部以MMO或MP模式作为反馈结构构造压缩函数,其输出的一半为某一提前设定的全活跃字差分。 4.2 3轮弹入部分 3轮弹入部分的截断差分路径为 如图6所示,攻击的详细过程为: 步骤1对轮函数中第2个S盒层的所有S盒建立“差分分布表”。 步骤2设定#B处的差分为提前给定的差分M。 图6 7轮攻击的弹入部分 步骤3在#A处选择1个字节作为活跃字节(不妨选择第1个字节),则#A处的差分模式为1。随机选择#A处活跃字节的差分值得Δ#A,计算,然后通过查表在图6中“匹配1”处检查P(Δ#A)和Δ#B是否能在这里的S盒层建立匹配。由于每个字节差分匹配的概率为1/2,所以期望选择28个#A处活跃字节的差分值可以在“匹配1”处找到一个匹配。而由于每一个匹配的字节都有两对值满足匹配的输入输出差分,所以这里共有28对值满足#A处到#B处的差分特征。 步骤4从这28对值中选择一个,由处计算逆向S盒,再异或子密钥k4,得第2弹入轮左半部分状态的差分和值,这样就确定了处和处的差分,而其值暂时不确定。 (1)注意到#G是全活跃的,对于#G的每一个字节,遍历其全部的28个值,对每个值计算至#H处,检查其对应的差分是否与#H处对应字节的差分相等,若相等存储其对应的#G处和#H处的值。 (2)对于#H处每一个字节存储值的每一个组合,计算#E处值,并计算其通过S盒层之后所对应的差分是否等于前面已确定的#F处第1个字节的差分,如果相等则成功地在“匹配2”处建立了差分匹配。利用同样的方法建立#C的活跃字节与#D的活跃字节的差分匹配。 图7 字节级差分匹配部分 (3)如果不能同时找到#C与#D处、#E与#F处活跃字节的差分匹配,则需要从#C与#E处的27种差分中再选择,进行(1)-(2)步中的计算,直到找到#C与#D处、#E与#F处活跃字节的差分匹配为止。 步骤6记录下匹配上的差分所对应的值,计算出所对应的整个弹入部分输入与输出的值。 这样就找到了一对满足弹入部分3轮差分特征的值,这一部分的复杂度分析如下:在步骤1建立差分分布表共需28×28×8=219次S盒计算。步骤2-步骤3查表的复杂度可忽略不计。步骤4需要1次逆向S盒的计算。在步骤5的(1)中,每个字节的差分匹配上的概率为2-8,即需要28的复杂度建立一个匹配,所以每个字节的28对值可以期望找到1个匹配,这1个匹配的值可以有两种配对情况,故8个字节共有28对值满足#G到#H处的差分,得到这28对值共需28×2×8=212次S盒计算;在步骤5的(2)中,在#C和#D处、#E和#F处建立差分匹配需要216的复杂度,这需要将步骤5的(1)中迭代216-8=28次,每次迭代在步骤5的(1)中需212次S盒计算,故共需212+8=220次S盒计算,与此相比,步骤5的(2)中计算量可忽略不计。所以弹入部分共需要219+1+220≈220次S盒计算,相当于220-4/7≈213.2次7轮Feistel-SPS函数计算,而存储基本上等于保存“差分分布表”所需的空间,即28×2/2=215的全状态存储。 4.3弹出部分 在3轮弹入部分的前面和后面各加上两轮,可以得到共有4轮组成的弹出部分,这一部分的概率为1,其细节如图8和图9所示。其原理与3.3节的6轮反弹攻击类似,只是这一次只有一对值参与弹出运算,最后得到一对满足整个7轮差分路径的值。这对值在明文部分的差分为(X,F),在密文部分的差分为,这里M是一个提前预设好的8个字节全活跃差分。 图8 7轮攻击的逆向弹出部分 图9 7轮攻击的正向弹出部分 4.4 7轮区分器 4.3节利用反弹构造一条7轮的差分路径,并找到了满足这一路径的一对值。由弹入与弹出攻击的过程可知,当r≠c+1时,弹入部分的复杂度约为2max(3c-r,2c-1)-2.8,弹出部分的复杂度为1,所以总体的复杂度约等于2max(3c-r,2c-1)-2.8;当r=c+1时,弹入部分的复杂度约为24c-4.8,弹出部分的复杂度为1,所以总体的复杂度约等于24c-4.8。最后得到一对满足输入差分模式为(X,F),输出差分模式为(X⊕M,F)的值。输入差分与输出差分的异或为某一个提前预设的全活跃差分M,按照生日攻击的复杂度,得到一对满足此输入输出差分的值需要2rc/2的复杂度。所以,攻击有效需要满足条件 常见参数的Feistel-SPS设计除4r=,8c=之外都满足这一条件。 当某些压缩函数的内部置换采用Feistel-SPS结构,其反馈采用MMO或MP模式的时候,这一攻击可以作为碰撞攻击或者近似碰撞攻击的一部分。前面构造的7轮区分器的输入差分模式为(X,F),输出差分模式为(X⊕M,F),它们异或之后的差分模式为(M,F),即左半部分是一个预设的全活跃差分。 本文给出了针对Feistel-SPS结构的反弹攻击,这一攻击根据一个6轮的截断差分区分器得到了其压缩函数模式的6轮近似碰撞攻击。将这一结果扩展,得到了此结构的7轮截断差分区分器,并进一步得到了其压缩函数的7轮截断差分区分器。这是Feistel-SPS结构的首个反弹攻击结果,它显示了在此攻击下这一结构既不比Feistel-SP结构强,也不比Feistel-SPSP结构弱的特性。表1给出本文结果与类似结构结果的比较,为密码算法设计者提供了素材,使其可以在更深层地理解这些结构的基础上做出选择。 [1]U.S.Departm ent of Comm erce and National Institute of Standards and Technology.FIPS PUB 46-3[S].1999. [2]WU Wenling and ZHANG Lei.LBlock:a lightweight b lock cipher[C].9th International Conference on Applied Cryptography and Network Security-ACNS 2011,Nerja,Spain,2011:327-344.doi:10.1007/978-3-642-21554-4_19. [3]BOGDANOV A and SHIBUTANI K.Double SP-functions: enhanced generalized Feistel networks[C].16th Australasian Conference on Information Security and Privacy-ACISP 2011,Melbourne,Australia,2011:106-119.doi:10.1007/978-3-642-22497-3_8. [4]SH IBUTAN IK,ISOBE T,H IWATAR IH,et al.Piccolo:an ultra-lightweight blockcipher[C].13th International W orkshop on Cryptographic Hardware and Em bedded System s-CHES 2011,Nara,Japan,2011:342-357.doi: 10.1007/978-3-642-23951-9_23. [5]KNUDSEN L R and RIJMEN V.Known-key distinguishers for some block ciphers[C].13th International Conference on the Theory and Application of Cryptology and Information Security-ASIACRYPT 2007,Kuching,Malaysia,2007: 315-324.doi:10.1007/978-3-540-76900-2_19. [6]BLONDEAU C,PEYRIN T,and WANG L.Known-key distinguisher on full PRESENT[C].35th Annual Cryptology Conference on Advances in Cryp tology-CRYPTO 2015,Santa Barbara,USA,2015:455-474.doi:10.1007/978-3-662-47989-6_22. [7]ANDREEVA E,BOGDANOV A,and MENNINK B. Towards understanding the known-key security of block ciphers[C].20th International Workshop on Fast Software Encryption-FSE 2013,Singapore,2013:348-366.doi:10.1007 /978-3-662-43933-3_18. [8]ZHA Daren,WU Shuang,and WANG Qiongxiao.Im proved known-key distinguisher on round-reduced 3D block cipher[J]. Chinese Journal of Electronics,2015,24(1):199-204.doi: 10.1049/cje.2015.01.033. [9]AOK I K.A property for full CLEFIA-128 detected by a m idd letext distinguisher under the known-key setting[J]. IEICE Transactions on Fundam entals of Electron ics,Communications and Computer Sciences,2014,97(1): 292-297.doi:10.1587/transfun.E97.A.292. [10]SASAKI Y and YASUDA K.Known-key distinguishers on 11-round Feistel and collision attackson itshashingmodes[C]. 18th International Workshop on Fast Software Encryption-FSE 2011,Lyngby,Denmark,2011:397-415.doi:10.1007/ 978-3-642-21702-9_23. [11]HYUNGCHUL K,DEUKJO H,DUKJAE M,et al. Known-key attacks on generalized Feistel schemes w ith SP round function[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,2012,95(9):1550-1560.doi:10.1587/transfun.E 95.A.1550. [12]DONG Le,WU W en ling,WU Shuang,et al.Known-key distinguishers on type-1 Feistel schem e and near-collision attacks on its hashing modes[J].Frontiers of Computer Science,2014,8(3):513-525.doi:10.1007/s11704-014-2412-7. [13]DONG Le,WANG Yanling,WU Wenling,et al.Known-key distinguishers on 15-round 4-branch type-2 generalised Feistel networks w ith single substitution-permutation functions and near-collision attacks on its hashing modes[J]. IET Information Security,2015,9(5):277-283.doi:10.1049/ iet-ifs.2014.0402. [14]SASAKI Y.Double-sp is weaker than single-sp:rebound attacks on Feistel ciphers w ith several rounds[C].13th International Conference on Progress in Cryptology-INDOCRYPT 2012,Kolkata,India,2012:265-282.doi: 10.1007/978-3-642-34931-7_16. [15]MENDEL F,RECHBERGER C,SCHLÄFFER M,etal.The rebound attack:cryptanalysis of reduced W hirlpool and Grøstl[C].16th International Workshop on Fast Software Encryption-FSE 2009,Leuven,Belgium,2009:260-276.doi: 10.1007/978-3-642-03317-9_16. [16]SASAKIY,LIY,WANG L,etal.Non-full-active Super-Sbox analysis:applications to ECHO and Grøstl[C].16th International Conference on Advances in Cryptology-ASIACRYPT 2010,Singapore,2010:38-55.doi:10.1007/ 978-3-642-17373-8_3. 董乐:男,1980年生,博士,副教授,研究方向为分组密码与杂凑函数的分析等. 邹剑:男,1985年生,博士,讲师,研究方向为杂凑函数的设计与分析等. 吴文玲:女,1966年生,博士,研究员,博士生导师,研究方向为分组密码的设计与分析、杂凑函数的研究与应用等. Rebound Attack on the Feistel-SPS Structure DONG Le①②ZOU Jian③WUWenling④DU Jiao①②①(Henan Engineering Laboratory for Big Data Statistical Analysis and Optimal Control,Henan Normal University,Xinxiang 453007,China) This paper shows the rebound attack on the Feistel-SPS structure,which has the Feistel network with a Substitu tion-Perm utation-Substitu tion(SPS)round function.A 6-round known-key truncated differential distinguisher is obtained by studying the d iffusion properties of differences.Based on the distinguisher,a nearcollision attack on the com pression functions of this structure embedding the Matyas-M eyer-Oseas(MMO)and M iyaguchi-Preneel(MP)modes is given.Besides,the 6-round distinguisher is extended and a 7-round truncated differential path is constructed to get a 7-round truncated differential distinguisher of the com pression function for the twomodesmentioned before. Rebound attack;Feistel structure;Substitution-Permutation-Substitution(SPS)function;Truncated differential d istinguisher;Near-collision 在众多现有的攻击技术面前,设计新的安全的对称密码算法并非易事,所以许多设计者更倾向于用一些已被理论证明或者已被时间证明的组件去“组装”一个新的密码算法。常见的组件有“算法结构”和“轮函数结构”。包括分组密码算法DES[1]和LBlock[2]在内的许多算法都采用了(广义)Feistel结构;而大量轮函数采用了SP(Substitution-Permutation)结构。2011年,文献[3]提出了采用“双SP函数”作为轮函数的构想。然而,也有一些密码算法采用所谓的SPS(Substitution-Permutation-Substitution)函数作为轮函数,例如轻量级分组密码算法Piccolo[4],而针对这种SPS结构进行的分析相对缺乏。另一方面,文献[5]提出已知密钥区分器的概念来刻画密码算法或密码结构的非伪随机性,此后出现了许多针对不同算法或结构的已知密钥区分器[69]-。 s:National Natu ral Science Foundation of China(61402154,U 1404601,11471104,11171093),Program for Innovative Research Team(in Science and Technology)in University of Henan Province(14IRTSTHN 023) 表1 3种结构的攻击结果比较 TN918.4 A 1009-5896(2016)08-1928-07 10.11999/JEIT 151255 2015-11-09;改回日期:2016-04-08;网络出版:2016-06-24 董乐dongle127@163.com 国家自然科学基金(61402154,U 1404601,11471104,11171093),河南省高校科技创新团队支持计划(14IRTSTHN023)4 Feistel-SPS结构的7轮反弹攻击



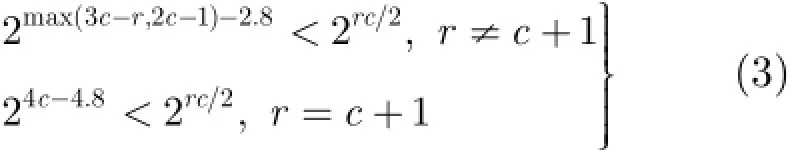
5 结束语
②(Mathematics and Scientific Computing Key-Disciplines Laboratory,Henan NormalUniversity,Xinxiang 453007,China)③(College ofM athematics and Computer Science,Fuzhou University,Fuzhou 350116,China)
④(Trust Computing and Information Assurance Laboratory,Institute ofSoftware,Chinese Academy ofSciences,Beijing 100190,China)1 引言