从头算和ABEEMσπ/MM对(CH3OH)n(n=3～12)和[Na(CH3OH)n]+(n=3～6)体系的研究

于泳博, 刘　翠, 宫利东

(辽宁师范大学化学化工学院, 大连 116029)



从头算和ABEEMσπ/MM对(CH3OH)n(n=3～12)和[Na(CH3OH)n]+(n=3～6)体系的研究

于泳博, 刘翠, 宫利东

(辽宁师范大学化学化工学院, 大连 116029)

采用从头算方法(abinitio)和原子-键电负性均衡浮动电荷分子力场方法(ABEEMσπ/MM), 对甲醇团簇(CH3OH)n(n=3～12)和[Na(CH3OH)n]+(n=3～6)体系的结构、电荷分布和结合能进行研究. 依据从头算结果构建上述体系的ABEEMσπ/MM浮动电荷势能函数, 并确定相关参数. 结果表明, ABEEMσπ/MM所获得的结构和结合能等均优于OPLS/AA力场, 并与从头算结果相符, 其中键长的平均绝对偏差(AAD)小于0.004 nm, 键长、键角和结合能的相对均方根偏差(RRMSD)分别小于3.8%, 1.7%和6.8%; 电荷分布与从头算结果的线性相关系数均大于0.99.

从头算; 原子-键电负性均衡浮动电荷分子力场方法; 甲醇; 钠离子; 分子间相互作用

目前, 溶剂效应是备受关注的研究课题[1]. 与在真空中相比, 分子在溶液中的几何构型、构象、电子结构及其稳定性和光谱性质都会发生不同程度的改变[2～5]. 金属离子溶液广泛存在于自然界、工业技术和生命体等各种物理化学过程中, 已成为溶剂化学领域中最热门的研究方向之一.

甲醇(CH3OH)作为最简单的有机溶剂, 同时含有亲水基团羟基(—OH)和疏水基团甲基(—CH3). 在液态甲醇中, 由于氧原子电负性较强, 甲醇分子可通过分子间氢键形成链状、环状、带支链的环和带支链的链状等多种结构的稳定团簇[6,7]. 当带有正电荷的金属离子进入到液态甲醇中时, 由于金属离子易失去最外层电子而具有空轨道, 甲醇分子中的羟基氧原子具有孤对电子, 所以可形成强相互作用而结合在一起, 导致液态甲醇中原有的氢键结构很大程度上会被影响甚至破坏.

计算模拟已成为研究化学及生命过程的重要工具, 广泛应用于大分子体系的研究中. 理论模拟研究中广泛使用的量子化学计算方法[8,9]由于计算量大, 往往只可应用于较小的分子体系. 目前, 可用来计算大分子及生物体系的力场方法有AMBER[10], CHARMM[11], GROMOS[12]和OPLS[13]等.

近年来, 对于甲醇团簇体系及离子甲醇团簇体系的研究已较多[6,7,9,14～20]. Boyd等[6]采用密度泛函理论研究了(CH3OH)n(n=2～12)体系的势能面, 发现配位数相同的甲醇团簇中环状结构更稳定. Pires等[7]使用PM3, Hartree-Fock, B3LYP, MP2方法和ONIOM模型模拟了(CH3OH)n(n=2～12,16,20)体系的结构、结合能和振动频率等, 发现甲醇团簇的稳定性主要依靠氢键, 而环状结构具有最多的氢键, 与Boyd等[6]的结论一致. Kazachenko等[16]对(CH3OH)n(n≤15)体系进行了研究, 发现在甲醇的大分子结构中, O原子与C上H原子的弱相互作用也是维持分子稳定的关键. Morrone等[17]使用QM/MM方法针对甲醇体系建立模型, 即对羟基部分使用密度泛函理论, 对甲基部分使用AMBER力场, 测定了气相下甲醇单体、二聚体及甲醇溶液的结构, 得到与实验相符的结果. Zeng等[18]对Na+的甲醇溶液进行Car-Parrinello动力学模拟, 提出对于Na+离子在甲醇中的配位数约为4, 其四配位构型比Jorgensen等[19]提出的六配位、Forck等[20]提出的五或六配位构型更稳定. 对于极性很强的离子液体体系, 仍旧缺乏一种普适性的可极化力场, 发展精确模拟电解质溶液中离子性质的力场仍是一个挑战[21].

Yang等[22,23]在密度泛函理论和电负性均衡方法的基础上, 充分考虑到分子中的化学键和孤对电子的作用, 提出了原子-键电负性均衡浮动方法(ABEEMσπ), 并将该方法融合进分子力学, 建立了原子-键电负性均衡浮动电荷分子力场方法(ABEEMσπ/MM)[23～29], 初步应用于对水、多肽和蛋白质、核酸等体系的结构和性质的研究, 获得了优于传统力场的结果.

本文应用ABEEMσπ/MM方法和高水平量子化学计算方法, 对(CH3OH)n(n=3～12)及[Na(CH3OH)n]+(n=3～6)体系进行研究, 根据从头算的结果, 构建合适的ABEEMσπ/MM势能函数, 调试相关参数, 并利用该函数对上述体系结构、结合能及电荷分布等性质进行计算, 得到较好结果, 为进一步动力学模拟研究甲醇电解质水溶液体系奠定了基础.

1　计算方法和理论模型

从头算采用Gaussian 09程序[30]和GaussView 5.0[31]软件. 使用MP2/6-31++G(d,p)方法对(CH3OH)n(n=3～6)及[Na(CH3OH)n]+(n=3～6)体系进行结构的优化和频率计算, 得到复合物的稳定结构. 选用MP2/6-311++G(2d,2p)方法计算体系单点能, 并进行基组重叠误差的校正, 计算了体系的结合能.

对(CH3OH)n(n=3～6)甲醇团簇使用MP2/6-31++G(d,p)和B3LYP/6-31G(d)两种方法进行结构优化. 结果表明, 两种方法获得的结构非常相近, 具体结果见表S1(见本文支持信息). 对(CH3OH)n(n=7～12)体系, 选用MP2/6-311++G(2d,2p)//B3LYP/6-31G(d)方法进行计算.

采用HF/STO-3G方法对电荷进行了Mulliken布局分析. 研究发现, 高水平基组会部分高估其电荷布居结果[32～35], 所以在ABEEM模型中, 一般使用HF/STO-3G来计算分子的电荷分布.

在ABEEMσπ/MM下, 构建(CH3OH)n(n=3～6)及[Na(CH3OH)n]+(n=3～6)体系的势能函数:

(1)

式中:i和j代表相互作用的不同分子;a和b表示分子上的不同原子;a-b和g-h代表体系中形成的不同化学键;lp为孤对电子;I表示金属离子.E的第1项为配体分子内化学键的伸缩振动势能, 其中kr表示键长伸缩力常数,r为键长的真实值,req表示键长的平衡值; 第2项为键角的弯曲振动势能, 采用谐振子势函数来描述;fθ为键角弯曲力常数,θ表示键角的真实值,θeq表示键角的平衡值. 第3项为二面角扭曲振动势能,V1,V2及V3为二面角扭曲力常数,φ为二面角的实际值.E的第4项为分子间的相互作用能, 包括范德华和静电相互作用, 分别采用通常的Lennard-Jones 12-6形式和库仑定律来计算.εia,jb与σia,jb分别表示第i个分子中的原子a和第j个分子中的原子b之间的势阱深度和碰撞半径,qia,qi(a-b)及qi(lp)分别为第i个分子中各位点所带的电荷, 由ABEEMσπ/MM获得.

ABEEMσπ/MM模型的位点包括原子位点、化学键位点(σ位点和π位点)和孤对电子位点,σ键位点处于2个成键原子共价半径之比处;π键位点处于垂直于双键所在的平面, 置于双键原子上下两侧共价半径处; 孤对电子位点则处于距离原子共价半径处.Ria,jb,Ri(a-b),j(g-h),Ri(lp),j(lp′),Ria,j(g-h),Ria,j(g-h),Ria,j(lp)及Ri(a-b),j(lp)分别表示第i个与第j个分子中的各电荷位点(原子、键、孤对电子)之间的距离.k为整体协调因子, 其值为0.57.RiH,j(lp)表示氢原子与孤对电子的氢键相互作用区域的距离,klp,H(RiH,j(lp))表示RiH,j(lp)对应的氢键拟合函数.RI,i(lp)和kI,lp分别表示金属离子I和第i个CH3OH中O原子孤对电子的距离及它们之间的静电拟合函数. 其中, 氢键拟合函数及静电参数可以防止强烈作用的两个原子间电荷形成过度极化, 从而对维持复合物的稳定性起到重要作用.

为更好地描述体系中分子间氢键的相互作用, 引入氢键拟合函数k(R):

(2)

式中:A,B,C和D均为玻尔兹曼函数中的常数.

ABEEMσπ/MM参数可分为力场参数和电荷参数. 力场参数主要包括键长伸缩振动、键角弯曲振动和范德华相互作用等, 可看做硬自由度参数, 具有较好的可转移性, 可从其它力场和实验值借鉴. 电荷参数来自本文工作, 电荷参数列于表1和表2. 当体系参数发生变化时, 其对应的稳定结构会发生改变, 进而体系的电荷分布和结合能都要重新计算. 本文通过调节(CH3OH)n体系的价态电负性χ*, 价态硬度2η*、范德华参数(σ,ε)(表1)以及氢键拟合函数等相关参数(表2), 以(CH3OH)n(n=3～6)体系的从头算结果作为参考, 通过改变与优选体系的结构、电荷和结合能等性质, 使之与从头算所得结果一致, 以验证模型及参数的可靠性. 在对环状甲醇(CH3OH)n(n=3～6)体系取得较好结果的基础上, 对(CH3OH)n(n=7～12)体系进行计算, 验证模型及参数的可转移性. 同时, 在不改变已确定的甲醇体系相关参数的情况下, 通过调节Na+的相关电荷参数, 使Na+(CH3OH)n体系亦得到与从头算相符的结果.

Table 1ABEEMσπ/MM parameters(χ*, 2η*,σ,ε) of (CH3OH)nand Na+(CH3OH)n

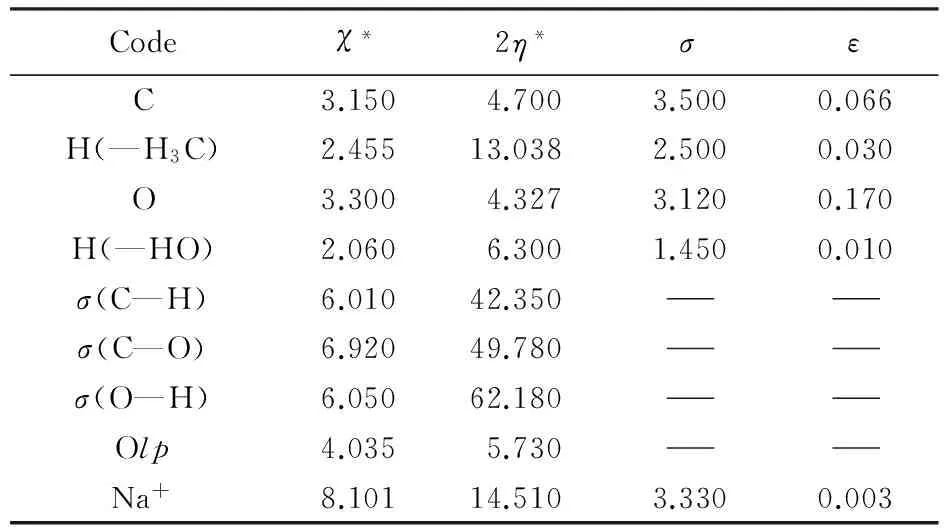
Codeχ*2η*σεC3.1504.7003.5000.066H(—H3C)2.45513.0382.5000.030O3.3004.3273.1200.170H(—HO)2.0606.3001.4500.010σ(C—H)6.01042.350σ(C—O)6.92049.780σ(O—H)6.05062.180Olp4.0355.730Na+8.10114.5103.3300.003

Table 2　Parameters of klp,H

2　结果与讨论

2.1(CH3OH)n(n=3～12)体系

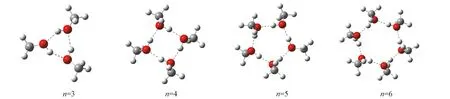
Fig.1　　　　Stable geometry of cyclic (CH3OH)n(n=3—6) optimized via ab initio and ABEEMσπ/MM

2.1.1(CH3OH)n(n=3～6)的几何结构计算结果表明, 对于相同大小的甲醇团簇, 相对于链状、带支链的环和带支链的链状结构, 环状甲醇团簇的结构最稳定, 这与Boyd等[6]和Pires等[7]的计算结果一致. 图1为从头算与ABEEMσπ/MM优化(CH3OH)n(n=3～6)得到的稳定环状结构图. 表3给出了(CH3OH)n(n=3～6)在从头算方法、ABEEMσπ/MM、OPLS/AA力场及ONIOM方法计算下得到的分子内O—H平均键长ROH、分子间氢键的平均键长RO…H、相邻甲醇分子的氧原子间平均距离RO…O及相邻分子间氢键的平均键角∠O1—H1—O2, AAD为键长的绝对平均偏差, RRMSD为键长、键角和结合能的相对均方根偏差. 与从头算相比, ABEEMσπ/MM计算所得RO…H的AAD为0.0030 nm,ROH的AAD为0.0036 nm,RO…O的AAD为0.0011 nm, ∠O1—H1—O2的AAD为0.20°. ABEEMσπ/MM计算得甲醇单体分子ROH为0.0946 nm, QM计算得甲醇单体分子ROH为0.0964 nm, ABEEMσπ/MM计算结果与实验值0.0945 nm[36]更接近. 与甲醇单体分子内ROH相比, 团簇中分子ROH均大于单体ROH, 说明由于分子间氢键的形成, 拉长了分子内O—H键. 随着甲醇团簇内分子数n的增加, 分子内ROH呈现增大趋势,RO…H与RO…O均逐渐减小, ∠O1—H1—O2逐渐增大, 表明分子内氢键数目增多, 氢键键长逐渐缩短, 氢键强度增大, 体系结合更强. 通过结果对比表明, 使用ABEEMσπ/MM计算所得结构与从头算基本吻合, 整体结果优于OPLS/AA力场及ONIOM方法.

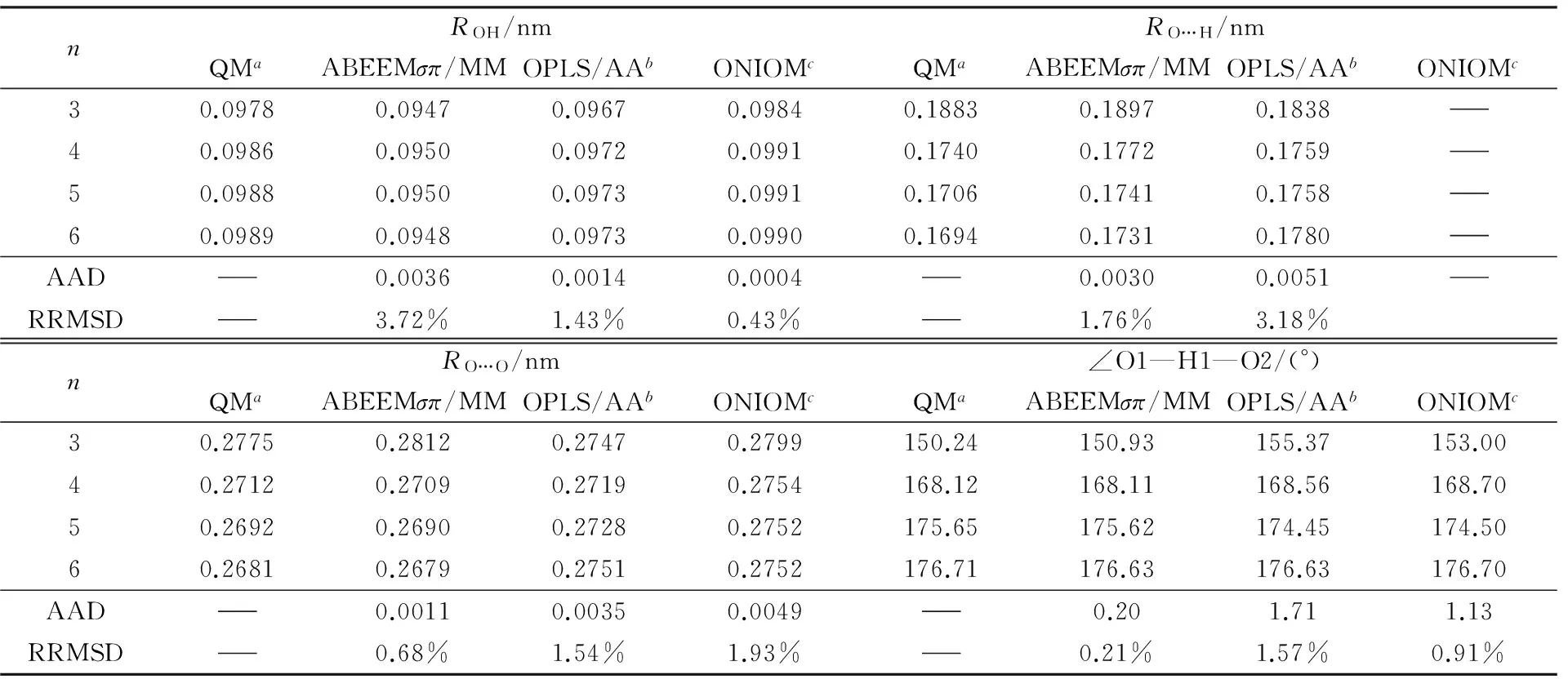
Table 3　　　　ROH, RO…H, RO…O and ∠O1—H1—O2 of cyclic (CH3OH)n(n=3—6)

a. MP2/6-31++G(d,p);b. this work;c. ref.[7].

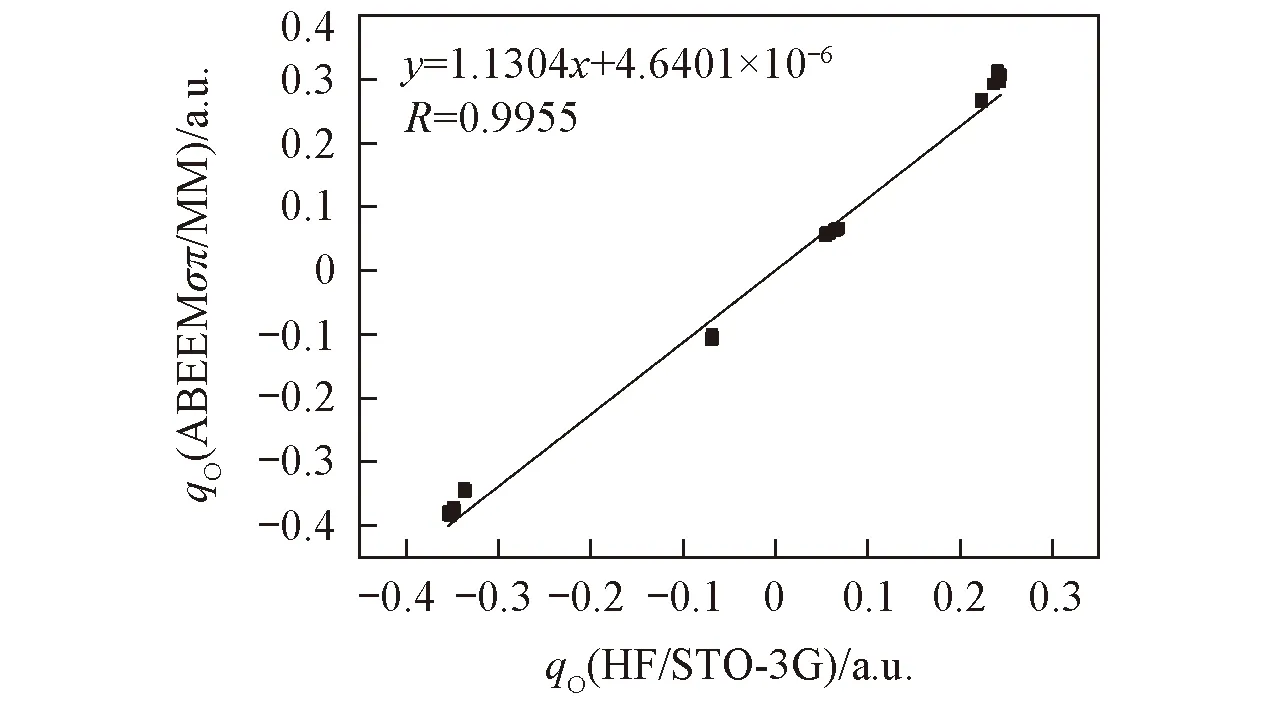
Fig.2　Charge linear correlation diagram of (CH3OH)n(n=3—6) via ab initio and ABEEMσπ/MM

2.1.2(CH3OH)n(n=3～6)的电荷分布图2为(CH3OH)n(n=3～6)体系总体的ABEEMσπ/MM和QM电荷线性相关图,R为方程线性相关系数. 可见ABEEMσπ/MM和QM方法计算结果的线性相关系数为0.9955, 线性相关方程的斜率接近于1, 截距均接近于0, 各个复合物的电荷分布的线性相关结果列于表S2(见本文支持信息). 可知对于各复合物, 标准偏差S不超过0.02, 最大偏差Umax<0.04, 2种方法计算氧原子位点电荷(qO)的AAD为0.0228 a.u., 说明2种方法具有极好的一致性. 且相比从头算方法, ABEEMσπ/MM能够更快速地计算出各原子位点、化学键及孤对电子上的电荷分布. 随着甲醇体系内分子数n由3增加到6, 分子间氢键数目的增多, 2种方法计算的O原子上电荷的绝对值均呈现增大趋势, O原子上电子密度增大, 氢键强度增大, 体系结合更紧密.

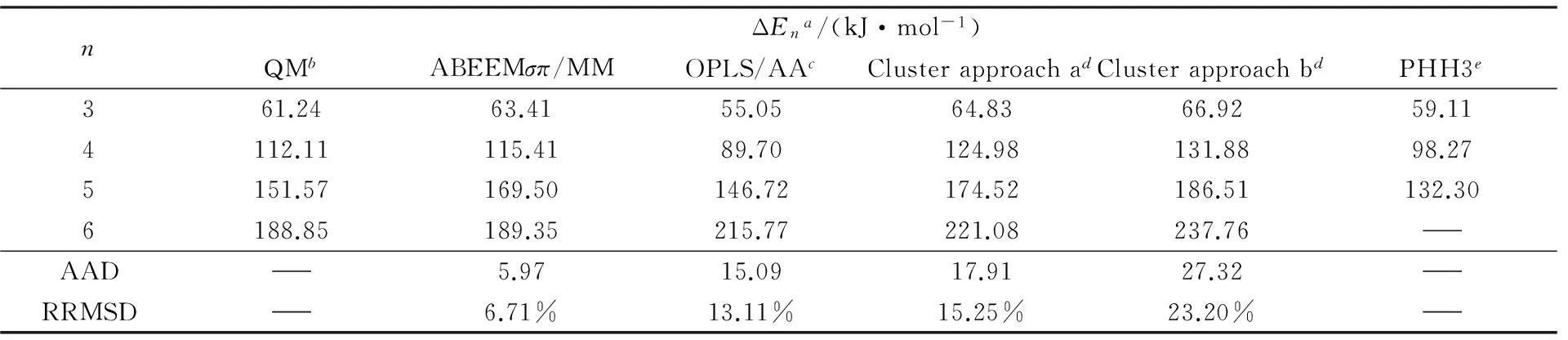
2.1.3(CH3OH)n(n=3～6)的结合能表4列出了应用QM方法、ABEEMσπ/MM、OPLS/AA力场、PHH3模型和2种cluster approach方法计算环状甲醇(CH3OH)n(n=3～6)体系最稳定结构的结合能. 由表4可见, 应用ABEEMσπ/MM构建的势能函数, 计算所得能量与MP2/6-311++(2d,2p)方法相比, 计算的绝对偏差在0.5～17.93 kJ/mol之间, 其AAD为5.97 kJ/mol, RRMSD为6.71%. 相较于OPLS/AA力场、PHH3及cluster approach方法, ABEEMσπ/MM与从头算的结果更接近. 随着分子数n的增加, 氢键数目增多, 几种方法计算所得的结合能均逐渐增大, 体系氢键强度增大, 结合更强, 具有一致性.

Table 4Binding energy(ΔEn) of cyclic methanol cluster(CH3OH)n(n=3—6) applied by MP2, ABEEMσπ/MM, OPLS/AA, PHH3 and cluster approaches

nΔEna/(kJ·mol-1)QMbABEEMσπ/MMOPLS/AAcClusterapproachadClusterapproachbdPHH3e361.2463.4155.0564.8366.9259.114112.11115.4189.70124.98131.8898.275151.57169.50146.72174.52186.51132.306188.85189.35215.77221.08237.76AAD5.9715.0917.9127.32RRMSD6.71%13.11%15.25%23.20%

a. ΔEn=nE(CH3OH)-E[(CH3OH)n];b. MP2/6-311++G(2d,2p);c. this work;d. ref.[37];e. ref.[38].

2.1.4模型及参数的验证为了验证模型及参数的合理性和可转移性, 将所调参数及势能函数应用于更大的甲醇团簇(CH3OH)n(n=7～12)体系, 计算其结构、结合能和电荷分布情况, 并与从头算及OPLS/AA力场结果进行对比, 结果列于表5～表7.

表5列出了(CH3OH)n(n=7～12)体系在使用QM方法及ABEEMσπ/MM、OPLS/AA力场下计算得到的分子内O—H平均键长ROH、分子间氢键的平均键长RO…H、相邻甲醇分子的氧原子间平均距离RO…O及相邻分子间氢键的平均键角∠O1—H1—O2. 表6为3种方法计算所得结合能的比较. 当n=12时, 使用OPLS/AA力场计算后团簇分散成多个小团簇及单体甲醇分子, 不能形成稳定的环状团簇结构, 因此无分子间氢键长、氢键角及结合能等数据. 从对比结果可见, ABEEMσπ/MM计算结果均明显优于OPLS/AA力场. 其中ABEEMσπ/MM计算距离的AAD不超过0.0008 nm, 键角的AAD为2.81°, 结合能的AAD为14.26 kJ/mol, RRMSD为5.08%. 表7为(CH3OH)n(n=7～12)体系的ABEEMσπ/MM和QM电荷分布的比较. 可见, 电荷的线性相关方程斜率接近于1, 截距接近于0, 线性相关系数R均大于0.99. 标准偏差S≤0.03, 最大偏差Umax<0.05, 2种方法计算O原子位点电荷的AAD为0.0066 a.u. 因此对于(CH3OH)n(n=7～12)体系, ABEEMσπ/MM力场仍与从头算方法具有较好的一致性, 可见, 本文调节的参数具有较好的可转移性.

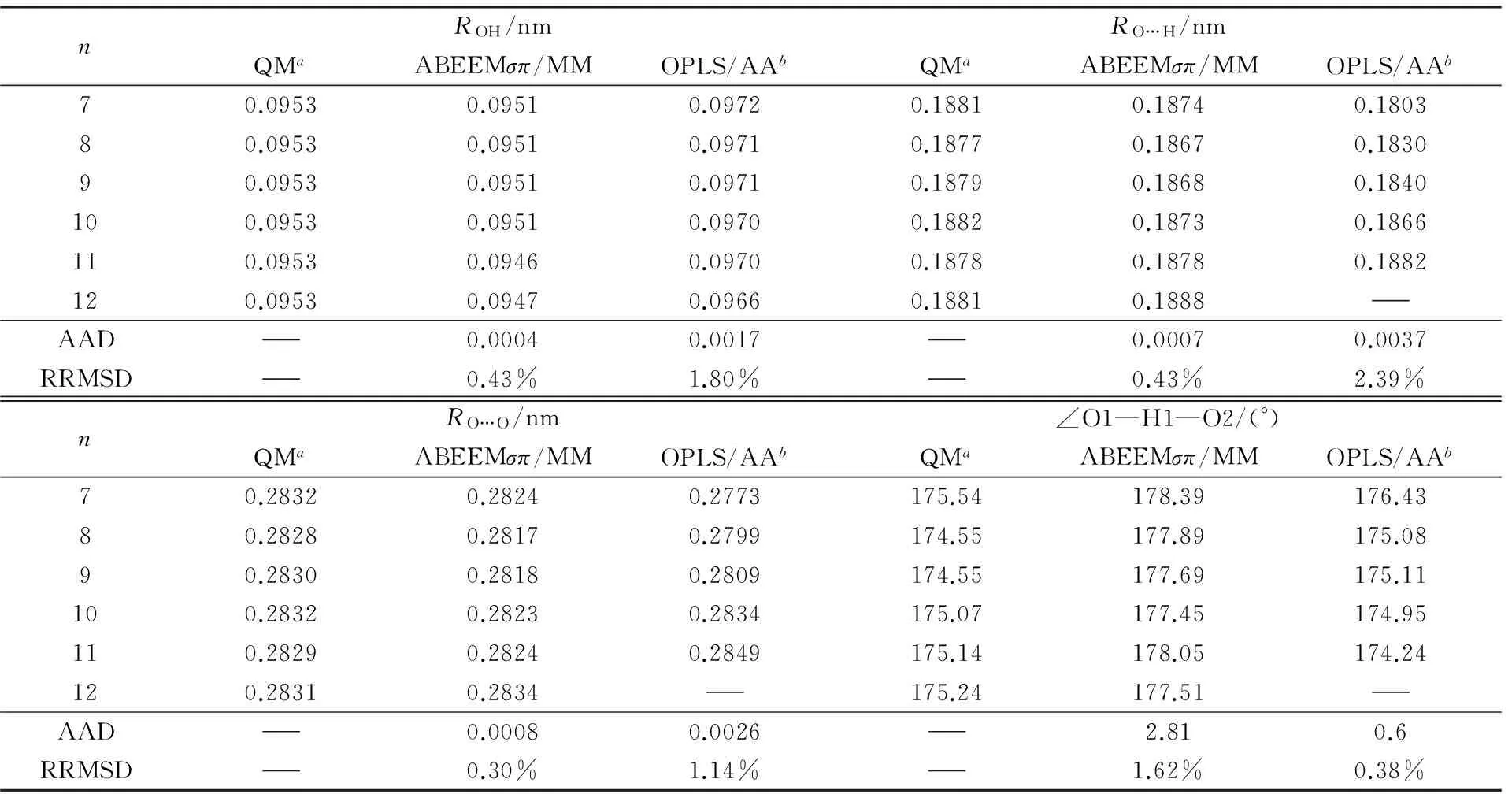
Table 5　ROH, RO…H, RO…O and ∠O1—H1—O2 of cyclic (CH3OH)n(n=7—12)

a. MP2/6-311++G(2d,2p)//B3LYP/6-31G(d);b. this work.

Table 6　ΔEn of cyclic (CH3OH)n(n=7—12)

a. ΔEn=nE(CH3OH)-E[(CH3OH)n];b. MP2/6-311++G(2d,2p)//B3LYP/6-31G(d);c. this work.

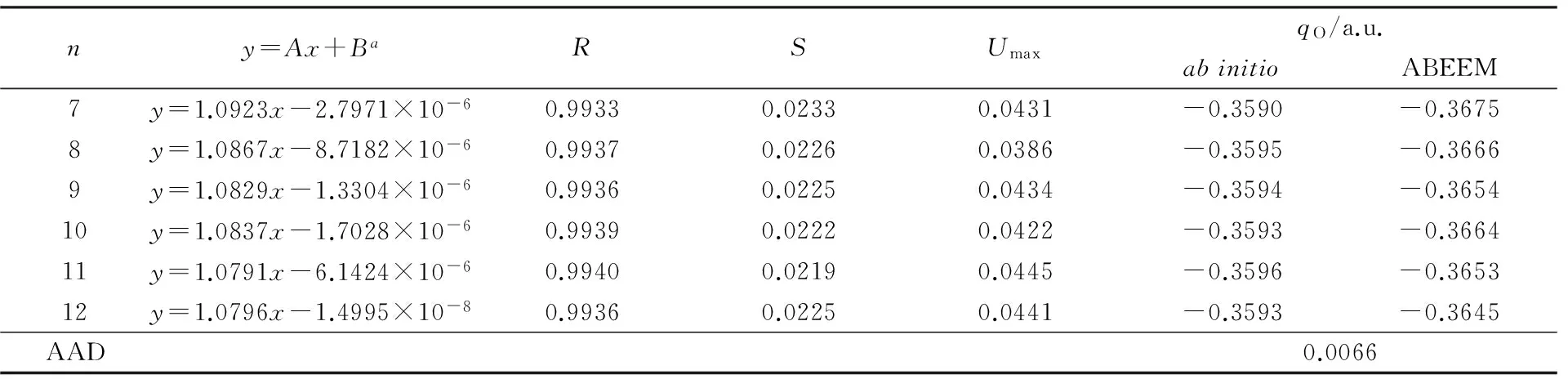
Table 7　Comparison of charge distributions for cyclic (CH3OH)n(n=7—12)*

*yis the charge calculated by ABEEMσπ/MM in linear correlation function;xis the Mulliken charge calculated by HF/STO-3G.

2.2[Na(CH3OH)n]+(n=3～6)体系

2.2.1[Na(CH3OH)n]+(n=3～6)的几何结构和结合能图3为使用从头算方法和ABEEMσπ/MM优化得到[Na(CH3OH)n]+(n=3～6)的稳定结构图, 由图3可见, Na+的第一溶剂层最多容纳4个甲醇分子, 即配位数为4, 当有更多甲醇分子出现, 则其排列在第二溶剂层, 这与Zeng等[18]的研究结果一致. 表8为对于[Na(CH3OH)n]+(n=3～6)体系分别使用从头算方法、ABEEMσπ/MM和OPLS/AA力场计算得到的Na+与O原子的平均距离RM…O、Na+与甲醇中O原子和C原子的平均键角∠M—O1—C1、相邻甲醇分子间平均氢键角∠O1—M—O2. 由表8可知, 随着分子中配位甲醇数目n的增加, 金属离子与内层分子间形成的RM…O略有减小, 金属离子与甲醇中氧原子的平均相互作用增强. ∠M—O1—C1逐渐增大, ∠O1—M—O2逐渐减小. ABEEMσπ/MM与从头算相比,RM…O的AAD为0.0024 nm, ∠M—O1—C1和∠O1—M—O2的AAD分别为1.48°和0.09°, 二者趋势一致, 且与从头算相比, ABEEMσπ/MM计算所得结果要显著优于OPLS/AA力场. 表8还给出了当n=3～6时, 使用3种方法计算的[Na(CH3OH)n]+体系的结合能ΔEn. 可见, 相对于从头算方法, 虽然ABEEMσπ/MM计算的相对平均偏差AAD为20.45 kJ/mol, RRMSD为6.58%, 但要明显优于OPLS/AA力场的结果.

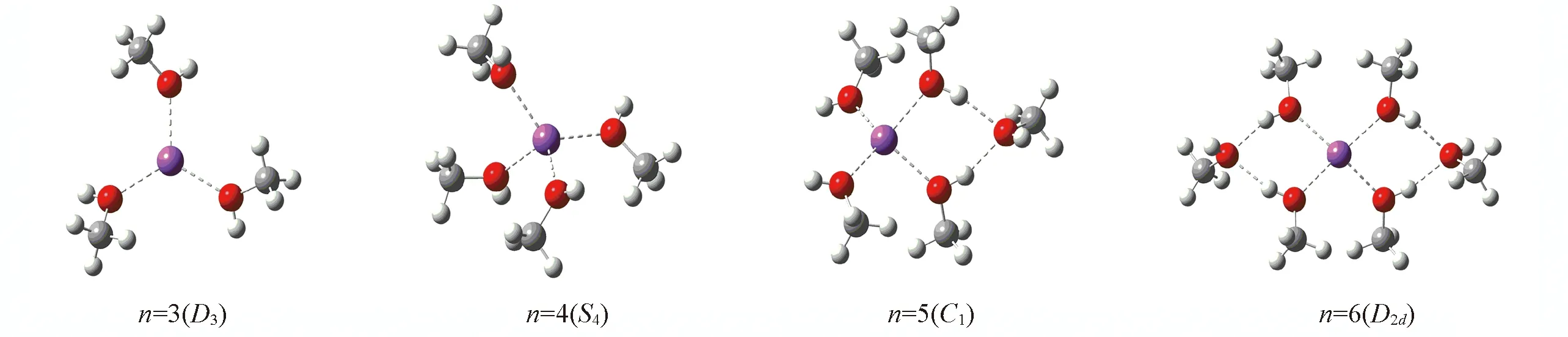
Fig.3　　　　Stable geometry of [Na(CH3OH)n]+(n=3—6) optimized via ab initio and ABEEMσπ/MM

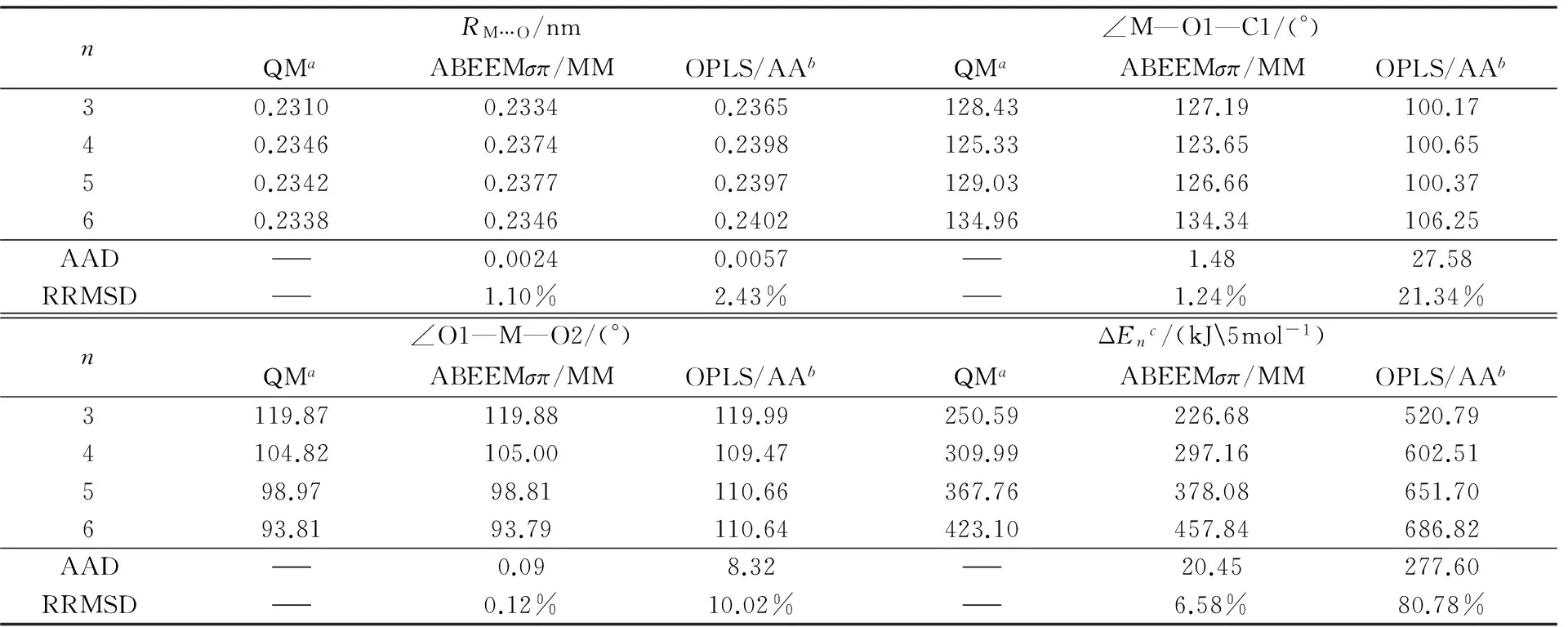
nRM…O/nm∠M—O1—C1/(°)QMaABEEMσπ/MMOPLS/AAbQMaABEEMσπ/MMOPLS/AAb30.23100.23340.2365128.43127.19100.1740.23460.23740.2398125.33123.65100.6550.23420.23770.2397129.03126.66100.3760.23380.23460.2402134.96134.34106.25AAD0.00240.00571.4827.58RRMSD1.10%2.43%1.24%21.34%n∠O1—M—O2/(°)ΔEnc/(kJ5mol-1)QMaABEEMσπ/MMOPLS/AAbQMaABEEMσπ/MMOPLS/AAb3119.87119.88119.99250.59226.68520.794104.82105.00109.47309.99297.16602.51598.9798.81110.66367.76378.08651.70693.8193.79110.64423.10457.84686.82AAD0.098.3220.45277.60RRMSD0.12%10.02%6.58%80.78%

a. MP2/6-31++G(d,p);b. this work;c. ΔEn=E[Na+] +nE[CH3OH] -E[(CH3OH)n].

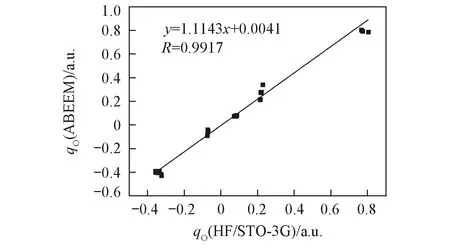
Fig.4　Charge linear correlation diagram of [Na(CH3OH)n]+(n=3—6) via ab initio and ABEEMσπ/MM

2.2.2[Na(CH3OH)n]+(n=3～6)的电荷分布图4为[Na(CH3OH)n]+(n=3～6)体系总体的ABEEMσπ/MM和QM电荷线性相关图. 由图4可见, ABEEMσπ/MM和QM获得电荷分布的线性相关方程斜率为1.1143, 线性相关系数为0.9917, 各个复合物的电荷分布的线性相关结果列于表S3(见本文支持信息). 可知对于各复合物, 标准偏差S接近于0.03, 最大偏差Umax不超过0.09, Na+离子电荷的绝对平均偏差为0.0241 a.u. 说明ABEEMσπ/MM能很好地应用于[Na(CH3OH)n]+(n=3～6)体系的电荷分布研究.

3　结　　论

采用从头算方法、ABEEMσπ/MM极化力场方法对环状醇簇(CH3OH)n(n=3～6)体系及[Na(CH3OH)n]+(n=3～6)体系构建了合适的势能函数, 通过调节价态电负性、价态硬度及氢键拟合函数等参数, 采用ABEEMσπ/MM计算得到能体系的结构、电荷分布和结合能与从头算结果一致, 与OPLS/AA力场计算结果进行对比. 结果表明, ABEEMσπ/MM极化力场方法的结果明显优于OPLS/AA力场. 相比于从头算, ABEEMσπ/MM获得键长的AAD<0.004 nm, 键长和键角的RRMSD分别小于3.8%和1.7%, 结合能的RRMSD<6.8%. ABEEMσπ/MM的电荷分布与从头算电荷分布的线性相关方程斜率接近于1, 截距接近于0, 线性相关系数均大于0.99. (CH3OH)n(n=7～12)体系的计算结果表明, ABEEMσπ/MM相关参数及势能函数可较好地应用于更大的团簇体系, 说明参数具有可转移性. 该结果为进一步将ABEEMσπ/MM极化力场方法推广应用于电解质溶液等复杂体系奠定了基础.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20160307.

[1]Mountain R. D.,Int.J.Thermophys., 2007, 28, 536—543

[2]Yizhak M.,Chem.Rev., 2009, 109, 1346—1370

[3]Jun S., Isao Y., Koji A.,Langmuir, 2010, 26, 8030—8035

[4]Medhekar N. V., Ramasubramaniam A., Ruoff R. S., Shenoy V. B.,ACSNano, 2010, 4, 2300—2306

[5]Marcus Y.,PureAppl.Chem., 2010, 82, 1889—1899

[6]Boyd S. L., Boyd R. J.,J.Chem.TheoryComput., 2007, 3, 54—61

[7]Pires M. M., de Turi V. F.,J.Chem.TheoryComput., 2007, 3, 1073—1082

[8]Reddy A. S., Sastry G. N.,J.Phys.Chem.A, 2005, 109, 8893—8903

[9]Rai D., Kulkarni A. D., Gejji S. P., Pathak R. K.,J.Chem.Phys., 2011, 135, 024307

[10]Ponder J. W., Case D. A.,Adv.ProteinChem., 2003, 66, 27—85

[11]Hart K., Foloppe N., Baker C. M., Denning E. J., Nilsson L., MacKerell A. D.,NewPhytologist, 2012, 8, 348—362

[12]Christen M., Hunenberger P. H., Bakowies D., Baron R., Bürgi R., Geerke D. P., Heinz T. N., Kastenholz M. A., Kräutler V., Oostenbrink C., Peter C., Trzesniak D., Gunsteren W. F. V.,J.Comput.Chem., 2005, 26, 1719—1751

[13]Kaminski G. A., Friesner R. A.,J.Phys.Chem.B, 2001, 105, 6474—6487

[14]Do H., Besley N. A.,J.Chem.Phys., 2012, 137, 134106

[15]Huang Z. G., Yu L., Dai Y. M.,Struct.Chem., 2010, 21, 565—572

[16]Kazachenko S., Bulusu S., Thakkar A. J.,J.Chem.Phys., 2013, 138, 224303

[17]Morrone J. A., Tuckerman M. E.,Chem.Phys.Lett., 2003, 370, 406—411

[18]Zeng Y. P., Hu J. M., Yuan Y., Zhang X. B., Ju S. G.,Chem.Phys.Lett., 2012, 538, 60—66

[19]Jorgensen W. L., Bigot B., Chandrasekhar J.,J.Am.Chem.Soc., 1982, 104, 4584—4591

[20]Forck R. M., Dauster I., Buck U., Zeuch T.,J.Phys.Chem.A, 2011, 115, 6068—6076

[21]Chen A. A., Pappu R. V.,J.Phys.Chem.B, 2007, 111, 11884—11887

[22]Yang Z. Z., Wang C. S.,J.Phys.Chem.A, 1997, 101, 6315—6321

[23]Yang Z. Z., Cui B. Q.,J.Chem.TheoryComput., 2007, 3, 1561—1568

[24]Yang Z. Z., Wu Y., Zhao D. X.,J.Chem.Phys., 2004, 120, 2541—2557

[25]Zhao D. X., Liu C., Wang F. F., Yu C. Y., Gong L. D., Liu S. B., Yang Z. Z.,J.Chem.TheoryComput., 2010, 6, 795—804

[26]Gong L. D.,Sci.ChinaChem., 2012, 55(12), 2471—2484

[27]Lu L. N., Liu C., Gong L. D.,Chem.Res.ChineseUniversities, 2013, 29(2), 344—350

[28]Liu L. L., Yang Z. Z.,Chem.J.ChineseUniversities, 2015, 36(11), 2179—2188

[29]Gong L. D., Ren W. H., Zhang Y. L., Li W. B., Yang Z. Z.,Sci.SinicaChim., 2016, 46, 114—125

[30]Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A.,etal.,Gaussian09,D.01, Gaussian Inc., Wallingford CT, 2013

[31]Dennington R., Keith T., Millam J.,GaussView,Version5, Semichem Inc., Shawnee Mission, KS, 2009

[32]Meher B. R., Kumar M. V. S., Bandyopadhyay P.,IndianJ.Phys., 2009, 83, 81—90

[33]Yang Z. Z., Cui B. Q.,J.Chem.TheoryComput., 2007, 3, 1561—1568

[34]Zhao D. X., Liu C., Wang F. F., Yu C. Y., Gong L. D., Liu S. B., Yang Z. Z.,J.Chem.TheoryComput., 2010, 6, 795—804

[35]Yang Z. Z., Wang J. J., Zhao D. X.,J.Comput.Chem., 2014, 35, 1690—1706

[36]Haynes W. M., Lide D. R.,CRCHandbookofChemistryandPhysics, 95thEdition, Boca Raton, CRC Press, 2014, 9—40

[37]Buck U., Siebers J. G.,J.Chem.Phys., 1998, 108, 20—32

[38]Hagemeister F. C., Gruenloh C. J., Zwier T. S.,J.Phys.Chem.A, 1998, 102, 82—94

(Ed.: Y, Z, S)

Studies of (CH3OH)n(n=3—12) and [Na(CH3OH)n]+(n=3—6)viaabinitioand ABEEMσπ/MM†

YU Yongbo, LIU Cui, GONG Lidong*

(SchoolofChemistryandChemicalEngineering,LiaoningNormalUniversity,Dalian116029,China)

The stable structures, charge distributions and binding energies of cyclic methanol cluster(CH3OH)n(n=3—12)and [Na(CH3OH)n]+(n=3—6) were studiedviaabinitioand the atom bond electronegativity equalization fluctuating charge force field(ABEEMσπ/MM). Based on theabinitioresults, the ABEEMσπ/MM fluctuating charge potential function were constructed and the related parameters were determined for the above systems. The results show that the structures, binding energies and other properties from ABEEMσπ/MM are in consistent with theabinitiocalculation, and better than the OPLS/AA force field. The average absolute deviation(AAD) of bond length is less than 0.004 nm, and the relative root mean square deviations(RRMSDs) of bond length, bond angle and binding energy are less than 3.8%, 1.7% and 6.8%, respectively. The linear correlation coefficients of the charge distributions of ABEEMσπ/MM andabinitiocalculation are all above 0.99.

† Supported by the National Natural Science Foundation of China(No.21133005), the Liaoning Excellent Talents in University(LNET) of China(No.LJQ2013111) and the Foundation of Liaoning Province Education Administration of China(No.L2014426).

Abinitio; ABEEMσπ/MM; Methanol; Sodium ion; Molecular interaction

2016-05-03. 网络出版日期: 2016-07-19.

国家自然科学基金(批准号: 21133005)、辽宁省高等学校优秀人才支持计划项目(批准号: LJQ2013111)和辽宁省教育厅一般项目(批准号: L2014426)资助.

O641

A

联系人简介: 宫利东, 男, 博士, 教授, 主要从事理论与计算化学研究. E-mail: gongjw@lnnu.edu.cn