多高层树状柱钢框架结构体系的抗震性能分析

张永咸，李启才，何若全

(苏州科技大学江苏省结构工程重点实验室， 江苏苏州215011)



多高层树状柱钢框架结构体系的抗震性能分析

张永咸，李启才，何若全

(苏州科技大学江苏省结构工程重点实验室， 江苏苏州215011)

为了进一步研究拼接节点削弱型树状柱钢框架结构体系的抗震性能，对代替钢梁拼接节点的三折线有限元计算模型进行改进，利用改进后的三折线模型设计了4层、6层、8层和10层按照拼接节点处实际内力值设计的树状柱平面钢框架。对上述4种结构模型输入地震波进行弹塑性时程分析，并与不设钢梁拼接节点的传统钢框架作比较分析。模拟结果表明，改进后的三折线模型更加接近真实情况，在不同地震波的作用下，按照实际内力设计拼接节点的树状柱钢框架与不设钢梁拼接节点的框架结构相比，其结构周期变大，最大基底剪力值显著减小，侧移值和层间侧移角也基本上都是减少，只有兰州波作用下10层结构由于高阶振型和共振等原因，使得侧移值和层间侧移角增大。

树状柱钢框架；时程分析；楼层侧移；层间侧移角；基底剪力

0　引　言

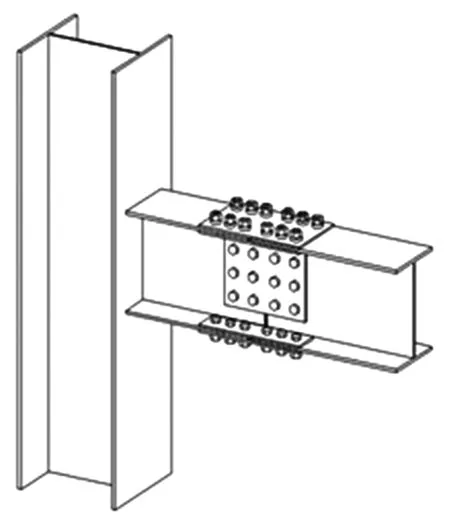
图1　树状柱钢框架连接节点Fig.1　Column-tree moment-resisting frame connection joint

传统刚性钢框架梁柱连接节点的焊缝大多数都在施工现场加工，难以保证其焊缝质量而易出现事故，如美国北岭地震中传统刚性钢框架梁柱焊缝处发生脆性破坏而引发坍塌[1-2]。为改进刚性钢框架的抗震性能，研究人员设计了钢梁高强螺栓拼接的树状柱钢框架。树状柱钢框架结构因形状类似树木的枝干而得名，其连接形式见图1。通过试验和有限元模拟研究表明，利用高强螺栓与拼接板之间、拼接板与拼接板之间的滑移以及高强螺栓杆与板件孔壁之间的挤压可以消耗地震能量，延缓梁柱焊缝处应力增加，提高钢框架抗震性能[3-5]。常鸿飞等[5-6]通过有限元分析发现，树状柱钢框架钢梁拼接节点的刚度和弹性强度有所削弱，但其极限承载力未减小，并认为拼接处不宜离梁端太远。改进的梁柱连接节点可以达到塑性铰外移的目的[7-11]。加强焊缝不能增加构件的延性，但利用高强螺栓滑移可以在地震作用下使钢梁拼接节点转动，起到塑性铰的作用，通过塑性铰的外移，达到保护梁柱焊缝的功能[12-13]。

王斌等[12]利用Sap2000有限元软件对文献[4]中的试验进行了模拟，用三折线模型代替试验中钢梁拼接部分，得到的模拟滞回曲线和试验滞回曲线吻合不错，证明了此方法的可用性。但是二者比较，已有的模拟曲线还是有明显不足，为此本文对三折线模型进行改进，并对文献[4]中的试验重新模拟。考虑到树状柱钢框架已有的研究主要集中在钢梁拼接节点处，不同层数树状柱结构的抗震性能的研究不是很多。因此，本研究建立不同层数的树状柱钢框架模型，并进行弹塑性时程分析，研究树状柱钢框架的抗震性能，为树状柱钢框架结构在实际工程中的使用提供参考。

1　连接节点的有限元模拟验证

1.1有限元模型修改

参考王斌等[12]模拟的方法和结果，对有限元模拟的模型做以下改进：①三折线模型中弯矩和刚度取值放大，具体数值见图3；②模拟模型中增加梁柱之间的加腋部分，由于Sap2000软件对构件过于简化，本文采用T型钢材代替试验的加腋部分，确保试验加腋部分的翼缘、腹板面积和T型钢材翼缘腹板面积相等，T型钢材的抗弯刚度和试验加腋部分的抗弯刚度一样。

1.2有限元模拟验证

在Sap2000有限元软件中建立模型，试验试件和有限元模型尺寸对比见图2。梁柱截面分别是H450 mm×160 mm×8 mm×16 mm和H350 mm×350 mm×10 mm×16 mm。 梁和柱的钢材材性参数值选用各自翼缘板材材性试验的数据。加腋处T型钢截面是T100 mm×100 mm×8 mm×16 mm，短梁与长梁之间的三折线模型采用MultiLinear Plastic连接单元，选用非线性强化滞回模型Kinematic。根据文献[13]中的公式，三折线模型中拼接处的滑移弯矩和极限弯矩采用M1=Mbs=182.13 kN·m及M3=Mu=352.08 kN·m 。对第二阶段的弯矩进行放大，取M2=1.3Mbs=236.77 kN·m。第一阶段弹性刚度K1=EI/L=45 200 kN·m，第二阶段和第三阶段分别是滑移和挤压阶段，拼接处的高强螺栓抗弯刚度仍然很大，对这两处的刚度根据试验情况进行放大，取K2=0.04K1=1 808 kN·m，K3=0.1K1=4 520 kN·m，正负方向对称，三折线理论模型见图3。

单位：mm

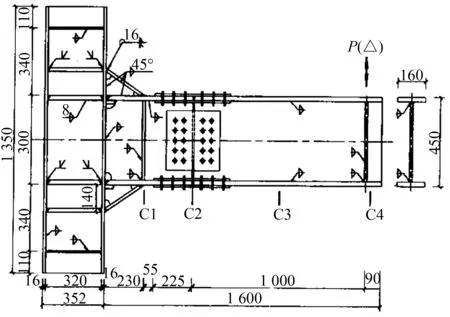
(a) 试验试件

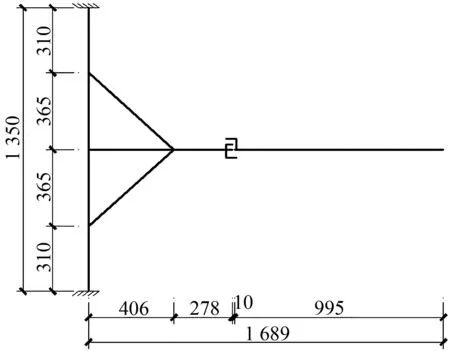
(b) 有限元模型

图2有限元模型和试验试件对比

Fig.2The compare of finite element simulation and test model

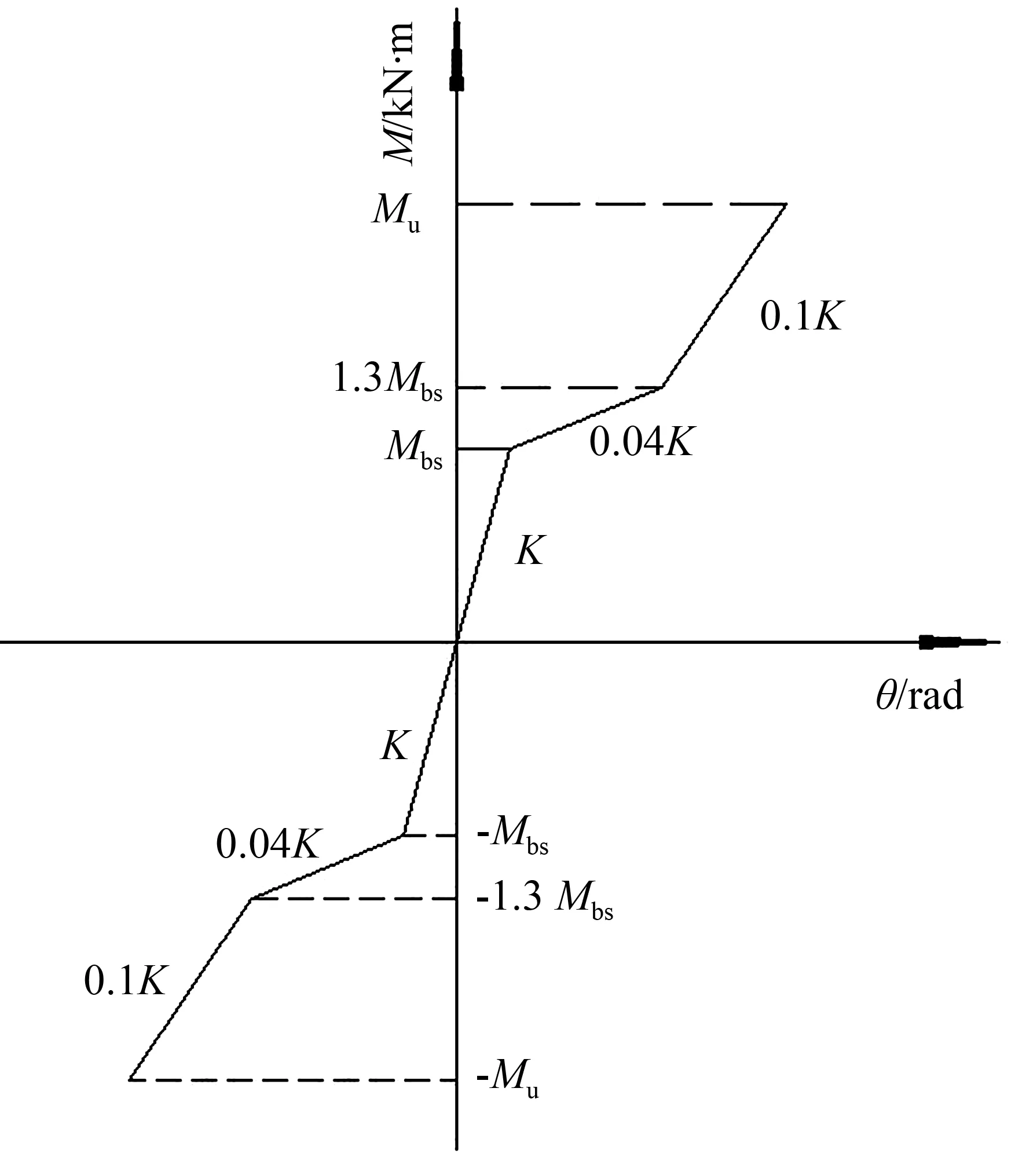
(a) 三折线理论模型

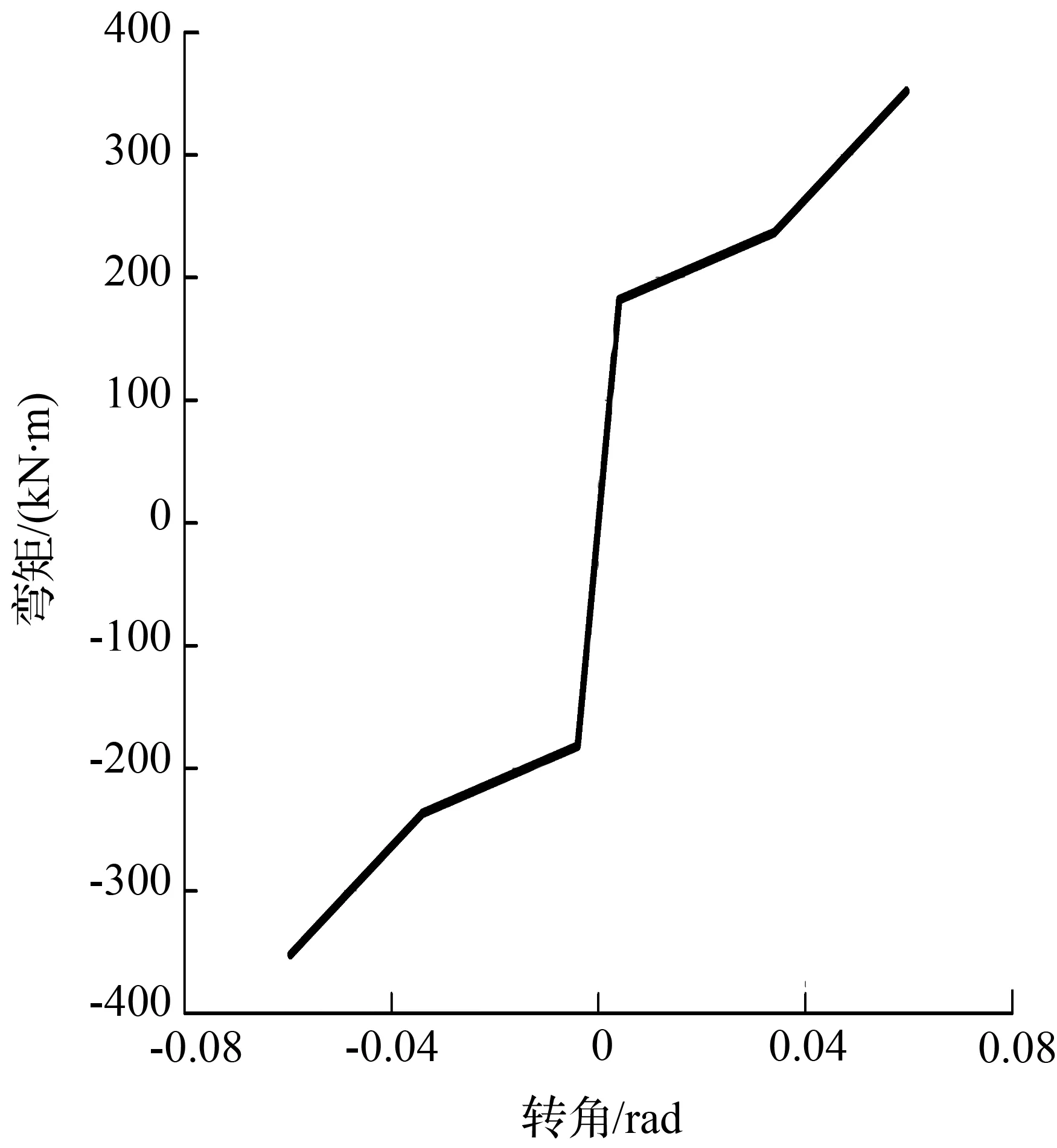
(b) 三折线数值模型

图3三折线理论模型

Fig.3The new-trilinear mode

在梁端部施加位移荷载，得到的滞回曲线与试验曲线对比见图4。从图4中看出,模拟滞回曲线最终承载力为372.544 kN，而试验负向承载力值为378 kN，两个最大荷载值达到98%左右；曲线进入第三强化阶段时拐点对应的侧移值也接近试验对应的侧移值。

不足之处：模拟曲线没有试验曲线饱满。主要原因：试验曲线的上升段是由于螺栓杆与孔壁的挤压导致构件承载力上升，与材料的包辛格效应无关；而模拟曲线中，由于短梁和长梁之间的三折线模型要遵循包辛格效应，所以当曲线进入第三强化阶段后，卸载反方向的加载点也跟着上升，导致整个曲线饱满程度差些。Sap2000软件的模型过于简化也是其中原因。

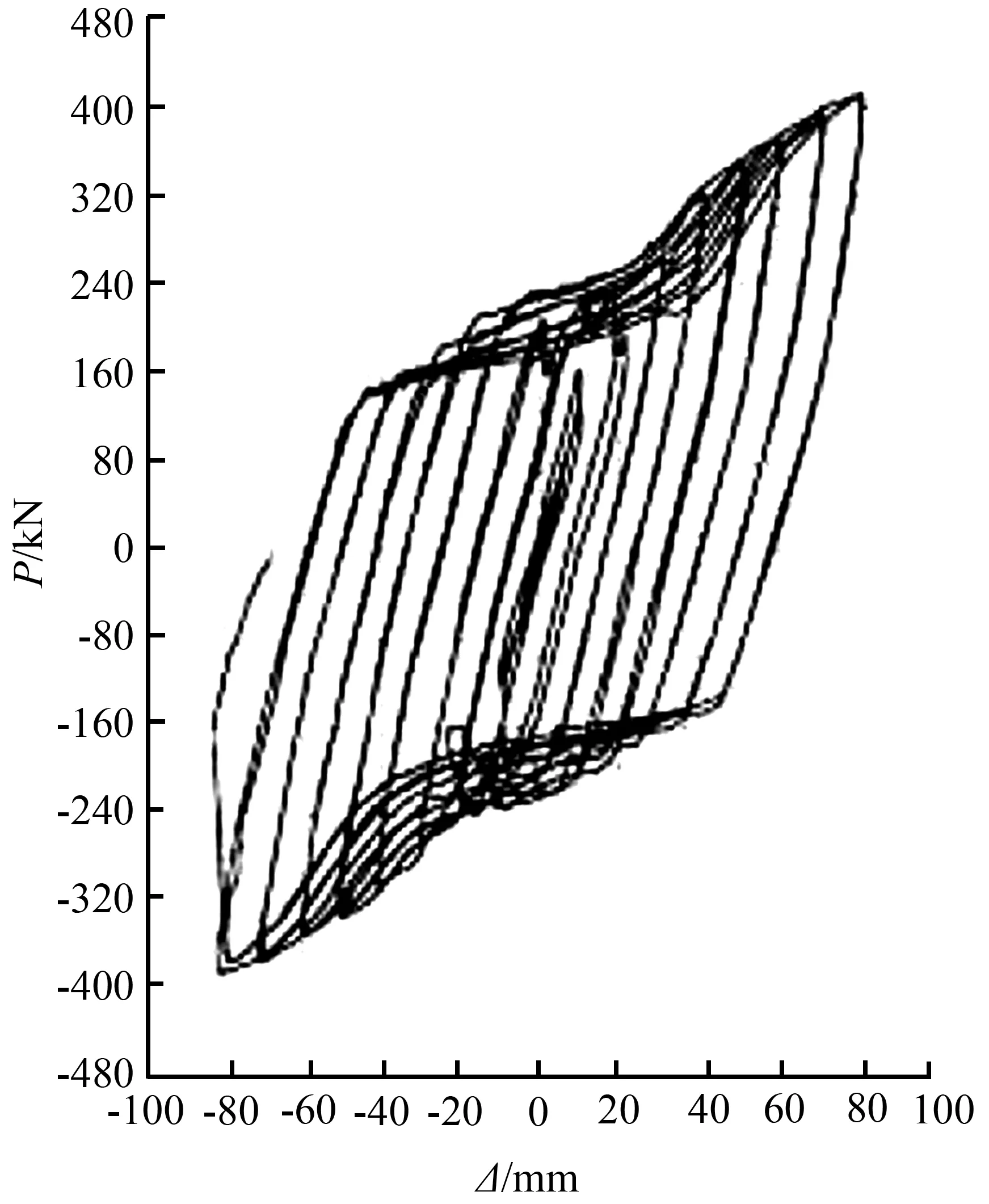
(a) 试验曲线

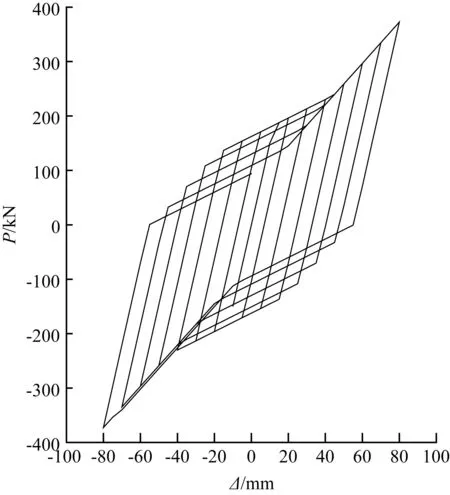
(b) 模拟曲线

图4模拟与试验滞回曲线对比

Fig.4Hysteresis curve comparison between simulation and test

2　有限元模拟

本研究设计的框架结构抗震设防烈度为8度(0.2g)，Ⅱ类场地，地震分组为第一组。设计层数分别是4层、6层、8层和10层的钢框架三维结构，取其中的单榀双跨做有限元分析。有限元模型分别建立传统刚性钢框架和树状柱刚性钢框架，共8个有限元模型，考虑装饰荷载，楼面厚度100 mm，恒载标准值4.0 kN/m2，活载标准值2.5 kN/m2。梁柱截面尺寸见表1，高强螺栓拼接中心线距离柱翼缘表面0.4 m，层高均是3.6 m，跨度均为7 m，选用Q345B钢材。

表1　模型各层梁柱截面尺寸Tab.1　Cross sectional dimension of model beams and columns

在Sap2000软件中，按照正常使用的设计方法，建立上述4种楼层的传统刚性钢框架，计算出离柱翼缘表面0.4 m处梁的实际弯矩和剪力值。取实际内力值作为设计值，设计树状柱钢框架模型钢梁拼接处高强螺栓的分布。不同楼层树状柱钢框架中各层梁的实际内力值不同，取数值相近楼层为同一区域，一共分为三组，记为节点1、节点2和节点3，高强螺栓节点在楼层中具体分布情况见表1。根据文献[13]中公式计算高强螺栓的个数。选用8.8级M20高强螺栓，抗滑移系数μ=0.3，拼接板厚度取10 mm，三组拼接节点如图5所示。根据高强螺栓的分布情况计算出钢梁拼接处的滑移弯矩Mbs、极限弯矩Mu和弹性刚度K1，按照图3(a)修改后的新三折线理论模型，建立各树状柱钢框架的三折线模型，具体数值见表2。

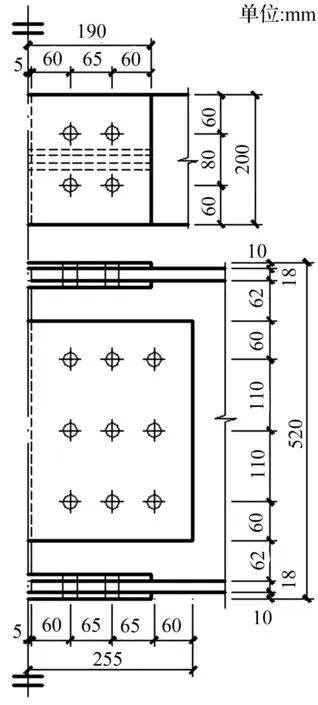
(a) 节点1螺栓分布

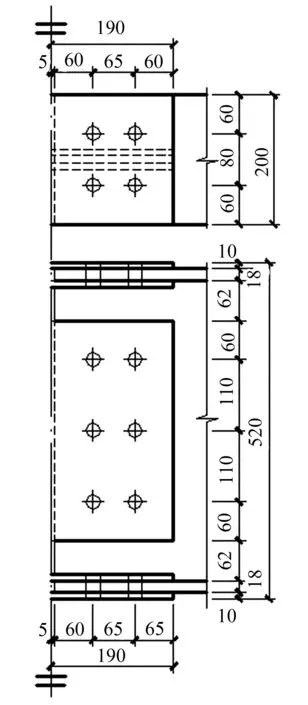
(b) 节点2螺栓分布

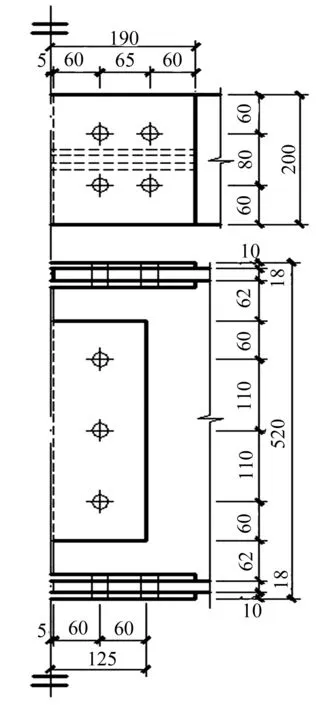
(c) 节点3螺栓分布

图5树状柱钢框架模型的高强螺栓分布

Fig.5Distribution of high-strength bolts in column-tree moment-resisting frame

表2高强螺栓节点参数值

Tab.2Parameter value of high-strength bolts

节点类别刚度K/(kN·m)刚度0.04K/(kN·m)刚度0.1K/(kN·m)Mbs/(kN·m)1.3Mbs/(kN·m)Mu/(kN·m)节点11.04×1054.15×1031.04×104174.7227.1568.4节点21.04×1054.15×1031.04×104159.8207.8548.96节点31.04×1054.15×1031.04×104145.0188.5529.6

3　地震作用下性能分析

选用El Centro波、迁安波和兰州波，调整加速度峰值满足8度(0.2 g)的大震抗震要求，地震波峰值为400 cm/s2，持续时间分别取30 s、22 s和17 s。

3.1结构顶层侧移和各层侧移分析

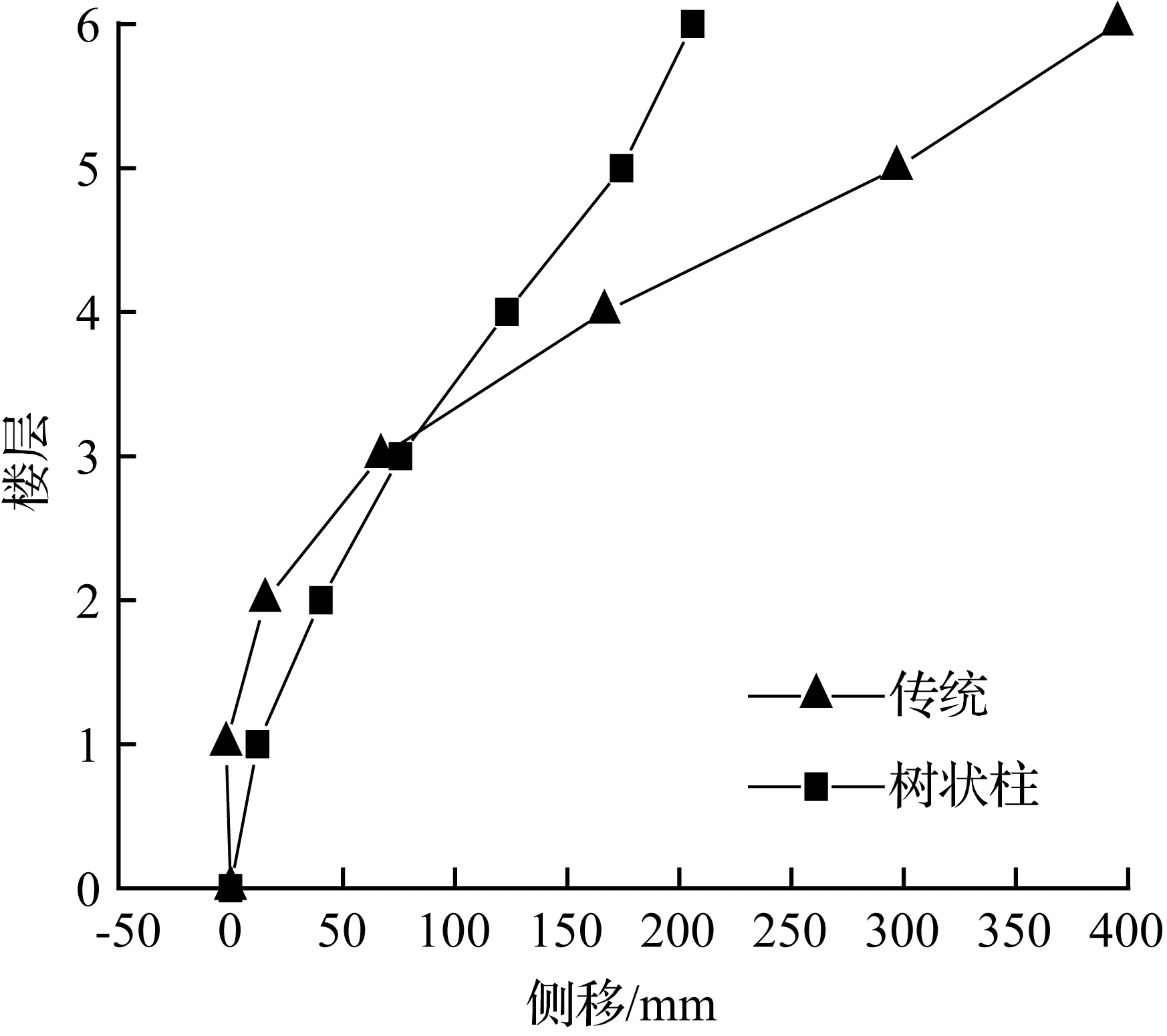
地震作用下模型的侧移曲线见图6～图8。树状柱钢框架顶点最大侧移值小于传统钢框架顶点最大侧移值，具体减小比例数值见表3。从表3中可看出，树状柱钢框架侧移的减小量最大达到63.0%，最小减小量也有16.6%。只有兰州波作用下的10层模型变化规律不一样，此处树状柱钢框架顶点侧移值增大53.0%，由于10层树状柱结构模型受高阶振型和周期影响，与兰州波产生共振，使得侧移增大。

表3　树状柱钢框架和传统钢框架的顶层侧移及减小比例Tab.3　The reducing ratio and top story drift between column-tree moment-resisting frames and the traditional steel frame

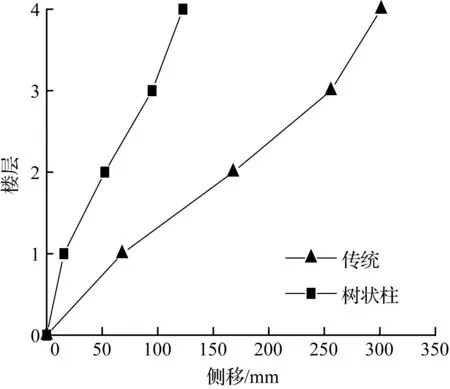
(a) 4层模型

(b) 6层模型

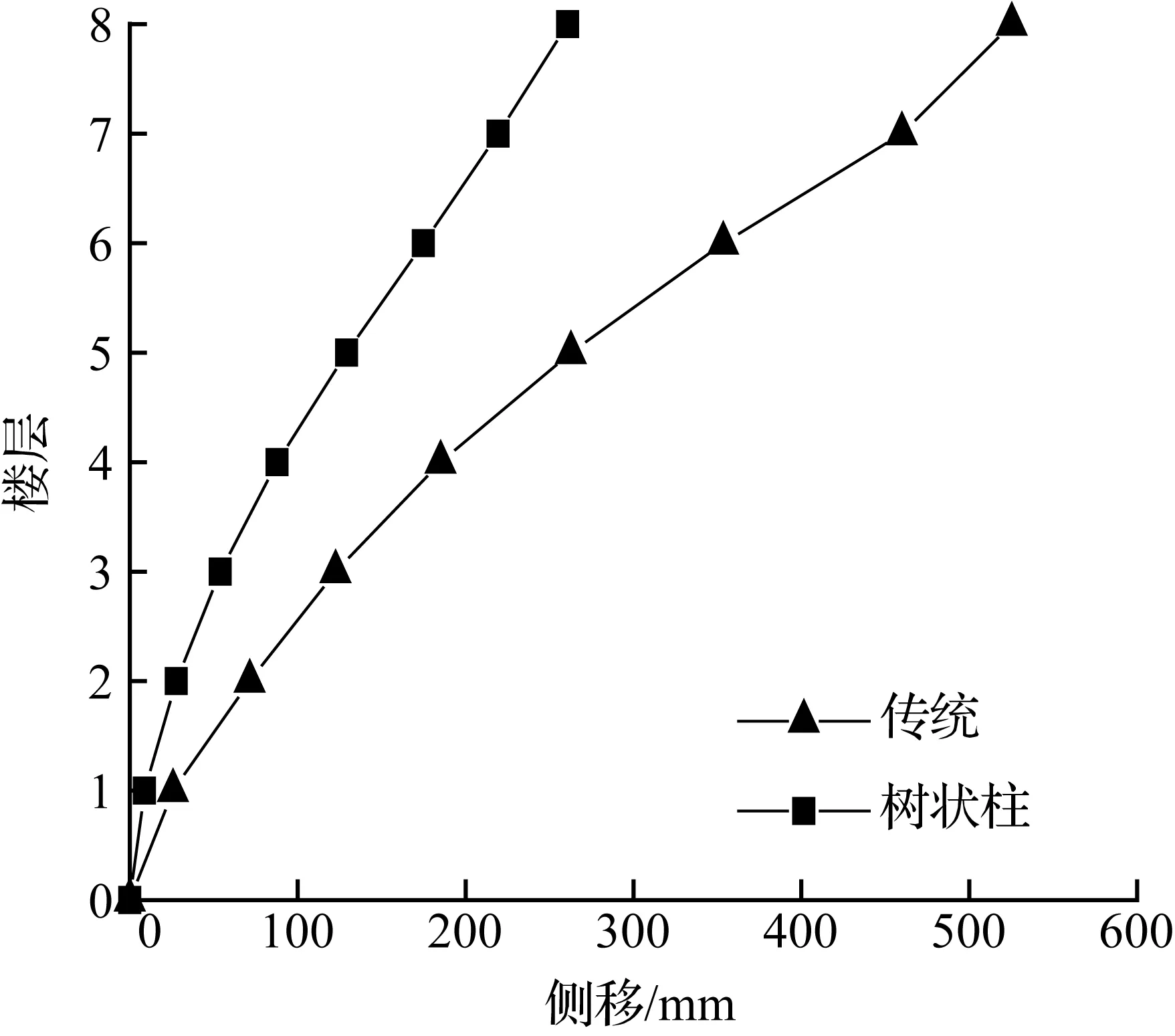
(c) 8层模型

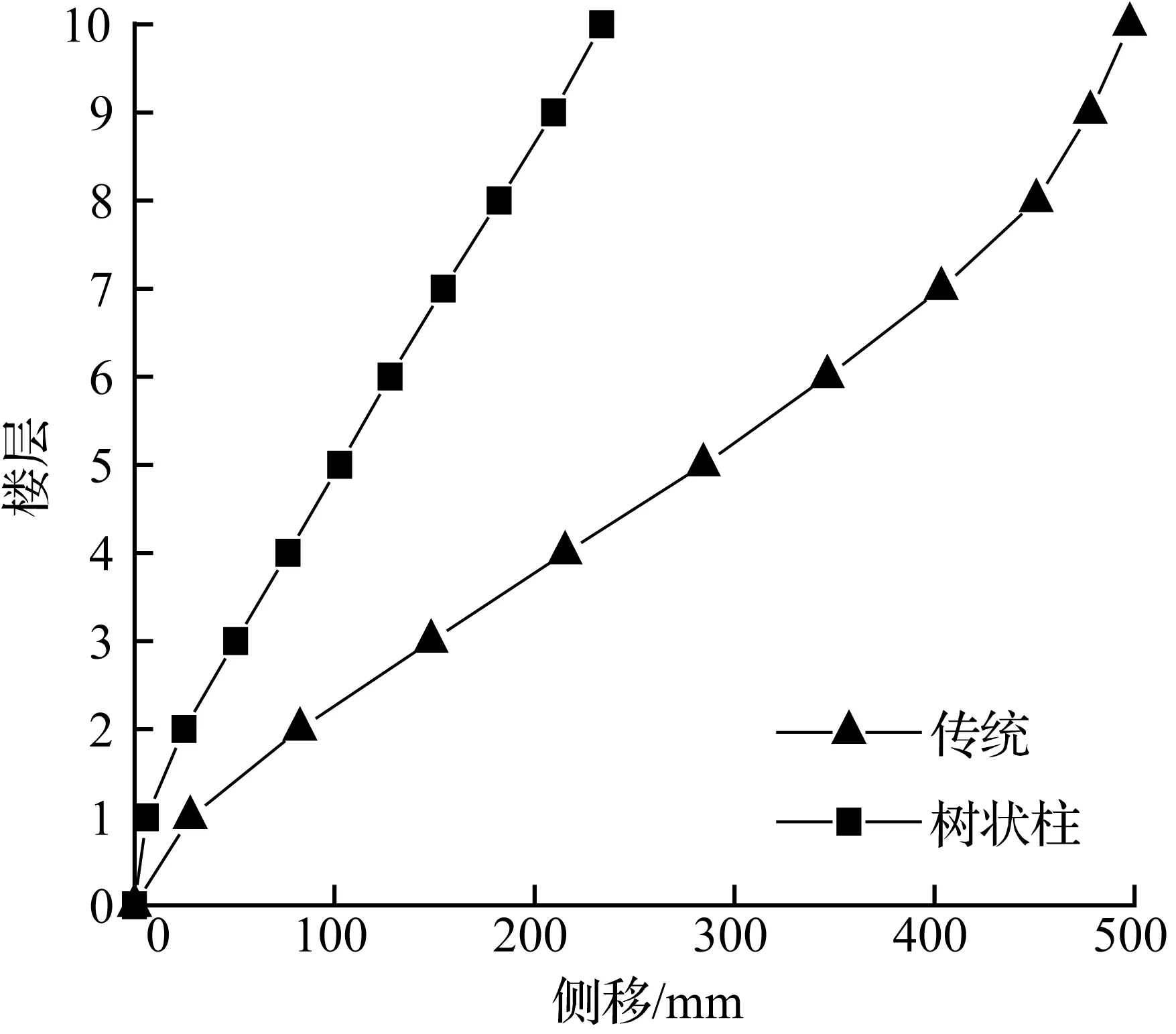
(d) 10层模型

图6El Centro波模型顶层侧移最大时刻各层侧移

Fig.6Drift of each story at the max drift of the top story for models in El Centro earthquake

(a) 4层模型

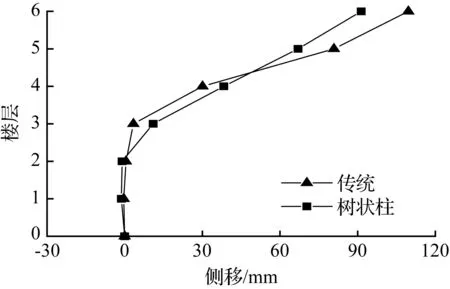
(b) 6层模型

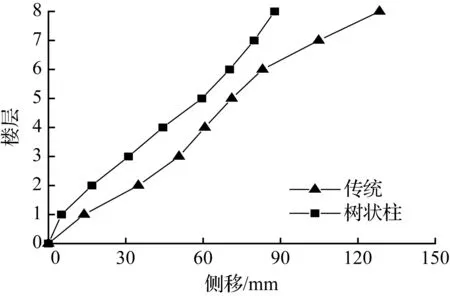
(c) 8层模型

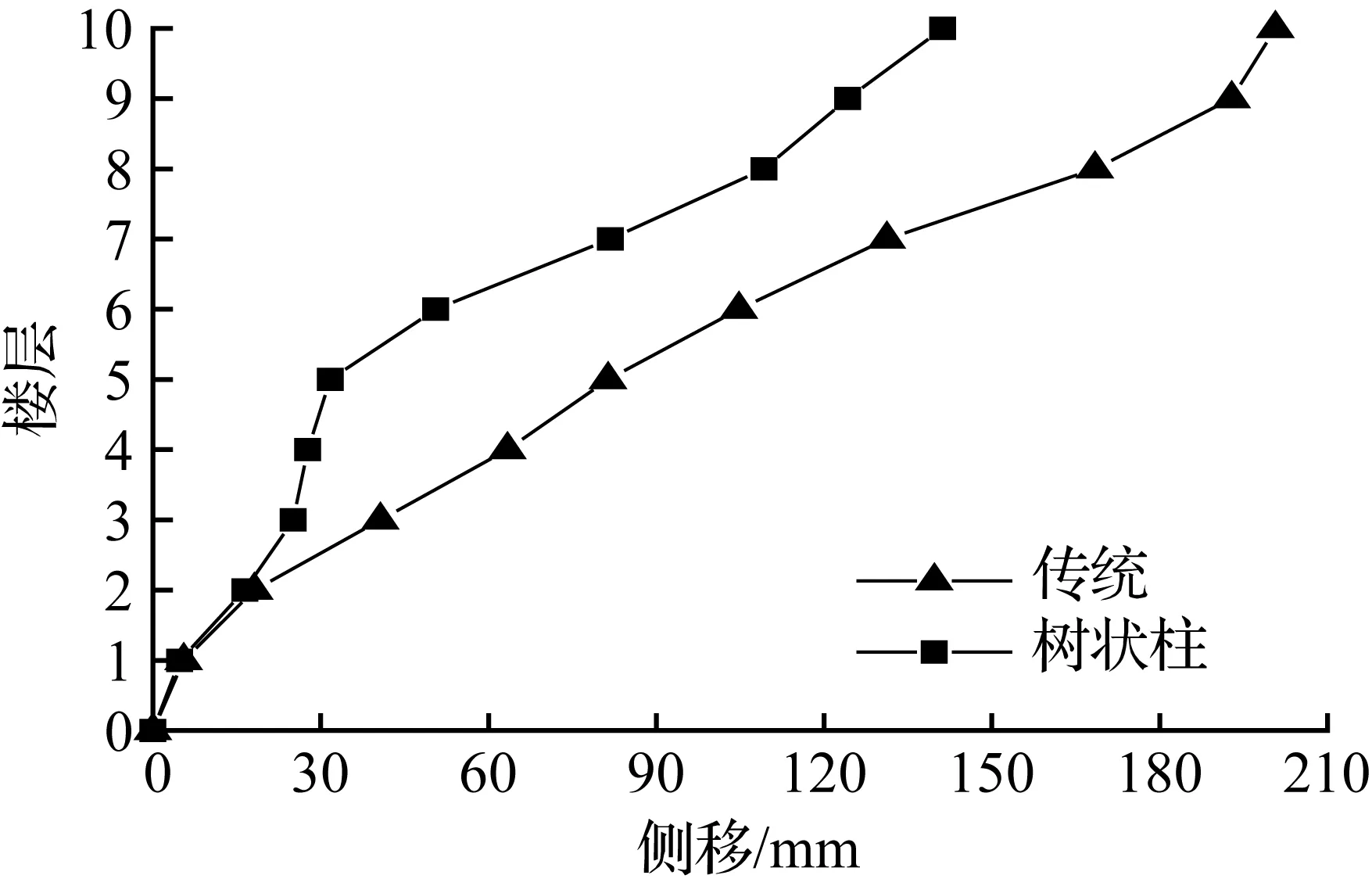
(d) 10层模型

图7迁安波各模型顶层侧移最大时刻各层侧移

Fig.7Drift of each story at the max drift of the top story for models in qianan earthquake

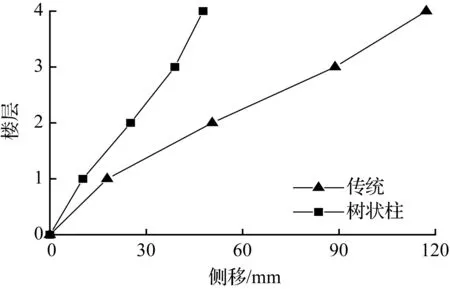
(a) 4层模型

(b) 6层模型

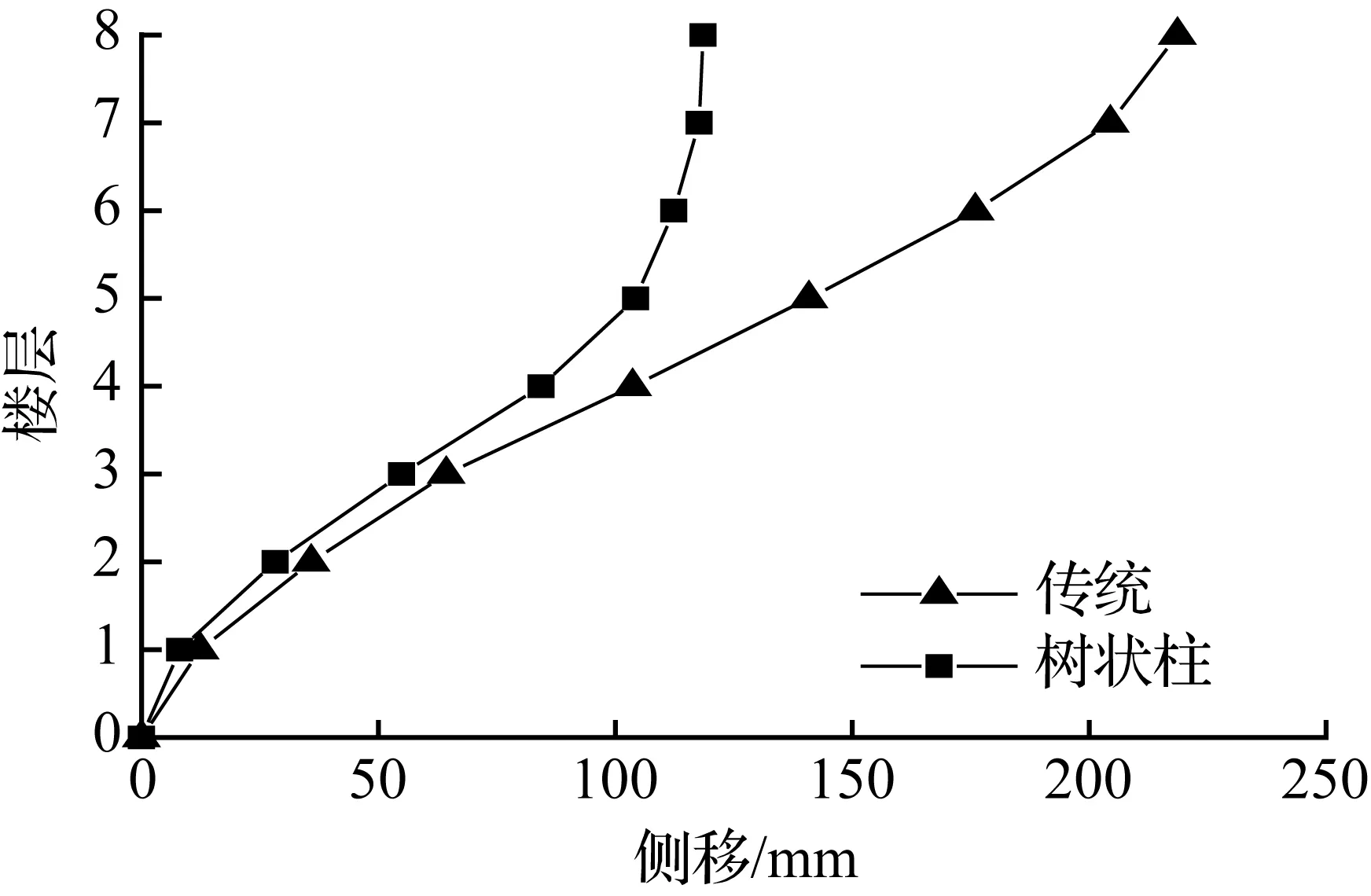
(c) 8层模型

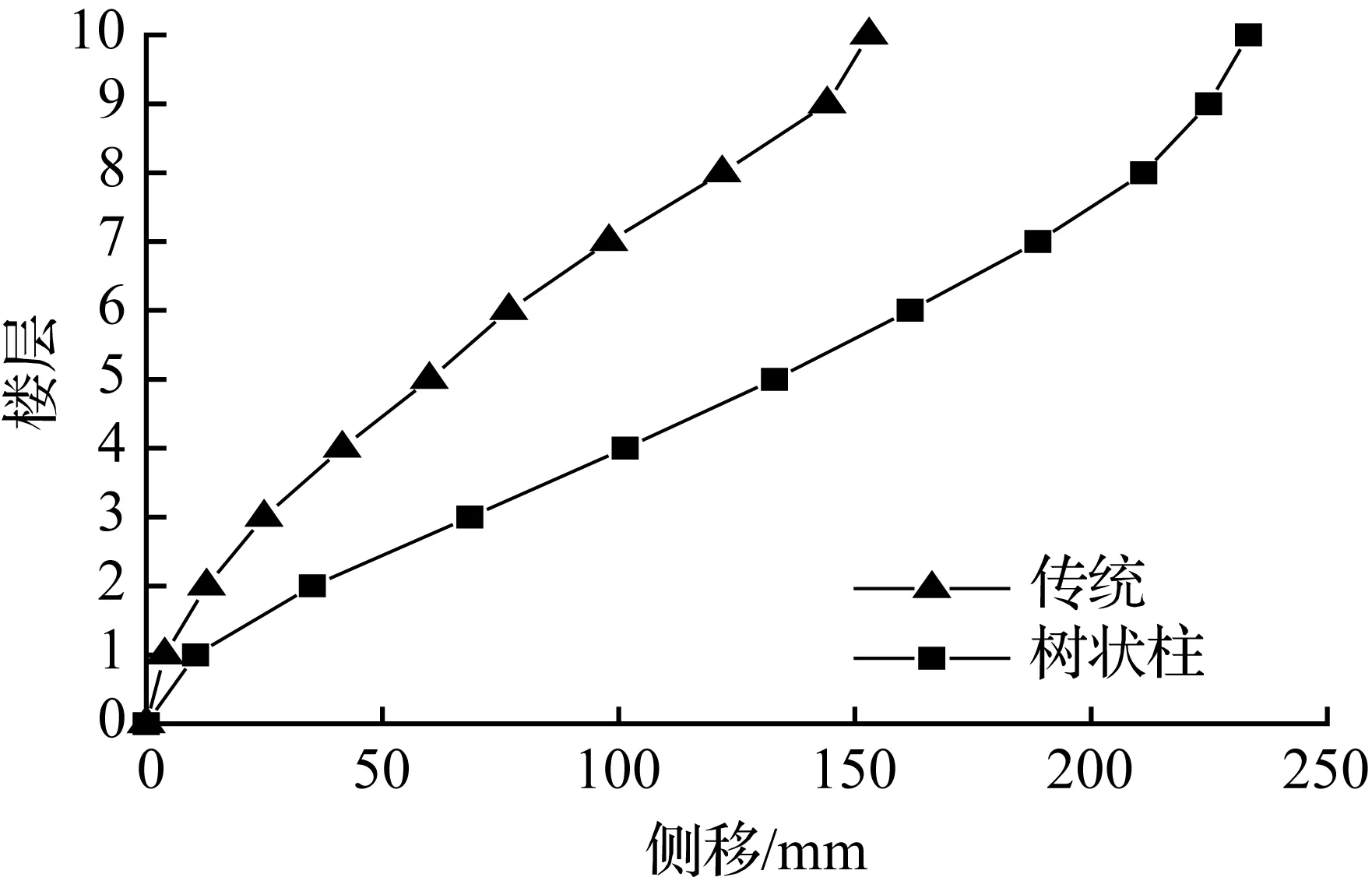
(d) 10层模型

图8兰州波各模型顶层侧移最大时刻各层侧移

Fig.8Drift of each story at the max drift of the top story for models in lanzhou earthquake

3.2层间侧移角分析

在地震波作用下，各模型的层间侧移角值曲线见图9～图11。从图中看出，树状柱钢框架相邻楼层间侧移角的变化量小于传统钢框架相邻楼层间的变化量，变化幅度更加缓和，稳定性能更好。

树状柱钢框架和传统钢框架模型层间侧移角最大值及减小比例见表4。从表4中可看出，树状柱钢框架的层间侧移角都没有超过我国现行《抗震设计规范》5.5.5规定的1/50限值，树状柱钢框架是安全可靠的。在低层和多层结构中，树状柱钢框架的层间侧移角小于传统钢框架的，但在兰州波作用下的10层结构中，树状柱钢框架层间侧移角增大38.8%，这和顶点侧移相对应。

表4　树状柱钢框架和传统钢框架的最大侧移角值及减小比例Tab.4　The reducing ratio and top story drift between column-tree moment-resisting frames and the traditional steel frame

(a) 4层模型

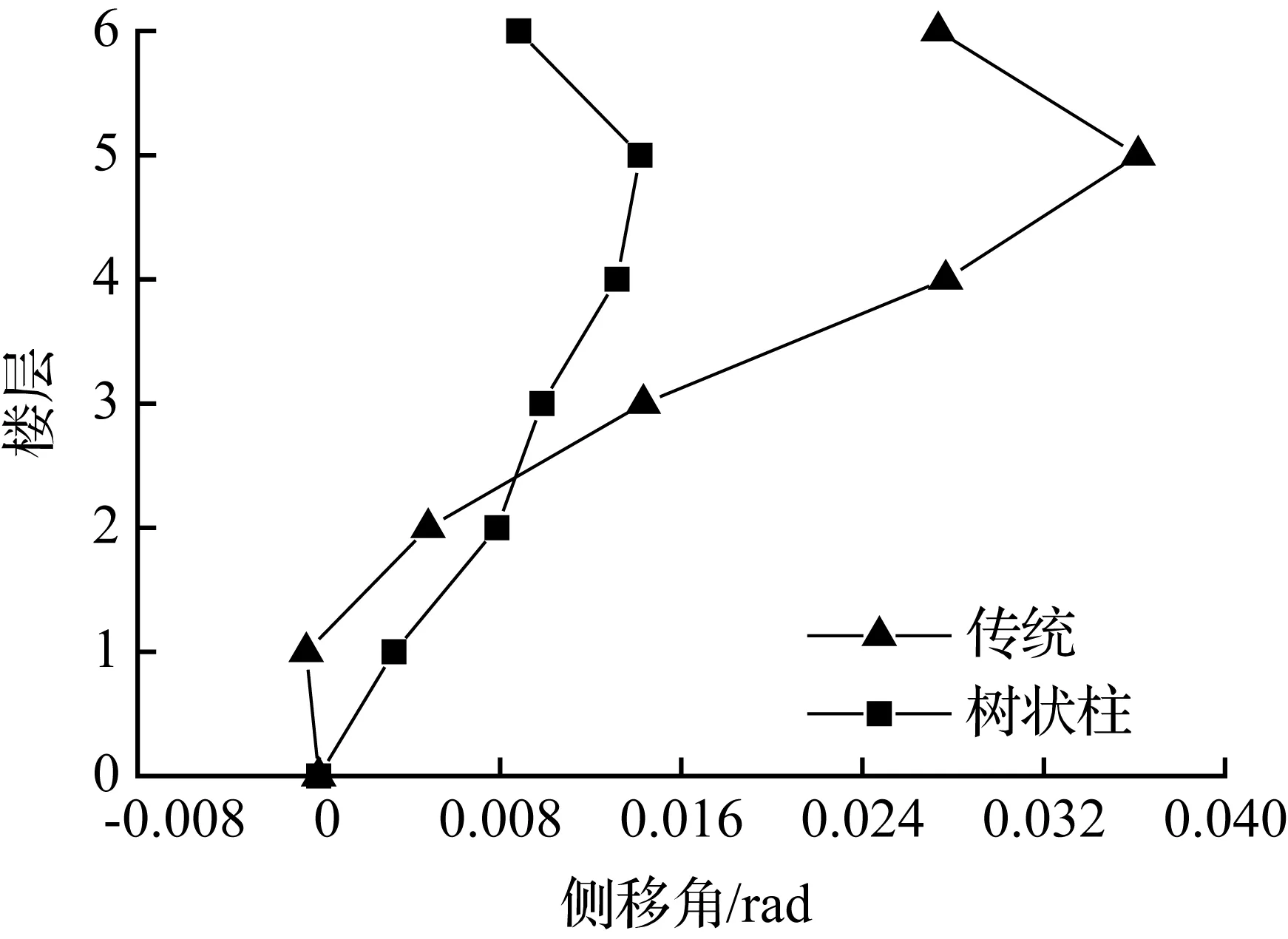
(b) 6层模型

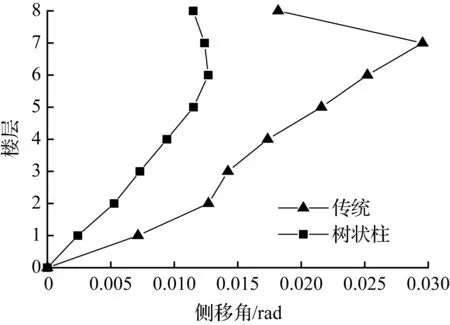
(c) 8层模型

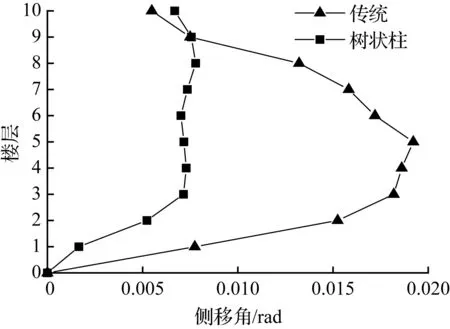
(d) 10层模型

图9El Centro波各模型顶层侧移最大时刻各层侧移角

Fig.9Story drift ratio of each story at the max drift of the top story for models in El Centro earthquake

(a) 4层模型

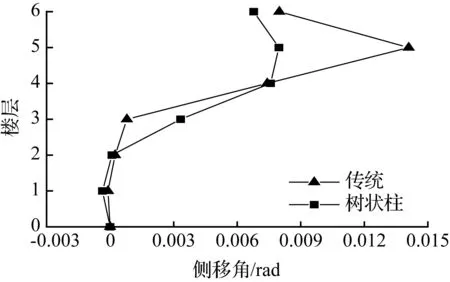
(b) 6层模型

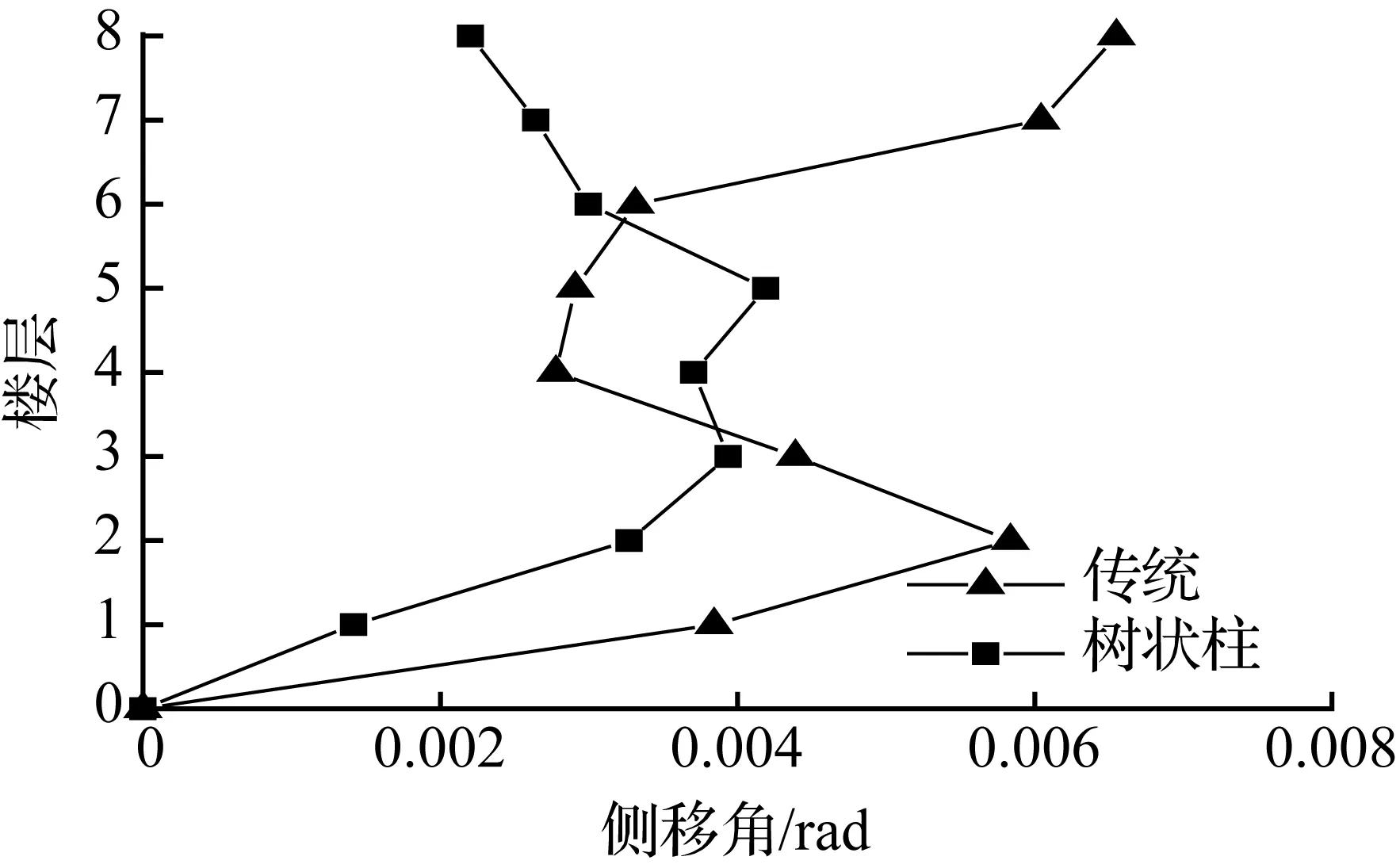
(c) 8层模型

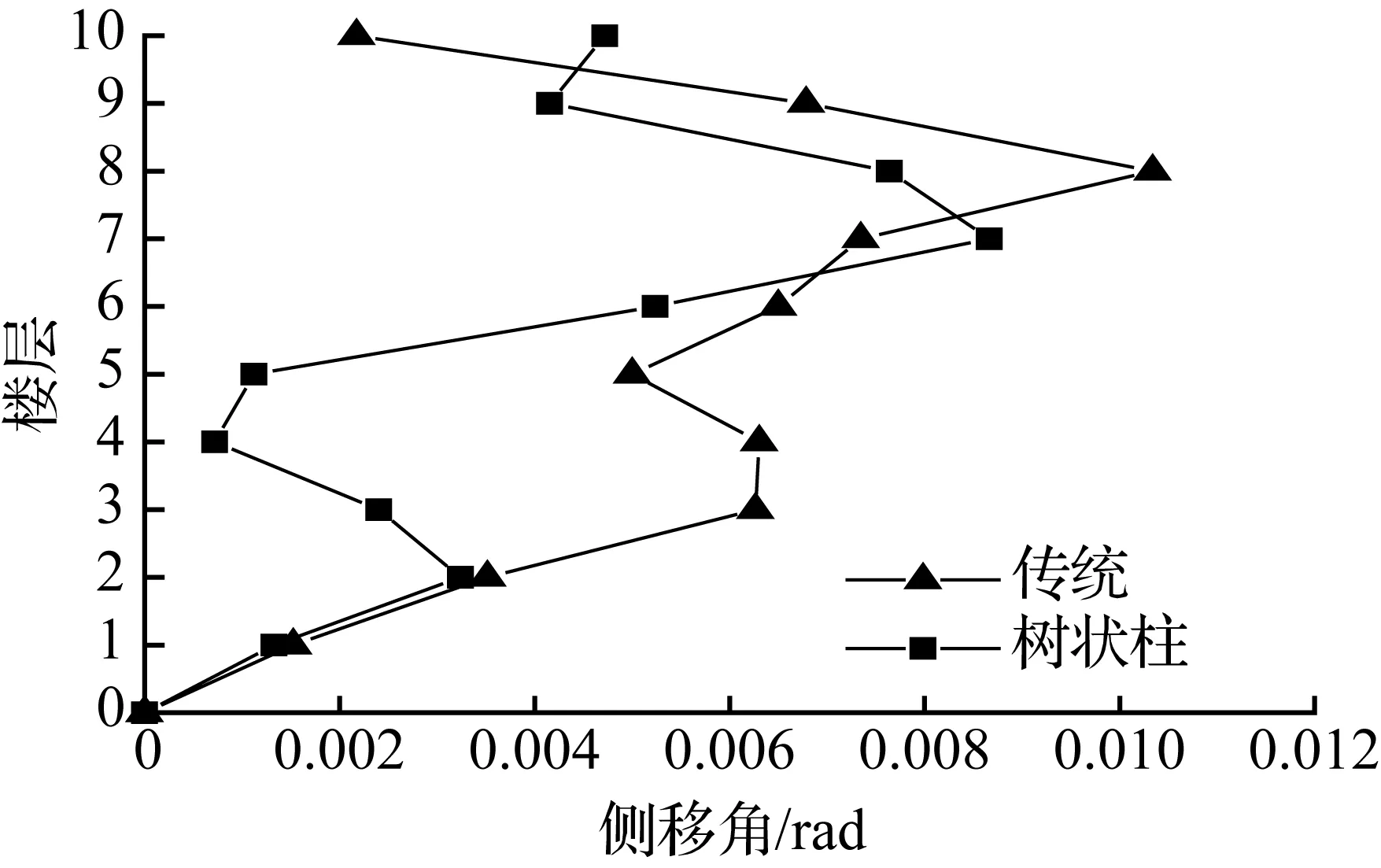
(d) 10层模型

图10迁安各模型顶层侧移最大时刻各层侧移角

Fig.10Story drift ratio of each story at the max drift of the top story for models in qianan earthquake

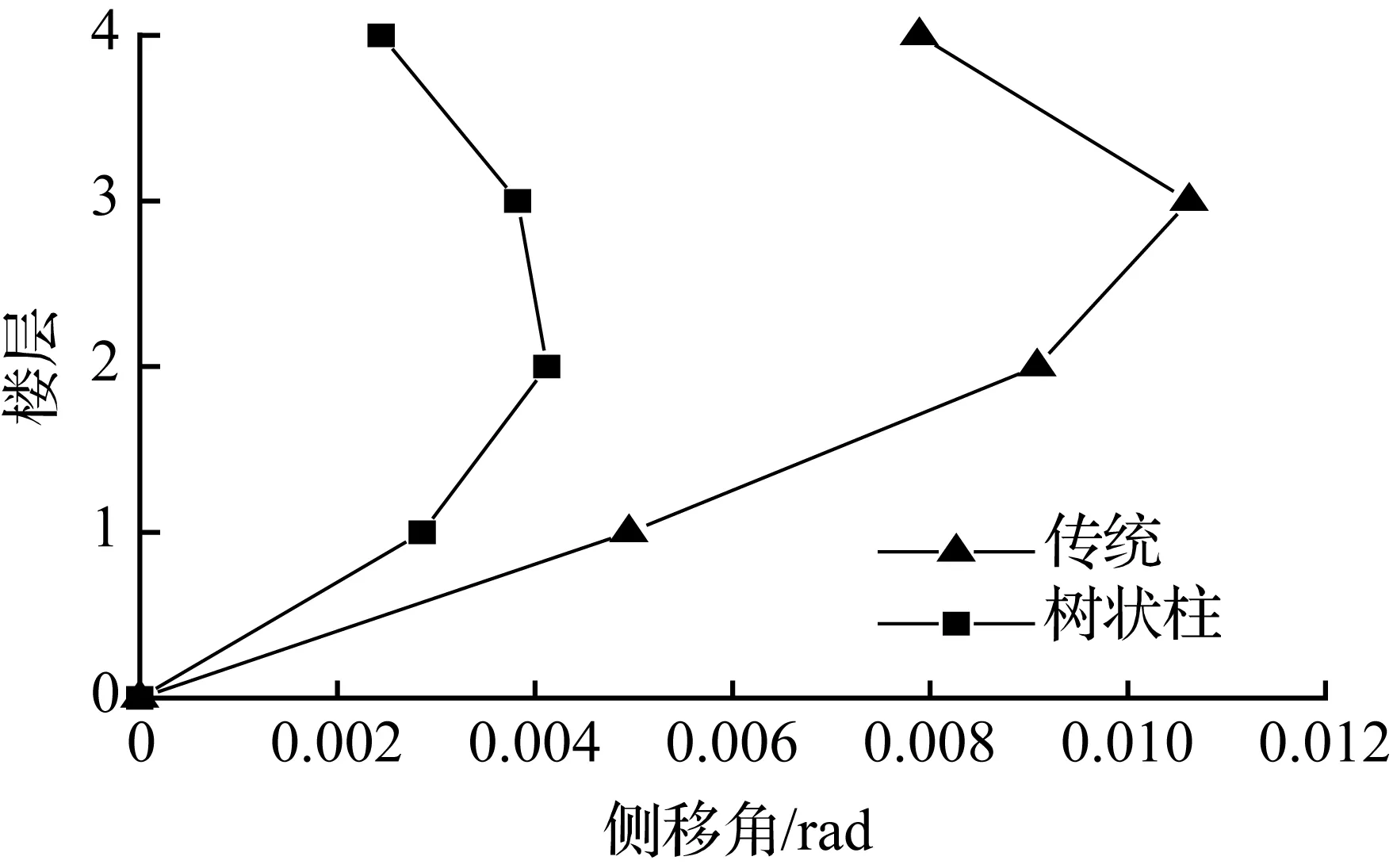
(a) 4层模型

(b) 6层模型

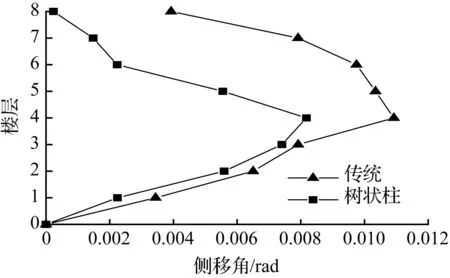
(c) 8层模型

(d) 10层模型

图11兰州波各模型顶层侧移最大时刻各层侧移角

Fig.11Story drift ratio of each story at the max drift of the top story for models in lanzhou earthquake

3.3剪力分析

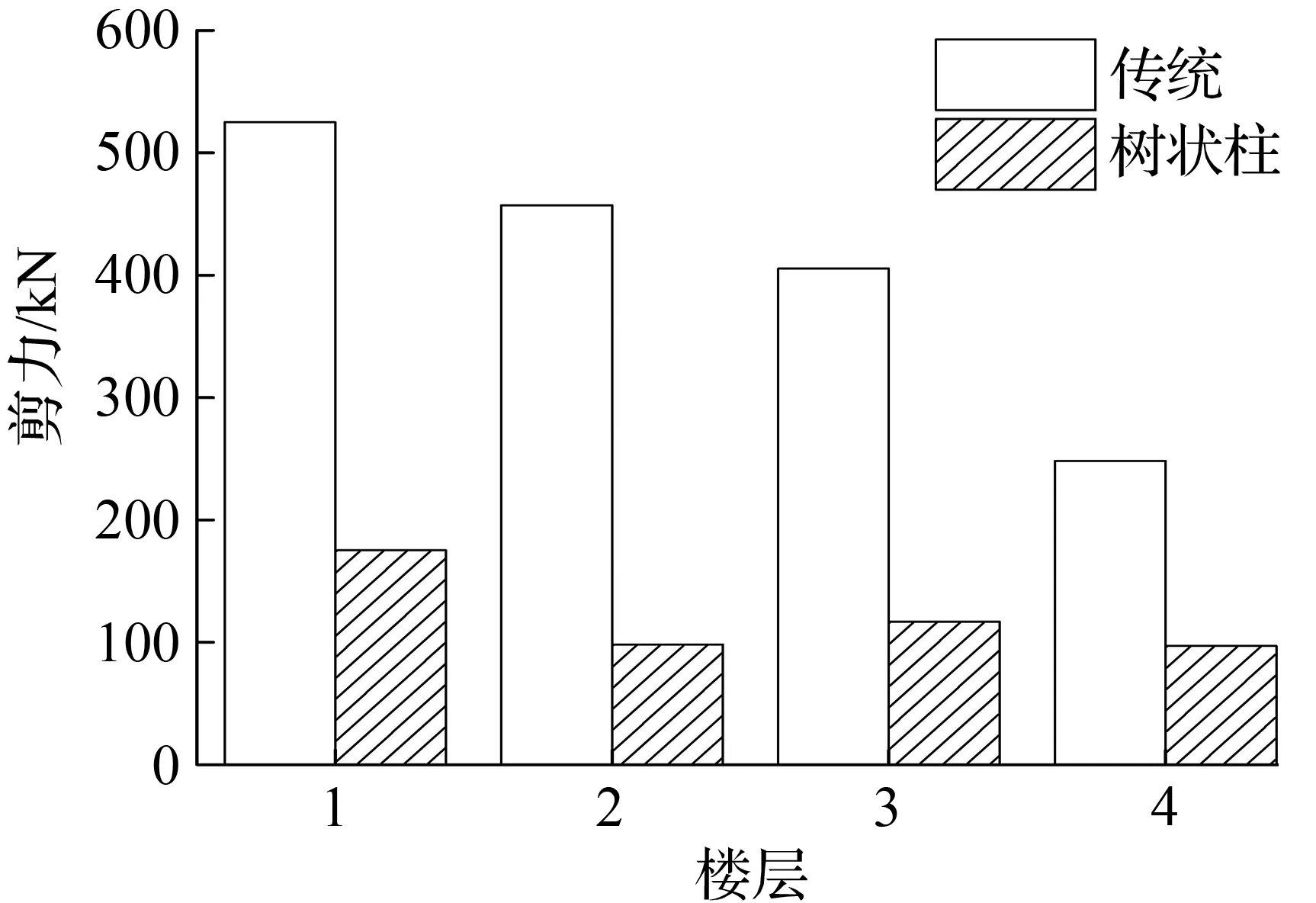
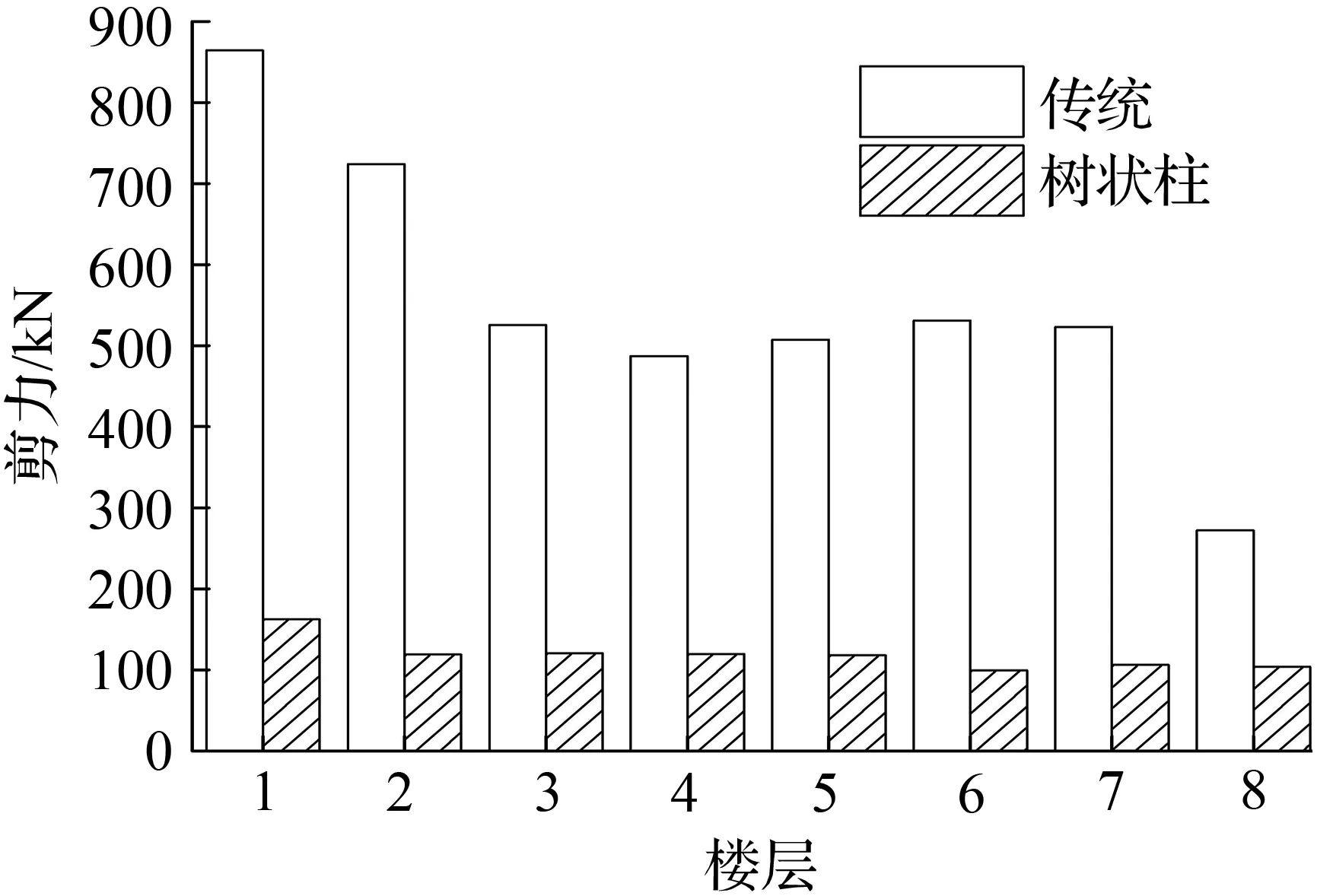
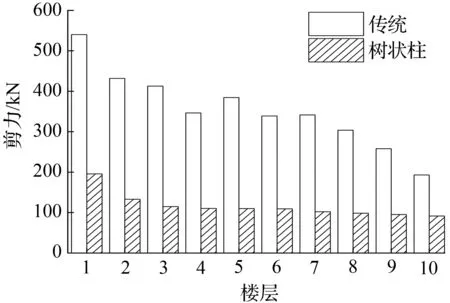
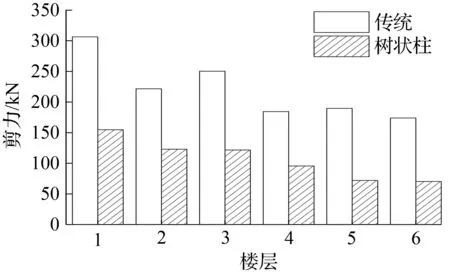
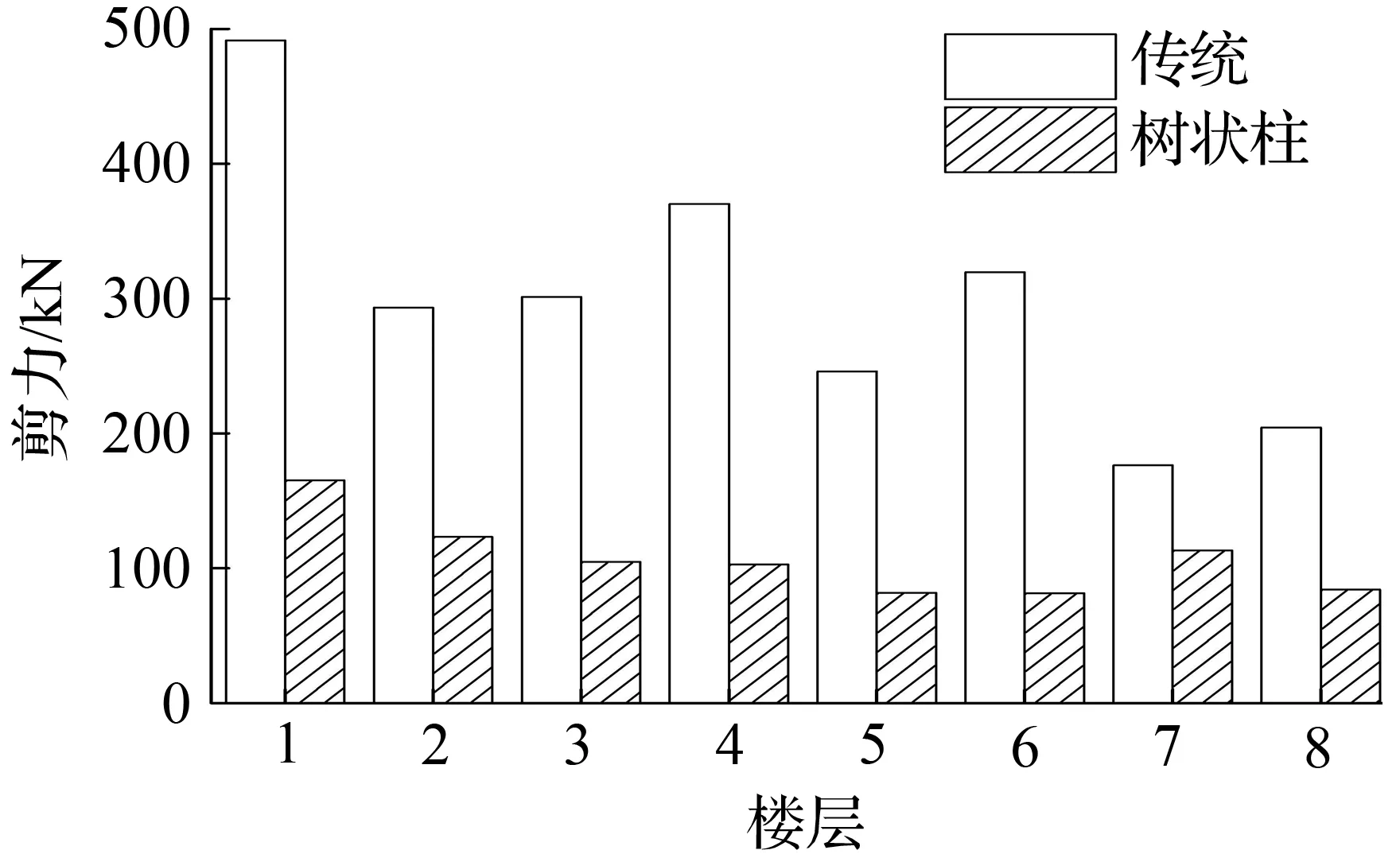
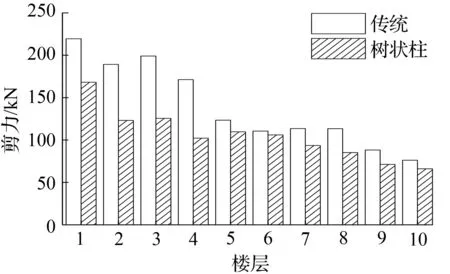
在地震波作用下，4种模型各层最大层间剪力曲线见图12～图14，各模型基底剪力最大值都没有超过钢柱的承载能力极限值。

①层数对树状柱钢框架基底剪力的影响

在地震作用下树状柱钢框架各模型基底剪力最大值见表5。从表5中可看出，总趋势是随着层数的增大，树状柱钢框架基底剪力最大值也增大。虽然El Centro波中8层模型和迁安波中10层模型的基底剪力最大值较小，但不影响整个变化规律。

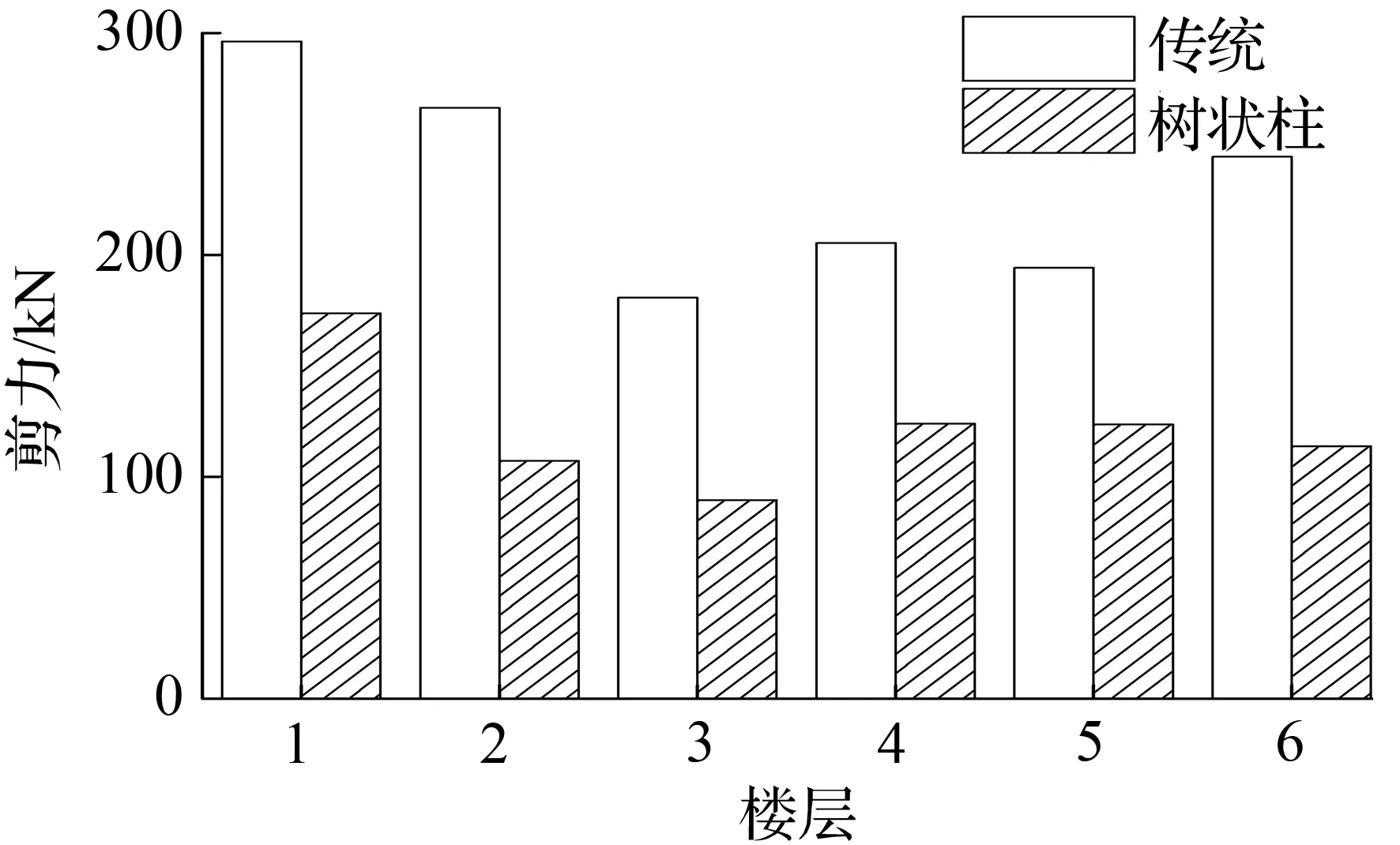
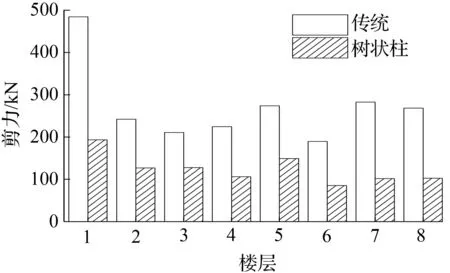
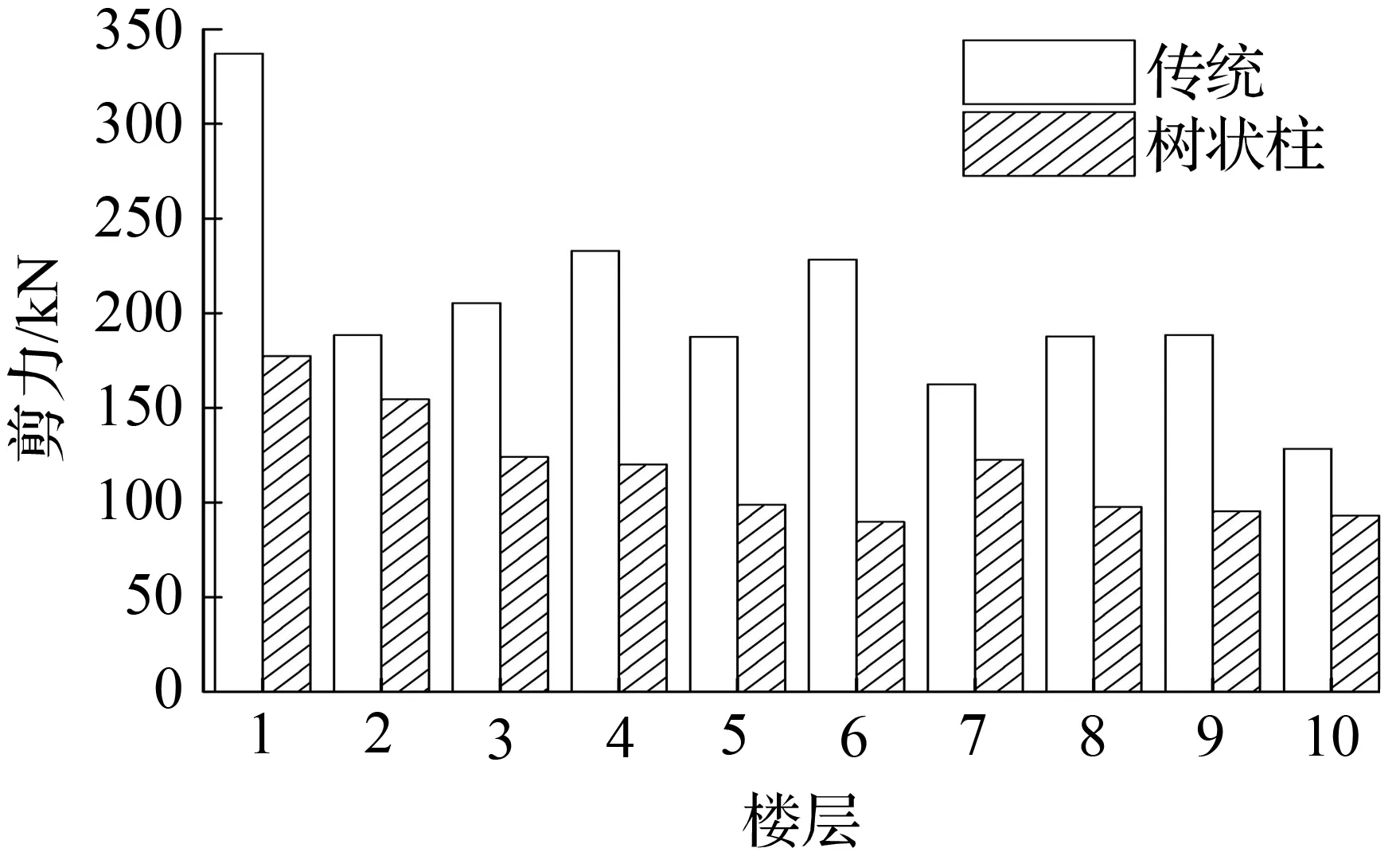
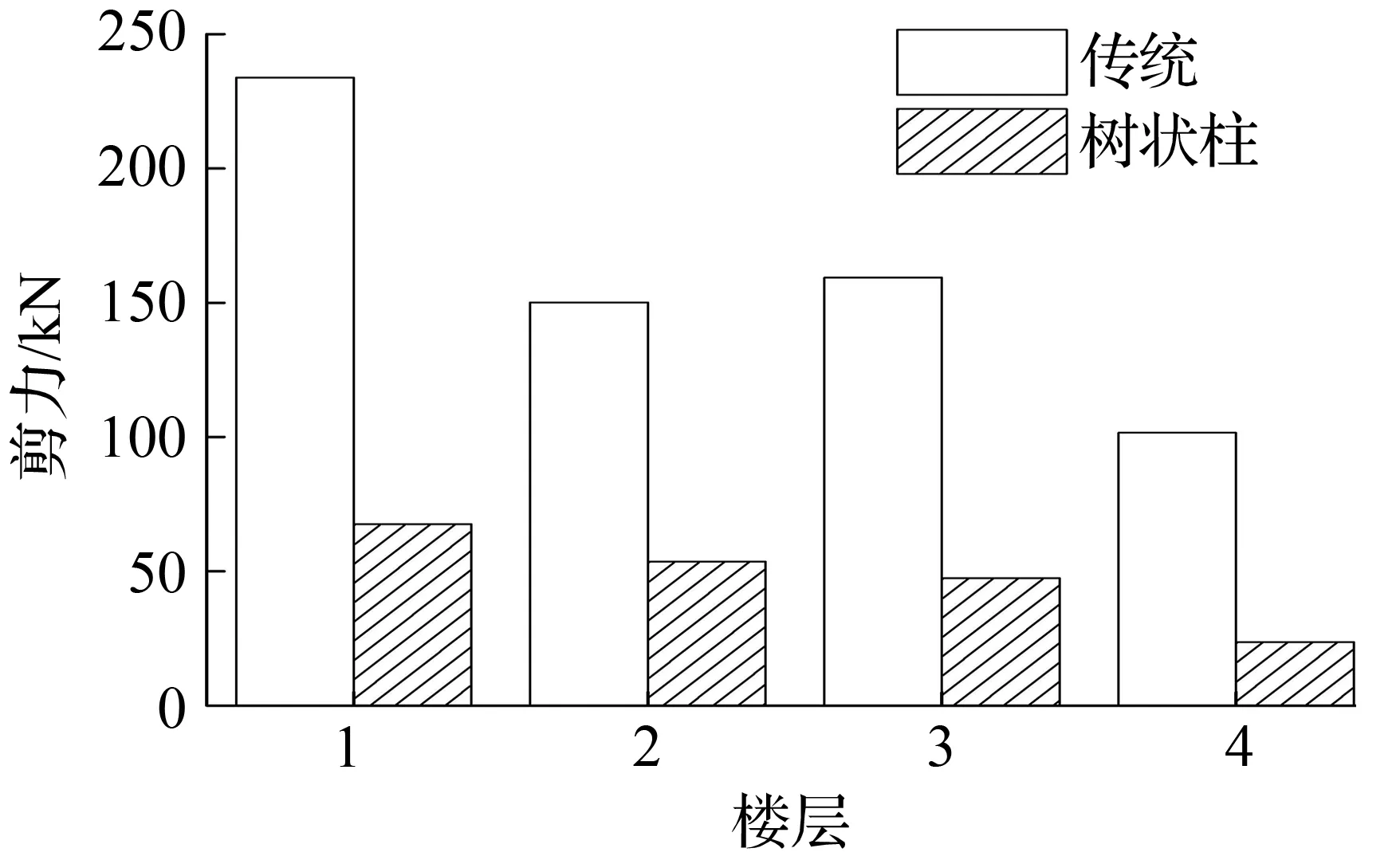
②树状柱钢框架和传统钢框架剪力的比较

从图12～图14中看出，树状柱钢框架各层剪力最大值小于传统钢框架各层最大剪力。树状柱钢框架基底剪力值减小比例见表5。由表5可看出，减小的幅度基本都在50%左右，最大幅度达到81.2%。基底剪力值的减小，可以减小底层柱截面尺寸，使得结构更加经济。

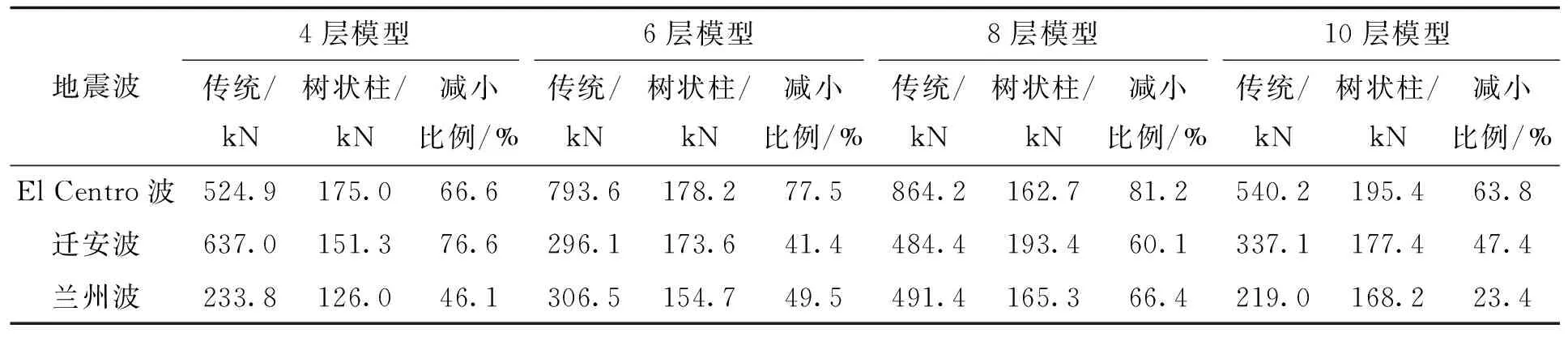
表5　树状柱钢框架和传统钢框架基底剪力及减小比例Tab.5　The reducing ratio and base shear force between column-tree moment-resisting frames and the traditional steel frame

(a) 4层模型

(b) 6层模型

(c) 8层模型

(d) 10层模型

图12El Centro波模型各层最大剪力

Fig.12The max story shear force of each story for models in El Centro earthquake

(a) 4层模型

(b) 6层模型

(c) 8层模型

(d) 10层模型

图13迁安波模型各层最大剪力

Fig.13The max story shear force of each story for models in qianan earthquake

(a) 4层模型

(b) 6层模型

(c) 8层模型

(d) 10层模型

图14兰州波模型各层最大剪力

Fig.14The max story shear force of each story for models in lanzhou earthquake

3.4模态与地震剪力系数分析

在有限元软件中对4种模型进行模态分析，得到传统钢框架和树状柱钢框架的自振周期。根据我国现行《抗震设计规范》5.2.5的要求，计算规范规定的楼层最小地震剪力系数值λ，具体数值见表6。从表6中看出，第一阶和第二阶振型分别都是沿x和y两个水平方向振动，第三阶振型都是绕z轴扭动。本研究设计的树状柱钢框架有限元模型楼层最小地震剪力系数值见表7。从表7中看出，树状柱钢框架有限元模型的地震剪力系数都满足建筑抗震规范要求。

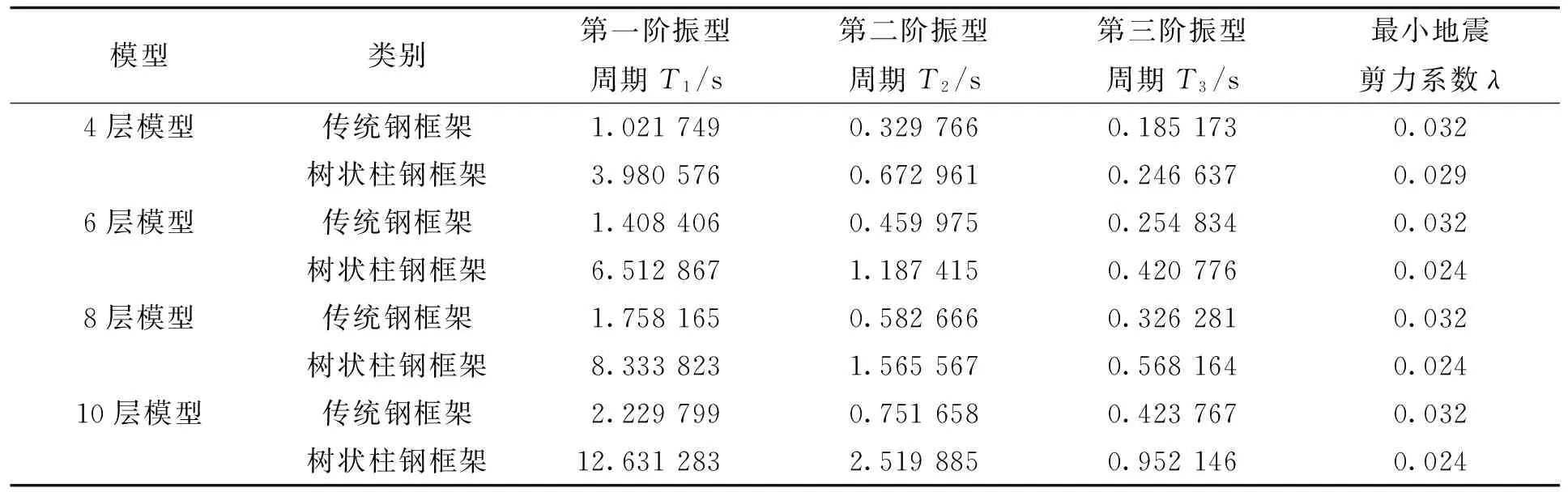
表6　模型前三阶周期和楼层最小地震剪力系数Tab.6　The first three periods of models and seismic shear coefficient

表7　树状柱钢框架有限元模型最小地震剪力系数Tab.7　Seismic shear coefficient of column-tree moment-resisting frame models

4　结　论

本文通过有限元分析，并与传统钢框架比较，研究按照实际内力设计钢梁拼接节点的不同层数的树状柱钢框架在地震作用下侧移、侧移角和基底剪力，得到以下结论：

①与传统钢框架相比，树状柱钢框架在低层和多层结构中，可以减小结构顶点最大侧移，由于高阶振型和共振的影响，兰州波作用下10层结构中，树状柱钢框架的顶点侧移大于传统钢框架顶层侧移。

②与传统钢框架相比，树状柱钢框架可以减小结构的层间侧移角。树状柱钢框架侧移角的变化比传统钢框架更加缓和，性能更好。

③与传统钢框架相比，树状柱钢框架能够显著地减小结构中基底最大剪力值，减小的幅度基本都在50%左右。

④加速度峰值相同的不同地震波由于频谱特性不同，对树状柱钢框架的侧移影响也不同。

[1]NAEIM F, JR R M D, BENUSKA K V, et al.Seismic performance analysis of a multistory steel moment frame building damaged during the 1994 Northridge earthquake[J]. Structural Design of Tall Buildings, 2006, 4(4):263-312.

[2]RAMIREZ C M, LIGNOS D G, Miranda E, et al.Fragility functions for pre-Northridge welded steel moment-resisting beam-to-column connections[J]. Engineering Structures, 2012, 45(2284):574-584.

[3]ASTANEH-ASL A, MCMULLIN K M.Steel semirigid column-tree moment resisting frame seismic behavior[J]. Journal of Structural Engineering, 2003, 129(9):1243-1249.

[4]李启才,苏明周,顾强,等.带悬臂梁段拼接的梁柱连接循环荷载试验研究[J]. 建筑结构学报, 2003,24(4):54-59.

[5]OH K, LI R, CHEN L, et al.Cyclic testing of steel column-tree moment connections with weakened beam splices[J]. International Journal of Steel Structures, 2014, 14(3):471-478.

[6]常鸿飞,夏军武,靳大勇.钢框架带悬臂梁段拼接节点的承载特性分析[J]. 建筑钢结构进展, 2008, 10(6):47-53.

[7]陈自全,彭修宁,林海.钢结构节点抗震措施研究[J]. 广西大学学报(自然科学版), 2008, 33(z1):11-14.

[8]GHOLAMI M, DEVLAMI A, TEHRANIZADEH M.Seismic performance of flange plate connections between steel beams and box columns[J]. Journal of Constructional Steel Research, 2013, 84(3):36-48.

[9]杨雪,曲激婷.考虑塑性铰外移的消能减震结构动力时程分析[J]. 沈阳大学学报(自然科学版), 2013, 25(5):398-402.

[10]张凤梅,王燕,刘芸.不同构造形式加强型节点断裂特性分析[J]. 青岛理工大学学报, 2013, 34(2):5-13.

[11]陈廷国,赵广军.钢框架延性节点塑性铰外移的机理研究[J]. 钢结构, 2014, 29(12):25-31.

[12]王斌,李启才.悬臂梁段拼接节点耗能的刚性钢框架时程分析[J]. 西安科技大学学报, 2011, 31(4):433-437.

[13]金龙.利用悬臂梁段拼接耗能的钢框架试验研究[D]. 苏州;苏州科技学院, 2014.

(责任编辑唐汉民裴润梅)

Seismic behavior of multi-story and high-rise steel column-tree moment-resisting frame

ZHANG Yong-xian, LI Qi-cai, HE Ruo-quan

(Structure Engineering Key Laboratory of Jiangsu Province, Suzhou University of Science and Technology, Suzhou 215011, China)

For further study on the seismic performance of steel column-tree moment-resisting frame with weakened splice joints, the trilinear model to simulate the splice joints was modified. 4-, 6-, 8- and 10-story steel column-tree moment-resisting frames with the actual forces on the splice joints were designed with the improved trilinear model. Elastoplastic time-history analysis on the aforementioned 4 frames under earthquake waves was carried out and compared with that on traditional steel frames without splice joints. The theoretical analyses demonstrate that the improved trilinear model is closer to the actual situation; that the steel column-tree moment-resisting frame with splice joints designed according to actual forces reduces base shear force and increases the period of the structure, and top story drift and inter-story drift ratio commonly reduce except for the 10-story frame under Lanzhou waves, whose story drift and inter-story drift ratio increase because of higher mode and resonance.

steel column-tree moment-resisting frame; time-history analysis; story drift; inter-story drift ratio; base shear force

2016-05-02；

2016-05-30

国家自然科学基金资助项目(51178285)；苏州科技大学科研基金项目(XKZ201204)

李启才(1969—)，男，河南灵宝人，苏州科技大学副教授，工学博士；E-mail：ustsgig@163.com。

10.13624/j.cnki.issn.1001-7445.2016.1024

TU391

A

1001-7445(2016)04-1024-13

引文格式：张永咸，李启才，何若全.多高层树状柱钢框架结构体系的抗震性能分析[J].广西大学学报(自然科学版)，2016，41(4)：1024-1036.