Mode5中调制解调的实现方法
2016-08-29四川九洲电器集团有限责任公司
四川九洲电器集团有限责任公司 葛 露
Mode5中调制解调的实现方法
四川九洲电器集团有限责任公司葛露
Mode5是北约现役识别系统全新设计模式,采用了高数据率的MSK调制方式。本文从理论出发,结合工程实践,针对Mode5调制解调提出简化的实现方式,可简化实现复杂度并节约硬件资源。
Mode5;MSK;正交调制;差分解调
1 引言
Mode5是北约现役MarkⅫA雷达敌我识别系统中全新设计的模式,是对原MarkⅫ敌我识别系统的改进。Mode5使用了现代的调制、编码和加密技术,克服了MarkⅫ波形的性能和安全问题,可提供高可信度、精确、连续的友军信息来防止误伤。
与原MarkⅫ相比,Mode5改进如下:采用MSK调制方式;询问信道和应答信道传输的询问和应答数据采用了高数据率最小相移键控(MSK)调制方式,由于MSK调制频谱占据带宽更窄,减少了对L频段其他系统的干扰,同时扩频技术的采用,可进一步提高系统的抗干扰能力。
下面对Mode5中MSK调制解调实现方法进行讨论。
2 调制
Mode5中采用了16MHz码速率的MSK调制方式。MSK调制方式的数学表达式为:

其中T为码元周期,dk为输入码元序列。MSK调制常见的实现方法为基带正交调制方式,基带调制分为频率和相位两部分,其中基带的余弦加权脉冲频率为固定值,由码片周期决定,对Mode5而言,加权频率f=4MHz;而相位部分则由初始相位和输入码元序列决定。MSK基带调制的相位完全由输入码元序列决定。当输入码元为1时相位在当前相位上增加90°,而输入码元为0时则相位在当前相位基础上减小90°,相邻码片实现正交。
工程上为实现调制方式,可考虑仅根据码片周期生成相应的载波,可采用ROM查找的方式代替原NCO,然后根据输入码元控制ROM地址实现MSK基带调制。考虑16位80MHz的时钟速率对码元进行调制,首先计算得到所需的基带载波信号,载波频率为f=4MHz,并用16比特二进制补码对数据进行量化,将所得到量化数据的生成ROM查找表,这里我们记录一个整周期的cos(2πft)余弦信号(20×16bit),如表1所示。

表1 整周期余弦表

图1 MSK调制路径示意图
对应的sin(2πft)函数与cos(2πft)相差为90°,对应的基地址在表1中为15,则无需单独进行记录。
当输入码元为1时,相位增大90°,输出对应地址空间增大5个单位,即从addri到addri+4;当输入码元为0时,相位减小90°,输出对应地址空间减少5个单位,从addri到addri-4。如调制码元dk=[1, 1,1, 0]时,基带输出地址空间变化如图1所示。
将I、Q数据序列按照时钟节拍送D/A完成数模转换,通过上变频到规定的频率实现MSK射频调制。
3 解调
MSK的解调有多种实现方式,工程上较为易于实现的为非相干差分解调的方式,实现原理如下:将射频信号进行抽取滤波后下变频至基带,I、Q两路信号可分别用表达式cos(θt)和sin(θt)表示,其中θt为t时刻码片的相位。将两路信号分别延时一个码片时间可得到上个码片的表达式cos(θt-1)和sin(θt-1),用I路的延时乘以Q路的当前值减去Q路的延时乘以I路的当前值满足
sin(θt)cos(θt-1)-cos(θt)sin(θt-1)=sin(θt-θt-1)=sin(Δθ)
当调制bit为1时,当前码片相对前一码片的相位增大90°,而调制bit为0时,当前码片相对前一码片的相位减小90°,即可通过上式sin(Δθ)的符号判断相邻码片相位的变化关系实现解调,即下式成立,流程如图2所示。从图2可以看出这里仅需要两个乘法器和少量逻辑资源实现MSK的解调。

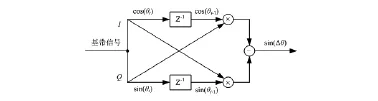
图2 MSK非相干差分解调流程图
通过HDL实现并在Modelsim中进行仿真验证,得到的时序波形如图3所示,其中data_org为编码数据,data_dec为译码数据。

图3 差分解调仿真时序图
4 结论
本文从工程角度提出了一种Mode5调制解调的实现方式,经过实际验证是一种可行的方式,可以简化实现的复杂度、节约硬件资源,且满足系统指标的要求。
[1]DoD AIMS 03-1000A.
[2]仇佩亮,陈惠芳,谢磊.数字通信基础[M].电子工业出版社.
