揭开哲学现代科学形态的神秘面纱——读《广谱哲学浅说》的两个启示

杨国斌

(华北水利水电大学 马克思主义学院，河南 郑州 450046)



揭开哲学现代科学形态的神秘面纱

——读《广谱哲学浅说》的两个启示

杨国斌

(华北水利水电大学 马克思主义学院，河南 郑州 450046)

广谱哲学提出，哲学应该具有现代科学形态，即应该走“广义四化”(广义的公理化、模型化、数学化、程序化)的道路。这种一反思辨之说、反思之说的论断，使哲学界许多学者感到惊讶和不解。《广谱哲学浅说》一书，以通俗易懂的方式，系统地回答了两大问题：一是哲学为什么要走“广义四化”的道路，二是“广义四化”是否使哲学变成了具体科学，即是否使哲学丧失了之所以为哲学的资格。

广谱哲学;现代科学形态;“广义四化”道路

作为广谱哲学创始人，张玉祥教授很早就为广谱哲学设计了“广义四化”的目标，即广义的公理化、模型化、数学化和程序化的目标，并把这“四化”看成是哲学具备现代科学形态的基本标志。如果从1989年《关于哲学的规范化道路》一文算起[1]，张教授已为实现这一目标奋斗了25年，并取得了丰硕的成果。毋庸置疑，“广义四化”的道路在哲学界不仅是没人走过的路，而且用“四化”的形式表达出来的种种成果(主要是论文和专著)，很多人或者不感兴趣，或者难以看懂。这里有两个绕不过去的问题，一是哲学为什么要走“广义四化”的道路？几千年的哲学由于没走“广义四化”的道路停止前进了吗？二是经过“广义四化”的改造(假定这种改造是正确的)，解决了哲学上的什么问题？人们特别关心的是，经过这种改造，哲学还是哲学吗？它是否退化成了具体科学？

可以认为，张玉祥教授的新著《广谱哲学浅说》(以下简称《浅说》)以生动形象的语言，深入浅出的阐述，系统且彻底地回答了这两个问题。

一、哲学为什么要走“广义四化”的道路

先说“广义四化”的公理化。直白地说，公理就是给定一组含义明确的前提，由这组前提可以推理出若干明确的结论(在数学上就是定理)。例如，由“过已知直线外的一点能够作且只能作一条直线与已知直线平行”这一公理，可以推出“三角形内角之和等于180°”这一定理。所谓公理化，是指对一个理论体系，要找到或选择一组这样的公理(前提)。当然，这组公理或前提之间不能互相矛盾(称为相容性)、不能互相导出(称为独立性)、不能在后面的推导中不够用(称为完备性)。然后，利用逻辑推理规则，从这组公理推出该理论体系中的所有结论(定理)。

由于哲学概念、命题的惊人庞杂性(理论流派之多、矛盾对立之多)，不用说要抽出一组“公认”的公理(前提)有多难，既使要满足上述的相容性、独立性、完备性也并不简单。例如辩证法的许多辩证范畴之间就具有内在一致性、相通性。例如个别和一般、差异和同一、现象和本质在集合论的等价关系的意义上没有实质的区别(见《浅说》第26章)。因此纯粹的独立性是不可能的。至于完备性只能是一种探索过程。因此，广谱哲学提出了广义公理化的要求，包括分块公理化、分块完备化和逐渐逼近化等内容。

最为根本的问题是，哲学何以必须走(广义)公理化的道路？《浅说》以列宁对普列汉诺夫的一段批评为例，揭示了这一问题的实质。列宁对普列汉诺夫把对立统一规律这样一个普遍的规律当作“实例的总和”加以解释不满意。所谓“实例的总和”就是某一哲学原理具有最高普遍性，但它是预先给定的，要证明它的普遍性要靠举大量的实例。但“实例的总和”总是有限的，它不能证明该原理的普遍性(无限性)。应该说，列宁的这个批评直到今天仍有现实意义，因为我们沿用到今天的哲学教科书仍是“普列汉诺夫式”，即到处充斥的仍是“哲学原理+实例”。广谱哲学认为，要跳出这一窠臼，只能走(广义)公理化的路子，即普遍性的哲学命题、规律只能由选定的公理导出，而不是靠举实例。

再说“广义的模型化”。一般地说，给定一个客观事物系统(它往往是相对复杂的)，通过简化，抓住其主要的关系、结构，并将其制造或描述出来，则原初的客观事物系统称为原型，而制造物或描述的结果称为该原型的模型。例如太阳系是一个客观事物系统(原型系统)，哥白尼通过多年的天文观测和理论分析，确定了以太阳为中心、行星绕日运动(关系结构)的事实，提出了著名的哥白尼学说。哥白尼学说就是太阳系的一个模型(称为物理模型)。

广义的模型不限于物理模型、生物模型(如用小白鼠、猴子等做病理实验等)，还可以有概念模型(如当物体的大小和形状可以忽略不计时，用质点代替物体)、理想实验模型(如忽略了摩擦的斜面实验)、结构模型(如用关系图模拟客观事物的关系)、逻辑模型(用逻辑关系模拟客观事物或案件的因果关系)、数学模型(如用方程模拟客观事物之间的数量关系)等等。

广谱哲学认为，任何模型(狭义的和广义的)都是原型系统的抽象结构表达。这里“抽象结构”有两层含义。其一是指模型是对原型系统“抽取出来的影像”(简称“抽象”)。这时模型是对原型的简化，它以舍弃了原型事物若干特质为代价。正如摄影把一个三维(立体)的物体变成了一个二维的影像(平面图形)一样。牛顿的天体力学则是把行星、太阳看成是质点(只考虑质量、不考虑大小和形状)的绕圆(或椭圆)的周期运动。其二是指这种模型化以保留原型系统的稳定结构为前提。这里的“结构”即事物之间的基本关系。例如哥白尼的太阳系模型、牛顿的月地模型，虽然把行星(如地球)、卫星(如月亮)看成质点，但都保留了行星绕日运动，月亮绕地球运动的基本结构关系。

广谱哲学说的“广义模型化”是指哲理(哲学的基本概念、命题、原理等)的抽象结构表达。这时哲理是广义的原型，而对它们的抽象概括、结构表达是广义的模型。例如，《浅说》中一个典型的例子是：什么是“客观存在”?广谱哲学根据列宁的物质定义(可概括为“不依赖于人的意识而又能为人的意识所反映”的一切客观实在)，把“能够为人的意识所反映”抽象为“任意对象物，通过一定的观控方式(广义的反映方式)，变成人能够把握的一定影像”，而把“不依赖人的意识”抽象为“在一定的观控方式下，对同一对象物，n个人或n次的观控结果”一致，这就把客观存在变成了满足两种特定关系(结构)的对象物，前一个条件是一种特殊的映射(即满射)，后一个条件是等价关系，于是，列宁的物质定义(原型)就转化成了一种稳定的结构——n重观控下的不变性(不变的性质、不变的关系或不变的结构等)。

在广谱哲学看来，广义模型化的实质是寻求某个哲理(哲学的基本概念、命题、原理等)的稳定的结构内核，它不随语境的变换而变(这是“稳定”的含义)，如果抓不到这个稳定的结构内核，就会产生歧义，导致混乱，这是哲学问题(哲学的概念、命题、原理等)长期争论不休的根本原因之一。

再说“广义的数学化”。通常说的数学化(广谱哲学称为“狭义数学化”)是指对一个客观事物系统或该系统的运动变化，用某个数量关系结构表示。例如通常的代数方程、微分方程、差分方程等。这种数学化的好处，一是把研究对象精确化(即数量化)了，从而可用来比较排序。二是可以在此基础上进行运算推演(如对方程进行运算推演)。三是可以依据这种推演进行预测。

《浅说》一书多次指出，哲学问题不同于客观事物系统，它是“概念之上的概念”“命题之上的命题”“原理之上的原理”，不可能有明确具体的数量关系、函数关系、可微可导的关系等。例如存在和意识的关系(“存在决定意识、意识反作用于存在”)、现象和本质的关系(“本质决定现象，现象反映本质”)等等。这里，在哲学的层面上，狭义的数学化就失去了意义。

广谱哲学认为，我们虽然不能对哲学问题进行狭义数学化处理(用数量关系、变量关系等进行表示)，但却可以进行广义数学化处理。当我们把集合看成是任意事物的集合(不限于数量或变量的集合)，把关系看成是任意事物之间的关系，而不限于是数量或变量关系，把结构看成是任意事物之间满足一定公理的关系，而不是数量或变量之间满足一定(数量或变量之间的)公理的关系，等等，那么，我们便可以在抽象集合论、抽象代数论、抽象群论、抽象图论等基础上，对哲学问题进行广义量化(区别于数量化)的处理。

例如，《浅说》中给出的客观存在的等价关系(或抽象变换群)模型、量变与质变关系的等价类变换模型、能动反映论的多种映像模型、现象本质关系的同态模型、价值观中的广义供求条件模型、价值场网及其调控模型等都是广义数学化的典型例证。

类比于狭义数学化，广义数学化的好处，一是把哲学问题(概念、命题、原理等)的稳定的结构内核和一定的抽象数学结构联系起来，从而在广义上实现了哲学精确化。这时我们虽然不能处处比较数量的大小，但却可以比较集合的大小，关系的优劣，或者结构的异同(如同态与同构)等。二是可以在抽象集合论、抽象代数论、抽象图论等基础上进行运算和推演。三是通过这种运算和推演，可以模拟、检验传统哲学理论的严密性，便于发现问题，获得新结论。

例如，广谱哲学通过人的认识方式(广谱哲学称为观控方式)转化为一种特殊的映射——满射，不仅清晰地解释了马克思主义认识论中的一些基本观点*：例如无论是男女关系、夫妻关系、朋友关系、上下级关系等等，在集合论的意义上，都是直积的子集合。，而通过这种映射的组合、复合和变换模拟了能动反映论的多种典型情况。特别是，广谱哲学揭示：在指定的观控方式下，n个人或n次(n在理论上是无穷大)的观控结果不变(在数学上叫做落入同一个等价类内)，那么这种不变性(不变的性质、关系、结构、过程等)就是事物的客观性，称为单叶客观性，它是“真理只有一个”的客观依据。但当观控方式改变时，事物将由一种客观性转化成另一种客观性，这就是事物的多叶客观性。它是“真理可以有多个”的客观依据。

最后谈一下“广义的程序化”。简单地说，程序化就是干一件事，先干什么后干什么，要有个先后或优先次序。很多情况下，这个次序是不能颠倒的。如果颠倒，程序化就失去了意义。通常各个学科领域所说的程序化是比较严格的，例如计算机编程，要通过算法语言，每一步都必须“按步就班”，不允许中间跳过某一具体环节，否则计算机无法执行。医疗工作也是最讲程序的，否则会出医疗事故。其他如实验程序、施工程序、法律程序等有类似的问题。哲学是最不讲究程序的，因为它没有具体的目标，而是某个抽象的目标。例如由于本质决定现象，因此，它要求要透过现象看本质。这里本质就是一个抽象的目标。因为不仅不同的事物有不同的本质。而且同一个事物，由于人们探索的目的不同，要找的本质也不同。例如对同一个学生，辅导员要找的是该生心理障碍在哪儿，而校医要找的是该生的生理病灶是什么。在传统哲学看来，由于本质是个抽象的目标，因此，只能提要求(即要透过现象看本质)，至于如何找到这个抽象的目标，不可能规定程序。《浅说》先是剖析了现象和本质的结构特征(第26章)，揭示了“本质是同类现象的共同性质”的实质，而“同类”现象“无非是某种现象的一个等价类，这时该等价类的公共性质就是该种现象的本质。因此规定同态映射的程序就是透过现象看本质”的程序。这个(哲学)程序的特点是：它只抓住现象和本质(抽象目标)的内在的、根本的联系(特定的同态映射)，规定若干绕不过去的基本环节，及其优先次序，而基本环节的过渡(从甲环节到乙环节的实现)是不管的，那是具体科学的任务。这也为创造性思维提供了空间。这正是广义程序化的含义。

过去讲“世界观就是方法论”，其实只是视角的转换，即产生了某种哲学观点(世界观)，然后用这个观点去观察世界。而广谱哲学的“广义程序化”，把世界观真正转化成了方法论，使哲学方法论由不具有可操作性变成了有(广义的)可操作性，同时也在哲学与实际应用之间架起了一座桥梁。

二、“广义四化”是否使哲学变为具体科学

我们在上面不仅回答了哲学为什么要走“广义四化”的道路，也同时从四个方面回答了“广义四化”解决了什么问题。这就是“广义的公理化”使哲学跳出了“原理+实例”的怪圈；“广义的模型化”使每个哲学概念、命题或原理找到了稳定的结构内核，并用一定的模型使之固定下来；“广义的数学化”使哲学概念、命题或原理在广义量化(非数量化)的意义上实现了精确化；而“广义的程序化”使哲学方法论具有了可操作性，等等。那么，“广义四化”是否使哲学变成了具体科学。

答案是否定的。先说“广义的公理化”。它是指抽取一组最普遍的(这也是“广义的”含义之一)命题作为前提，由此作为推理的依据。例如广谱类变论中的两条公理(参见《浅说》第25章)：

公理1.任何客观事物都处在某个等价类中。

公理2.任何客观事物的性质都是它所处的等价类的共同性质。

在这两个公理中，指称对象是“任何客观事物”，因此可以广及自然、社会和思维领域(如概念是“精神事物”)，而“等价类”是“任何具有相同性质的事物类”，它一是没有限于任何特定的领域，二是没有限定哪一种特殊性质，因而不限于哪门具体科学。

作为对比，我们来看一下自然科学(理论力学)的一组公理：

公理1.力的平行四边形法则：作用在物体上同一点的力可以合成一个合力，合力的大小和方向，由这两个力构成的平行四边形的对角线确定。

公理2.二力平衡条件：作用在刚体上的两个力，使刚体保持平衡的充要条件是，它们大小相等，方向相反，作用在同一直线上。

在这两个公理中，指称的对象是“物体”或“刚体”，物体或刚体之间的关系是“力”(物体或刚体间的机械作用)。因此，这两个公理没有超出力学领域，甚至也没有超出刚体力学领域(例如理论力学只研究运动效应，即物体运动状态的改变，而不研究变形效应)，当然更没有超出自然界的范围(例如这两个公理不适用于生物界)，至于人类社会就更不用说了。

“广义的模型化”是指对哲学问题(哲学的概念、命题或原理)抽象结构的表达。这里表达的对象是“哲学问题”，按《浅说》第一章的解释，哲学问题是具有最高普遍性的问题。而这里的“抽象结构”是哲学问题的“稳定的结构内核”，因此，广义的模型化实质上是对最普遍的哲理的结构内核的形式表示。这与具体科学的模型化有着质的区别。

例如在牛顿力学中，要研究地球绕太阳旋转的运动，由于地球与太阳的平均距离比地球的半径大得多，地球上各点相对太阳的运动可以看作相同，因此可以忽略地球的形状和大小，而把地球简化为一个质点(只考虑质量)来处理，这就是一个理想化的物理模型。其他行星绕日运动的模型也一样。这些行星绕日的模型，尽管将行星的大小和形状抽象，只保留了行星绕日运动的椭圆形轨道，因而适于一切行星绕日运动的情况。但它仅限于绕定点的旋转这种特殊机械运动情况，而对于其他的运动(如弹簧振动)则不再适用。甚至电子绕原子核的运动也不再有圆形、椭圆形的清晰轨道，更不用说人才的成才道路，人们分析问题、解决问题的思路等，根本没有什么几何形状的轨迹可寻。与此形成鲜明对照的是，广谱哲学讲的“轨道”是任意事物组成的等价类，当一个事物的运动变化在该等价类内部变化时，就是广义的量变(称为同类变)，而当事物从一个等价类(一条轨道)跃迁到另一个等价类(另一条轨道)时，就是广义的质变(称为异类变)。这个(广义的)量变质变模型不仅适合于力学、物理学、化学、生物学等自然科学，也适合社会事物乃至于人的思维的量变质变现象。因此，它绝没有因模型化而退化为具体科学。

“广义的数学化”是指为哲学问题(哲学的概念、命题或原理)建立广义量化的数学模型。上面已说到“哲学问题”的最高普遍性，而“广义量化的数学模型”是“不依赖于数的数学”模型(参见《浅说》第二编)，其中“广义量”是指任意事物的集合、任意事物之间的关系、任意事物集合之间的映射、任意事物集合上的变换等等，“广义量”的运算也不再是数量的“加减乘除”等运算，而是任意事物集合的组合(并、交、差、补等)、任意事物之间关系的复合等“广义运算”。因此，“广义的数学化”是为哲学问题建立相应的数学模型，即哲学问题的普适面有多宽，数学模型的普适面就有多宽。人们之所以担心哲学问题的数学化会使哲学退化为具体科学，原因在于对“数学化”的狭义理解，以为数学就是关于数量关系的科学，他们走不出来的一个“陷阱”是“没有数量关系，哪儿来的数学？”无论如何也不相信还有一种“不依赖于数的数学”(《浅说》第二篇标题)。这是一个很大的台阶，甚至是很多人终身难以逾越的台阶。例如从具体的函数形式(如，y=kx+b,y=sinx等)到一般的函数概念(自变量与因变量的关系，如y=f(x))，人们是容易理解的，因为这里的x、y还限于数量或变量。当把函数的概念推广为映射f:A→B时，就开始上了一个台阶。因为A和B可以是任意事物的集合(不限于数量或变量)。例如A和B可以是任意事物关系的集合、结构的集合、事件的集合、过程或状态的集合等。特别地，当映射为满射f:A→f(A)时，f可看成人观察、控制研究对象的方式，即认识论讲的反映方式，这时f(A)是反映结果的集合，f(A)={f(x)|x∈A}，这里的仍代表任意事物、任意事物之间的关系、结构、事件等等。而是的广义影子，它可以是客观事物的非数量性状，对的某种评价(价值判断)等。显然，这一步对许多人来说，又是一个台阶。

进一步地，如果对于满射再进行组合(如取映射幂)、复合(运算)、变形等，则可以模拟各种能动反映形式，这是第三个大的台阶。经过这三大台阶的概括、抽象、扬弃，只剩下了哲学认识论层面的抽象关系结构，而与具体科学(如数学上的函数理论、应用函数理论的各门自然科学等)有了天壤之别。

狭义的程序化是针对特殊系统(如科学实验系统、医疗卫生系统、法律系统等)的特殊要求而规定的程序或优先次序。如前所述，广义的程序化是哲学方法论层面(即最一般的方法论层面)的程序，它不针对某个特殊系统，而是任意系统。例如根据辩证法普遍联系的观点，要求“全面地看问题”，要“统筹全局”，不能“以偏盖全”等。

这里的“以偏盖全”(例如“盲人摸象”)是先指定一个系统(如大象)，其次是限定在某个局部(如大象的腿)，然后用该局部的性状取代全局的性状(如说大象是柱子)。因此，“以偏盖全”的程序是[2]：

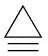
其中“扩展原系统”是为了把原系统放到更大的范围内去考察(全局的观点)，“正确分类”是指选好分类标准(数学上是一个等价关系)再分成若干子系统(数学上叫商化)，“协调优化”属于“运筹学”的范畴。这个程序也不是针对哪个特殊系统的，而是适合于任意系统的、属于哲学层面方法论的程序化，它不会使哲学方法论退化为具体科学的方法论。

三、结语

本文通过对《浅说》一书关于建立哲学现代科学

形态四个标准(广义的公理化、模型化、数学化、程序化)的解读，回答了两个方面的问题。第一个方面是哲学为什么要走“广义四化”的道路？理由有四：一是不走“广义公理化”的道路，哲学永远走不出“原理+实例”的怪圈，即哲学永远是“实例的堆砌”，不可能形成逻辑严密的体系。二是不走“广义模型化”的道路，哲学问题(概念、命题、原理等)就找不到稳定的结构内核，就会“公说公有理，婆说婆有理”，就会歧义百出，争论不休。三是不走“广义数学化”的道路，哲学问题就不能实现(广义的)精确化，就会在思辨的、反思的、观念的牧场中兜圈子(费尔巴哈语)，而不能一步一个脚印地使哲学有“看得见的进步”。四是不走“广义程序化”的道路，哲学方法论就会永远停留在世界观的层面(即所谓“世界观就是方法论”)，而不会有(广义的)可操作性，就截断了哲学和实际应用之间联结的桥梁和纽带。第二个方面是“广义四化”是否使哲学变成了具体科学？回答是否定的。正如《浅说》反复论证的：无论是“广义的公理化”“广义的模型化”，还是“广义的数学化”“广义的的程序化”，都需要满足哲学问题(哲学概念、命题、原理)的“最高普遍性”“最大跨域性”的条件，而这两个条件，是哲学之所以是哲学的根本标准，是区别于所有具体科学的最后界限。

[1] 张玉祥.关于哲学的规范化道路[J].华北水利水电学院学报(社科版),1989(1)：30-34.

[2] 张玉祥,常晓辉.浅谈广谱哲学的三个特点[J].自然辩证法研究,2014(7):120-124.

(责任编辑：张胜前)

Uncovering the Mysterious Veil of the Modern Scientific Form of Philosophy—Enlightenments fromAnElementaryIntroductiontoBroad-spectrumPhilosophy

YANG Guobin

(School of Maxism, North China University of Water Resources and Electric Power, Zhengzhou 450046, China)

What is philosophy? The philosophical field seldom raises such questions. Broadspectrum philoshophy points out that philosophy should possess the modern scientific forms, ie. it should follow the generalized four-standardization route (generalized axiomatization, modelization, mathematization and procedurization). These doctrines of speculation and reflection startled and puzzled many philosophical scholars. In a simple way,AnElementaryIntroductiontoBroadspectrumPhilosophyhas systematically answered two questions: 1) why philosophy should follow the generalized four-standardization route; 2) whether the “generalized four-standardization” has turned philosophy into a specific science, ie. whether it has deprived philosophy of its philosophical qualification.

broadspectrum philoshophy; modern scientific forms; generalized four-standardization route

2015-12-03

杨国斌(1971—)男，河南温县人，华北水利水电大学马克思主义学院教授，博士后，研究方向为马克思主义理论。

B089

A

1008—4444(2016)03—0005—05