例谈章节起始课情境设置的目标指向

江苏省木渎高级中学　(215101)　孙夏珍江苏省苏州实验中学　(215011)

丁益民



例谈章节起始课情境设置的目标指向

江苏省木渎高级中学(215101)孙夏珍江苏省苏州实验中学(215011)

丁益民

章节起始课作为一章之首，具有引领与统摄的地位，起着先行组织者的作用，在宏观上往往会呈现整章内容的知识脉络与发生过程．“好的开始是成功的一半”，作为起始课中的情境设置便显得尤为重要，笔者认为，起始课中情境设置的目标指向直接关系到学生的学习定位与目标达成.因此，章节起始课的情境设置应仅仅围绕教学的目标指向进行设置，本文借一些具体案例谈谈个人的一些思考，敬请指正.

1.情境设置应体现整章的核心思想方法

章节起始课的教学内容往往蕴涵着本章的核心思想方法，在章节学习的开始阶段就要让学生有所感知.信息加工理论告诉我们，学生最先获得的信息会在脑海中形成认知对象的“第一印象”，并使其思维形式固定下来.为了帮助学生获取正确而积极的“第一印象”，应创设出能体现整章核心思想方法的情境，让学生通过具体情境初步感受核心思想方法的存在与价值.

案例1苏教版必修2第2章“解析几何初步”的起始课“直线的斜率”(借班上课)

图1

问题：第一次和大家见面，可我却很用“心”，瞧！一颗红心代我心，(生笑)请问，用什么方法可以准确完美地画出这幅“心形图”呢?

引导启发：“心形图”是一条曲线围成的平面区域，我们可以先画出“心形”曲线，根据点动成线，只要画出“心形曲线”上每一个点即可，那么“点”是怎样准确画出来的？

生：在平面直角坐标系中可以用坐标画出.

师：要画出所有点的坐标是不可能的，是否可以找到“心形曲线”上所有点的横坐标与纵坐标的关系，根据“关系”作出图形呢？

生认可.

根据学生群体的年龄特点，改编了笛卡尔的“心形图”故事，不仅自然化解了师生初次见面时的陌生境况，还充分调动了学生的学习积极性.情境中的“作图”蕴含的思想方法将会引发学生认知观念上的冲击与思考，学生从中能初步感受到用代数方法研究几何问题的“奥秘”，而这一最初的认知观念在即将学习到的“直线的斜率”内容将会具体实践，并在以后的“直线的方程”、“圆的方程”、“圆锥曲线”等知识的学习中将多次感悟.从功能上看，这一情境设置就是“解析几何本质揭示”的简介，是解析法思想的预告，对学生而言，在知识本质的理解上起到了先行组织之效.

2.情境设置应揭示整章认知系统的基本架构

实际教学中，部分学生在学习时体现出随心所欲的学习特质，学习过程杂乱无章，知识建构不成系统，导致学习内容易混易忘.究其原因，学生在开始阶段就没有形成整章内容的学习范式，没有用系统的眼光去进行学习，使得学习内容零散孤立，学习效果不佳.因此，在章节起始课的情境设置中，通过设计合适的情境来揭示整章认知系统的脉络，进而引导学生按照认知系统的基本架构去进行学习.

案例2苏教版必修5第3章起始课“不等关系”

图2

(展示图2:苏州的“东方之门”)(直观不等)

师：看到这幅图有什么直观感受呢？

生：感受到“会当凌绝顶，一览众楼小”，看到了楼房的高低不等.

(展示图3：身高体重真的一样吗？)(思考不等)

师：这两个武警身高、体重真的完全一样吗？

生：要是精确到毫米级，甚至纳米级，那么两个人的身高是不一样的.

图3

师：很好！说明在现实生活中“相等是相对的，不等是绝对的！”不等现象普遍存在于我们生活之中.

(展示图4：中国古代运用“不等”现象与杠杆原理制作的器械.)(运用不等)

图4

师：我们的祖先就已经智慧地将不等关系和杠杆原理运用到生活中去了，制作了方便于生活的器械(如捣谷用的“娄”和提水用的“桔槔”).

师评：上面三幅图，我们一起经历了“直观不等现象——思考不等关系——运用不等模型”，这就是我们学习“不等关系”的原因与过程，我们将以“建立不等关系(模型)——研究不等模型——运用不等模型”为线索进行整章的学习.

上述情境设置中蕴含着研究问题与数学学习的基本方向，即从实际情境中抽象出数学模型，通过思考和研究模型后，进而应用模型的思维过程.很显然，情境的目标指向是整章学习方向的引导，是整章学习过程的缩影，旨在帮学生建构出整章认知系统的基本脉络，为学生在后面学习中进行有目标、有意义的学习提供了基础与保证.

3.情境设置应引领整章教学的目标立意

人教社章建跃教授认为：课堂教学要做到“低起点，高立意”，提高课堂教学立意的关键是提高思想性.对同一教学内容而言，选择不同的引入方式，学生所获得的目标立意将有所不同.适宜的目标立意才能促进学生有意义的数学学习，换言之，过低的目标立意不能促进学生的认知发展，过高的目标立意不能引发学生的认知共鸣.因此，应根据预期所要达到的目标立意，创设适当的情境，以保证整章教学定位基于学生的最近发展区和可能的目标区.

案例3：苏教版必修5第1章起始课“正弦定理”

情境设置1：在初中，我们着重从几何的角度来研究三角形的边角关系，随着我们不断学习新知识，还可从哪些角度来研究三角形的边角关系吗？

预期目标立意：研究三角形的基本视角(方向).

由此目标立意带来的数学活动是：

——向量作为一种数学工具，既有形的特征，又有数的意义，因此，我们可以用“向量”来研究三角形；

——学习了必修2“平面解析几何”后知道，可以用坐标法来研究几何问题，可通过用坐标法来研究“正弦定理”；

——回顾初中三角函数的定义，将一般的三角形转化为直角三角形来研究“正弦定理”；……

继而以此目标引领后续教学：在教学“余弦定理”时也可以从这些视角进行探究，更一般地，在研究平面几何问题，同样地可选择几何方法，向量方法，坐标方法等多维视角去研究.

情境设置2：三角形有3个角3条边，至少给定这6个元素中的几个可以确定一个三角形？

至少给定三个元素：

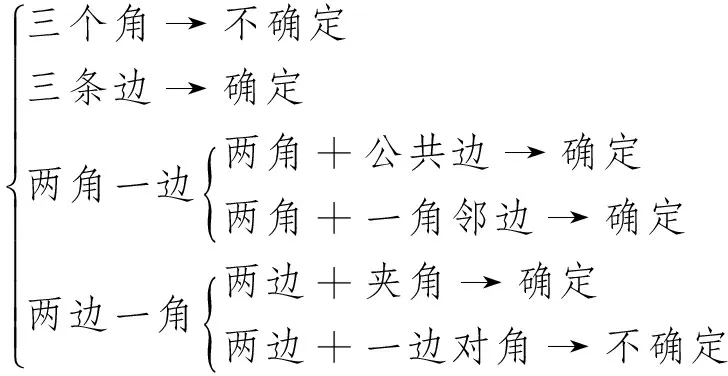
能“确定”三角形的这些条件的理论依据是什么？

预期目标立意：探寻能“确定”三角形的理论依据，发展学生的理性思维.

由此带来的数学活动：将上述条件先分类，以其中一组进行研究(如两角+一角邻边)，形成可操作的思维方式，再用类似的思维过程指导其他条件的研究.

不难看出，在起始课中的情境设置将引领着整章的目标立意走向，在后面的教学实施中若能以已有的目标立意为教学中心，学生的学习活动将是在同一建构系统中进行，帮助学生构建了研究数学问题的基本框架，以增强学生学习的自觉性、主动性，使学生的数学思考更有目的性、有序性和有效性，培养良好的数学思维习惯，目标达成的效度将大有提升，这样的教学更具思想性和数学味.

[1]章建跃.以整体观为指导提升问题的“启发度”[J].中小学数学(高中版)，2014，12：封底.

[2]章建跃.发挥数学的内在力量为学生谋取长期利益[J].数学通报，2013，2:1-6.