股票市场与黄金市场的波动溢出效应——基于沪深港股票市场和世界黄金市场数据

李双琦 朱 沙



股票市场与黄金市场的波动溢出效应
——基于沪深港股票市场和世界黄金市场数据

李双琦 朱 沙

（重庆工商大学财政金融学院，重庆 400067）

通过把世界黄金现货市场抽象成国际金融市场，用三元GARCH-BEKK（1，1）模型研究中国股票市场与香港股票市场及国际金融市场的波动溢出效应，进一步用三元DCC-GARCH（1，1）模型的动态相关系数刻画波动溢出效应的程度，从而将三者的波动溢出效应的定性分析和定量分析结合起来，结果发现沪深股票市场与香港股票市场、世界黄金现货市场存在双向波动溢出效应，香港股票市场与世界黄金现货市场不存在波动溢出效应，进而对完善我国金融市场且为投资者的投资提供借鉴。

股票市场；黄金市场；波动溢出；GARCH-BEKK；DCC-GARCH

一、引 言

为了适应资本市场发展的新形势，2005年9月4日，证监会发布了《上市公司股权分置改革管理办法》。由此，我国的股权分置改革进入了正式实施阶段，股票市场的流通性也增强了。于是，作为中国金融市场缩影的股票市场，与其他金融市场的联系逐渐加强，不再是一个相对独立的市场。2007年8月美国次贷危机引发的金融危机席卷全球，并波及到中国金融市场，而其影响的程度是由中国金融市场与国外波动溢出效应决定的。2014年11月17日，作为中国证券市场多层次、国际化发展重要举措的沪港通开始实施，沪深股票与香港股票关联性的变化，以及沪深股市与香港股市、国外金融市场的波动呈现的变化，对我国证券市场的稳定和健康发展都有深刻影响。厘清中国金融市场与其他金融市场之间的波动溢出效应，对处在经济全球化、利率市场化和人民币国际化进程中的中国，具有重要的理论与实践意义。

二、文献综述

金融时间序列作为高频时间数据，金融变量的时间序列通常存在条件异方差，在研究其波动时，最常用的是ARCH模型和GARCH模型。但在研究金融变量相关性时，由于一元GARCH模型存在短板，大量学者便尝试用多元GARCH模型来解决这一问题，从此多元GARCH模型出现多种形式：Bollerslev、Engel和Wooldridge（1998）提出了VECH模型；Engle R.F. and K.F. Kroner（1995）提出了BEKK模型；Bollerslev（1990）提出了CCC-GARCH模型；Engle R. F.和Sheppard（2002）为解决高频金融数据为常相关系数的不合理假定，在CCC-GARCH的基础上提出了DCC-GARCH模型。自Ross（1990）提出“波动溢出效应”的定义（一个市场的波动不仅对自身未来波动有影响，还可能对其他市场未来的波动产生影响）以来，众多国内外学者对各种不同金融市场之间的波动溢出效应做出了实证研究。

Dajcman、Silvo、Festic、Mejra（2012）[1]采用DCC-GARCH模型研究了斯洛文尼亚和其他国家（英国、德国、法国、澳大利、匈牙利和捷克）股票市场之间的波动溢出性。结果表明，斯洛文尼亚与这些国家之间存在显著的波动溢出效应。Tan Bee Huen、Arsad、Zainudin、Ooi Po Chun（2014）[2]利用GARCH-BEKK模型对2个发展中国家（马来西亚和中国）与2个发达国家（日本和美国）股票市场波动溢出效应进行的实证研究表明，发展中国家的股票市场与发达国家的股票市场存在双向溢出效应。龚朴、李梦玄（2008）[3]采用基于加权CCF的方差Granger因果检验方法，分析了上证指数、恒生指数收益序列的波动溢出效应，并通过BEKK模型对两序列间的时变相关性进行了实证，结果表明两股市之间不存在显著的波动溢出效应；尽管两股市的联系和联动性相对较弱，但有逐渐增大的趋势。董秀良、吴仁水（2008）[4]采用DCC-GARCH模型对我国沪深A、B股市场之间相关性的研究表明，沪深两市A、B股之间的相关系数总体为正，并具有明显的时变特征，而且沪深A、B市场之间的一体化程度正日趋增强，不过在处于相对高位之后并没有呈现出进一步提高趋势，股市场动态相关系数还相对低，市场分割特征仍然明显。董秀良、曹凤岐（2009）[5]采用多元GARCH-BEKK模型，以美国、日本、香港和我国沪市作为研究对象，对国内外股市波动溢出关系进行的研究发现，只有香港股市对沪市具有显著的波动溢出，美、日股市对沪市的波动溢出则不显著，但由于美、日股市波动可以借助对香港股市波动的影响间接地引起我国沪市的波动。姚琼（2012）[6]以沪深港三地股票市场指数数据为样本，通过构建三元GJR-GARCH- DCC模型对沪深港股市之间的联动效应进行的实证分析表明，沪深港股市之间存在明显的联动性，股权分置改革之后，中国内地股市更加国际化，市场之间的关系存在非对称性，沪市在三个市场之间已经起到了主导作用，市场间的动态相关性呈现增加的趋势。刘冠国（2013）[7]李永涛以上海黄金交易所的黄金现货AU9995和上证指数为对象，通过建立GARCH-BEKK模型进行的实证研究发现，两个市场收益率之间存在显著的双向波动溢出效应。

综上所述，国外学者的研究涉及中国股票市场较少，而国内学者的研究大多集中在国内或国外金融市场，对中外股市波动相关关系的研究不多。随着“沪港通”的正式实施，中国大陆股票市场与香港股票市场之间乃至世界金融市场的波动溢出性逐渐成为热点，也为本文的研究提供了方向。

三、实证分析

（一）数据的处理

本文选取沪深300指数（HS300）、香港恒生指数（HIS）、世界黄金现货指数（GGP）的收盘价，并以其收益率作为研究对象，样本区间为2007年7月16日—2015年7月16日。选HS300指数而不单独选取上证指数是因为“沪港通”的正式实施表面上对沪市影响更大，但大量学者的研究表明深沪两市具有高度联动性，HS300作为跨市场指数能够反映沪深市场整体走势，从而代表中国内地股票市场的整体情况。由于三个指数所在市场交易日期上有差异，为了各交易市场数据的同步性，删除各市场间不一致的交易数据，保留交易日期相同的数据。在计算指数收益率的时候采用来计算相应指数日收益率，其中为股票指数在该交易日的日收益率，与分别表示该交易日的收盘指数和前一个交易日的收盘指数，每个股指数得到的收益率序列包含1 895个交易数据，所有数据均来自于Wind数据库。本文数据描述和检验通过Eviews 7.0实现，GARCH-BEKK（1，1）和DCC-GARCH（1，1）模型的极大似然估计法的参数估计、检验及绘图通过Winrats8.0编程实现。

（二）数据的描述性统计

通过Eviews 7.0对沪深300指数（HS300）、香港恒生指数（HIS）、世界黄金现货指数（GGP）的收益率XHS300、XHSI、XGGP进行统计可得：其均值分别为4.00E-05、4.18E-05、0.000 287，标准差分别为0.019 254、0.017 055、0.012 935，可以看出恒生指数的收益率相对较大，沪深300指数收益率波动相对较大；其偏度分别为-0.266 143、0.001 019、0.202 114，峰度分别为5.586 274、11.583 48、8.973 868，J-B统计量分别为550.281 3、5 814.274、2 829.202，说明收益率序列均服从尖峰厚尾且左拖尾分布，而非正态分布。通过观察XHS300、XHSI、XGGP的时序图可以发现均存在群聚波动现象。

（三）收益率的假设检验

为了避免出现伪回归现象，本文采用ADF检验对XHS300、XHSI、XGGP数据的平稳性进行了检验，ADF统计量的值分别为-42.175 74、-44.754 39、-42.889 51均小于5%显著性水平下的临界值-2.862 864，于是拒绝“存在一个单位根”的原假设，也即是说XHS300、XHSI、XGGP均为平稳时间序列。

从XHS300、XHSI、XGGP自相关图和偏自相关图可看出，三个收益率均存在序列相关性，结合AIC准则和SC准则的值最小原则对三个时间序列做最小二乘估计，选择最佳滞后期分别为6、8、16。

表1 AR模型参数估计

AR参数估计t-statisticP-value XHS300=-0.065 32AR(6) + ε1-2.835 4490.004 6 XHSI=0.051 193AR(8) + ε22.215 4610.026 8 XGGP=-0.072 549AR(16) + ε3-3.154 0690.001 6

从相伴概率可以看出，在5%显著性水平下，其参数估计均是显著的。先分别对残差1、2、3做序列相关检验（LM检验），其Obs*R-squared的值分别为4.121 878、1.805 579、0.000 000，其相伴概率分别为0.127 3、0.405 4、1.000 0均大于0.05，即在5%显著性水平下，三个自回归方程不存在序列相关。然后分别对残差1、2、3做ARCH效应检验，其Obs*R-squared的值分别为45.654 42、307.055 4、23.807 51，其相伴概率均为0.000 0均小于0.05，即在5%显著性水平下，三个自回归方程均存在ARCH效应。

四、模型实证分析

（一）GARCH-BEKK（1，1）模型

1．GARCH-BEKK（1，1）模型构建

本文采用Engle R. F. and K. F. Kroner1995年提出的GARCH-BEKK模型的三元BEKK（1，1）形式，其优点是可以在很弱的条件下保证协方差矩阵的正定性且需要估计的参数较少，因此在分析实际问题时，该模型是一种简便的表达式。假设有A、B、C两个市场，其三元BEKK（1，l）模型的形式如下：

（2）

其中，X为金融变量的收益率，（）为收益率的滞后期值。H为误差项ε的3×3阶条件方差及协方差矩阵。是3阶下三角参数矩阵，和是3×3阶参数矩阵，表示条件方差方程的常数项部分，和分别代表ARCH项、GARCH项的系数。

本文利用向量VAR模型建立均值方程，通过AIC准则SC准则并结合LM统计量确定最优滞后阶数，经过试算比较发现：沪深股市、香港股市、世界现货黄金市场适合采用均值方程右边VAR（1）的形式，滞后项分别为AR（6）、AR（19）、AR（16）；运用极大似然估计法对上述建立的向量形式的BEKK（1，1）形式的方差方程进行估计方差方程的参数估计（见表2）。

表2 GARCH-BEKK（1，1）参数估计

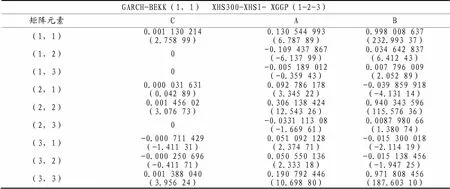
GARCH-BEKK（1，1） XHS300-XHSI- XGGP（1-2-3） 矩阵元素CAB （1，1）0.001 130 214（2.758 99）0.130 544 993（6.787 89）0.998 008 637（232.993 37） （1，2）0-0.109 437 867（-6.137 99）0.034 642 837（6.412 43） （1，3）0-0.005 189 012（-0.359 43）0.007 796 009（2.052 89） （2，1）0.000 031 631（0.042 89）0.092 786 178（3.345 22）-0.039 859 918（-4.131 14） （2，2）0.001 456 02（3.076 73）0.306 138 424（12.543 26）0.940 343 596（115.576 36） （2，3）0-0.0331 113 08（-1.669 61）0.0087 980 66（1.380 74） （3，1）-0.000 711 429（-1.411 31）0.051 092 128（2.374 71）-0.015 300 018（-2.114 19） （3，2）-0.000 250 696（-0.411 71）0.050 550 136（2.333 18）-0.015 138 456（-1.947 25） （3，3）0.001 388 040（3.956 24）0.190 792 446（10.698 80）0.971 808 456（187.603 10）

2．沪深股市、香港股市、世界现货黄金市场波动溢出

从表3看出：对参数未施加任何限制的BEKK模型的估计结果中方差方程ARCH项系数矩阵和GARCH项系数矩阵的对角元素、、、、、，在5%显著性水平下显著不为0，说明每个市场的波动均受自身以往波动的影响，波动聚类性显著。

市场间波动溢出的检验结果表明：对于沪深股市和香港股市来说，三个Wald检验的相伴概率均小于0.05，说明在5%显著性水平下拒绝原假设，即沪深股市对香港股市存在双向波动溢出；对于沪深股市和世界现货黄金市场来说，三个Wald检验的相伴概率也均小于0.05，说明在5%显著性水平下，沪深股市与世界现货黄金市场之间存在双向波动溢出。对于香港股市与世界现货黄金市场来说，三个Wald检验的相伴概率均大于0.05，说明在5%显著性水平下不能拒绝原假设，即香港股市与世界现货黄金市场之间不存在波动溢出。

综上可见，沪深股市的波动与香港股市、世界黄金现货市场均存在双向波动溢出，并受自身前期波动的显著影响。这可能是由于国内一系列金融市场改革措施的实施，加强了中国金融市场与国际金融市场的联动性。2005年9月4日，证监会发布《上市公司股权分置改革管理办法》，我国的股权分置改革进入实施阶段，中国股票市场流通性变得更强，中国股票市场作为中国金融市场的缩影不再是一个相对独立的市场，与其他金融市场的联系逐渐加强。2007年8月美国“次贷”危机引发的金融危机席卷全球，中国金融市场也遭受了金融危机引发的经济疲软所带来的冲击。2014年11月17日沪港通开始实施，这是中国为适应资本市场发展的新形势，在经济全球化、利率市场化和人民币国际化背景下，提出开放金融市场的新举措。香港作为全球重要的金融中心，香港黄金市场也作为全球几大黄金市场之一，香港股市与世界现货黄金市场之间不存在波动溢出，初步判断这可能是由于香港股票市场与香港黄金市场的波动溢出更加明显，而与世界黄金市场的波动溢出不显著，香港股票市场与世界黄金市场的波动溢出是一种间接影响关系的信号，比如香港股票市场与世界黄金市场的波动溢出效应是借助对其它金融市场的影响而产生的，并非两个市场之间波动毫无影响，只是在确定的显著水平下不明显而已。

表3 Wald检验

原假设Wald A（1，2）=B（1，2）=A（2，1）=B（2，1）=0A（1，2）=B（1，2）=0A（2，1）=B（2，1）=0F（4，*）=11.449 93 [0.000 000 00] F（2，*）=22.772 50 [0.000 000 00] F（2，*）=8.766 59 [0.000 155 85] A（1，3）=B（1，3）=A（3，1）=B（3，1）=0A（1，3）=B（1，3）=0A（3，1）=B（3，1）=0F（4，*）=3.679 31 [0.005 325 12] F（2，*）=4.392 38 [0.012 371 30] F（2，*）=3.104 90 [0.044 829 06] A（2，3）=B（2，3）= A（3，2）=B（3，2）=0A（2，3）=B（2，3）=0A（3，2）=B（3，2）=0F（4，*）=1.791 75 [0.127 321 51] F（2，*）=1.398 00 [0.247 090 85] F（2，*）=2.951 56 [0.052 258 27] A（1，1）=B（1，1）=0A（2，2）=B（2，2）=0A（3，3）=B（3，3）=0F（2，*）=990 41.736 27 [0.000 000 00] F（2，*）=79.145 57 [0.000 000 00] F（2，*）=484 57.546 19 [0.000 000 00]

（二）DCC-GARCH（1，1）模型

1．DCC-GARCH（1，1）模型构建

DCC-GARCH模型，即动态条件相关多变量广义自回归异方差模型，与其他模型比相比最大的特点是相关系数随时间变化而变化。DCC-GACH模型通常通过两步来估计：第一步对各变量做GARCH（1，1）模型，用获得的条件方差去除残差得到标准化残差，第二步以此标准化残差利用极大似然估计法估计动态相关结构的参数。在Engle和Sheppard（2002）提出的二元DCC-GARCH模型基础上，本文采用三元DCC-GARCH（1，1）模型，动态相关设定形式为：

表4 DCC-GARCH（1，1）模型的参数估计

CABDCC （1）2.348 36e-006（2.755 46）0.053 45（7.241 24）0.940 51（115.455 39）0.007 88（1.437 44） （2）2.491 76e-006（3.621 41）0.071 05（7.490 55）0.917 30（85.067 56）0.931 93（16.232 32） （3）2.641 74e-006（3.212 73）0.058 66（6.026 50）0.925 92（73.869 87）

基于DCC（1，1）-GARCH（1，1）模型，得到沪深股市、香港股市、世界现货黄金市场市场收益率的动态异方差（见表4）。由表3可知：（）表示ARCH项系数，（）表示GARCH项系数，（）+（）<1符合约束条件，（）+（）表示收益率波动的持续性，由此可见三个市场波动的持续性都很强；（）体现了滞后一期的标准化残差乘积对动态相关系数的影响，其含义为现有信息对下一期波动性的影响程度，数值越高说明该股市对新信息的敏感度越高，（）在（0.05，0.08）区间范围之内，表明三个市场收益率本期的动态异方差受其前期均值残差平方的影响较小；（）接近于1，表明三个市场收益率的本期的动态异方差主要依赖与其前期的动态异方差。此外，整个DCC 模型的参数分别为ARCH项系数DCC（1）为0.007 88，GARCH项系数DCC（2）为0.931 93，整体上看对新信息的敏感程度并不强，但在波动的持续性上，DCC（1）+ DCC（2）= 0.939 81表现出较高的波动持续性。

2．动态相关系数分析

从图1到图3（图见下页）的动态相关系数路径图可以得出以下几个结论。

第一，HS300收益率与HSI收益率以及HS300收益率与GGP收益率之间的动态相关系数的时变趋势基本保持一致；HSI收益率与GGP收益率的动态相关系数大体趋势也基本一致，只是波动幅度和方向在部分时段发生了扭曲。

第二，HS300收益率与HSI收益率之间表现出较高的联动性，在“沪港通”实施前联动性也较稳定，动态相关系数一直在（0.3，0.7）的区间内波动，沪港通”实施后HS300收益率与HSI收益率动态相关系数成下降趋势，可能源于两个市场结构差异逐渐显现，而且中国股票市场依旧没有摆脱“政策市”的影响，股票市场依旧不健全，投资者的投机心理对市场的影响较大；HS300收益率与GGP收益率的动态相关系数在（-0.05，0.1）区间范围内波动，甚至出现波动聚集现象，但其联动性较低；HSI收益率与GGP收益率的动态相关系数将样本分成3个区间段：2007年7月—2011年9月、2011年9月—2014年9月、2014年7月—2015年7月，其波动区间分别为（0，0.1）（-0.05，0）（0，0.05），其相关性程度较低，从另一个角度看，构建不同市场间的投资组合可以达到分散风险的作用，因此不可忽低相关和负相关的波动的市场。

第三，虽然沪深股票市场与香港股票市场、世界黄金市场之间的联动性不算太高，但是沪深股票市场与香港股票市场联动性远远高于强于沪深股票市场与世界黄金市场之间的联动性。

动态条件相关系数是描述金融市场之间的走势趋同程度高低的重要指标，动态条件相关系数高说明市场之间走势趋同程度大，市场一体化高，反之说明二者市场走势有较大的偏离，存在市场分割效应。由上述分析可知：中国金融市场没有表现出与其他金融市场高度相关，一方面金融监管部门的政策影响依然较大，投资者主要以投机为主，没有形成中长期投资的成长理念；另一方面，汇率也是不可忽略的因素，我国自2005年汇率改革以来，人民币一直保持着升值的趋势，国内人在投资国际金融资产时需要承担一定的汇率风险，造成了一定程度市场分割。

图1 HS300收益率与HSI收益率的动态相关系数

根据现代社会对于慈善的判定标准，义演本身作为一种文艺形式，在无形之中就起到了教育和促进文化传播的作用。上文中已经提到，民国初年，一些从西方留学归来的知识分子将具有西方文化特征的戏剧和话剧等表演形式带回中国，经过戏剧改良产生了文明戏等近代剧种，带有字幕的电影在近代都市社会也被频繁地搬演到慈善义演的舞台。现代文明戏剧的推广和播放带有字幕的电影等文艺形式，推广了白话文，传播了平等文明的观念，这一切活动都具有传播现代教育理念、发展科学文化、使社会文明开化的功能，所以，带有近代文明特征的义演活动直接或间接地推动了近代社会教育和文化的发展，构成了慈善的第二重效益。

图2 HS300收益率与GGP收益率的动态相关系数

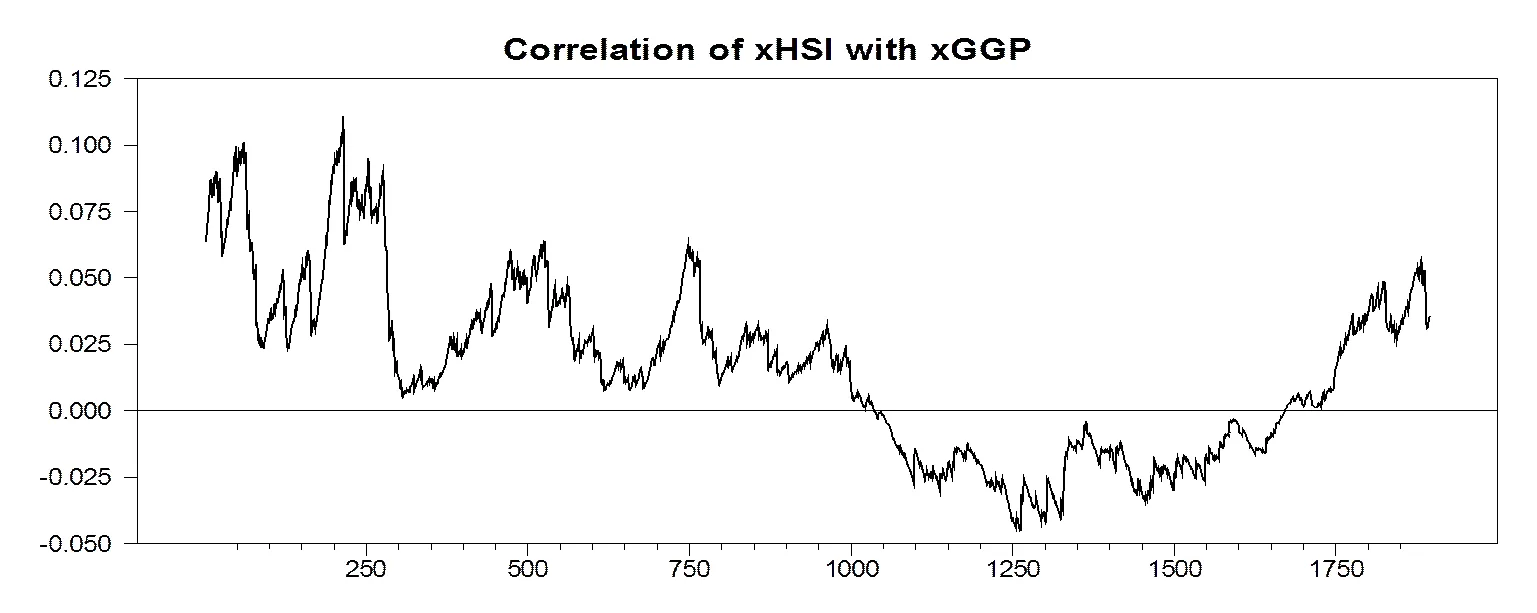
图3 HSI收益率与GGP收益率的动态相关系数

五、结 论

本文通过把世界黄金现货市场抽象成国际金融市场，用三元GARCH-BEKK（1，1）模型研究中国沪深股票市场与香港股票市场及国际金融的波动溢出效应，结果沪深股票市场与香港股票市场、世界黄金现货市场存在双向波动溢出效应，香港股票市场与世界黄金现货市场不存在波动溢出效应。进一步用三元DCC-GARCH（1，1）模型的时变相关系数刻画波动溢出效应的程度，沪深股票市场与香港股票市场、世界黄金市场之间的联动性不算太高，但是沪深股票市场与香港股票市场联动性远远高于强于沪深股票市场数与世界黄金市场之间的联动性；香港股票市场与世界黄金市场的动态相关系数处于低水平，甚至出现负相关的波动形态。

随着“沪港通”正式实施，经济全球化、利率市场化和人民币国际化进程不断深入，资本双向流动会更加频繁。此外，中国金融市场对外开放程度提高，中国国内金融市场与国际金融市场的波动溢出可能会进一步显著起来。基于以上实证研究结果，波动溢出效应和动态相关性，可以得到以下启示。

第一，我国金融监管部门应该逐步转变政府职能，应当进一步加强金融市场竞争机制，逐步减少政策干预，逐步增加不同种类和风险程度的金融衍生工具，逐步开放资本市场以适应经济全球化的必然趋势，加强国际金融合作应对全球化金融危机冲击，培育健康的国内、国际金融环境。

第三，随着我国金融市场全球化趋势的加强，投资者要充分考虑不同金融市场的联动性和动态相关性，在进行定性和定量分析基础上，可利用不同的低波动溢出效应和负相关性市场进行跨市场资产以达到资产组合的有效配置从而制定更理性的量化投资策略，分散投资风险，减少投资策略不当而造成不必要的损失。

[1] Dajcman, Silvo, Festic,Mejra. Interdependence between the Slovenian and European Stock Markets-A DCC-GARCH Analysis[J],Ekonomska Istrazivanja/Economic Research, 2012(2)：379-395.

[2] Tan Bee Huen, Arsad, Zainudin, Ooi Po Chun .Spillovers Among Regional And International Stock Markets[J].AIP Conference Proceedings. 2014, Vol. 1605: 828-833.

[3] 龚朴，李梦玄.沪港股市的波动溢出和时变相关性研究[J].管理学报，2008（1）：96-100.

[4] 董秀良，吴仁水.基于DCC-MARCH模型的中国A、B股市场相关性及其解释[J].中国软科学，2008（7）：125-133.

[5] 董秀良，曹凤岐.国内外股市波动溢出效应—基于多元GARCH模型的实证研究[J].数理统计与管理，2009（1）：1091-1099.

[6] 姚琼.基于GJR-GARCH-DCC模型的沪深港股市的联动性研究[J].中南财经政法大学研究生学报，2012（6）：85-93.

[7] 刘冠国.中国黄金市场和股票市场之间波动溢出效应研究[J].理论学刊，2013（11）：47-51.

[8] 张心培，王峰.“沪港通”波动溢出效应研究——基于DCC-MVGARCH模型的实证分析[J].河北金融，2015（5）：20-23.

（责任编辑：于开红）

朱 沙（1979-），男，四川成都人，重庆工商大学财政金融学院副教授，博士，主要研究金融市场。

The Volatility Spillover Effect between Stock Market and Gold Market Based on the Data of Shanghai, Shenzhen and Hong Kong Stock Market and Global Gold Market

LI Shuangqi ZHU Sha

(School of Finance, Chongqing Technology and Business University, Chongqing 400067)

This paper, abstracting global spot gold market from the international financial market, investigated the volatility spillover effect of Chinese stock market, the Hong Kong stock market and financial market by ternary GARCH-BEKK (1, 1) model. And the author chooses dynamic correlation coefficient of ternary DCC-GARCH (1, 1) with the degree of correlation model to portray the degree of volatility spillover effect so that combining qualitative analysis of volatility spillover effect among the three markets and quantitative analysis can be made. The result shows that there exists bidirectional volatility spillover effect between the Shanghai stock market, Shenzhen stock market and the Hong Kong stock market as well as global gold spot market. In addition, there does not exist volatility spillover effect between Hong Kong stock market and global gold spot market. Finally, this paper aims at improving the Chinese financial market and providing reference for investors.

Stock market; gold market; volatility spillover; GARCH-BEKK; DCC-GARCH

F830.9；F222.3

A

1009-8135（2016）02-0073-07

2015-12-01

李双琦（1990-），男，湖北武汉人，重庆工商大学金融学2014级硕士研究生，主要研究投资学。

2015年重庆市教委科技项目“基于粒子群的金融投资组合问题研究”（KJ1500618）阶段性成果