基于影长的数学建模分析及其在地理定位方面的应用～以2015年全国大学生数学建模竞赛的数据为依托

2016-08-22李昂

地球 2016年4期

关键词：直杆影长经度

■李昂

（吉林大学地球科学学院吉林长春130021）

基于影长的数学建模分析及其在地理定位方面的应用～以2015年全国大学生数学建模竞赛的数据为依托

■李昂

（吉林大学地球科学学院吉林长春130021）

在地质工作乃至其他各行各业，定位技术都有着广泛的应用。现有的定位方式以卫星定位为主要技术手段，通过GPS接收装置接收位置信息，完成所在经纬度和其他位置信息的采取。本文则在卫星定位之外，以天体运行的轨道内在规律为理论基础，借助太阳光照射角度及其产生的影子长度，通过枚举法，最小方差模型，以及二次拟合等方法对于数据进行数学处理，最终得出定位模型。

太阳高度角影长最小方差枚举经纬度

1　基于已知时间地点的基础上进行影长的预测

在建立地理定位模型之前，本文首先做了一个逆推的模型，即在地点和时间已知的情况下计算影长，为后续研究做理论基础。

通过前人的研究，我们已知太阳照射地面所形成的角度，即太阳高度角符合一个基本的数学关系。

太阳高度角模型

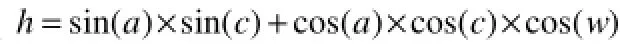
其中a为纬度，c为赤纬，w为太阳时角。

1.1对于上述公式的分析和计算

（1）赤纬δ计算方法：

sinδ=0.39795cos[0.98563(N～173)]式中N为日数，自每年1月1日开始计算。

（2）真太阳时：是以真太阳视圆面中心的时角来计量的，它的起算点是真太阳上中天。由于在中国境内普遍使用的时间是北京时间，即东经120度位置处的真太阳时。由于地球自转一圈时间为24 h,自转角度为360度，我们可以得出地球每小时的自转角度为15度。由此，我们可以计算出经度为b的地区的真太阳时。

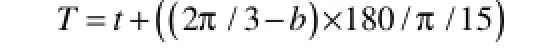
根据太阳时角（ω）计算公式

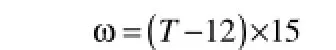
可以得出太阳时角ω的值。

根据以上数值，我们可以较容易的计算出太阳高度角h

1.2考虑大气折射影响，对太阳高度角进行修正

参考斯涅尔定律，得修正后的太阳高度角

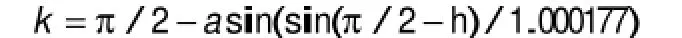
为了印证上述模型，进行模型演绎，即预测2015年10月22日北京时间9:00～15:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆的太阳影子长度的变化曲线。将影长变化模型在MATLAB中编程实现，时间从9点到15点，步长取0.001。

上述预测结论在全国大学生数学建模竞赛云南总审核阶段结论得到印证。

2　反演上述模型，在已知影长及时刻的基础上，获得地理位置信息

要根据物体影子顶点的坐标数据确定投射影子的直杆所处的地点，即找到直杆所在的经纬度，实际上就是对第一章内容的反推，包括以下经度获取和纬度获取两个方面。

（1）计算经度：固定直杆在太阳光照射下产生的影长从上午到正午再到下午是先变短后变长的，与二次函数曲线吻合，所以我们采用二次拟合法。建立物体影长与时间的拟合曲线，通过微分法找到最短影长所对应的时刻，即为当地时间正午。同时根据当地时间正午所对应的北京时间和北京的经度，通过时差转换，即可得当地的经度值。

（2）计算纬度：采用近似逼近法求纬度。现已知当地的经度，将纬度从～90度到90度，取步长为1°遍历。在每次遍历下，假设当地某一直杆L,可以利用问题1中所建立的模型求出其在已知经度下21个时刻所对应的影长。在21个时刻下直杆L影长与题目所给数据影长二者比值的方差最小值所对应的纬度即为当地的纬度，此过程由MATLAB7.8编程实现。

2.1经度的求解

二次拟合就是把已知的数据用二次曲线近似的表示出来，由于影长随太阳高度及方位的变化先变长再变短再变长，因此可以采用二次曲线进行拟合。

（1）首先我们把影子长度的数据导入矩阵中(以2015年全国大学生数学建模竞赛的数据为例，长度由坐标投影方法获得)。

得=[1.1496 1.1822 1.2153 1.2491 1.2832 1.3180 1.3534 1.3894 1.4262 1.4634 1.5015 1.5402 1.5799 1.6201 1.6613 1.7033 1.7462 1.7901 1.8350 1.8809 1.9279]

（2）数据源信息是，时间是从14点42分一直到15点42分，每隔3分钟记录一次。本文用MATLAB对时间和影长进行二次拟合，得到拟合系数A。

A=[0.1489～3.7519 24.1275]

（3）利用系数A进行拟合，得到拟合曲线。