“圆”复习专题参考答案



“圆”复习专题参考答案

1.B【解析】∵四边形ABCD是圆O的内接四边形，∠A=70°，∴根据圆内接四边形对角互补的性质，得∠C=110°.

2.D【解析】容易发现BO，CO是三角形ABC的内角平分线，进而转化到三角形OBC和三角形ABC中利用三角形内角和思考.

3.A【解析】连接AO，BO，可得等边三角形ABO，从而问题转化为求等边三角形的高.

4.D【解析】由AC是弧的切线知∠CAO为直角，于是在直角三角形ACO中，分别求出该三角形面积再减去扇形的面积，可得阴影部分面积.

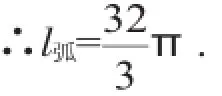
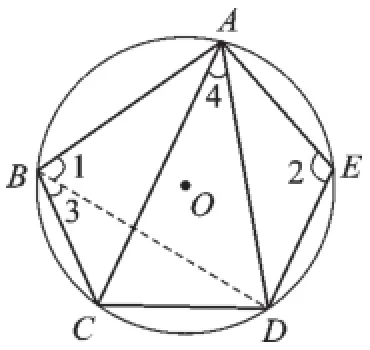
第7题图

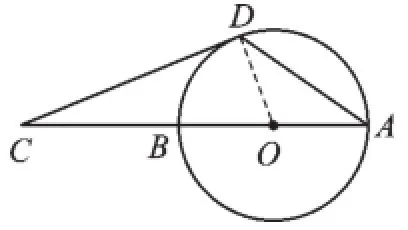
第8题图

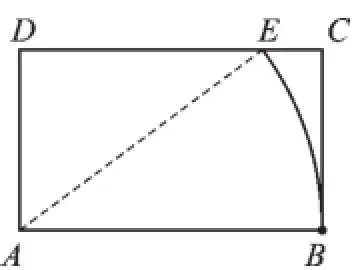
7.215°【解析】如图，连接BD，

∵∠1和∠2是圆内接四边形的对角，∴∠1+∠2=180°.

又∵∠3和∠4是同圆中同弧所对的圆周角，且∠4=35°，

∴∠3=∠4=35°.∴∠CBA+∠DEA=215°.

8.125°【解析】如图，连接OD，

∵CD与⊙O相切于点D，∴CD⊥OD.

∴∠CDO=90°.∵∠C=20°，∴∠COD=70°，∴∠A=35°.

∴∠CDA=180°-∠C-∠A=125°.

9.30°【解析】根据同弧所对圆周角相等，∠D=∠B=60°，进而在直角△AED中思考即可.

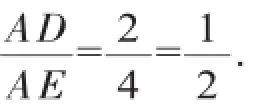
12.3＜r＜5【解析】如图，连接BD，

∵AB=4，AD=3，∴根据勾股定理，得BD=5.

∵AD＜AB＜BD，

第11题图

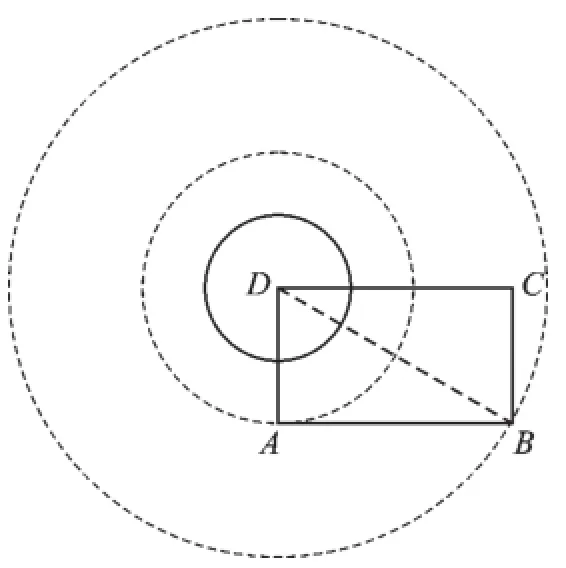
第12题图

∴当AD＜r＜BD时，点A、B、C中至少有一个点在圆内，且至少有一个点在圆外.

∴r的取值范围是3＜r＜5.

13.EC与FD的数量关系是：EC=FD.

证明：连接OA，OB，

∵OA，OB是⊙O的半径，∴OA=OB，∴∠OBA=∠OAB.

又∵AE=BF，∴△OAE≌△OBF，∴OE=OF，∴EC=FD.

14.（1）正确作出图形.

由题意可知，CD=4 cm.设半径为x cm，则OD=（x-4）cm.

在Rt△BOD中，由勾股定理得OD2+BD2=OB2，

∴（x-4）2+82=x2，∴x=10.

即这个圆形截面的半径为10 cm.

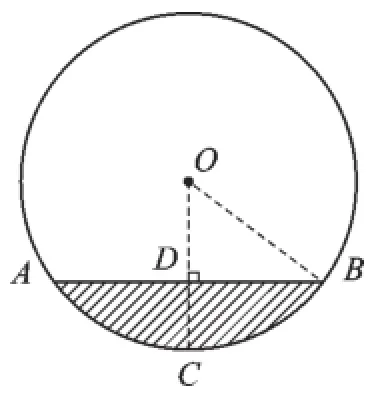
第14题图

这个零件的外侧面积=12π·8=96π，

所以这个零件的表面积为：36π+96π+60π=192π（cm2）.

16.△GBD是等边三角形.

证明：∵CF∥AD，∴∠BGD=∠F.

∵△ABC等边三角形，∴∠BAC=∠ACB=60°.

∵∠F=∠BAC=60°，∠BDG=∠ACB=60°，

∴∠BGD=∠BDG=60°.

∴△GBD是等边三角形.

17.（1）证明：连接OA.∵DA平分∠BDE，∴∠BDA=∠EDA.

∵OA=OD，∴∠ODA=∠OAD.

∴∠OAD=∠EDA.∴OA∥CE.

∵AE⊥DE，∴∠AED=90°，∴∠OAE=90°.

∴AE⊥OA.∴AE是⊙O的切线.

（2）∵BD是直径，∴∠BCD=∠BAD=90°.

∵∠DBC=30°，∴∠BDC=60°，

∴∠BDE=120°.

∵DA平分∠BDE，∴∠BDA=∠EDA=60°.

∴∠ABD=∠EAD=30°.

在Rt△AED中，∠AED=90°，∠EAD=30°，∴AD=2DE.

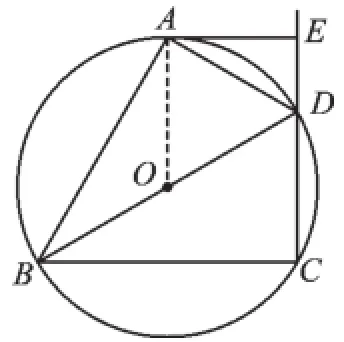
第17题图

在Rt△ABD中，∠BAD=90°，∠ABD=30°，∴BD=2AD=4DE.

∵DE的长是1 cm，∴BD的长是4 cm.

18.（1）连接BD交GF于点M，则点M为所求；

α角的度数为90°；

（2）点E位于边AB的中点处，△EFG的面积取得最小值.理由如下：

设正方形ABCD边长为a，AE=x，则BE=a-x，可得AG=a-x，

则在Rt△AGE中，GE2=x2+（a-x）2=2x2-2ax+a2.

而在△AGE和△BEF中，

AG=BE，∠A=∠B，AE=BF，

∴△AGE≌△BEF（SAS）

∴GE=FE，∠AGE=∠BEF，

又∠AGE+∠AEG=90°，

∴∠BEF+∠AEG=90°，

∴∠GEF=90°.

∴△EFG是等腰直角三角形.

即当点E位于边AB的中点处，△EFG的面积取得最小值.

（3）△EFG的外接圆与直线CD相交.

由（2）中可知△EFG是等腰直角三角形.

如图，取GF中点M，连接ME，则有MG=ME=MF.

以ME为半径，点M为圆心的⊙M是△EFG的外接圆.

由DG=BF，且M为GF中点，

则DG、BF是关于点M成中心对称，即点M为正方形的对称中心.

过点M作MH⊥AB于点H，反向延长MH交CD于点K，

根据中心对称性质有MH=MK，且MK⊥CD.

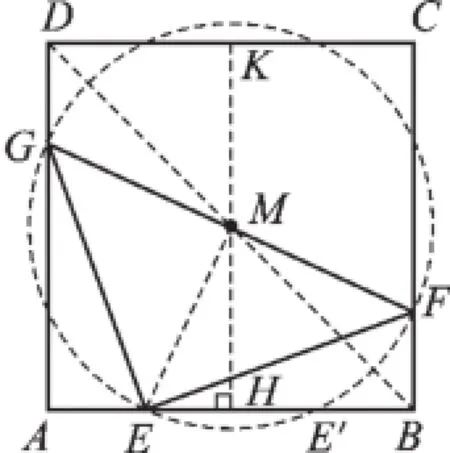
第18题图

所以，当点E运动到AB中点处时，与点H重合，⊙M与边AB相切，相应的也就与直线

根据中心对称性质，此时⊙M与直线CD的两个交点之间距离也为2.