“四边形”复习专题参考答案



“四边形”复习专题参考答案

1.B【解析】根据平行四边形判定条件，提供的4组条件中只有对角线互相平分可以判定平行四边形.

2.B【解析】由平行四边形性质，邻角互补，对边相等，可以确认只有选项B正确.

3.C【解析】由三角形中位线定理可知在P点的运动过程中，EF一定等于AR的一半，又由于AR的长不变，所以可做出正确的判断.

4.D【解析】这是考查多边形内角和的创新试题，由于裁去一个角存在不确定性，所以要分不同情形讨论.

5.D【解析】由题意可以发现特殊角30度角，从而得出含30°角的特殊直角三角形.

6.A【解析】连接FB.

∵四边形EFGB为正方形，∴∠FBA=∠BAC，∴FB∥AC，∴△ABC与△AFC是同底等高的三角形.∵2S△ABC=S正方形ABCD，S正方形ABCD=2×2=4，∴S=2.

7.4【解析】由正方形的对称性知对边中点所连直线、对角线所连直线，共4条对称轴.

8.5【解析】由条件先求出另一边长为4，则根据勾股定理可求出对角线为5.

9.32【解析】平分这个内角的对角线是较短的对角线，该对角线所对内角为60°，于是等边三角形就出现了，从而菱形边长为8 cm，于是周长为32 cm.

10.2【解析】根据正方形的对称性质，可知其中一个阴影部分是正方形的面积的四分之一，则两个阴影部分面积为一个正方形面积的一半.

11.10【解析】由平行四边形ABCD的性质得AD=BC，AB=CD，OB=OD，又因为周长为20 cm，所以AB+AD=10 cm.又因为OB=OD，OE⊥BD，由线段的垂直平分线的性质得：BE=ED，所以△ABE的周长为AB+AE+BE=AB+AD=10 cm.

12.5【解析】根据轴对称性质，取M关于AC的对称点M′，连接M′N交AC于点P，于是设法求出M′N即可.当然，还需要根据勾股定理先求出菱形的边长为5.

13.证明：∵四边形ABCD为平行四边形，∴∠B=∠D，AB=CD，BC=AD.

又∵E，F，G，H分别是▱ABCD的四边中点，

∴BE=DG，BF=DH，∴△BEF≌△DGH.

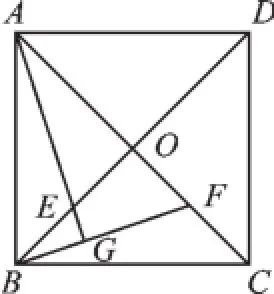
14.解：（1）△ABE≌△BCF，△AOE≌△BOF，△ABF≌△DEA；

（2）证明：②如右图，延长AE交BF于点G，

∵ABCD是正方形，∴AB=BC，∠BCF=∠ABE，

∵BE=CF，∴△ABE≌△BCF，∴∠CBF=∠BAE，

∵∠ABE+∠EBG+∠CBF=90°，∴∠ABE+∠EBG+∠BAE=90°，

∴∠AGB=90°，∴AE⊥BF.

15.解：（1）菱形图案水平方向对角线长为BD=2BO=2AB·cos∠ABO=10×cos30° ×2=30（cm），按题意，L=30+26×（231-1）=6 010（cm）.

（2）当d=20 cm时，设需x个菱形图案，则有：30+20×（x-1）=6 010，解得x=300，即需300个这样的菱形图案.

16.解：（1）如右图，射线OB为所求作的图形.

（2）方法一：∵OB平分∠MON，∴∠AOB=∠BOC.

∵AE∥ON，∴∠ABO=∠BOC.∴∠AOB=∠ABO，AO=AB.

∵AD⊥OB，∴BD=OD.

∵AB∥OC，所以四边形OABC是平行四边形.

∵AO=AB，所以四边形OABC是菱形.

方法二：同方法一，∠AOB=∠ABO，AO=AB.

∵AD⊥OB于点D，所以OD=DB，∠ADO=∠CDO=90°.

所以四边形OABC是平行四边形.

∵AO=AB（或AC⊥OB），所以四边形OABC是菱形.

17.正确.

说明如下：

方法一：设AC，BD交于O，∵AB=AD，BC=DC，AC=AC，

∴△ABC≌△ADC，∴∠BAC=∠DAC，AB=AD，∴AO⊥BD，

方法二：因为AB=AD，

所以点A在线段BD的中垂线上.

又因为CB=CD，所以点C在线段BD的中垂线上，

所以AC所在的直线是线段BD的中垂线，即BD⊥AC.

18.（1）由折叠可知，在Rt△ABC中，AC=2 cm，BC=4 cm，

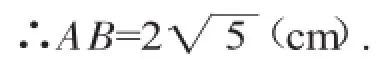
（2）图中黄金矩形有两个，分别是矩形BCDE，矩形MNDE.

矩形BCDE为黄金矩形的理由如下：

即矩形BCDE为黄金矩形.

即矩形MNDE为黄金矩形.

（3）由翻折知，AB=AD，∠BAQ=∠DAQ，

∵BQ∥AD，∴∠BQA=∠DAQ.∴∠BQA=∠BAQ.∴BA=BQ.∴AD=BQ.

∴四边形ADQB是平行四边形.（一组对边平行且相等的四边形是平行四边形）

∴平行四边形ADQB是菱形.（一组邻边相等的平行四边形为菱形）

方法一：（分别计算AQ，BD的平方，得到斜边的平方…）

∴围成的直角三角形斜边的平方为AQ2+BD2=80，斜边长

方法二：

由上面知道四边形ADQB是菱形.

如下图，平移对角线BD到QP的位置.

∴Rt△APQ中，AP2=AQ2+PQ2.∴AP2=AQ2+BD2.

∴AP为所求的直角三角形的斜边.

注，此法也可从菱形ADQB对角线分成的四个小直角三角形中思考突破.