如何捏住中考概率题的“七寸”

朱余进



如何捏住中考概率题的“七寸”

朱余进

俗话说的好“打蛇打七寸”.近年来学生在中考数学题中处理有关概率题时，尽管平时老师反复讲反复练，但一到考试还是状况百出.同学们的错题反复出现，历来是老师重视和值得探讨的一个课题，其原因不能简单地归咎于同学们粗心或学习不认真，解题过程中通常都要经过问题的识别、记忆、理解、激活背景观念、选择调整解题方法等步骤.同学们除了依赖原有的知识技能外，还和本身的心理品质和智力能力密不可分.

同学们出现错题有一些常见原因，如审题不清、概念模糊、思维跳跃、表达含糊、计算失误等，下面将2015年部分地区的中考试卷中的有关“概率与统计”的经典试题整理了一些，供同学们阅读参考.

例1（2015·威海）甲、乙两布袋装有红、白两种小球，两袋装球总数量相同，两种小球仅颜色不同.甲袋中，红球个数是白球个数的2倍；乙袋中，红球个数是白球个数的3倍，将乙袋中的球全部倒入甲袋，随机从甲袋中摸出一个球，摸出红球的概率是（）.

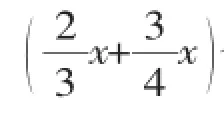
【正解分析】2倍关系中总数是3份，3倍关系中总数是4份，因此最小公倍数是12.

解：∵甲袋中，红球个数是白球个数的2倍，

∴设白球为4x，则红球为8x，

∴两种球共有12x个，

∵乙袋中，红球个数是白球个数的3倍，且两袋中球的数量相同，

∴红球为9x，白球为3x，

故选C.

例2（2015·常州）甲，乙，丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛，他们将通过抽签来决定比赛的出场顺序.

（1）求甲第一个出场的概率；

（2）求甲比乙先出场的概率.

【正解分析】（1）画树状图得出所有等可能的情况数，找出甲第一个出场的情况数，即可求出所求的概率；

（2）找出甲比乙先出场的情况数，即可求出所求的概率.

解：（1）画树状图如下：

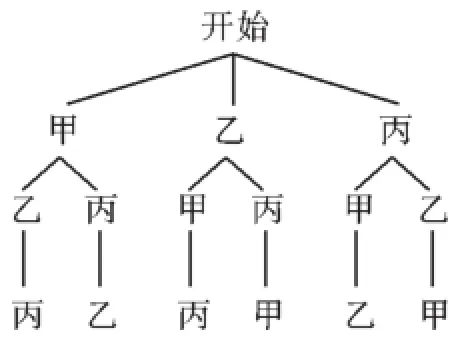
例3（2015·南通）为增强学生环保意识，某中学组织全校2 000名学生参加环保知识大赛，比赛成绩均为整数，从中抽取部分同学的成绩进行统计，并绘制成如图统计图.请根据图中提供的信息，解答下列问题：

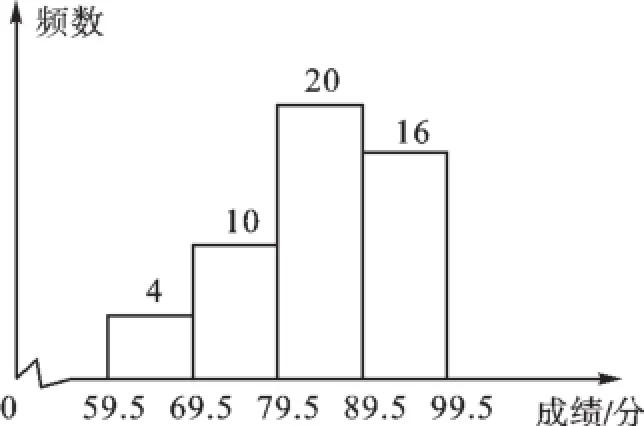
（1）若抽取的成绩用扇形图来描述，则表示“第三组（79.5～89.5）”的扇形的圆心角为______度；

（2）若成绩在90分以上（含90分）的同学可以获奖，请估计该校约有多少名同学获奖？

（3）某班准备从成绩最好的4名同学（男、女各2名）中随机选取2名同学去社区进行环保宣传，则选出的同学恰好是一男一女的概率为_________.

【错误分析】问题（1）、问题（2）的错误原因主要是概念不清，不会正确识读条形统计图，不会用样本平均数去估计总体平均数.问题（3）的错误原因主要出在列表的时候没有将男1男2女1女2有效编号，清楚地区分开来，造成重复数，混淆了思维，从而得出错误结论.

【正解分析】（1）144°.（2）640.

（3）列表得出所有等可能的情况数，即可求出所求的概率.

列表如下：

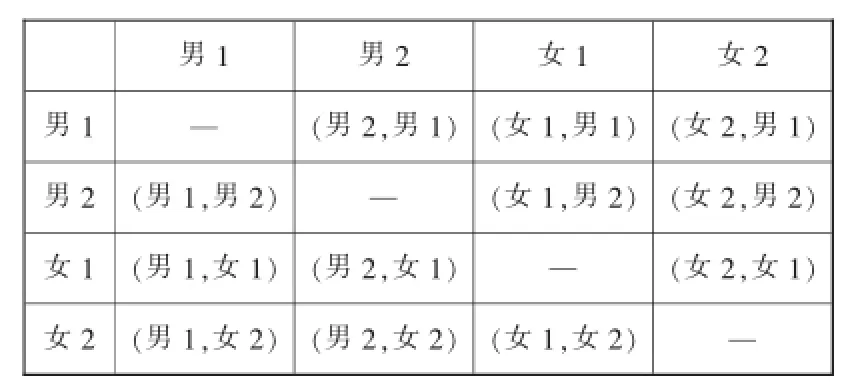
男1　男2　女1　女2 男1　—　（男2，男1）　（女1，男1）　（女2，男1）男2　（男1，男2）　—　（女1，男2）　（女2，男2）女1　（男1，女1）　（男2，女1）　—　（女2，女1）女2　（男1，女2）　（男2，女2）　（女1，女2）　—

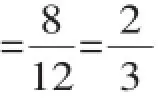
例4（2015·无锡）（1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.（请用“画树状图”或“列表”等方式给出分析过程）

（2）如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是______（请直接写出结果）.

【错误分析】问题中出现人物多，干扰了思维，这个动态的游戏过程较为复杂，初读题时容易出现紧张情绪、手忙脚乱的情况，这时候需要静下心来，仔细审题，画出树状图，进而由特殊到一般去思考问题的规律性，从而得解.

【正解分析】（1）根据画树状图，可得总结果与传到甲手里的情况，根据传到甲手里的情况比总结果，可得答案；

（2）第一步传的结果是n，第二步传的结果是n2，第三步传的结果是n3，传给甲的结果是n（n-1），根据概率的意义，可得答案.

解：（1）画树状图：

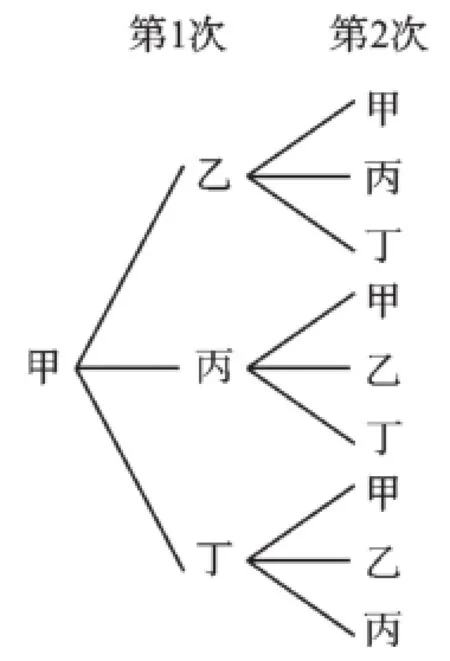
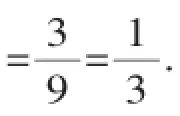
（2）第三步传的结果是n3，传给甲的结果是n（n-1），

（作者单位：江苏省镇江市宜城中学）