“圆心角”度数：弧长计算的关键点

周红娟



“圆心角”度数：弧长计算的关键点

周红娟

弧长计算问题是中考必考知识点，题型不限，公式也很好记，然而解题的难点和关键点常常是待求弧所对的圆心角的度数，因为这些“圆心角”有时不止一个，这是怎么回事呢？请看例题：

例1（2015·苏州）如图1，在△ABC中，AB=AC.分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD.

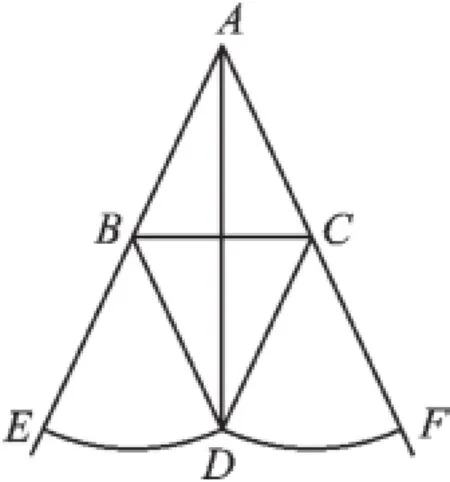
图1

（1）求证：AD平分∠BAC；

（2）若BC=6，∠BAC=50°，求D（E、D（F的长度之和（结果保留π）.

【思路讲解】（1）根据题意得出BD= CD=BC，由SSS证明△ABD≌△ACD，得出∠BAD=∠CAD即可.

（2）由等腰三角形的性质得出∠ABC= ∠ACB=65°，由等边三角形的性质得出∠DBC=∠DCB=60°，再由平角的定义求出∠DBE=∠DCF=55°，然后根据弧长公式求出的长度，即可得出结果.

【规范解答】（1）证明：由作图可知，BD= CD.

∴△ABD≌△ACD（SSS），

∴∠BAD=∠CAD，即AD平分∠BAC.

（2）∵AB=AC，∠BAC=50°，

∴∠ABC=∠ACB=65°.

又∵BD=CD=BC，

∴△BDC是等边三角形，

∴∠DBC=∠DCB=60°，

∴∠DBE=∠DCF=55°.

又∵BC=6，∴BD=CD=6，

【反思回顾】熟练掌握全等三角形和等边三角形的判定与性质，并能进行推理计算是解决该题的关键.从上面的解法步骤来看，求出“∠DBE=∠DCF=55°”是重要进展.

例2（2015·扬州）如图2，已知⊙O的直径AB=12 cm，AC是⊙O的弦，过点C作⊙O的切线交BA的延长线于点P，连接BC.

（1）求证：∠PCA=∠B；

（2）已知∠P=40°，点Q在优弧ABC上，从点A开始逆时针运动到点C停止（点Q与点C不重合），当△ABQ与△ABC的面积相等时，求动点Q所经过的弧长.

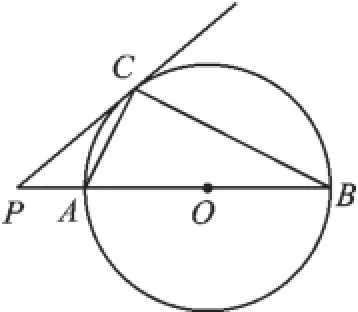
图2

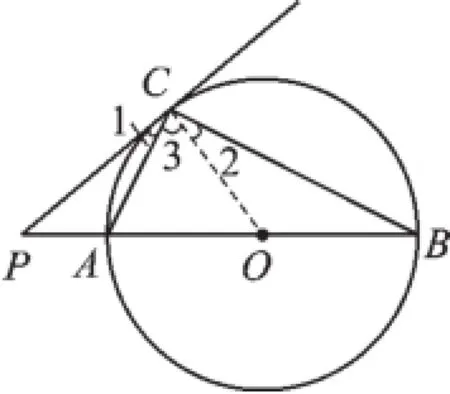
图3

【思路讲解】

（1）如图3，连接OC，由AB是⊙O的直径和PC是⊙O的切线得到∠ACB=∠2+ ∠3=90°和∠PCO=∠1+∠3=90°，从而得到∠1=∠2.再由OC=OB，根据等腰三角形等边对等角的性质得到∠2=∠B，进而得到∠PCA=∠B的结论.

（2）根据同底等高三角形面积相等的性质，分三种情况讨论即可：在⊙O上作点C关于AB的对称点Q，在⊙O上作点C关于点O的对称点Q，在⊙O上作点C关于AB中垂线的对称点Q.

【规范解答】（1）证明：如图3，连接OC，

∵AB是⊙O的直径，

∴∠ACB=∠2+∠3=90°，

∵PC是⊙O的切线，∴OC⊥PC，

∴∠PCO=∠1+∠3=90°，∴∠1=∠2，

∵OC=OB，∴∠2=∠B，

∴∠1=∠B，即∠PCA=∠B.

（2）如图3，∵PC是⊙O的切线，∠P= 40°，∴∠POC=50°.

∵AB=12，∴AO=6.

当△ABQ与△ABC的面积相等时，动点Q在优弧ABC上有三个位置：

①如图4，在⊙O上作点C关于AB的对称点，该点即是满足△ABQ与△ABC的面积相等的点Q，由轴对称性知，∠AOQ=∠POC= 50°，

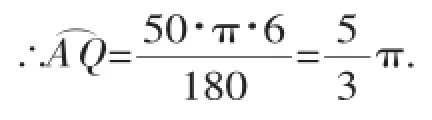
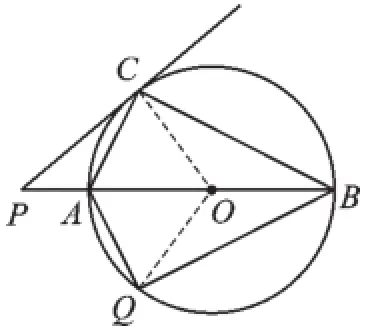
图4

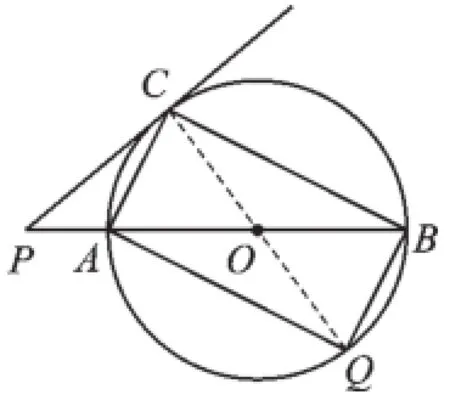
图5

②如图5，在⊙O上作点C关于点O的对称点，该点即是满足△ABQ与△ABC的面积相等的点Q，由中心对称性知，∠BOQ= ∠POC=50°，∴∠AOQ=130°，

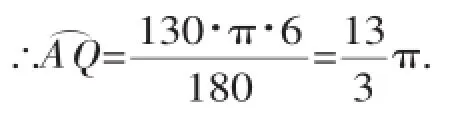
③如图6，在⊙O上作点C关于AB中垂线的对称点，该点即是满足△ABQ与△ABC的面积相等的点Q，由轴对称性知，∠BOQ=∠POC= 50°，∴∠AOQ=230°，

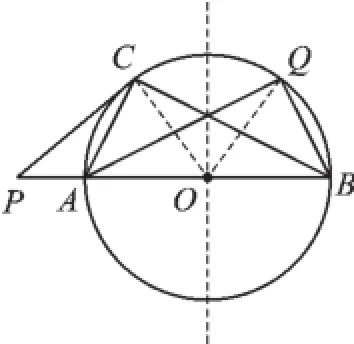
图6

【反思回顾】考题涉及圆周角定理、切线的性质、等腰三角形的性质、同底等高三角形的性质、弧长的计算等多个知识点.第（2）问考查了分类思想，本质上还可以用图7来揭示它们的结构.

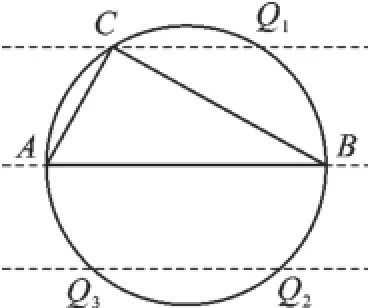
图7

（作者单位：江苏省南通市第一初级中学）