两种方案能“混搭”吗？

○邢台市桥西区北小郭小学　范午英

两种方案能“混搭”吗？

○邢台市桥西区北小郭小学范午英

【问题由来】

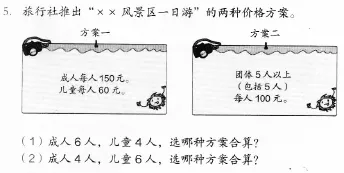
学生审题后，开始计算并比较，如下：

接下来，教师引导学生比较两种情况在方案中的异同。两种情况总人数相同，都是10人。方案二不考虑大人、小孩，只按“人头”算，所以费用相同，都是1000元；方案一中大人费用高，小孩费用低，即大人越多费用越高。“6大4小”和“4大6小”恰好处在1000元上下，造成结论的不同。

教师追问：（1）如果还是10人，但“5大5小”，选哪种方案合算？（2）在总人数不变的情况下，每次把一个大人换成小孩，在方案一中会有什么反应？

课上至此，应该说对教材的利用相当充分。没想到一位学生又举手发言：“我觉得方案一和方案二都不合算。比如“6大4小”，最省钱的办法是6个大人按团体买票，需要100×6=600（元），4个小孩买儿童票，需要60×4=240（元），一共用600+240=840（元）就行。这样买最合算！”很多学生为这一提议“点赞”，“4大6小”的最佳方案也随之出炉：1个小孩加上4个大人买团体票需要500元，另外5个小孩买儿童票，需要300元，一共用800元就行。

面对群情激奋的学生，这位教师却相当冷静。两种方案能不能混搭？题目说得明白：“选哪种方案合算？”即从方案一和方案二中选择一个，现在又冒出个“方案三”，合适吗？

【问题解决】

这是一道实验版教材中保留下来的题目，原为人教实验版四年级下册练习二第10题。对照两版教材，发现有不同之处。实验版教材的方案二规定的是“团体10人以上（包括10人），每人100元”，所以在5～9人时不能买团体票，也就不存在所谓的“方案三”。不知道课标版教材为何要更换数据，难道就是为了引出“混搭”的方案？

当文本上的问题遭遇现实中的挑战，教师该怎么办？是紧盯课本咬文嚼字，纸上谈兵，还是以运用知识技能为本，灵活应对？我愿意选择后者。大家都参加过旅游团，应该有这方面的经验：买门票时，导游会提前统计持有各种减免门票证件的人员，剩下的再买团体票。只要符合购票的要求，风景区就得卖票，谁会限制一个团体必须按同一种方案买票？一般地，方案一针对的是散客，方案二针对的是团体。当总人数达不到团体下限时，只能选择方案一；当总人数达到或超过团体下限时，就有了不同选择。

当然，从审题角度看，重视对问题内涵的把握无可厚非，只是书上的这个问题不妥当，建议把“选哪种方案合算”改为“怎么买票最合算”，就不会有争议了。

基于上述思考，提出以下设计。

师：你的想法很好，突破了刚才的框框，来了个“混搭”！我想那10个人应该很高兴。在总人数不变的情况下，无论几大几小，都是混搭方案最合算吗？

学生饶有兴趣地依次列举，早没了混合计算的枯燥无味。很容易得出结论：只要是10个人，最多花费1000元；如果有儿童则可以花费更少些，最少花费600元（10小）。在“拉小孩凑数”这件事中，因为儿童票比团体票还优惠，所以儿童是“不喜欢”买团体票的，即便买也是凑数，不得已而为之。往往是大人省些钱，小孩多花点钱。如果省得多浪费得少，就合算；反之就不合算了。