考虑消费者广告偏好差异的媒体平台竞争

程贵孙 ，陈宏民，黎 倩

（1.华东师范大学 经济与管理学部，上海 200241；2.上海交通大学 安泰经济与管理学院，上海 200030）

媒体作为一个平台企业，它一边用内容吸引读者或电视观众，一边用广告版面或时段来吸引广告商进行广告投放，广告商投放广告的目的是吸引读者或电视观众来购买广告商的产品。从产业特征来看，媒体是个典型的“双边市场”。双边市场指的是在这个市场中双边用户的交易（交互）活动是通过“平台”进行的，平台向两边用户提供产品或服务，这些产品或服务促使了这两边用户在该平台上达成交易，平台向两边用户制定不同的价格以使它们接入到平台上。双边市场经济现象在很多产业实践中都会发生，如银行卡网络、操作系统、游戏机平台等。在不同产业实践中，双边平台的价格结构和定价策略有着很大的差别，其独特的定价模式已经引起众多经济与管理学者的研究兴趣，纷纷投入到一般性双边市场的定价策略研究领域中［1-3］。

从广告商、消费者两者的交互来看，媒体是个典型的具有双边市场特征的平台企业。媒体向广告商提供广告空间，同时又向消费者提供内容。广告商和消费者之间的交互存在着间接网络效应，即媒体平台拥有的消费者越多，给广告商带来的效用也越大，因为广告商通过在媒体平台上投放广告可以使产品信息广泛传播，媒体平台受众的数量越多，购买商品的概率也越大，因此，媒体受众给广告商带来的是正的间接网络效应。从消费者市场来看，通常媒体平台投放的广告给消费者带来的是“负”的间接网络效应，大多数学者认为消费者是不喜欢广告的，是属于广告厌恶型的，所以媒体平台广告量越多，给消费者带来负效用也越大。因此，越来越多的研究媒体平台的学者基于双边市场框架来分析探讨媒体平台的价格策略和广告量竞争问题。Anderson等［4］把广播电视节目作为公共产品，研究了电视播放公司电视节目供给的市场失灵的问题。研究认为，在电视播放公司垄断或竞争的市场结构下，广告量都有可能高于或低于社会最优的广告量。Barros等［5］采用Shubik-Levitan效用函数研究了媒体平台的双边价格策略，研究表明，在媒体平台垄断市场结构情形下媒体将对广告商不收费，而对消费者收费；在媒体平台竞争的市场结构中媒体将向两边用户都收取费用。Peitz等［6］研究了付费电视和免费电视的广告量竞争问题，研究发现，当消费者不喜欢广告时，免费电视平台播出的广告要多于付费电视平台。Crampes等［7］研究了自由市场进入下媒体平台竞争模型，媒体平台既可以由广告商付费，也可以由消费者付费，研究发现，自由进入下媒体平台竞争导致广告费过高，广告量过少。Kind等［8］考察了媒体平台的数量及其差异化程度是否会提高媒体平台的收入水平，研究发现，如果媒体平台差异性较低时，媒体平台将降低消费者的订阅费，当媒体平台数量越多时，媒体平台获得的广告费也越少。Reisinger［9］考察了在媒体平台对消费者是差异化的，消费者可以根据媒体平台的不同内容选择接入到哪家平台，而媒体对广告商是同质化，即广告商在任何一个媒体平台都可以投放广告，研究在此种情形下媒体平台竞争对价格和广告量的影响，研究发现，在此种情形下，媒体平台可以获得更高的广告费，并且发现媒体平台的利润随着消费者对广告商厌恶程度的增加而提高。

以上对媒体双边市场的研究成果对理解媒体价格竞争与广告量决策，提供了重要的理论方法和研究视角，但不难发现，上述文献存在2个缺陷：

（1）他们都假设消费者是不喜欢广告的，属于广告厌恶型的消费者，广告给消费者带来的是负的效用。然而，在现实生活中，消费者对于广告的偏好并不是完全统一的，有的消费者是喜好广告的，他们喜好拥有更多产品信息的广告。例如在某些汽车、美容等专业类杂志媒体上的广告，汽车或美容消费者却是喜欢看的，他们希望阅读到更多、更详尽的产品信息以便更好地进行产品购买决策，因此，对于专业类杂志上的广告而言，消费者是属于广告喜好型的。Kaiser等［10］对广告喜好型消费者的存在也进行了证实，他们对德国杂志媒体市场进行了实证研究，发现在专业媒体杂志上消费者其实是喜欢阅读有丰富产品信息的广告。

（2）他们所考虑的广告商均为全部覆盖，即广告商都会选择在媒体平台上投放广告。现实中，当广告商发现投放广告的效果不佳时，就不会投放广告，或者广告费太高，广告商也不会投放广告，因此，广告商是部分覆盖的，即只有部分广告商会投放广告，更符合现实。

因此，本文在上述缺陷下考虑消费者广告偏好差异和广告商市场是否完全覆盖，构建新模型研究在不同广告商覆盖下，消费者广告偏好差异对媒体平台价格竞争及其广告量的影响，并对媒体平台竞争下的广告商与社会福利最大化的广告量进行比较，探讨消费者广告偏好差异对媒体平台竞争的效应。本文模型的构建参考并拓展了文献［11-13］中的研究框架。Rasch［11］研究的是双边用户均为“正”网络外部性的双边平台价格竞争，本文考虑的是具有“负”网络外部性媒体平台的价格竞争。文献［12-14］中虽然拓展了消费者的广告偏好差异，但忽视了广告偏好喜好型的消费者对媒体平台竞争的影响，并且所考虑的广告商都是完全覆盖，没有考虑广告商部分覆盖情形。因此，本文创新之处就在于：①放松消费者对广告厌恶的一致性偏好假设，将消费者区分为广告偏好厌恶型和广告偏好喜好型；②放松广告商全部覆盖假设，考虑广告商部分覆盖情形，研究在广告商不同覆盖下消费者广告偏好差异对媒体价格竞争与广告量决策的影响。

1 问题描述与模型建立

1.1 平台利润

为更能刻画消费者广告偏好差异对媒体平台竞争的影响，本文仅考虑由广告费支持的媒体平台，消费者可以免费获得媒体上的内容，如上海地铁报《时代报》、《新民地铁报》都是免费向读者发放，报纸的运营靠广告商的广告费来维持，又如一些商业免费电视也是向观众免费开放，电视运营商靠播放广告商广告维持运营。考虑在一个由广告费支持的媒体市场中存在两家媒体（如免费报纸、商业电视）平台i（i=1，2）。这两家媒体平台分别位于线形城市［0，1］的两端，媒体平台1和媒体平台2分别向广告商制定广告费p1、p2。在给定媒体平台的广告费下，广告商决定是否投放广告，随之两家媒体平台的广告量将确定，分别记为a1、a2（这里的广告量用广告商数量表示）。假设媒体平台内容制作等相关成本为0。因此，媒体平台的利润函数∏i=pi a i。

1.2 消费者效用

消费者总的人数标准化为1，且均匀分布在线形城市［0，1］之间。消费者在同一时间内只能选择1个媒体平台，如同一时间只能阅读1份报纸，观看1个电视节目，即单平台接入。这里将消费者对广告的偏好区分为广告偏好厌恶型和广告偏好喜好型两种类型。广告偏好厌恶型的消费者是不喜欢广告的，广告给消费者将带来负效用，广告量越多，负效用也就越大；而对于广告喜好型消费者而言，广告给消费者带来正的效用，广告量越多，消费者从广告中获得的产品信息就越丰富，获得的效用也就越大。假设广告厌恶型消费者占总消费者人数的比例为λ（0≤λ≤1）。

若两家媒体平台拥有的广告量分别为a1和a2，则坐落于空间x点上的广告偏好厌恶型消费者选择媒体平台1所获得的效用为v-r a1-tx，选择媒体平台2的效用为v-ra2-t（1-x）；坐落于空间y点上的广告偏好喜好型消费者选择媒体平台1所获得的效用为v+r a1-ty，选择媒体平台2获得的效用为v+ra2-t（1-y）。其中，0≤x，y≤1，参数v为消费者的保留效用，并假定保留效用足够大，使得消费者市场被完全覆盖；r为消费者对广告商的网络外部性参数；t为消费者的单位运输成本。根据两类消费者的效用函数，可以找出边际广告厌恶型消费者^x和边际广告喜好型消费者^y，即

1.3 广告商效用

广告商总的数量也标准化为1，且均匀分布在线形城市［0，1］之间，广告商在线形城市中的位置z表示广告商的类型。在给定的广告费p1、p2和媒体平台的消费者规模n1、n2，则坐落于空间z点的广告商选择媒体平台1投放广告所获得的效用为

选择媒体平台2的效用为

其中β是媒体平台的消费者规模给广告商所带来的网络外部性参数，可以理解为看到广告商商品广告后购买其商品的消费者占消费者总数的比例，购买商品的消费者比例越大，给广告商带来的网络效应也越大。

因此，当广告商被完全覆盖时，媒体平台1上的广告量a1=，媒体平台2上的广告量。

然而，当广告商投放广告所获得的效用为负时，某些广告商将不会在媒体平台上投放广告，此时广告商将是部分覆盖的。令为广告商在媒体平台1投放广告与不投放广告的效用无差异点，由

2 博弈均衡分析

媒体平台竞争博弈中参与者的行动次序可分为3个阶段：第1阶段，媒体平台1、2向广告商制定投放广告的广告费，分别为p1和p2以获取最大化利润；第2阶段，广告商在给定广告费之后，决定是否投放广告及在哪个媒体平台投放广告以最大化其效用；第3阶段，不同广告偏好类型的消费者决定接入到哪个媒体平台阅读内容（或观看节目）以最大化其效用。下面根据广告商不同的市场覆盖情况进行博弈均衡分析。

2.1 广告商为完全覆盖

当广告商被完全覆盖时，媒体平台1上的广告量a1=，媒体平台2上的广告量a2=1-。由式（1）和a1=，a2=1-，可得两家媒体平台上投放的广告量分别为：

在博弈的第1阶段，由两家媒体平台的利润函数∏i=p i a i，将式（2）代入利润函数中，可求出该媒体平台竞争的唯一纳什均衡解为

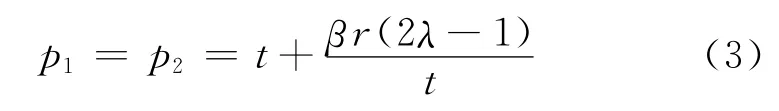
两家媒体平台投放的广告量为a1=a2=0.5，因此，两家媒体平台的利润为

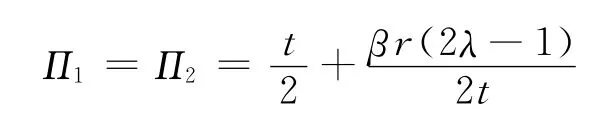
将式（2）代入式（1），可知消费者在两家媒体平台均匀分布，媒体平台有着相同的消费者规模，即n1=n2=0.5。

为保证广告商被完全覆盖，必须使得处于线性城市中点位置（z=0.5）的广告商所获得的利润为非负。将式（3）的均衡价格、媒体平台拥有的均衡的消费者数量n1=n2=0.5及z=0.5代入广告商利润函数中，使得H（z=0.5）≥0，可求得广告商被完全覆盖的约束条件，即

约束条件式（4）说明，只有广告厌恶型消费者的数量比例满足在一定的范围内，广告商才会全部投放广告。若广告厌恶型消费者数量比例超出式（4）的范围，说明消费者市场中存在着过多的广告厌恶型消费者，这就削弱了广告商投放广告的意愿，导致广告商部分覆盖。因为0≤λ≤1，所以必须使得

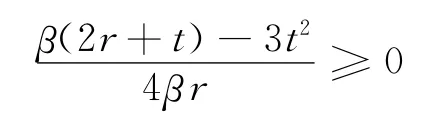
由此得到媒体平台消费者广告规模给广告商带来的网络外部性参数β的约束条件，即

可以很容易地验证

约束条件式（5）则表明，当媒体平台消费者规模给广告商带来的网络外部性参数足够大时，广告商才有动机去投放广告；否则，当消费者规模给广告商带来的网络外部性参数较低时，广告商就不会到媒体平台上投放广告。

考察在广告商是完全覆盖情形下，消费者广告偏好差异对广告费和媒体平台利润的影响，可得结论1。

结论1当广告商为完全覆盖时，随着广告厌恶型消费者比例增大，媒体平台的广告费和利润也将随之增加，即

广告偏好厌恶型消费者人数的增加意味着对广告偏好喜好型消费者人数的减少，媒体为了最大程度更多地吸引消费者，必将减少各自媒体平台的广告投放量，因此，媒体平台只有通过提高广告费来降低广告的投放量。在这个调整广告费的过程中，媒体平台通过提高广告费将达到一个比较均衡的广告投放水平，每个媒体平台将获得一半的广告商市场，从而达到了一个均衡水平，而此时媒体平台获得的利润由于广告费的不断提升而增加。由于广告商完全覆盖，广告费的提高并不会减少广告商对投放广告的需求，只要广告商有投放广告的需求，广告厌恶型消费者比例的增大将进一步削弱媒体平台广告费的价格竞争。

2.2 广告商为部分覆盖

当广告商完全覆盖的条件式（4）不成立时，即当

时，广告商为部分覆盖，此时媒体平台1上的广告量a1=，媒体平台2上的广告量a2=1-。由式（1）和a1=，a2=1-，可得两家媒体平台上投放的广告量分别为：

由媒体平台利润函数中∏i=p i a i，将式（4）代入利润函数中，可求出该媒体平台竞争的唯一纳什均衡解为

两家媒体平台投放的广告量为

两家媒体平台所获得的利润为

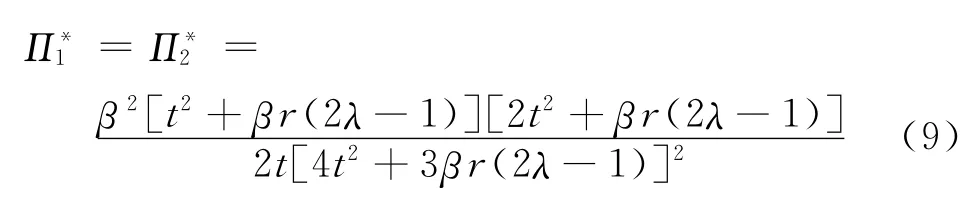
同理，考察在广告商为部分覆盖情形下，消费者广告偏好差异对广告费、广告量和媒体平台利润的影响，可得结论2。

结论2当广告商为部分覆盖时，随着广告厌恶型消费者比例增大，媒体平台的广告费将随之增加，而媒体平台的广告量和利润将随之减少，即

与结论1相同的是，媒体平台的广告费均随着广告厌恶型消费者比例的增长而增加，但与结论1相反的是，在广告商部分覆盖时，媒体平台的利润却是随之减少。这是因为随着广告偏好厌恶型消费者的增多，媒体为了争取更多的消费者不得不降低广告量。所以，尽管广告费是增大了，但广告费的增加不足以弥补广告量的大幅减少而带来的利润损失，因此，总的来说，媒体的利润仍将随着广告偏好厌恶型消费者的增多而减少。

3 社会福利分析

该部分将从社会福利最优的角度来计算媒体平台的最优广告量。由于广告商完全覆盖与现实相差甚远，这里仅考虑当广告商为部分覆盖时的媒体平台社会福利最优的广告量，并进行比较分析。由于广告量等于在媒体平台投放广告的广告商数目，即a1=，a2=1-。利用不同广告偏好类型的消费者所获得的效用函数，可求出总的消费者剩余

接下来，求出两家媒体平台获得的利润和广告商获得的效用，记为

因此，从社会福利角度出发，政府产业管理部门就是要选择合适的广告量水平以最大化社会福利总函数，即WF=CS+∏。将式（10）、（11）代入社会福利总函数中，并对求一阶偏导，可得社会总福利最大化的广告量水平

现在对媒体平台竞争的均衡广告量水平与社会福利最大化的广告量水平作一比较分析。这里并不求出它们的具体差值，而只是从它们的广告量水平关于广告偏好厌恶型消费者占消费者总人数比例λ的函数图像性质上出发作一比较。为分析简便，假设广告商对消费者所产生的网络外部性强度与消费者对广告商产生的网络外部性强度相等，即r=β，即此假设并不妨碍以下结论的合理性。由式（8）、（12）可知，

即它们关于广告厌恶型消费者的比例均是递减函数，并且

这就表明，媒体平台竞争均衡的广告量水平是关于λ的递减凸函数，社会福利最大化的广告量是关于λ的线性递减函数。可用λ（0≤λ≤1）的几个特殊值来求出相应广告量的水平，并对它们的大小关系加以判断。

当λ=0时，

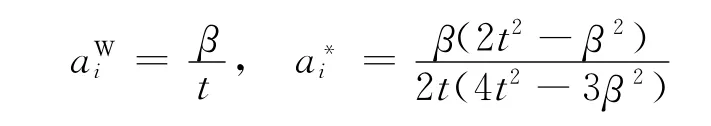
当λ=0.5时，，得到＞；当λ=1时，

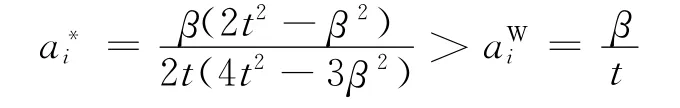
记

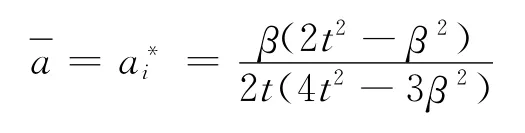
图1（a）～（c）描绘了在不同约束条件下，媒体平台竞争均衡广告量和社会福利最大化广告量的相互关系。图1（a）所示为当t≤β＜时，

的情形。

图1 媒体平台竞争均衡广告量和社会福利最大化广告量的相互关系

由于

且当λ=0.5，以及当λ=1时，由图1可知，必定存在某个，使得。由此可得结论3。

结论3在t≤β＜时，当广告厌恶型消费者占消费者总数的比例较小时（0≤λ＜），媒体平台竞争的均衡广告量小于社会福利最大化的广告量）；当广告厌恶型消费者占消费者总数的比例较大时＜λ≤1），媒体平台竞争的均衡广告量将大于社会福利最大化的广告量。

由结论3可知，当消费者给广告商带来的网络外部性强度较小时（t≤β＜），媒体平台竞争均衡广告量水平与社会福利最大化的广告量水平只存在一个相同点，且在相同点下的广告厌恶型消费者比例较高。媒体平台广告费价格竞争所导致的均衡广告量水平，可能高于也可能低于社会福利最大化的社会广告量水平，这取决于消费者市场中广告厌恶型消费者所占比例的大小。当广告厌恶型消费者所占比例相对较小时，如在0≤λ＜的区域，媒体平台市场竞争的均衡广告量低于社会福利最大化的广告量，此时对于产业规制而言，政府产业管制部门可以放松对广告量投放的管制；相反，当广告厌恶型消费者所占比例相对较大时，如在＜λ≤1的区域，竞争均衡广告量高于社会福利最大化的广告量，此时政府产业管制部门应加强对媒体平台广告量投放管制的力度，减少广告投放量以提高社会总福利。

同理，由

且当λ=0.5，，以及当λ=1时，，由图2可知，必定还存在比例，使得。由此可得结论4。

结论4在β=时，当广告厌恶型消费者占消费者总数的比例λ处在0＜λ＜时，媒体平台竞争的均衡广告量小于社会福利最大化的广告量；当广告厌恶型消费者占消费者总数比例λ处在λ＜λ≤1时，媒体平台竞争的均衡广告量将大于社会福利最大化的广告量。

由结论4和图1（b）可知，当消费者给广告商带来的网络外部性强度时，在广告厌恶型消费者比例为λ=0或时，媒体平台竞争均衡广告量与社会福利最大化的广告量相同。这就说明，在下，当消费者类型都为广告喜好型时（λ=0），与结论3相反，媒体平台竞争均衡广告量等于社会最优广告量。由图1（a）、1（b）的比较来看，除λ=0的点之外，可以得到与结论3相似的结论，即在的区域，此时政府产业管制部门可以放松对广告量播放的管制；在的区域，政府产业管制部门应加强对广告量播放的管制力度。

同理，由于

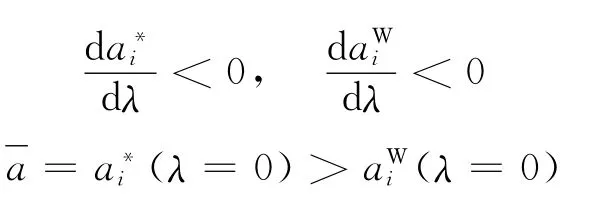
且当λ=0.5，以及当λ=1时，，由图3可知，必定存在

使得

由此可得结论5。

结论5在β＞时，当广告厌恶型消费者占消费者总数比例λ处在时，媒体平台竞争的均衡广告量小于社会福利最大化的广告量；当广告厌恶型消费者占消费者总数比例λ处于，两家媒体平台竞争的均衡广告量将大于社会福利最大化的广告量。

与结论3相反，当消费者给广告商带来的网络外部性强度较大时，即将有更多的消费者购买商品时，广告商越有动机在媒体平台投放广告，而此时既使广告厌恶型消费者所占比例较小，媒体平台竞争所导致的均衡广告量仍然是高于社会福利最大化的广告量。与结论3相同的是，当广告厌恶型消费者所占比例较大时，媒体平台竞争的均衡广告量也是高于社会福利最大化的广告量。而只有在广告厌恶型消费者所占比例处在中间区域时，媒体平台竞争均衡广告量才低于社会福利最大化的广告量。结论5也表明，当广告商在媒体平台投放广告所获得的效用较大时，既使广告厌恶型消费者所占比例较小，而广告喜好型消费者数量更多时，政府产业管制部门也应加强对广告播放量的监管。而当广告厌恶型消费者所占比例处在中间区域时，政府产业管制部门应放松对广告量播放的监管。

4 结论

在社会生活中有很多免费媒体平台如免费报纸、付费商业电视，这些媒体平台通常是向消费者免费，媒体的运营是靠广告费来维持的，因此，免费媒体平台的广告量就成为媒体平台竞争的关键所在，也通常是一些政府行业监管部门关注的对象。

本文在“双边市场”的理论框架下，研究了由广告费支持的媒体平台价格竞争与最优广告量的问题。与以往的研究不同，本文放松了消费者对广告一致性偏好的假设，将消费者对广告的偏好区分为广告厌恶型和广告喜好型，在不同的广告商覆盖情形下，重点考察了消费者广告偏好差异对媒体平台价格竞争与广告量的影响。研究发现，广告厌恶型消费者占消费者总人数比例的增加将使广告费上升；而广告厌恶型消费者对媒体平台利润的影响取决于广告商是否被完全覆盖，在广告商被完全覆盖时，广告厌恶型消费者的增加将使媒体平台利润增加；而在广告商是部分覆盖时，广告厌恶型消费者的增加却使媒体平台利润减少。同时，媒体平台竞争的均衡广告量是过多，还是过少，这取决于消费者给广告商带来的网络外部性的强度和广告厌恶型消费者占消费者人数的比例。

上述研究结论给媒体平台和政府产业管理部门都带来了重要的管理启示：从媒体平台的发展来看，媒体平台运营商应该注重分析广告对消费者的影响，应对消费者市场做好充分的市场调查，分析消费者的广告偏好类型及其比例，并合理引导广告商的广告投放；从广告量产业规制来看，广告量是供应过多，还是供应不足，政府产业管理部分应结合消费者特征和广告商覆盖程度加以区别对待，这取决于消费者给广告商带来的网络外部性的强度和广告厌恶型消费者占消费者人数的比例，对广告量的规制不能搞“一刀切”式的管制方式。

为得到文中的结论，本研究作了简化的假设，如广告商都是单平台投放广告，事实上，广告商有可能在多个不同的媒体平台同时投放广告，即广告商有可能是多平台投放广告。这些都是本文模型可以拓展的领域，相关问题将在后续研究中展开。