基于复合失效模式的寿命分布检验方法*

吴博峰，徐继伟

（1.西安财经学院行知学院，西安　710038；2.西北工业大学自动化学院，西安　710072）

基于复合失效模式的寿命分布检验方法*

吴博峰1，徐继伟2

（1.西安财经学院行知学院，西安710038；2.西北工业大学自动化学院，西安710072）

产品往往受随机失效和耗损失效两种模式的双重影响，因此，构造指数&威布尔分布表征该类产品的失效规律。首先，用图检验法对该类产品的寿命数据进行初步检验；其次，研究了该类产品寿命数据的极大似然估计的求解方法，进一步用伽方检验方法对寿命分布类进行了检验；最后，通过工程仿真例子说明了该方法的具体操作流程，最终验证了方法的正确性。

复合失效模式，图检验法，极大似然估计，拟合优度检测

0　引言

1　指数&威布尔复合分布模型的图检验法

1.1指数&威布尔复合分布模型的构造

由于本文研究产品的寿命可能受随机失效和耗损失效的双重影响，且两者互相独立，构造产品的可靠性分布可表述为下式：

由寿命分布可见当η→0时，产品的可靠性分布无限趋于指数分布，即产品的随机失效完全占据主导地位；而当→0时，产品的可靠性分布无限趋于威布尔分布；其余情况下，产品的寿命即为受随机失效和耗损失效的两方面影响的复合分布。类似地，进一步可构造其余复合分布的模型。由于引言分析显示指数&威布尔分布在工程应用中更具有代表性和普遍性，能表征或拟合大部分的失效规律本文仅以此为代表进行研究，其余情况可类似处理。

1.2基于产品定数截尾寿命试验的分布检验

产品定数截尾寿命试验指从一批产品中随机抽取n台产品投入试验，并统计前r个失效产品的失效时间，得到的试验数据为t1，t2，…，tr，1≤r≤n。通过图检验法对产品的分布类型进行检验。这里，首先构造累计可靠度函数：

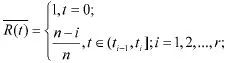
既然已经假定产品的可靠性受两种不同的失效现象独立影响，那么，可将失效数据进行以下对数变换：

6）无论春季嫁接还是夏季嫁接，嫁接时最后一道捆绑的扎带要缠绕固定在接穗芽子的上部，也就是接穗顶部，这个小小的绑扎技巧，避免了因嫁接后解除塑料扎带不及时带来的扎带勒入木质部的隐患。见图1。

在此，若η→0，将累计失效分布函数代入，并将数据填入对数坐标表上，若数据呈现为一条直线，则可认为产品寿命服从指数分布，并通过坐标斜率得到产品的寿命指标，或者根据最小二乘估计得的估计值。

否则，进一步进行对数变换：

将累计可靠度函数带入即可用威布尔图分析法判定产品的寿命是否果真服从威布尔分布，并进一步找到寿命指标的形状参数m和尺度参数η。或用最小二乘估计得到参数的估计值。

当以上两种情况均不能判定产品的寿命分布时，则可判定产品服从指数&威布尔复合分布或可用指数&威布尔分布来近似。

2　指数&威布尔复合分布模型的可靠性估计

由以上分析可知图检验法在大样本情况下能给出粗略的检验和参数估计值，但同时可能存在较大的误差，且在并不服从指数&威布尔分布时还必须用其作近似处理，在某些情况下适用性差。因此，在并不服从指数分布或威布尔分布时，进一步用数理统计方法进行检验分析。首先研究基于寿命试验数据的总体参数极大似然估计。由定数截尾试验数据t1，t2，…，tr，1≤r≤n构造产品的似然函数：

作对数变换

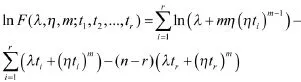
则根据极大似然估计法可列出如下似然方程组：

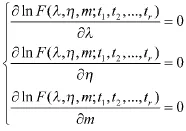
记以上3个似然方程左侧为f1，f2，f3。有如下引理。

引理：上述似然方程存在唯一解

证明：既然认为产品的失效是由随机失效和耗损失效独立造成的，那么假设t1，t2，…，tr中有p个失效时间产生于随机失效，记为t11，t12，…，t1p，而有q个产生于耗损失效，记为t21，t22，…，t2q，其中p+q=r。这里t11，t12，…，t1p，t21，t22，…，t2q只是假定存在但不确切知道的。由文献［1］，根据t11，t12，…，t1p、t21，t22，…，t2q能得到参数，η，m的唯一解，证毕。

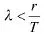
同理，对威布尔分布，其失效率为：

又由威布尔图分析过程知，m＜m'，其中m'为将所有失效数据均拟合为威布尔分布的最小二乘估

3　基于可靠性估计的χ2　拟合优度检验方法检验方法

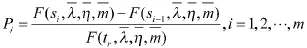
而落在［si，si+1），i=1，2，…，m内的失效个数为r1，r2，…，rm，那么可以用χ2拟合优度检验方法检验总体是否服从指数&威布尔分布。具体过程为：构造统计量

根据R.A.Fisher定理，若总体服从指数&威布尔分布，那么以上统计量服从自由度为m-4的χ2分布，于是可以用χ2检验法检验总体的分布规律。

4　数值仿真算例

电连接器的失效往往受温度、湿度、机械应力等综合因素的影响。因此，电连接器的失效极可能不仅仅是随机失效或耗损失效的单一作用。假设某型电连接器的失效分布函数为

随机抽取120件该型电连接器进行寿命试验，试验到80件电连接器失效为止，通过蒙特卡罗仿真法得到该电连接器的失效数据为

用图估计法检验产品的失效数据并不服从指数分布和威布尔分布，此处略去过程，于是，进一步假设总体服从指数&威布尔分布。按第2节的方法对寿命试验数据进行总体的极大似然估计，估计得（）=（0.001 04，0.000 002 1，1.98）。构造10个区间，根据仿真试验数据构造的区间为［0，50］、［50，100］、［100，150］、［150，200］、［200，250］、［250，300］、［300，350］、［350，400］、［400，450］、［450，500］

上述区间内估计分布的离散概率密度函数

P（10）=［0.065 5 0.119 2 0.083 1 0.107 4 0.102 0 0.096 8 0.091 9 0.127 2 0.082 8 0.138 6］；

而每个区间内的失效数为

N［10］=［5 10 6 5 6 9 8 12 5 14］

检查，于是判定该总体服从指数&威布尔分布。这个仿真算例同时验证了本文所提出方法的正确性和可操作性。

5　结论

针对产品受多种失效模式共同影响的情形，本文构造了指数&威布尔寿命分布模型。并研究了寿命数据的一般分布可靠性检验方法。首先，用图分析法对寿命数据进行指数分布检验和威布尔分布检验，这两种检验方法均无法作出判定时，进一步构建了基于极大似然估计的的分布类型拟合优度检验方法，并进一步对可靠性分析做出评价。本文最后通过工程仿真案例说明了该方法的可用性和有效性。该方法适用于复杂失效模式产品的可靠性试验数据快速评价过程。

［1］JOHN S.Weibull component reliability-preduction in the presence of masked data［J］.IEEE Transactions on Reliability，1996，45：229-232.

［2］张萌，陆山，杨扬.截尾情形下基于屏蔽数据的部件可靠性分析［J］.系统工程学报，2012，27（1）：137-144.

［3］盛骤.基于隐蔽的系统成败型数据的元件可靠性的极大似然估计和区间估计［J］.工程数学学报，1999，16（4）：107-109.

［4］张铁岩，王承民，孙秋野，等.一类基于改进Weibull分布模型电力电缆寿命评估方法［J］.中国工程科学，2008，10 （10）：42-46.

［5］曹晋华，程侃著.可靠性数学引论［M］.北京：高等教育出版社，2006.

［6］茆诗松.高等数理统计［M］.第2版.北京：高等教育出版社，2006.

Life Distribution Hypothesis Testing Method Based on Complex Failure Mode

WU Bo-feng1，XU Ji-wei2
（1.School of XING ZHI，Xi'an University of Finance and Economics，Xi'an 710038，China；2.School of Automation，Northwest Polytechnical University，Xi'an 710072，China）

Product life is often affected by both random failure mode and degradation failure mode，thus this paper constructs the Exponential&Weibull failure distribution to reflect this failure mode.Firstly，a figure test method is used to preliminary inspect of the life data of the products；secondly，this paper researches the lifetime datas of the product by maximum likelihood estimation method，thirdly，gamma-square test is used to determinate the for life distributions of the product；Finally，simulation example is applied to show the concrete operational procedures of this method，and verificate of the correctness of this method.

complex failure modes，fig testing method，MLE，gamma-square test

TB114.3

A

1002-0640（2016）07-0168-03

2015-06-15

2015-07-12
*

国家青年科学基金（61201321）；福建省教育厅A类科技基金资助项目（JA12375）

吴博峰（1983-），男，福建安溪人，硕士，讲师。研究方向：可靠性理论与应用、应用概率统计。