弹簧质点系统的一类振动反问题

万文婷

(荆楚理工学院 数理学院，湖北 荆门 448000)



弹簧质点系统的一类振动反问题

万文婷*

(荆楚理工学院 数理学院，湖北 荆门 448000)

本文讨论了系统惯性能量约束下的接地弹簧质点系统的构造问题。通过求解一类广义逆特征值问题，得到问题有解的一个充分必要条件，并给出解的计算表达式、数值算法及算例。

接地弹簧质点系统；广义逆特征值问题；Jacobi矩阵；特征对

工程实际中常遇到例如桩的纵向振动问题，这类问题中杆是沿长方向与弹性基础相连的，其杆的纵向振动反问题利用集中质量法或有限差分法可离散为弹簧质点系统的振动反问题。弹簧质点系统的振动反问题是动力学反问题中的基本问题，相关研究在振动控制、结构设计、参数识别等方面都有着重要的应用。所谓弹簧质点系统的振动反问题，就是由已测量的部分频率(特征值)和相应的振型(特征向量)确定系统其余物理参数。此类问题在数学上常转化为Jacobi矩阵的特征值反问题，目前，关于Jacobi矩阵特征值反问题的研究已有一些较好的结果[1-5]。文[6-11]分别研究了由两组特征值、由一个或两个特征对、由两个不完整特征对确定弹簧质点系统的振动反问题，并给出了相应问题的可解性条件及求解的数值方法。结合工程实际问题，本文考虑由系统的部分物理参数、两个特征对及系统的惯性能量构造了一类不同于文[11]的弹簧质点系统，得到了相关问题解的存在条件、表达式及算法。

前p个质点通过弹簧接地的n自由度弹簧质点系统(图1)对应的广义特征值方程为

KX=λMX，其中λ和X分别称为矩阵对(K，M)的特征值和特征向量，λ=ω2，ω是固有频率，X为振型，M=diag(m1，m2，…，mn)是质量矩阵，质点质量mi>0，未接地弹簧刚度ki>0(i=1，2，…，n-1)，接地弹簧刚度cj>0(j=1，2，…，p)，

为刚度矩阵。

图1　接地弹簧质点系统

本文考虑如下弹簧质点系统的能量约束问题：

KX=λMX，KY=μMY，

(1)

记ui=xi-xi-1，vi=yi-yi-1，li=λxivi-μyiui，i=1，2，…，n，

hi=λxivi+1-μyiui+1，i=1，2，…，n-1，

zi=(λ-μ)xiyi，fi=xivi+1-yiui+1，gi=xivi-yiui，ri=kifi-ki-1gi，

si=kihi-ki-1li，i=1，2，…，p，

这里，x0=y0=0， k0=0。

1　问题唯一解的条件

若mi>0(i=1，2，…，n)，则方程KX=λMX等价于方程JX=λX，这里J=M-1K是n阶Jacobi矩阵。

定义[12]对n维实向量X=(x1，x2，…，xn)T，其分量组成的序列的符号改变数(值为零的项略去不计)记为S(X)。

由于Jacobi矩阵的特征值为互不相等的实数，不妨设n阶Jacobi矩阵J的特征值为λi>0(i=1，2，…，n)，按升序排列为λ1<λ2<…<λn，则有

引理[12]设(λ，X)是n阶Jacobi矩阵J的特征对，则(λ，X)是J的第i个特征对的充分必要条件是S(X)=i-1， i=1，2，…，n。

式(1)可改写成

(2)

i=1，2，…，n，这里，k0=kn=0， x0=y0=0， cp+1=…=cn=0。

定理问题有唯一解的充分必要条件是

(1)zi≠0，且zi，ri，si同号，i=1，2，…，p-1；

hi≠0，且hi，li，qi同号， i=p+1，p+2，…，n-1；

xnun>0， ynvn>0， ln=0；

(2) t≠0，且w与t同号；

(3) zp≠0，且zp，rp，sp同号；

(4) S(X)=i′-1，S(Y)=j′-1。

证明当i=1，2，…，p-1时，

即zi≠0，i=1，2，…，p-1，且

(3)

又mi>0，ci>0，因而，zi，ri，si同号，i=1，2，…，p-1。

当i=p时，不妨设kp已知，则

(4)

又mp>0，cp>0，则zp，rp，sp同号。另外，mp与cp还可展开为

当i=p+1，p+2，…，n-1时，不妨设kp已知，则

(5)

又ki>0，mi>0，因而hi，li，qi同号，i=p+1，p+2，…，n-1。同样，ki与mi也可展开为

当i=n时，不妨设kp已知，则

(6)

(7)

因为kp>0， 所以t≠0，且w与t同号。再结合引理，即得定理。

2　算法和算例

算法1) 计算S(X)，S(Y)。 若S(X)≠i′-1 或S(Y)≠j′-1，则转6)；

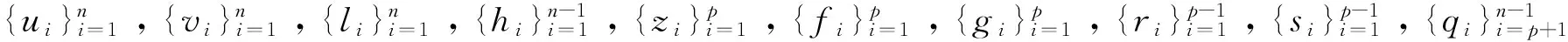
3) 若某个zi=0或zi，ri，si(i=1，2，…，p-1)不同号，则转6)；

若某个hi=0或hi，li，qi(i=p+1，p+2，…，n-1)不同号，则转6)；

若xnun≤0或ynvn≤0或ln≠0，则转6)；

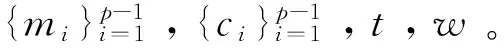
5) 计算kp，rp，sp。若zp=0或zp，rp，sp不同号，则转6)；

6) 解无法唯一确定，退出程序；

现需构造出K和M，设计出一个9自由度的接地弹簧质点系统，且要求(λ，X)和(μ，Y)分别为系统的第3个和第8个特征对。

由算法，得S(X)=2，S(Y)=7。

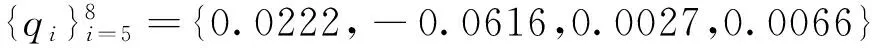
因而，t=2.4979，w=5.2239。由式(7)，得k4=2.0913，因而，r4=0.1379，s4=0.2097。

用Matlab重新计算KX=λMX的广义特征值全体为

σ(K，M)={0.0287，0.3413，0.8411，1.4231，1.7295，2.1545，2.6482，3.3918，4.4495}。

特征值λ=0.8411对应的特征向量为

X=(0.0232，0.0502，0.0931，0.1758，0.3745，0.1919，-0.4855，-0.4159，0.6096)T，

特征值μ=3.3918对应的特征向量为

Y=(-0.9155，0.3587，-0.0829，-0.1469，0.0670，-0.0177，0.0052，-0.0011，0.0002)T。

3　结束语

本文研究了系统惯性能量约束要求下，由接地弹簧质点系统的部分物理参数和两个模态构造真实振动系统的设计问题。将问题归结为一类Jacobi矩阵的逆特征值问题，给出了问题的可解性条件，并提供了问题求解的数值算法和计算实例。

[1]WuXQ，JiangEX.AnewalgorithmontheinverseeigenvalueproblemfordoubledimensionalJacobimatrices[J].LinearAlgebraAppl， 2012， 437(7): 1760-1770.

[2]WuXQ.AdivideandconqueralgorithmonthedoubledimensionalinverseeigenvalueproblemforJacobimatrices[J].ApplMathComput， 2012， 219(8): 3840-3846.

[3]GS.Guseinov.OnaninverseproblemfortwospectraoffiniteJacobimatrices[J].ApplMathComput， 2012， 218(14): 7573-7589.

[4]WeiY.AJacobimatrixinverseeigenvalueproblemwithmixeddata[J].LinearAlgebraAppl， 2013， 439(10):2774-2783.

[5]WeiY.InverseeigenvalueproblemofJacobimatrixwithmixeddata[J].LinearAlgebraAppl， 2015， 466: 102-116.

[6]GML.Gladwell，JA.Gbadeyan.Ontheinverseproblemofthevibratingstringorrod[J].QJMechApplMath， 1985， 38: 169-174.

[7]PNylen，FUhlig.Inverseeigenvalueproblemsassociatedwithspring-masssystems[J].LinearAlgebraAppl， 1997， 254: 409-425.

[8]HuangXT，HuXY，ZhangL.Physicalparametersreconstructionofafixed-fixedmass-springsystemfromitscharacteristicdata[J].JComputApplMath， 2007， 206(2): 645-655.

[9]YMRam，GML.Gladwell.Constructingafiniteelementmodelofavibratingrodfromeigendata[J].JSoundVib， 1994，169(2):229-237.

[10]BaiZJ.Constructingthephysicalparametersofadampedvibratingsystemfromeigendata[J].LinearAlgebraAppl， 2008， 428: 625-656.

[11]TianX，DaiH.Inversemodeproblemsforthefiniteelementmodelofavibratingrod[J].ApplMathComput， 2009， 214(2): 479-486.

[12]GML.Gladwell.InverseProblemsinVibration[M].Dordrecht:KluwerAcademicPublishers， 2004.

(责任编辑：曾晶)

A Vibration Inverse Problem of Spring-Mass System

WAN Wenting*

(School of Mathematics and Physics， Jingchu University of Technology， Jingmen 448000， China)

A construction problem for grounding spring-mass system under the inertial energy restriction was discussed. By solving a class of general inverse eigenvalue problems， a necessary and sufficient conditions for solution of the problem was obtained. And computational expressions of the solution， numerical algorithms and numerical example were given.

grounding spring-mass system; general inverse eigenvalue problem; Jacobi matrix; eigenpair

A

1000-5269(2016)03-0004-04

10.15958/j.cnki.gdxbzrb.2016.03.02

2016-03-28

湖北省教育厅科研项目(B2016264)；荆楚理工学院校级科研基金项目(QN201607)

万文婷(1982-)，女，讲师，硕士，研究方向：数值代数，Email: wentingwan@163.com.

万文婷，Email：wentingwan@163.com.

O151.21