一类脉冲捕食微分系统周期解的局部稳定性分析

唐晓伟

(1.齐鲁师范学院 数学学院，山东 济南 250200；2.山东师范大学 数学科学学院，山东 济南 250014)



一类脉冲捕食微分系统周期解的局部稳定性分析

唐晓伟1 ,2*

(1.齐鲁师范学院 数学学院，山东 济南 250200；2.山东师范大学 数学科学学院，山东 济南 250014)

本文通过建立转换集并引入映射结构研究了一类脉冲捕食微分系统周期解的局部稳定性，给出了其周期解局部稳定性分析的充分条件，克服了因脉冲影响而带来的系统不连续的困难。

周期解；稳定性；脉冲

在对生物种群的管理和利用中，维持种群的生态平衡至关重要。通常人们会采取一些措施以保证种群维持最佳的状态，例如通过收获或投放一定数量的目标物种等。人们对种群管理和利用的目的与程度不同会导致对种群的干预手段也不同，这些干预手段可以是连续性的也可以是间断性的。间断性的干预手段相对于种群的整个生存过程是短暂的，瞬时的，但是对种群的影响是不容忽视的。因此，用连续种群动力系统来描述种群的动力学行为是不够的，在连续种群动力系统的基础上，通过增加符合实际的脉冲条件建立脉冲种群动力系统[1-3]，用脉冲种群动力系统来研究种群动力学行为的复杂性和多样性更符合现实情况的需要。

脉冲捕食微分系统是一类常见的脉冲种群动力系统[2-3]，很多学者致力于其周期解的稳定性研究[3-8]。文献[8]利用常微分方程的定性理论和几何方法给出了具有状态脉冲的脉冲种群微分系统周期解存在性的结果。文献[9]在研究不连续动力系统的复杂动力学行为时，提出了一种基于转换平面和映射结构的方法，这种方法在研究周期解的稳定性时只需根据周期解所满足的微分系统，建立映射结构，通过映射结构所决定的广义特征值就能确定周期解的局部稳定性和分支情况，克服了脉冲影响造成的系统在脉冲点处不连续的困难。在此基础上，本文利用映射结构研究一类具有状态脉冲的两种群捕食微分系统周期解的局部稳定性和分支情况，给出了系统周期解局部稳定性和分支情况判断的充分条件。

1　预备知识和基本结果

考虑如下的两种群捕食微分系统：

(1)

式(1)可以用来描述捕食者与被捕食者之间的相互作用,其中x(t)表示被捕食者的种群密度,y(t)表示捕食者的种群密度,a>0为被捕食者的增长率,d>0为捕食者的死亡率,r≥0为种群竞争系数,b>0为捕食者的捕食率,c>0为被捕食者转化为捕食者的转化率。

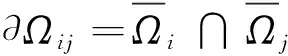
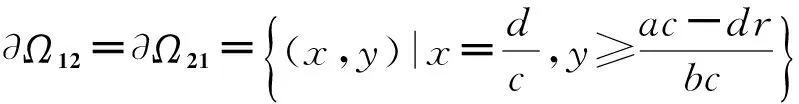
(2)

由于相邻区域Ωi,Ωj的边界均为直线,故由Albert C.J.Luo[9]的流转换理论,给出如下定理。

定理1若系统(1)满足(H1),则系统(1)的从Ω1出发的轨线必将都进入Ω2,从Ω2出发的轨线必将都进入Ω3,从Ω3出发的轨线必将都进入Ω4,从Ω4出发的轨线必将都进入Ω1。

证明相邻区域Ωi,Ωj的边界∂Ωij的法向量分别为

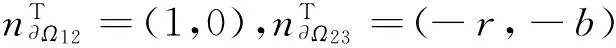
设系统(1)从Ω1出发的轨线在时刻tm到达边界∂Ω12,此时

nΤ∂Ω12·F(1)(X(tm-))

=x(tm-)·(a-rx(tm-)-by(tm-))<0。

同时,nΤ∂Ω12·F(2)(X(tm+))<0,其中tm-表示此时轨线位于Ω1内,tm+表示此时轨线位于Ω2内,故从Ω1出发的轨线若到达边界∂Ω12,则必进入区域Ω2。

另一方面,我们证明从Ω1出发的轨线若能在时刻tn到达边界∂Ω14,则其必不能穿过∂Ω14。此时

=(-r)·[x(tn-)·(a-rx(tn-)-by(tn-))]-

by(tn-)·[cx(tn-)-d]<0,

同样的,可以证明从Ω2出发的轨线必将都进入Ω3,从Ω3出发的轨线必将进入Ω4,从Ω4出发的轨线必将都进入Ω1。

2　主要结果及其证明

当被捕食者的密度x到达被捕食者种群最大容量ET时,可以采取人工捕捉被捕食者或投放捕食者的控制措施,以达到保持生态平衡的目的。于是,考虑如下的具有状态脉冲的脉冲捕食微分系统:

(3)

其中00。

定理2[10]若系统(3)有周期解,且满足(H1)和如下的(H2), (H3),其中

则系统(3)的周期解是唯一的。

定理3若系统(3)满足假设(H1),那么其周期解的局部稳定性分析可由广义特征值理论得到。

Σ={(x,y)|x=ET,y>0}。

于是映射Pi的控制方程为:

(4)

(5)

满足P(ET,y)=(ET,y),(ET,y)是转换集Σ中的一点,i=1,2,…，k。对于扰动ΔZi=Δ(xi,yi)Τ,周期解Z(t)稳定性分析的变分方程为ΔZi+NT=DP·ΔZi,其中T表示Z(t)的周期,N为正整数,

由(4)和(5),可作出复合映射DP的广义特征方程为det(DP-λE)=0,其中E为单位矩阵,求出周期运动Z(t)的广义特征值λ1,λ2,由λ1,λ2的符号及模的大小可得如下结论:

(i) 若λ1,λ2的模均小于1,则系统(3)的周期解Z(t)是稳定的;

(ii) 若λ1,λ2中至少有一个模大于1,则系统(3)的周期解Z(t)是不稳定的;

(iii) 若λ1,λ2中一个为1,而另一个在单位圆内,则系统(3)的周期解Z(t)存在鞍结分支;

(iv) 若λ1,λ2其中一个为-1,而另一个在单位圆内,则系统(3)的周期解Z(t)存在倍周期分支;

(v) 若λ1,λ2为一对共轭复根,且模为1,则系统(3)的周期解Z(t)存在Neimark分支；

(vi) 若λ1,λ2中至少一个为0,此时为退化情形。

证毕。

[1] 陈兰荪,宋新宇,陆征一.数学生态模型与研究方法[M].成都:四川科技出版社,2003.

[2] 郭红建,李景杰,宋新宇.一类具有常数脉冲投放的三种群捕食系统[J].数学的实践与认识,2006,36(18):223-228.

[3] HUANG Mingzhan ,SONG Xinyu ,GUO Hongjian, et al.Study on species cooperative systems with impulsive state feedback control[J]. Journal of Systems Science and Mathematical Sciences,2012,32(3):265-276.

[4] ZHANG Yujuan, LIU Bing, CHEN Lansun.Extinction and permanence of a two-prey one-predator system with impulsive effect[J]. IMA journal of Mathematical Medicine and Biology, 2003,20 (4):309-325.

[5] Kuang Y. Differential equations with applications in population dynamics[M].San Diego: Academic PressINC,1993.

[6] Abdelkader L,Arino O. Bifurcation of non trival periodic solutions of impulsive differential equations arising chemotherapeutic treatment[J].Dynamical Continuous discrete impulsive system,2000,7(2):265-287.

[7] Jiang G R.Complex dynamics of a Holling ype II prey-predator system with state feedback control[J].Chaos,solutions and fractals,2007,31(2):448-461.

[8] PEI Yongzhen , ZENG Guangzhao, CHEN Lansun.Species extinction and permanence in a prey-predator model with two-type functional responses and impulsive biological control [J].Discrete and continuous dynamics system,2008,52(1):71-81.

[9] Albert C J Luo. Discrete and switching dynamical system [M]. Beijing:Higher education press, 2012.

[10]宋新宇,郭红建,师向云.脉冲微分方程理论及其应用[M].北京:科学出版社,2011:225-226.

(责任编辑：周晓南)

Local Stability Analysis of the Periodic Solutions for an Impulsive Predator-Prey Differential Systems

TANG Xiaowei1, 2

(1.Mathematical School, Qilu Normal University, Jinan 250200, China;2. School of Mathematical Science, Shandong Normal University, Jinan 250014, China)

The local stability of periodic solution for a class of impulsive predator- prey differential systems was studied by setting up transition sets and mapping structures. Sufficient conditions for the local stability analysis of the periodic solutions were given, which overcome the difficulty of the discontinuity caused by impulsive effects.

periodic solutions; stability; impulse

A

1000-5269(2016)03-0001-03

10.15958/j.cnki.gdxbzrb.2016.03.01

2015-10-20

国家自然科学基金项目资助(11571082)；齐鲁师范学院校级青年教师项目资助(2014L1002)

唐晓伟(1983-)，女，讲师，硕士，研究方向：微分方程稳定性，Email：dangmy@163.com.

唐晓伟，Email：dangmy@163.com.

O175.14