完全学分制下应用型高校大学数学答疑模块探索和实践

上海第二工业大学文理学部　罗　琳　刘丽丽　谢晓强



完全学分制下应用型高校大学数学答疑模块探索和实践

上海第二工业大学文理学部罗琳刘丽丽谢晓强

数学在大学教育体系中占有重要地位，是理工类和经管类学生学习其他课程的重要基础课程，是培养具有数学素养的工程技术人才和管理人才的必备课程。多年来，各高等院校特别重视对大学数学的教学改革与创新，大学数学的教学工作不断被提出新的要求，特别是在完全学分制下，如何提高大学数学的教学质量和学生学习质量，如何培养具有创新思维能力的应用型人才一直受到全社会关注。本文主要研究在完全学分制下大学数学的答疑模块，通过对大学数学授课式答疑模块、在线式答疑模块、跟踪式答疑模块和讨论式答疑模块等探索与实践，提出大学数学公共课程教学改革的具体措施，希望能为大学数学教学改革提供有益参考和借鉴。

大学数学 答疑模块 教学改革

大学数学是高校理工类和经管类学生必须学习的基础理论课程，如《微积分》《线性代数》《概率论与数理统计》等课程。这几门课程使学生可以系统地掌握大学数学的基本知识，必要的理论基础和常用的计算思维方法，其目的是为了培养学生的计算能力、逻辑思维能力和分析归纳总结能力，使学生能在后续的专业课程中利用大学数学的有关知识解决实际问题。本文提出开展大学数学辅导答疑模块的探讨和实践，希望能为大学数学教学改革提供有益参考和借鉴，为创新型应用人才培养提供有益帮助。

一、授课式辅导答疑

大学数学课程知识具有抽象性和逻辑性强，各知识点之间具有连贯性，应用定理性质解决问题的灵活性较强，定理性质多，学生在课堂学习过程中能做到当时懂，但课后产生课堂知识遗忘、前后知识混淆甚至面对课后习题无从下手的尴尬。

课堂教学结束之后，由大学数学教研室统一安排一次或者两次公共习题课，提供授课式辅导答疑，由有经验的大学数学教师担任集体授课辅导工作。

授课辅导答疑过程中，教师可以先把新知识与旧知识做串讲提炼，归纳主要知识点以及知识点之间的联系，然后通过典型习题讲解的方式归纳常见解题思路和解题突破口，启发式地逐步传授给学生，帮助学生通过习题辅导反思解题突破口，达到触类旁通、举一反三的效果。

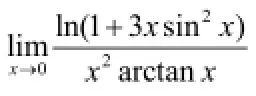
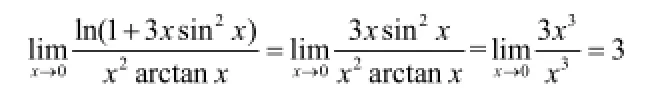
函数无穷小替换的思想可以使问题简单化，这种方法在求函数极限过程中非常重要。教师在课堂教学中应将该方法传授给学生，但学生运用该方法过程中还会遇到用错或无法灵活处理的问题。集体授课式辅导过程中，教师可以将该方法通过典型例题的方式再次传授给学生，强化学生记忆。

二、在线式辅导答疑

各高校逐步推行在线学习平台，为学生创造自由、开放式的补充学习机会，学生可以针对课堂上不清楚的知识点通过上网在线学习的方式补充学习、补充练习、在线测试，加强对每个重要知识点的掌握程度。

我校采取在线式答疑模块，学生通过课堂授课学习、课后在线补充学习练习后在规定的时间内自行进行一次小测试。测试试卷随机出现，相邻两个学生的试卷各不相同，但考察的知识点一致。通过测试，学生可以及时判断自己对这部分知识的掌握的情况。

为了方便学生在线学习，教师可以每周确定两个晚自习的时间开展在线答疑。这样的答疑模块不能满足学生的所有学习要求，但可以帮助学生解决在学习大学数学过程中遇到的问题，尤其是共性问题。只要学生在线，有一个学生提出，教师答疑后其他同学都可以共享这份资源。这个过程可以补充课堂教学不足，对提高班级整体教学质量具有帮助作用。

2014-2015学年度第一学期，我校按照这一过程开展大学数学在线辅导答疑，学生的期末考试及格率得到明显提高。例如，《微积分A》及格率达到了80%以上，其中90分以上20%。具体情况如下：

1.全校平行班共有1133个同学参加考试，期末考试成绩分布如下：

分数段90-100 80-89 70-79 60-69 0-59学生人数234 240 217 172 270百分比20.60％ 21.10％ 19.10％ 20.30％ 15.10％

从上表可以清楚地看出每个成绩段的学生人数在20％ 左右，60 分以下的学生比例缩小。

2. 提高班考试情况：提高班共108 人，成绩分布如下：

分数段90-100 80-89 70-79 60-69 0-59学生人数53 22 16 8 9百分比49.07％ 20.30％ 14.80％ 7.40％ 8.30％

从上表中可以看出，提高班有50％ 左右的成绩分布在90～100分，即提高班高分比例高而不及格率控制在10%以下。

三、跟踪式辅导答疑

大学数学可以培养学生的数学思维能力，更重要的是培养学生解决实际问题的应用能力。而工科和商科学生进校一至两年的时间里基本能完成大学数学三门基础课程的学习，学生在这个基础上能否将之转化为数学应用能力还需要跟踪式答疑辅导过程。这就是说，大学数学课程的学习不仅是大一大二的学生，还要贯穿到大学四年中，大三、大四期间大学数学学习过程主要体现在竞赛辅导方面，如数学建模、数学竞赛等。这部分答疑工作可以通过竞赛辅导、竞赛培训方式进行。

例如，数学建模竞赛答疑辅导过程中，我们可以给出部分历年全国大学生数学建模问题，这些问题都是一些实际应用问题，但本质来说是数学问题。学生需要根据实际问题建立合理的数学模型（如数学方程或方程组），再用大学数学课程中的数学知识求解建立的模型。这个过程中，学生需要教师辅导答疑，逐步解决问题。

又如，2010年全国大学生数学建模竞赛A题：储油罐的变位识别问题需要建立数学模型研究罐体变位后对罐容表的影响。这个问题需要用到大学数学中的重积分知识、泰勒公式用于近似计算等知识。通过教师的跟踪式辅导，学生充分体会到大学数学知识是怎样被应用到实际问题解决过程中的，逐步提升大学数学知识的实际应用能力。

大学数学辅导答疑贯穿大学四年学习过程，能坚持参加答疑辅导的学生都是数学能力提升最快的学生，是最具创新思维能力的学生。跟踪式辅导答疑需要培养学生的学习兴趣，兴趣是持续跟踪答疑的基础，是数学能力不断提升的过程，是解决问题的能力突飞猛进的过程。这个过程对高等教育创新型应用人才的培养具有重要意义。

四、讨论式辅导答疑

完成授课式答疑模块后，部分有数学思维能力的学生希望有机会挑战自己，主动要求解决一些比课本难度大的问题，拿出其他资料上的问题向教师请教和讨论。针对这一现象，一个知识内容或一个重要知识点结束后，教师可以穿插一些有挑战性的数学问题供学生分组讨论（group study），充分发挥学生个体和集体的智慧甚至是多种解决问题的方法，发挥学生主体的积极思考问题、解决问题的能力，开拓教师的教学方法，开阔学生的创新思维能力，帮助学生提高应用大学数学知识的能力。辅导答疑模块中，教师可以讨论数学题的解法，也可以讨论实际应用问题。

例如，由于竞赛题具有发散思维特点，比课本里的题目难，教师可以组织参赛学生一起讨论，研究解决问题的着眼点、出发点和解决问题所需的知识点、突破口等。学生可以综合自己掌握的大学数学知识提出解决问题的方法。这一过程不仅能一题多解，更重要的是锻炼了学生的思维能力，拓宽了学生的知识面，更重要的是提高了学生持续学习数学知识、解决数学问题的兴趣。

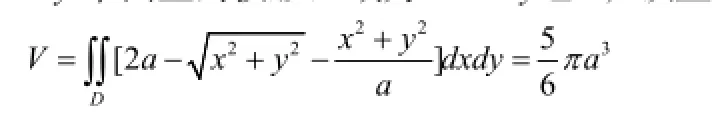
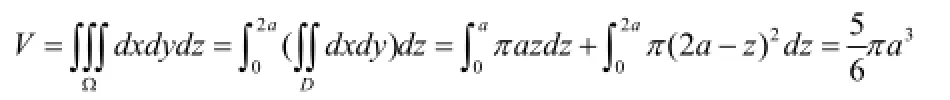
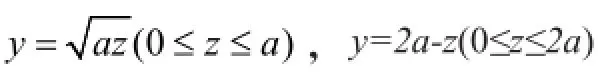
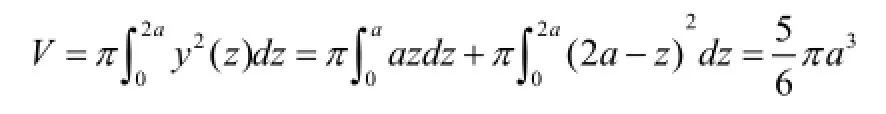
这类几何应用问题可以提高学生运用大学数学知识解决实际问题的能力。通过分析讨论，学生运用不同的大学数学方法找到解决同一问题的不同突破口，获得解决这一问题的最优方法，拓宽知识面，培养运用数学知识解决应用问题的思维和兴趣，提高应用大学数学知识的能力。

五、结束语

大学数学教学旨在培养学生的综合创新思维能力、综合实践应用能力。对于应用型科技大学来说，在完全学分制下学生学习大学数学知识不仅体现在课堂教学中，更要充分利用辅导答疑模块提高应用数学知识解决实际问题的能力。而这些能力的培养不仅体现在大一、大二学生的数学课堂教学中，而要贯穿大学四年的学习，使学生对这种思维能力和实践能力的培养形成一种兴趣、一种习惯、一种常态。本文提到的授课式辅导答疑、在线式辅导答疑、跟踪式辅导答疑、讨论式辅导答疑等四大模块只是众多答疑模块的一部分，希望能为大学数学教学改革提供有益参考和借鉴，希望能为高校创新型人才培养提供有益帮助。

［1］朱志斌.高校辅导答疑的探讨［J］.高教论坛，2007

［2］席 敏，肖爱玲.浅谈大学数学公共学习中心的构建［J］.广东技术师范学院学报（自然科学版），2015

［3］陈 丽.大学数学学习困难因素分析及对策［J］.学园，2014

（本文受基金资助：上海第二工业大学教学改革项目，编号：A01GY15H018；应用数学学科，编号：XXKPY1604）

ISSN2095-6711/Z01-2016-06-0185

罗琳（1968.02—），女，上海第二工业大学，教授，博士研究生