数形结合方法在高中数学教学中的具体应用探讨
2016-08-16山东
◇ 山东 刘 娅
数形结合方法在高中数学教学中的具体应用探讨
◇ 山东 刘 娅
数形结合的方法能够增强学生对数学知识的理解,通过数形结合法可挖掘数学问题的中心思想,对于提高学生逻辑思维能力起到积极的作用.在高中数学教学中,教师可运用数形结合的手段,激发学生的学习兴趣,使学生获得成功的喜悦,提高学习热情.
1 巧妙利用多媒体形象展示数形之间的关系
抽象与复杂是高中数学的特点,在课堂上,假如只用教学语言来解释概念与规律,学生很难理解.因此在教学中,教师可借助多媒体来展示数学知识,通过动画的形式或者借助绘图工具来展现数学公式或者相关定理,将数学知识生动地展现给学生.例如在学习曲线运动相关的知识时,就可在多媒体上展现曲线的变化过程,帮助学生更好地理解与想象,找到解决问题的关键,由此培养学生的发散思维能力.在学习椭圆的参数方程中参数的几何意义与离心角的概念时,学生较容易产生混淆,此时教师就可借助方程、利用几何画板来画出图形,如图1所示.教师可拖动大圆上任一点,学生在观察不断变化的测量值时,就能够发现离心角的变化过程,进而从动态且直观的过程中体会到离心角的含义.
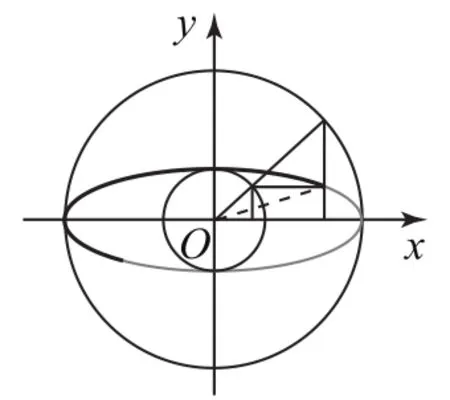
图1
2 结合教材内容,建立数形结合的解题思想
在数学课本中有很多知识包含了数形结合的内容.在教学中教师可按照教材内容灵活地选择典型命题,使学生运用数形结合法来解决问题,如此便可加深学生对数形结合思想的理解.例如在学习“平面解析几何初步”时,教师就可引导学生建立曲线与方程间和谐的对应关系,由此增强学生对几何图形的理解,进而更好地体现“数形结合”.又如在学习“2个变量的线性相关”内容时,教师可带领学生采取数形结合方法,将问题直观化,由此帮助学生构建知识框架.再如求函数值域时,教师可引导学生运用数形结合法来求解.
教师可引导学生按照题意画出函数图象,再进行观察,将其视为求斜率范围的问题.

如图2所示,可设动点P(cosx, sinx),定点A(2,0),将问题转化为求直线PA的斜率,进而降低了思维难度,答案为
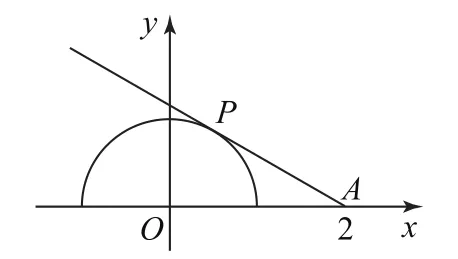
图2
此外,在学习正弦、余弦与正切值时,教师也可引导学生采用数形结合来解题.
例2 求5π/3的正弦、余弦与正切值.

可借助数形结合来解题,见图3.学生可在5π/3的终边取一点P(1,y),在Rt△PAO中,AO=1,可得出.在解题时借助图象画出辅助线AP就可帮助学生解答问题,由此提高解题效率.
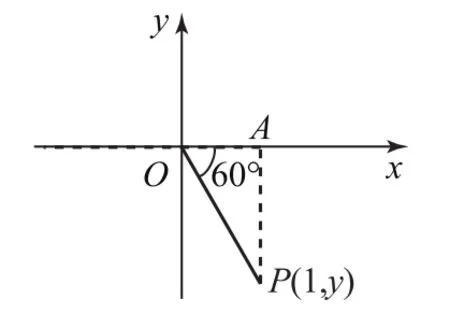
图3
3 利用直观图示理解抽象概念,体会数形结合的思想
在学生刚接触新的概念时,教师可借助图示来加强理解,带领学生体会数形结合思想.如在学习“集合”时,学生刚接触集合的概念,对于集合间的关系无法理解,此时教师便可借助图示来讲解.向学生介绍集合的另一种表达方式,即韦恩图,用封闭的曲线来表示集合,随后让学生思考2条封闭曲线能展示几种位置关系,并让学生画出来,如图4所示.
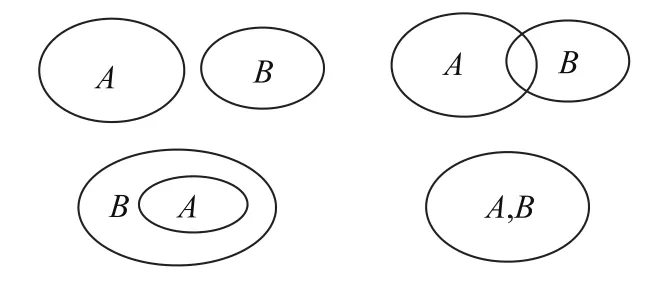
图4
让学生观察几种关系的相同点与不同点,并引导学生用集合语言来阐述,学生就能够轻松地了解“子集、真子集以及集合相等”的概念.
综上所述,“数形结合”是一种重要的思维形式,在高中数学教学中起到了非常重要的作用.应用数形结合法不仅能够帮助学生有效地解决数学问题,还能够激发学生的学习兴趣,提高学生的解题水平,促进学生的全面发展.
山东省邹平黄山中学)
