用导数研究函数的单调性

◇ 山东 彭庆柳张兆生

用导数研究函数的单调性

◇ 山东 彭庆柳1张兆生2

用导数求函数的单调区间或判断函数的单调性问题是本章的重点.解题时应注意如下几方面:

1)在利用导数讨论函数的单调区间时,首先要确定函数的定义域;

2)不能随意将函数的2个独立的单调递增(或递减)区间写成并集形式;

3)利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨论和数形结合思想的应用.

下面就具体题型进行剖析,希望对大家有所帮助.

1 利用函数的单调性比较大小

例1 定义域为R的函数f(x)对任意x都有f(2＋x)＝f(2－x),其导函数f′(x)满足则当2＜a＜4,有( ).

A f(2a)＜f(log2a)＜f(2);

B f(log2a)＜f(2)＜f(2a);

C f(2a)＜f(2)＜f(log2a);

D f(log2a)＜f(2a)＜f(2)

先根据条件求出函数的对称轴,再求出函数的单调区间,然后判定2、log2a、2a的大小关系,根据单调性比较f(2)、f(log2a)、f(2a)的大小即可.因为函数f(x)对任意x都有f(2＋x)＝f(2－x),所以函数f(x)的对称轴为x＝2.因为导函数f′(x)满足所以函数f(x)在(2,＋∞)上单调递减,(－∞,2)上单调递增.因为2＜a＜4,所以1＜log2a＜2＜4＜2a.又函数f(x)的对称轴为x＝2,所以f(2)＞f(log2a)＞f(2a),故选A.

本题主要考查了导数的运算,以及奇、偶函数图象的对称性和比较大小.根据导函数的符号确定函数的单调区间是解决此题的关键.最后利用函数的单调性比较函数值的大小,属于基础题.

2 借助导数研究不等式问题

由题意,要使对∀x1∈(0,2],∃x2∈[1,2],使得f(x1)≥g(x2)成立,只需fmin(x1)≥gmin(x2),且x1∈(0,2],x2∈[1,2],然后利用导数研究2个函数的最值即可.

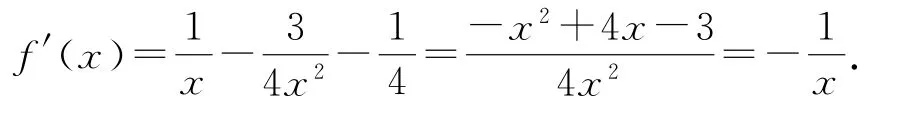
易知当x∈(0,1)时,f′(x)＜0,当x∈(1,2)时, f′(x)＞0,所以f(x)在(0,1)上递减,在[1,2]上递增,故fmin(x)＝f(1)＝1/2.

对于二次函数g(x)＝－x2－2ax＋4,该函数开口向下,在区间[1,2]上的最小值在端点处取得,所以要使对∀x1∈(0,2],∃x2∈[1,2],使得f(x1)≥g(x2)成立,只需fmin(x1)≥gmin(x2),即g(1)≤1/2或g(2)≤1/2,所以－1－2a＋4≤1/2或－4－4a＋4≤1/2,解得a≥－1/8,故选A.

本题考查了不等式恒成立以及有解问题的综合思路,概念性很强,注意理解.

3 已知单调性求参数范围

例3 已知函数f(x)＝x3－12x在区间(2m, m＋1)上单调递减,则实数m的取值范围是( ).

A －1≤m≤1; B －1＜m≤1;

C －1＜m＜1; D －1≤m＜1

由函数f(x)＝x3－12x在(2m,m＋1)内单调递减转化成f′(x)≤0在(2m,m＋1)内恒成立,得到关于m的关系式,即可求出m的范围.

因为f(x)＝x3－12x在(2m,m＋1)上单调递减,所以f′(x)＝3x2－12≤0在(2m,m＋1)上恒成立.所以即解得－1≤m＜1,故选项为D.

此题主要考查利用导函数的正、负判断原函数的单调性,属于基础题.

4 利用导数判断函数的图象

例4 函数y＝xf′(x)的图象如图1所示,则函数y＝f(x)的图象可能为( ).

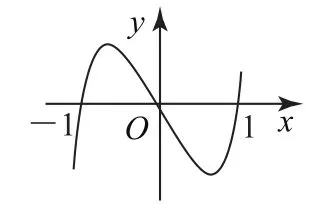
图1

由函数y＝xf′(x)的图象可知:当x＞1或x＜－1时,f′(x)＞0,f(x)在区间(－∞,－1)、(1,＋∞)上单调递增.

当－1＜x＜1时,f′(x)≤0,且只有x＝0时可能为0,f(x)在区间(－1,1)上单调递减.

根据以上结论可知函数f(x)的图象可能为C.

本题考查由导函数的图象判断原函数的单调性,充分利用图象提供的信息得出导函数的正、负是解题的关键.

5 利用导数研究函数的单调性

例5 已知函数f(x)＝(x＋1)lnx－a(x＋1) (a∈R)

(1)若当x∈[1,＋∞)时,f′(x)＞0恒成立,求a的取值范围;

(2)求函数g(x)＝f′(x)－a/x的单调区间.

(1)f′(x)＞0恒成立,即a＜lnx＋1/x＋1 (x≥1)恒成立.令h(x)＝lnx＋1/x＋1,则h′(x)＝所以h(x)在[1,＋∞)上是增函数,所以当x∈[1,＋∞)时,h(x)最小值＝h(1)＝2,故a＜2.

当a≥1时,g′(x)＞0,g(x)在(0,＋∞)上递增;

当a＜1时,由g′(x)＝0,得x＝1－a,x∈(0,1－a)时,g′(x)＜0,函数g(x)递减;x∈(1－a,＋∞)时,g′(x)＞0,函数g(x)递增.

熟练掌握利用导数研究函数的单调性的步骤、原理是解题的关键.解题中须注意含参数问题讨论.

1.山东省平邑第二中学2.山东省平邑曾子中学)