基于相对熵排序的装配序列质量模糊评价方法

张根保　罗冬梅　冉　琰　佘　林

重庆大学机械传动国家重点实验室，重庆，400030



基于相对熵排序的装配序列质量模糊评价方法

张根保罗冬梅冉琰佘林

重庆大学机械传动国家重点实验室，重庆，400030

在界定装配序列质量内涵的基础上，利用解释结构模型建立了可全面反映装配序列总体质量的评价指标体系，并利用各影响因素间的层次结构关系来定量计算各指标属性值。然后采用基于Vague集的模糊评判获得指标权重，同时引入基于相对熵的多属性排序方法对各装配序列质量进行综合评价，从而选出最优装配序列。最后用实例验证该方法的正确性与有效性。

装配序列；解释结构模型；相对熵；模糊评价

0　引言

装配序列评价是装配技术研究的重要环节，能否从数量众多的可行序列解空间中获得最佳装配序列，关键在于能否对可行序列进行准确、有效的综合性评价[1]。因此必须建立和健全装配序列评价指标体系，选择有效的评价方法，从中快速优选出最佳装配序列，从而实现装配序列规划技术的工程实用化。

目前已有大批学者对装配序列规划方法进行了研究：张嘉易等[2]针对装配的工艺性影响因素，采用整体性评价与单元级评价相结合的方法对产品装配序列进行评价；王孝义等[3]构建了一个指标较为完备的装配序列质量三层评价体系，采用基于有向图序列比较方法，实现装配序列基础指标下的自动评价；周开俊等[4]提出了客观自适应熵权法与模糊集相结合的产品装配序列评价方法；袁宝勋等[5]利用产品三维模型与仿真数据，建立了基于区间逆序数和逼近理想解法的装配序列评价模型；马红占等[6]考虑到装配序列与工人之间的影响关系，提出了基于人因仿真分析的装配序列评价方法；Lazzerini等[7]采用的遗传算法利用随机初始化种群的方式来求解最优装配序列。以上算法多以获得最小的装配时间或最高的工作效率为优化目标，但是从装配可靠性、装配质量等方面来看，这种优化目标并不能保证装配后的产品可靠性和质量最优。

由于产品质量和可靠性在很大程度上是由装配过程来保证的，因此，在评价装配序列时，必须考虑质量和可靠性的保证情况。现有的层次结构评价指标体系的提出缺乏科学依据，因此本文首先引入解释结构模型(interpretative structure model，ISM)，从装配序列零件级和序列级影响因素出发，构建了一个指标较为完备、科学的装配序列质量评价体系，并在此基础上利用各因素间的层次结构影响关系定量计算指标属性值，从而使评价结果更具有理论依据。然后采用基于Vague集的模糊评判计算指标权重，同时引入基于相对熵的排序方法[8]对各可行装配序列进行综合评价，从而建立可有效反映各序列本质差异的装配序列总体评价模型。

1　基于ISM的装配序列质量影响因素分析

解释结构模型是Warfield为分析复杂的社会经济系统结构而提出的一种结构建模方法，其主要特点是应用有向图与矩阵理论，对复杂系统的各组成要素(或子系统)间的结构关系加以描述，使系统中各要素间复杂、零乱的关系层次化、条理化[9]。其主要构建流程为：首先通过调查分析确定系统的影响因素及其相互间的关系，依次建立各因素的邻接矩阵和可达矩阵；然后经过相应的矩阵演算与变换对这些相互关系进行划分，明确系统要素的层次与结构，从而建立影响因素的解释结构模型图[10]。

引入解释结构模型对装配序列质量影响因素进行分析，可以理清不同装配序列装配质量的影响机制，并根据模型结果确定影响装配序列最直接、最基本的因素，从而为不同装配序列的质量评价提供决策参考。

通过对大量制造企业进行调研分析，提取出15个装配序列质量影响因素：装配体质量S1、装配单元对称性S2、连接类型S3、装配关系数S4、零件参与装配尺寸链数量S5、基准方向变换次数S6、重力方向装配次数S7、重定向次数S8、装配操作并行性S9、装配操作聚合性S10、装配性能稳定性S11、装配过程可靠性S12、装配精度保证性S13、装配工艺简单性S14、装配成本经济性S15。

为了分析上述因素对装配序列质量的影响，建立解释结构模型，首先建立装配过程质量影响因素邻接矩阵，用以描述各因素间直接相互关系，则定义其邻接矩阵：

(1)

p，q=1，2，…，15

根据装配过程质量控制的工程实际和同行业专家的观点，确定各因素间的相互影响关系，建立影响装配序列质量相关因素的邻接矩阵A=[ap，q]15×15，其中，a1,11=a1,12=a1,14=a2,8=a2,14=a3,5=a3,11=a3,13=a3,14=a4,13=a5,13=a5,14=a6,8=a6,12=a6,14=a7,13=a8,11=a8,14=a8,15=

a9,15=a10,14=a10,15=1，其他元素的值为0。

对邻接矩阵A与单位矩阵I的和进行基于布尔代数的幂运算，直到矩阵中不再产生新的间接关系(矩阵中不再产生新的元素1)为止，得到影响因素的可达矩阵M(可达矩阵中元素为1表示因素Sp到Sq之间存在着可到达路径)。

M=(A+I)r+1=(A+I)r≠…≠

(A+I)2≠(A+I)

(2)

r=1,2,…

经计算得r=2，M=[mi,j]15×15=(A+I)2，其中，m1,11=m1,12=m1,14=m2,8=m2,14=m3,5=m3,11=m3,13=m3,14=m4,13=m5,13=m5,14=m6,8=m6,12=m6,14=m7,13=m8,11=m8,14=m8,15=m9,15=m10,14=m10,15=1，其他元素的值为0。

然后按照解释结构模型方法对可达矩阵进行层次化处理和级别划分[11]，得出装配序列质量影响因素(可分为三层，第一层为装配性能稳定性S11、装配过程可靠性S12、装配精度保证性S13、装配工艺简单性S14、装配成本经济性S15，第二层为装配体质量S1、装配关系数S4、零件参与装配尺寸链数量S5、重力方向装配次数S7、重定向次数S8、装配操作并行性S9、装配操作聚合性S10，第三层为装配单元对称性S2、连接类型S3、基准方向变换次数S6)。最后根据所得结果，采用有向图的形式画出装配序列质量影响因素的解释结构模型。由图1可得，装配性能稳定性S11、装配过程可靠性S12、装配精度保证性S13、装配工艺简单性S14、装配成本经济性S15是影响装配序列质量的第一级要素，也是影响其质量的最直接原因，其中，装配性能稳定性主要受第二层中装配关系数S4、零件参与尺寸链数量S5、重力方向装配次数S7影响，而影响重定向次数S8的根本原因是装配单元对称性S2和基准方向变换次数S6。因此为了从整体上对装配序列质量进行综合评价，选取结构模型第一层影响因素作为评价指标体系，即

V={V1，V2，V3，V4，V5}={S11，S12，S13，S14，S15}={装配性能稳定性，装配过程可靠性，装配精度保证性，装配工艺简单性，装配成本经济性}

图1　装配序列质量影响因素的解释结构模型

2　评价指标计算方法

2.1装配性能稳定性

装配性能稳定性指在装配过程中，装配序列在装配力、重力作用下及各类连接关系下保持稳定的能力，主要与零件配合类型、零件装配关系数等因素有关。为了评价整个装配序列在产品加工过程中的稳定程度，常采用综合工序能力指数来衡量其稳定性。工序能力指数用来衡量工序能力满足规定质量要求的程度，是工序处于稳定受控状态时，加工出来的产品质量满足技术规范要求的能力[12]，常用装配过程中产品轴孔位特征值的变异和波动来表示，即

(3)

式中，CPk为工序能力指数；T为产品轴孔位特征的公差范围；μ、σ分为工序质量特性值的期望和标准差；μ0为轴孔位特征的标称值。

设装配序列由n道工序组成，CPki为第i道工序的工序能力指数，根据不同工序在对最终装配质量影响程度的不同，按照Satty1-9标度法[13]计算不同工序的权重值ζi，则定义其综合工序能力指数为

(4)

2.2装配过程可靠性

装配过程可靠性是指按照给定的装配序列在规定条件下和规定的时间内，保证装配出来的产品具有规定可靠性水平的能力[14]。借鉴可靠性工程理论，在分析装配序列各工步之间关系的基础上，运用GO法建立其装配过程的GO图，通过GO法运算法则，求得不同装配序列装配过程的最终可靠度[15-16]。GO法采用操作符代替单元功能和特性，信号流表示系统单元的输入和输出以及单元之间的关联，所有操作符的正常概率数据可由装配多次的各正常异常次数与总装配次数之比得到,因此装配序列的最终可靠度为

(5)

式中，PRi(0)为输入操作符输出信号正常的状态概率；Pci(0)为操作符的正常状态概率，状态值0表示工步正常；m为输入操作符的个数；η为操作符个数。

2.3装配精度保证性

装配过程中，不同几何可行装配序列的精度保证性主要受装配过程重定向次数、装配体对称性等因素影响，保证装配精度的主要目的是使装配产品误差最小化。由于产品的精度指标是在制造过程中随着轴孔位特征的装配逐步实现的，且多工序装配中存在工艺自修正性，即前序工序的误差可以在后序工序予以修正，从而使精度在一定程度上得到保证，因此定义工艺自修正系数来表示装配过程的精度保证性。选取装配过程中Q个关键孔位特征的精度样本，考虑到装配过程中可能存在自修正能力提高的趋势，因此定义整个装配过程的工艺自修正系数为

(6)

j=1，2，…，n

式中，di1、din分别表示装配过程中首尾工序的装配误差；Di(j)为第i个轴孔位特征的第j个装配工序对第j-1个工序装配误差的修正量，Di(j)=|di(j-1)-dij|。

2.4装配工艺简单性

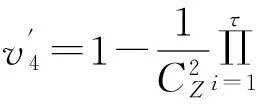
(7)

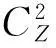
2.5装配成本经济性

(8)

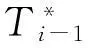
3　指标权重的确定

装配序列质量的评价过程中，各个影响因素对质量的影响不同，因此需要对各个因素分别赋予权重系数，以对其重要程度进行量化。在确定指标权重时，样本数据缺乏，各指标之间具有一定的模糊性，因此需要充分利用专家群体决策来计算各指标权重。为了增加结果的准确性与可信性，采用基于Vague集的模糊理论，综合专家的支持、反对意见，从而更加全面地表达模糊信息，使得权重确定更具有合理性和可操作性。

Vague集是模糊集的推广形式，其定义[17]为

其中，tB(χ)是从支持χ的证据所导出的χ隶属度的下界，fB(χ)是从反对χ的证据所导出的χ非隶属度的下界，且tB(χ)+fB(χ)≤1。基于Vague集的指标权重确定方法如下所示。

(1)首先设置赋权评分等级及其基准分值，设评分等级集为

χ={χ1，χ2，…，χN}

式中，χj为第j个评分等级的基准分值，j=1，2，…，N；N为评分等级数。

因素的权重由G位专家按照表决模型综合投票决定，用Vague值表示。将因素Vi的权重属于评分等级χj的可能范围表示为

Γij={[tij(χ)，1-fij(χ)]；αij}

(9)

i=1，2，…，Θ

式中，Θ为评价指标数目；αij为弃权者倾向于改投赞成票的可能性，称为倾向性因子。

(2)计算Lij的满意度，即估算Lij所表征的模糊隶属度，得到其估算值：

Lij(χ)=tij(χ)+αij(1-tij(χ)-fij(χ))

(10)

(3)计算因素的基本权重。为了综合考虑专家的决策信息，这里采用加权平均法，即将估算值Lij(χ)作为权数，对各个评分等级χj进行加权平均得因素Vi的基本权重：

(11)

(4)对基本权重ρi进行归一化处理，得到权重集W={w1，w2，…，wΘ}，且

(12)

4　基于相对熵的综合评价模型

产品装配序列质量评价不仅是装配序列规划的关键内容，也是装配工艺的重要环节，因此在定量评价各个指标对装配质量影响的基础上，还需对各指标进行集成，以实现对装配序列质量的综合评价。引入基于相对熵的排序方法，利用被评序列与理想序列和负理想序列的相对熵来集成不同的影响因素，从而实现对不同装配序列质量的综合评价。

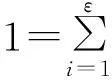
(13)

其中，H为X相对于Y的相对熵，当X=(x1，x2，…，xε)和Y=(y1，y2，…，yε)的离散概率分布完全相同时，X相对于Y的相对熵达到最小值，即相对熵越小，概率分布越相似，因此可以用相对熵来度量两者的符合程度。采用相对熵的多属性决策来对装配序列的质量进行评价的具体步骤如下：

(1)建立几何可行装配序列方案集E={E1，E2，…，Ee},其中，e为装配序列个数，在定量计算评价指标后，得到不同装配序列各指标属性值V=[vij]e×Θ，其中，vij表示第i(i=1，2，…，e)个序列关于第j(j=1，2，…，Θ)个指标的评价值。为消除不同指标间量纲的差异，对极大型指标VU和极小型指标VL属性值分别进行量纲一化处理：

(14)

(2)计算加权后的标准化决策矩阵

γ=[γij]e×Θ

(15)

(3)针对极大型指标和极小型指标确定分别其理想序列方案和负理想序列方案

(16)

(4)根据相对熵计算公式分别计算装配序列与理想序列方案与负理想序列方案的相对熵：

(17)

(5)计算各装配序列对理想序列方案的相对贴近度

(18)

5　案例分析

以图2所示的某型张紧辊(共有18个零件)装配为例，验证所提方法的正确性与有效性。采用本文所提装配序列评价方法，对该部件的3个可行装配序列(图3)进行综合评价，具体评价步骤如下。

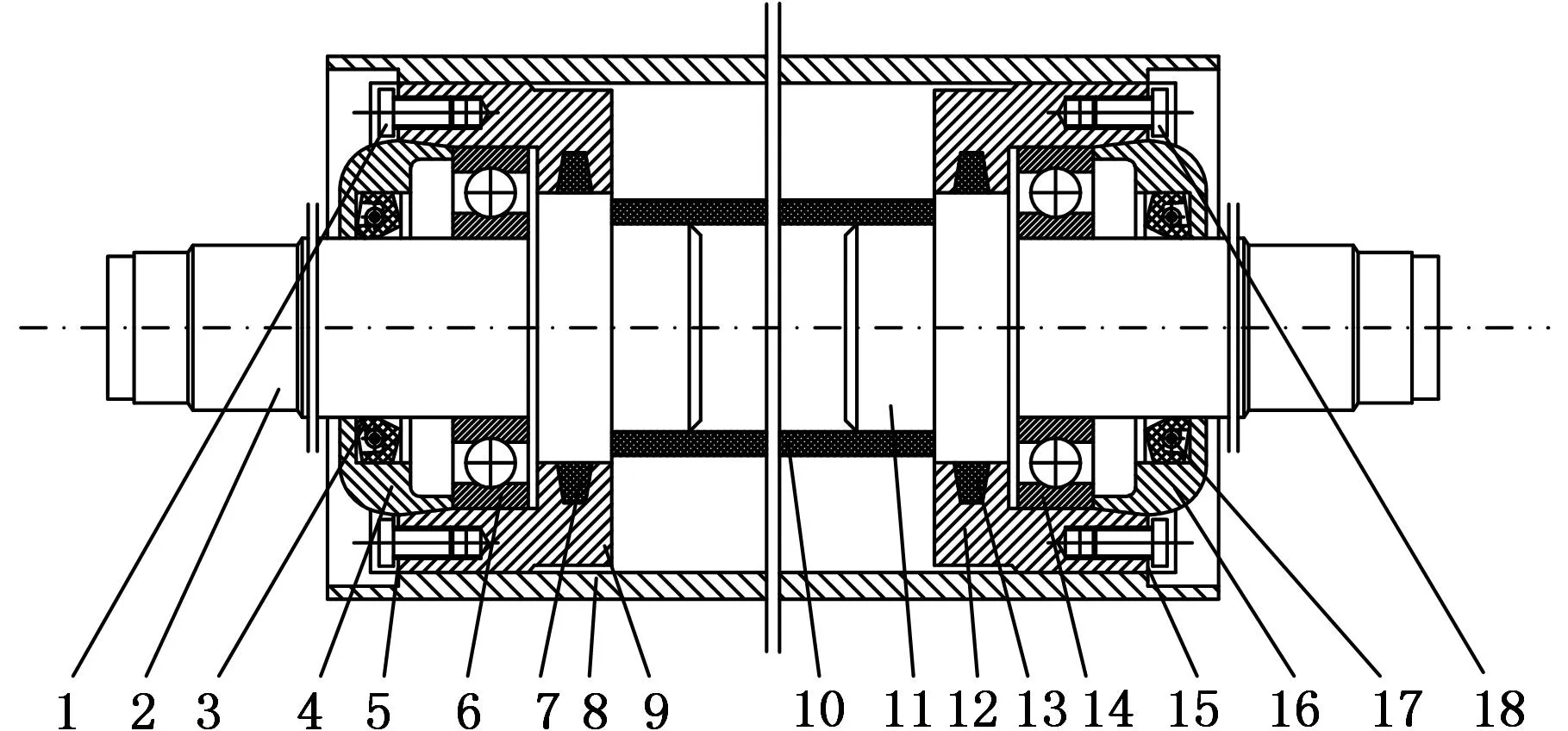
1.螺钉　2.张紧辊轴头　3.骨架油封　4.透盖　5.垫圈　6.轴承　7.毡圈　8.张紧辊筒　9.辊筒端盖　10.心轴管　11.张紧辊轴头　12.辊筒端盖　13.毡圈　14.轴承　15.垫圈　16.透盖　17.骨架油封　18.螺钉

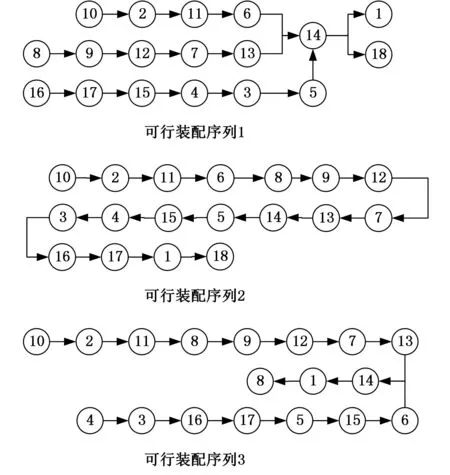
图3　张紧辊可行装配序列

(1)针对图3中张紧辊的3个可行装配序列，建立装配序列评价方案集E={E1，E2，E3}，利用第2节中的评价指标计算方法求得各装配序列指标属性值。装配性能稳定性、装配过程可靠性、装配精度保证性属于极大型指标，装配工艺简单性、装配成本经济性属于极小型指标，按照式(14)进行数据量纲一化处理，其具体结果如表1所示。

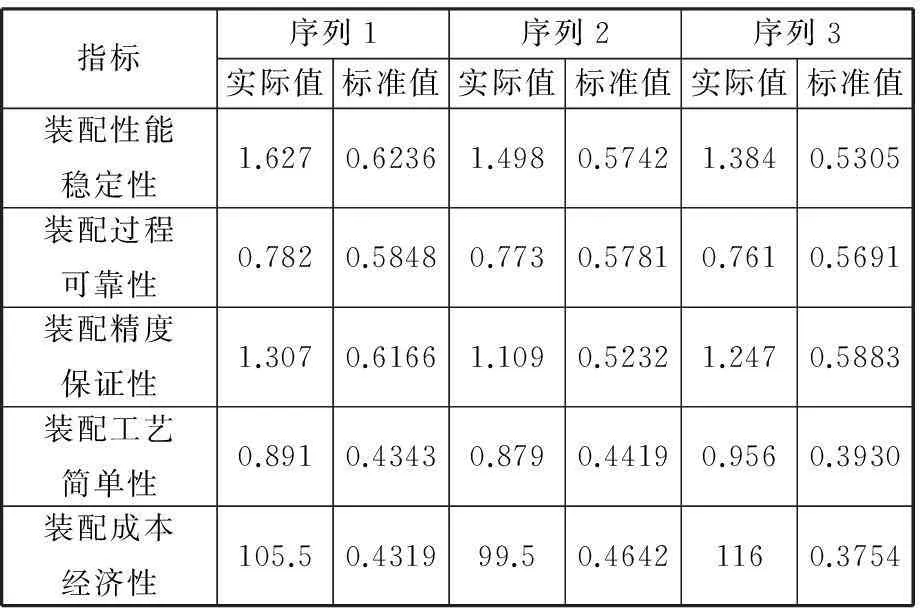
表1　指标属性值数据处理

(2)确定评价指标权重。首先设置评分标准，这里将赋权的基准评分等级设为四级，按照一般、较重要、重要、很重要4个等级赋予相应的基准分值，即χ={χ1，χ2，χ3，χ4}={2，4，6，8}。邀请了20位专家，包括4位企业领导、8位技术人员和8位科研人员，分别对各指标权重进行了经验赋值，综合评判结果可得

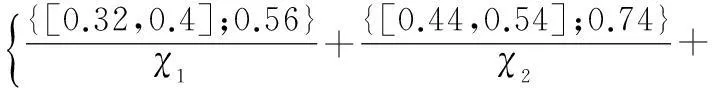
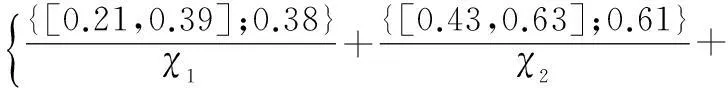
由式(10)计算得

L1={0.1，0.3325，0.672，0.448}

L2={0.1780，0.4220，0.3516，0.2326}

L3={0.261，0.4458，0.4068，0.227}

L4={0.3648，0.514，0.2636，0.1236}

L5={0.2784，0.5520，0.3732，0.178}

将L1～L5的值代入式(11)可计算5个评价指标的基本权重：ρ1=5.891 14，ρ2=5.078 87，ρ3=4.894 82，ρ4=4.230 65，ρ5=4.652 58，对基本权重值进行归一化处理得指标权重集：

W={0.2381，0.2051，0.1977，0.1710，0.1881}

(3)将指标权重代入式(15)求得标准决策矩阵:

再针对极大型指标和极小型指标确定分别其理想序列方案和负理想序列方案，即

γ+={0.1485，0.1199，0.1219，0.0672，0.0706}

γ-={0.1262，0.1163，0.1034，0.0756，0.0873}

(4)最后根据式(17)、式(18)计算各方案与理想序列方案的相对熵，进而求得相对贴近度，根据相对贴近度的大小比较获得序列排序。

根据表2所示的评价结果可得装配序列1的质量最优，序列3次之，序列2质量最差，因此选择装配序列1进行装配时产品质量更优。

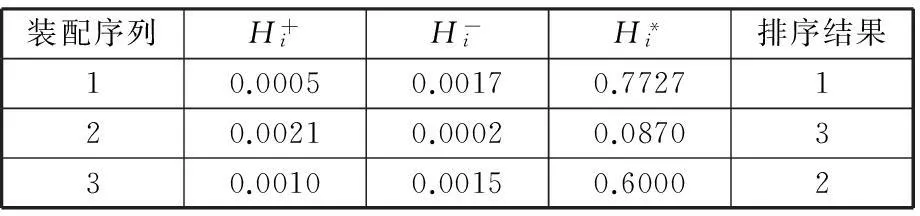
表2　基于相对熵集成的排序结果

6　结语

本文综合考虑了影响装配序列总体质量的各种因素，运用解释结构模型建立了包含过程可靠性这一关键要素的评价指标体系；在定量计算各指标属性值的基础上，引入了基于Vague集的模糊评价来综合专家的支持和反对意见，使指标权重的计算结果更加可靠；建立了可有效反映各序列本质差异的装配序列总体评价模型，实现了对不同装配序列的综合评价。

[1]顾延权，高国安，徐向阳. 装配工艺规划中装配序列生成与评价方法研究[J].计算机集成制造系统，1998, 4(1): 25-27.

GuTingquan,GaoGuo’an,XuXiangyang.StudyontheApproachforGenerationandEvaluationofAssemblySequencesforAssemblyProcessPlanning[J].ComputerIntegratedManufacturingSystems, 1998,4(1): 25-27.

[2]张嘉易, 王成恩, 马明旭, 等. 产品装配序列评价方法建模[J]. 机械工程学报, 2009,45(11): 218-224.

ZhangJiayi,WangChengen,MaMingxu,etal.ModelingofTheMethodofProductAssemblySequenceEvaluation[J].JournalofMechanicalEngineering, 2009,45(11): 218-224.

[3]王孝义, 张友良, 张帆. 装配序列评价研究[J]. 中国机械工程, 2006,17(13): 1165-1169.

WangXiaoyi,ZhangYouliang,ZhangFan.ResearchonEvaluatingAssemblySequence[J].ChinaMechanicalEngineering， 2006,17(13): 1165-1169.

[4]周开俊, 李东波, 许焕敏. 一种产品装配序列的评价方法[J]. 计算机集成制造系统, 2006,12(4): 563-567.

ZhouKaijun,LiDongbo,XuHuanmin.EvaluationApproachtoProductAssemblySequences[J],ComputerIntegratedManufacturingSystems, 2006,12(4): 563-567.

[5]袁宝勋, 褚学宁, 李玉鹏，等. 基于产品设计数据的装配序列定量化评价方法[J]. 计算机集成制造系统, 2014, 20(4): 807-816.

YuanBaoxun,ChuXuening,LiYupeng,etal.QuantitativeEvaluationApproachforAssemblySequencesBasedonProductDesignData[J].ComputerIntegratedManufacturingSystems, 2014, 20(4): 807-816.

[6]马红占，褚学宁，刘振华，等.基于人因仿真分析的装配序列评价模型及应用[J].中国机械工程, 2015, 26(5): 652-657.

MaHongzhan,ChuXuening,LiuZhenhua,etal.AssemblySequenceEvaluationModelingandApplicationBasedonHumanFactorSimulationAnalysis[J].ChinaMechanicalEngineering, 2015, 26(5):652-657.

[7]LazzeriniB,MarcelloniF.AGeneticAlgorithmforGeneratingOptimalAssemblyPlans[J].ArtificialIntelligenceinEngineering, 2000, 14(4): 319-329.

[8]赵萌，邱寇华，刘北上.基于相对熵的多属性决策排序方法[J].控制与决策，2010,25(7)：1098-1100.

ZhaoMeng,QiuKouhua,LiuBeishang.RelativeEntropyEvaluationMethodforMultipleAttributionDecisionMaking[J].ControlandDecision, 2010, 25(7):1098-1100.

[9]汪应洛. 系统工程理论、方法与应用[M]. 北京:高等教育出版社，1998.

[10]邱青安，高洪达，崔利荣. 基于解释结构模型的我国载人航天发展影响因素研究[J]. 数学的实践与认识，2015, 45(12): 60-70.

QiuQing’an,GaoHongda,CuiLirong.ResearchonInfluencingFactorsofChina’sMannedSpaceDevelopmentBasedonInterpretativeModel[J].MathematicsinPracticeandTheory, 2015,45(12):60-70.

[11]刘家国，姜兴赫，赵金楼，基于解释结构模型的供应链弹性系统研究[J]. 系统管理学报，2015,24(7)：617-623.

LiuJiaguo,JiangXinghe,ZhaoJinlou.ResilienceoftheSupplyChainSystemBasedonInterpretativeStructureModeling[J].JournalofSystem&Management, 2015,24(7)：617-623.

[12]贾新章，曾志华. 从工序能力分析到6σ设计[J]. 电子产品可靠性与环境试验，2002,6(3)：31-34.

JiaXinzhang,ZengZhihua.FromProcessCapabilityAnalysisto6σDesign[J].ElectronicProductReliabilityandEnvironmentalTesting, 2002,6(3)：31-34.

[13]骆正清，杨善林. 层次分析法中几种标度的比较[J].系统工程理论与实践，2004(9):51-60 .

LuoZhengqing,YangShanlin.ComparativeStudyonSeveralScalesinAHP[J].ChineseJournalofSystemsEngineering-Theory&Practice，2004(9): 51-60.

[14]金伟娅，张康达.可靠性工程[M].北京：化学工业出版社,2005.

[15]张根保，葛红玉.GO法在产品装配过程质量分析中的应用研究[J]. 中国机械工程，2010,21(22)：2689-2692.

ZhangGenbao,GeHongyu.ApplicationandResearchofGOMethodologyinQualityAnalysisofProductAssemblyProcesses[J].ChinaMechanicalEngineering, 2010, 21(22)：2689-2692.

[16]刘林林，任羿，王自力，等. 基于贝叶斯网络的GO法模型算法[J]. 系统工程与电子技术，2015，37(1)：212-218.

LiuLinlin,RenYi,WangZili.AlgorithmBasedonBayesianNetworkforGoMethodology[J].SystemEngineeringandElectronics, 2015，37(1)：212-218.

[17]赵德孜. 机械系统设计初期的可靠性模糊预计与分配[M]. 北京：国防工业出版社.2010.

[18]KullbackS,LeiblerRA.OnInformationandSufficiency[J].AnnalsofMathematicStatistics, 1951, 22(1): 79-86.

[19]程发新，程栋. 基于相对熵的残缺语言判断矩阵群排序方法[J]. 控制与决策，2015，30(3):479-484.

ChengFaxin,ChengDong.GroupRankingBasedonRelativeEntropywithIncompleteLinguisticJudgmentMatrices[J].ControlandDecision. 2015，30(3):479-484.

(编辑张洋)

Fuzzy Evaluation of Assembly Sequence Quality Based on Relative Entropy Method

Zhang GenbaoLuo DongmeiRan YanShe Lin

The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030

Based on the definition of assembly sequence quality, an evaluation system was firstly established to present comprehensive quality of assembly sequences by interpretative structure model, and the index attribute values were calculated quantitatively. Then in order to get index weights, the Vague set was used to concentrate experts’ opinions. Finaly, a new decision-making method was founded based on entropy theory, which was supported for alternative assessments with large difference, to evaluate comprehensive quality of all feasible assembly sequences. Case study indicates the rationality and effectiveness of this method.

assembly sequence; interpretative structure model; relative entropy; fuzzy evaluation

张根保，男，1953年生。重庆大学机械传动国家重点实验室教授、博士研究生导师。主要研究方向为现代质量工程、先进制造技术、可重构制造装备和企业信息化等。获得省部级科技成果一等奖1项、二等奖2项。发表论文250余篇，出版专著作4部。罗冬梅，女，1990年生。重庆大学机械工程学院及重庆大学机械传动国家重点实验室硕士研究生。冉琰，女，1988年生。重庆大学机械传动国家重点实验室博士研究生。佘林，男，1988年生。重庆大学机械传动国家重点实验室硕士研究生。

2015-06-16

国家自然科学基金资助项目(51175527)；国家科技重大专项(2013ZX04012-041，2014ZX04001-031)

TH162

10.3969/j.issn.1004-132X.2016.08.017