基于非负矩阵分解的产品结构相似性判断及其应用
2016-08-16徐新胜
徐新胜 王 诚 肖 颖
中国计量学院,杭州,310018
基于非负矩阵分解的产品结构相似性判断及其应用
徐新胜王诚肖颖
中国计量学院,杭州,310018
为了快速发现可重用产品结构,提出了基于非负矩阵分解的产品结构相似性判断方法。通过将产品结构邻接矩阵转化为邻接向量,构建包含全部结构信息的库矩阵;利用Multiplicative Updates(MU)算法对库矩阵进行非负矩阵分解,实现以低维空间向量描述的产品结构;在此基础上,通过计算低维向量的欧氏距离,可以判断产品结构之间的相似性;最后通过实例对所提出原理和方法进行了验证,结果表明,该方法比目前的相似性判断方法更高效。
产品结构;非负矩阵分解;相似性;欧氏距离
0 引言
大规模定制生产中,针对客户定制的产品,从企业的产品库中找到相似的模型或产品结构,加以充分利用,可以降低定制企业的成本、缩短交货期。因此,相似性研究受到了国内外专家与学者的广泛关注。成组技术[1]是一种传统的相似性分析方法,通过分类编码将零件归类,或将产品结构归为一族。此外,基于功能特征的相似性分析[2-3]和面向形状的相似性分析[4-7]在设计、制造领域也得到了应用。
产品结构是企业在长期设计、制造过程中形成的结构性数据,能够体现出复杂产品的零部件组成情况与关联关系[8],所以,以此为对象的相似性研究也逐渐引起了关注。丘宏俊等[9]基于XML文档结构相似性判定方法,提出了综合结构操作类型及其成本、节点位置等信息的产品结构相似性计算模型,并在飞机制造中得到应用。Romanowski等[10]基于产品结构,提出了最小加权对称差的分析方法,将一类无序的产品结构树归类到产品族中。Tsai等[11]提出了基于构件匹配算法和模糊模式组合的产品结构相似性判定方法。
然而,上述方法在研究产品结构相似性时,并没有考虑产品结构中节点之间的数量约束关系。对此,Shih[12]提出了基于正交Procrustes分析的产品结构相似性判定方法,并将其应用于产品结构聚类。但这种方法需要对产品结构的邻接矩阵进行奇异值分解,因此,在产品中零部件较多时,将会导致计算过程步骤多、计算量大,其实用性受到一定限制,并且处理过程比较抽象,无法直观地反映产品之间的相似性关系。
非负矩阵分解算法具有易于实现、存储空间小,而且能够有效地保持数据的非负性等特点[13],本文基于此提出产品结构相似性判定方法,目的是在简化计算步骤的基础上,进一步提高相似性判定的高效性,丰富相似性计算结果的内涵。
1 产品结构相似性与非负矩阵分解
1.1产品结构描述及其相似性分析
通常,产品采用具有层次的结构来描述。产品结构中,节点表示产品部件或者零件,边表示零部件之间的装配或者隶属关系,如图1所示,从上到下,同一条边上面的点代表父件,下面的点称为子件,图1中的部件a既是c的父件,又是o的子件。边旁边的数字表示生产单位父件时所需子件的数量。

图1 产品结构
对于图1描述的产品结构,其对应的邻接矩阵如下:
oabcdefghi

大规模定制生产中,针对客户的产品定制需求(通常对应一个虚拟的产品结构),怎样从定制企业的产品库中找到最合适的产品实例或者产品模型,充分重用其零部件在设计、制造、质量、管理等方面的数据和信息,对于降低大规模定制产品的生产成本、缩短交货期,具有重要的意义。
通常,企业的产品库中会有多个产品实例或者模型待选,对这些产品实例或模型进行统一比较,依照相似性大小排序,可以有效简化产品结构相似性分析和计算过程,提高效率。为实现这个目标,本文提出基于非负矩阵分解(non-negative matrix factorization,NMF)的产品结构相似性判定方法。

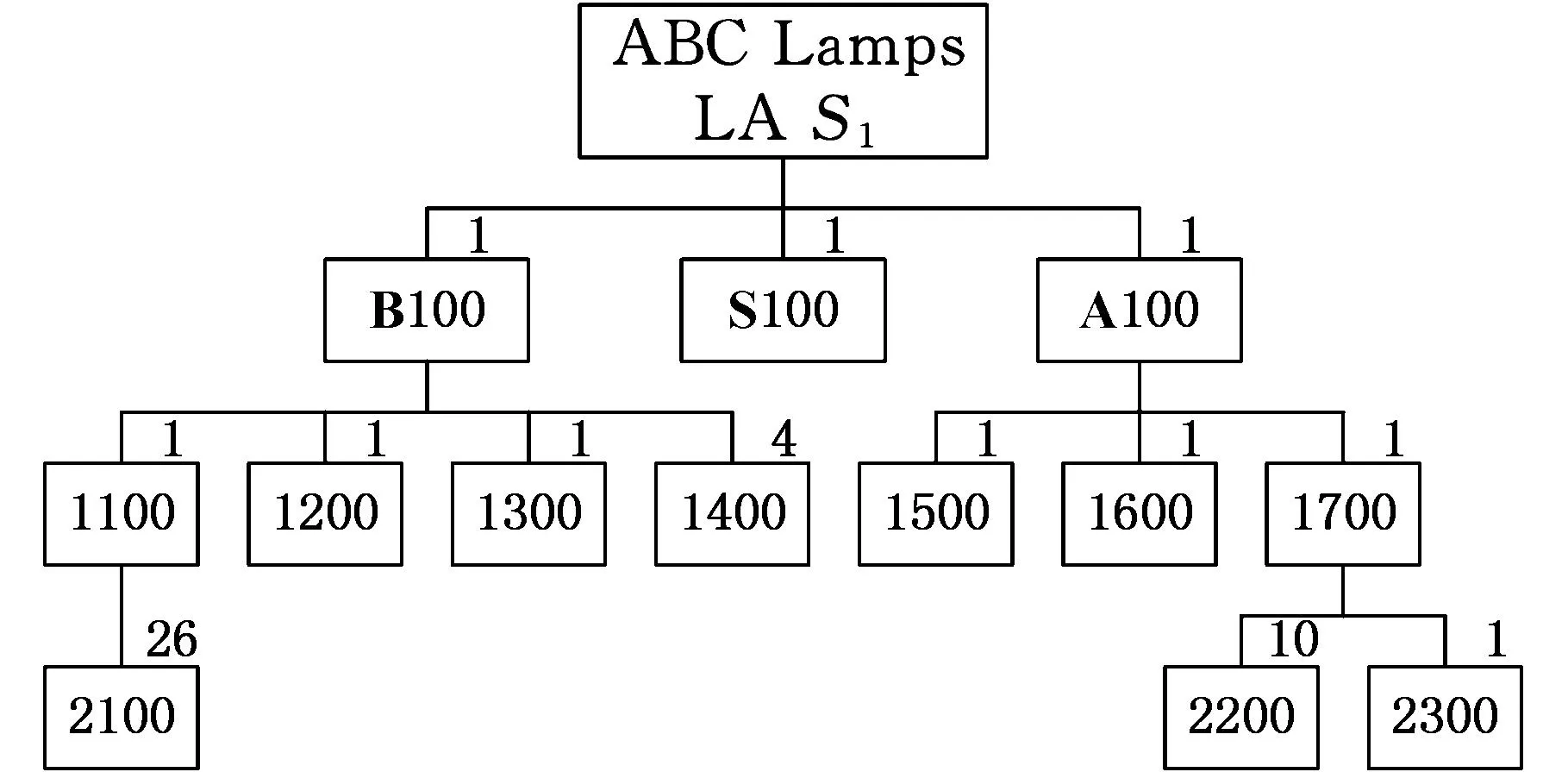
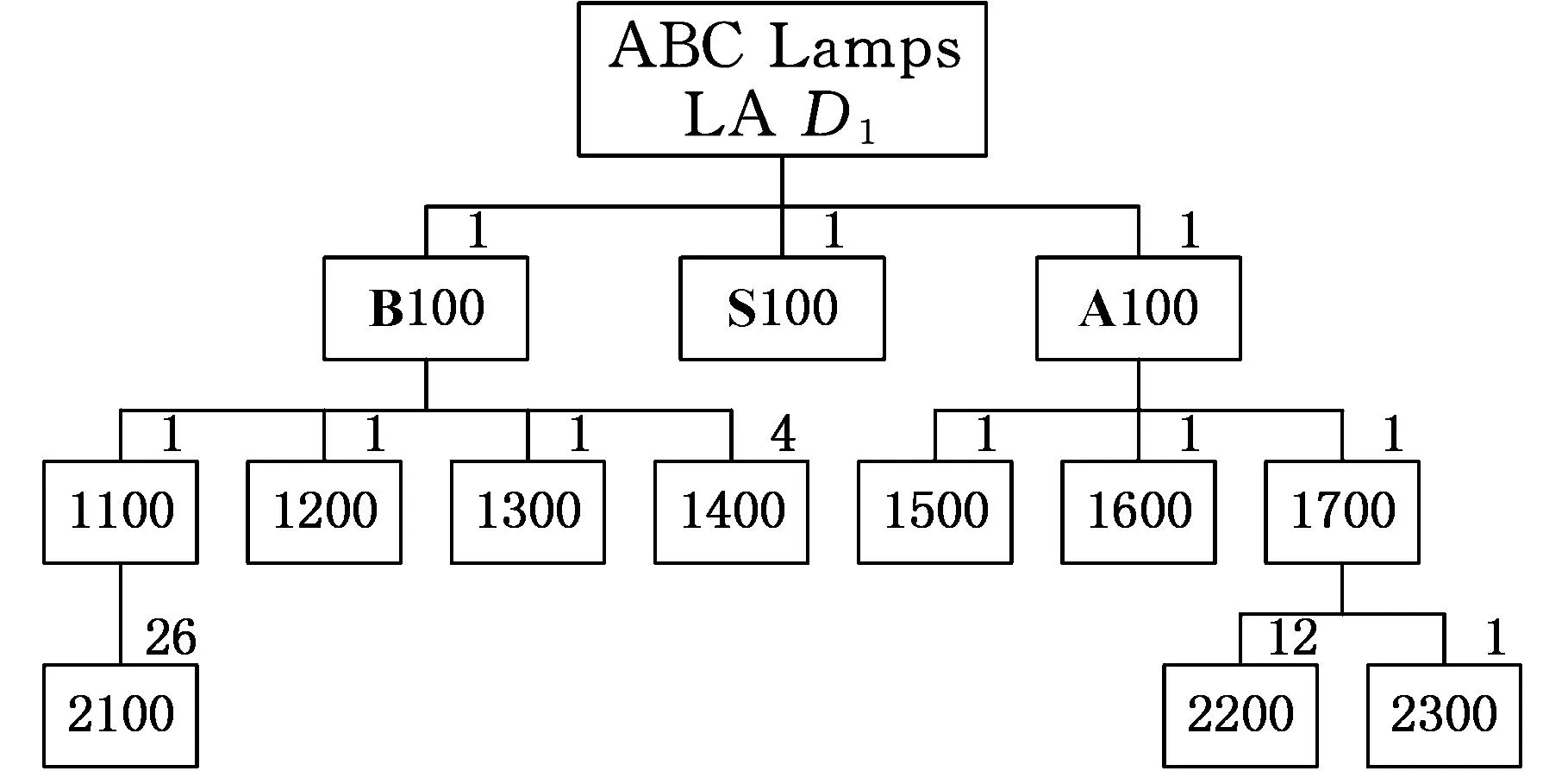
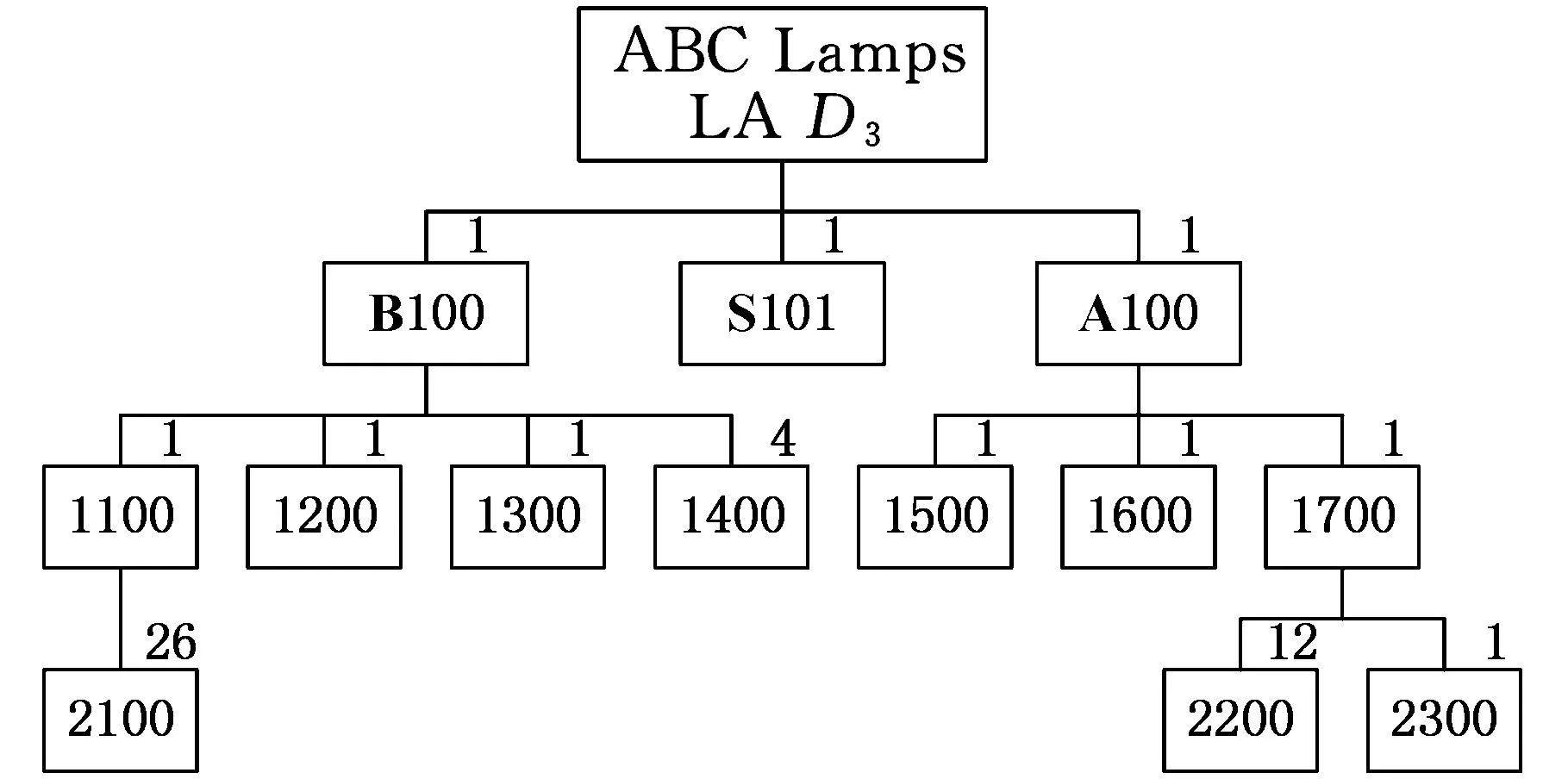
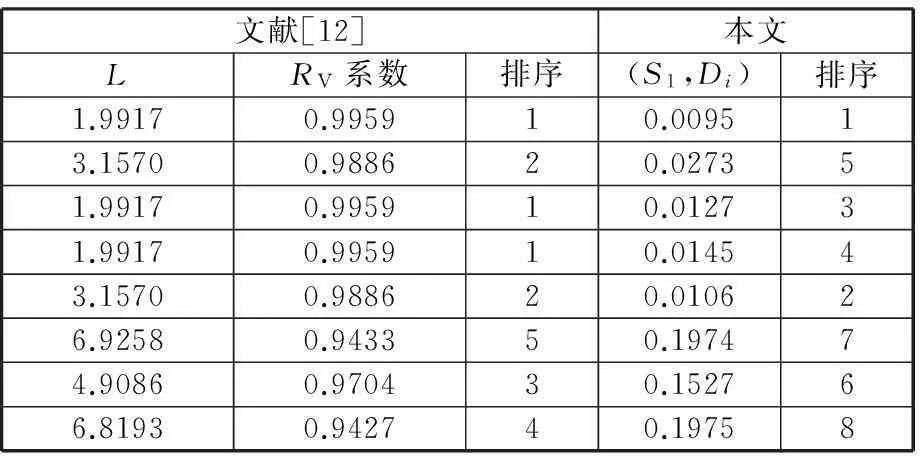
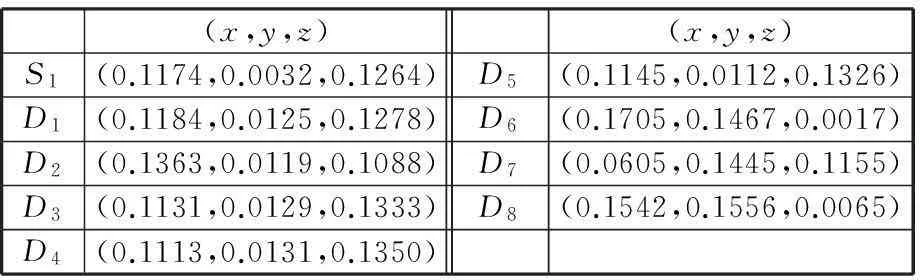
其中,P(*,k)为矩阵P的第k个列向量;qki是矩阵Q的第k行第i列的元素。上述等式表明βi被从m2维的空间映射到r维空间中(m2 产品结构被定量地表示到这个低维空间中,于是,通过计算目标产品结构与各查询产品结构对应的低维向量之间的距离便可以来判断产品结构相似性。 1.2非负矩阵分解基本原理 非负矩阵分解最初由Paatero等[14]于1994年提出,现在已在文本分类、图像分析、复杂网络等方面得到广泛应用,与其他矩阵分解(奇异值分解、特征值分解)类似,非负矩阵分解也实现了线性的维数约简,但要求分解后的所有分量均为非负实数,这种分解方式符合直观理解:整体是由部分组成的[15]。因此,它能够在某种意义上抓住产品结构数据的本质[13],这种特性表明,采用非负矩阵分解后的降维数据保留了原有产品结构的本质特征。 下面对非负矩阵分解问题的基本原理进行说明。不失一般性,假设G=[gij]p×q(gij>0)是任意给定的非负矩阵,非负矩阵分解算法的目标便是寻找两个非负矩阵Wp×r=[wij]p×r和Hr×q=[hij]r×q,使得 Gp×q=[γ1γ2…γq]p×q=WH= (1) 其中,矩阵G首先表示为列向量的形式,γi为组成矩阵G的第i列向量(i=1,2,…,r)。 当原有矩阵G的各列即γi线性无关时,以这q个向量为基可以张成一个线性空间Vq。非负矩阵分解的运算就是把γi从q维线性空间Vq映射到W各列向量张成的r维线性空间Vr中。设 实际计算中,非负矩阵分解问题可以描述成数学模型: (2) 式中,‖*‖F为矩阵的F-范数。 基于Multiplicative Updates(MU)算法[16],W和H分别计算如下: (3) (4) 其中,(GHT)ia表示矩阵G和HT相乘后,所得矩阵的第i行第a列元素。式(3)、式(4)描述了一个迭代-更新过程,即每一次更新W和H中的元素,均利用原有的W和H进行运算,研究表明,这种算法是收敛的[16]。 实际生产中,企业为了减少产品数据冗余,现有产品结构之间不能相互组合而成,因此组成库矩阵S的各列βi线性无关,这满足非负矩阵分解中原有矩阵各列向量线性无关的条件,因此该方法可以用来解决前文所述的产品结构相似性判断问题。 对应问题的描述为求解矩阵P=[pij]m2×r和Q=[qij]r×(n+1),使得S=PQ,基于MU算法,产品结构的非负矩阵分解及其相似性判定流程如图2所示,图中,I表示迭代总次数,不同的问题中,使‖S-PQ‖F在迭代过程中达到稳定所需的次数不尽相同,因此I的选取需要依据具体问题而定。因为该算法的分解结果与P、Q初始值的选取有关,因此,在实际计算过程中,一般重复多次计算矩阵分解过程,从中选取使‖S-PQ‖F最小的分解作为最终结果。 图2 相似性判定算法流程 为了验证非负矩阵分解方法的适用性,本文以文献[12]中某系列电灯的结构数据(图3~图11)为对象,表1说明了编码对应的产品零部件名称。图3~图11中连线旁边的数字表示生产一个父件所需要的子件数量。客户定制产品结构为S1,而D1~D8是企业现有产品的实例结构。企业设计人员需要从查询产品结构(企业现有产品结构)找出与目标产品结构(客户定制产品结构S1)最相似的产品结构,通过重用降低定制产品生产成本,缩短交货期。 图3 定制产品结构S1 图4 现有产品结构D1 图6 现有产品结构D3 图7 现有产品结构D4 图8 现有产品结构D5 图9 现有产品结构D6 图10 现有产品结构D7 图11 现有产品结构D8 编码名称编码名称B1007″基础部件B1018″基础部件S10014″黑色灯罩S10115″白色灯罩S10215″乳白色灯罩A100单孔电源部件A101三孔电源部件1100轴端12007″直径钢板12018″直径钢板1300毂14001/420螺丝1500持钎器1600单孔接口1601三孔接口1700连线部件21003/8″钢管220016表灯线2300标准插头引出端 以目标产品结构S1为例,按照如表2所示的零部件排列顺序,构建邻接矩阵Zs=[zij]20×20,根据图3所示的S1产品零部件关系以及权重,可知单个部件B100需要4个子零件1400。因为表2中部件B100的顺序为2,零件1400的顺序为13,所以Zs中元素z2(13)=4。依此表示方法类推可知,z12=z14=z17=z29=z2(10)=z2(12)=z7(14)=z7(15)=z7(17)=1,z9(18)=26,Zs中的其余元素均为零。 表2 零部件排列顺序 其他产品结构的邻接矩阵构建方法与此类似,不再赘述。接着按照前文所述,便可得到库矩阵S400×9。令r=3,于是库矩阵S400×9被分解为P400×3Q3×9的形式。在MATLAB软件中对算法编程实现,计算得矩阵Q: 矩阵Q中各列表示降维后各产品结构在三维空间中的坐标,其中,第1列表示目标产品结构,其余各列分别表示查询产品结构。分别计算矩阵Q中第1列即[0.11740.00320.1264]T,与第2列至第9列的欧氏距离,即目标产品结构与查询产品结构的相似性,列向量之间的距离越小表示对应的产品结构之间越相似,结果如表3所示。 表3 目标产品结构与查询产品结构之间的相似性结果 从表3中可以看出,查询产品结构S1与目标产品结构D1最相似,D6、D8则最不相似,该结果与文献[12]的方法计算结果相同。定制企业将会把产品结构D1及其零部件相关信息调出,实施资源重用,以减少定制企业在设计、管理等方面的工作。 非负矩阵分解方法主要是通过降维来实现快速相似性计算,因此具体降维的维度对于产品结构的相似性计算具有重要的影响。为此,在计算r分别为1、2、4、5时相似性计算结果、矩阵分解所引起的差异E=‖S-PQ‖F以及算法运行时间,并与前文(r=3)的结果作比较,如表4所示。 表4 r=1,2,3,4,5时相似性计算结果及程序运行时间 注:η为产品结构相似度。 从表4中可以发现,在计算产品结构之间的相似性时,为了找出最相似的查询产品结构,所选取的r不能过小。因为r过小会导致E偏大,即分解后的矩阵并不能完整描述原有产品结构,例如r=1,2时的计算结果差异较大,无法判断出最相似的结构产品。r较大时,需要更多的迭代计算步骤和时间,如表4最后一行所示。因此,在满足工程需求的情况下,企业可以根据生产和经营目标,选取合适的r作为相似性计算的降维目标。 同时,从表3中可以看出,文献[12]虽然采用了两种相似性度量方式,却无法判断出D1、D3、D4与目标产品S1相似度的差异,通过观察可以发现,事实上D1较D3、D4更相似于S1。本文提出的方法在确保D1、D3和D4相对于其他产品与S1更相似的基础上,对这三者的相似度进行了区分:D1最相似,D4次之,使结果更为合理。 此外,与文献[12]相比,本文提出的方法不但计算过程简化、结果更为合理,而且相似性计算结果具有更广的应用范围,由于上述矩阵Q包含了所有产品结构降维后在三维空间中的坐标,如表5所示。 表5 产品结构降维后在三维空间的坐标 上述三维坐标可以直观地反映在三维空间图中,于是,产品设计人员通过分析三维空间图中各点之间距离的远近,不仅能够直观、有效地发现与目标产品结构最相似的查询产品结构,以实现实例库产品结构重用,而且可以发现各查询产品结构之间的相似性程度,为实现相似产品结构实例融合、减少实例库冗余作准备。文献[12]提出的方法则只能够用于判断目标产品结构与各个查询产品结构之间的相似程度,不能同时发现查询产品结构之间的相似性关系,因此其应用范围具有局限性。 (1)给出了基于非负矩阵分解的产品结构相似性计算的思路及其数学描述。 (2)通过非负矩阵分解,实现了产品结构降维,简化了计算过程。 (3)本文提出的相似性计算方法不但计算比现有方法更加简单,而且产品结构之间的相似度更加容易区分,还便于设计人员发现查询产品结构之间的相似性。 [1]ElMaraghyH,SchuhG,ElMaraghyW,etal.ProductVarietyManagement[J].CIRPAnnals-ManufacturingTechnology,2013,62(2):629-652. [2]BhattaSR,GoelAK.FromDesignExperiencetoGenericMechanisms:Mode-basedLearninginAnalogicalDesign[J].ArtificialIntelligenceforEngineeringDesignAnalysisandManufacturing,1996,10(2):131-136. [3]贡智兵,李东波,于敏健.基于产品功能树的实例推理研究[J].中国机械工程,2006,17(2):123-126. GongZhibing,LiDongbo,YuMingjian.Case-basedReasoningBasedonProductFunctionalTree[J].ChinaMechanicalEngineering,2006,17(2):123-126. [4]TuzikovAV,RoerdinkJB,HeijmansHJ.SimilarityMeasuresforConvexPolyhedralBasedonMinkowskiAddition[J].PatternRecognition,2000,33(6):979-995. [5]OsadaR,FunkhouserT,ChazelleB,etal.Matching3DModelswithShapeDistributions[C]//InstituteofElectricalandElectronicsEngineers.2001InternationalConferenceonShapeModelingandApplications,ShapeModelingInternational(SMI).NewYork:IEEE,2001:154-166. [6]SunTL,SuCJ,MayerRJ,etal.ShapeSimilarityAssessmentofMechanicalPartsBasedonSolidModels[C]//DesignforManufacturingConference.SymposiumonComputerIntegratedConcurrentDesign.NewYork:ASME,1995:953-962. [7]SungR,ReaHJ,CorneyJR,etal.AssessingtheEffectivenessofFiltersforShapeMatching[C]//AmericanSocietyofMechanicalEngineers.2002InternationalMechanicalEngineeringCongressandExposition.NewYork:ASME,2002:687-696. [8]谌炎辉,周德俭,冯志君,等.基于BOM的复杂产品模块划分方法研究[J].中国机械工程,2012,23(21):2590-2593. ChenYanhui,ZhouDejian,FengZhijun,etal.ResearchonModularityMethodofComplexProductsBasedonBOM[J].ChinaMechanicalEngineering,2012,23(21):2590-2593. [9]丘宏俊,俞文静.产品结构相似度量方法[J].计算机工程,2010,36(9):274-27. QiuHongjun,YuWenjing.MethodforProductStructureSimilarityMeasurement[J].ComputerEngineering,2010,36(9):274-276. [10]RomanowskiCJ,NagiR.OnComparingBillsofMaterials:aSimilarity/DistanceMeasureforUnorderedTrees[J].IEEETransactionsonSystemsManandCyberneticsPartA:SystemsandHumans,2005,35(2):249-260. [11]TsaiCY,TienFC,PanTY.DevelopmentofanXML-basedStructuralProductRetrievalSystemforVirtualEnterprises[J].InternationalJournalofProductResearch,2004,42(8):1505-1524. [12]ShihHM.ProductStructure(BOM)-basedProductSimilarityMeasuresUsingOrthogonalProcrustesApproach[J].Computers&IndustrialEngineering,2011,61(3):608-628. [13]李乐,章毓晋.非负矩阵分解算法综述[J].电子学报,2008,36(4):737-743. LiLe,ZhangYujin.ASurveyonAlgorithmsforNon-negativeMatrixFactorization[J].ActaElectronicaSinica,2008,36(4):737-743. [14]PaateroP,TapperU.PositiveMatrixFactorization:aNon-negativeFactorModelwithOptimalUtilizationofErrorEstimatesofDataValues[J].Environmetrics,1994,5(2):111-126. [15]LeeDD,SeungHS.LearningthePartsofObjectsbyNon-negativeMatrixFactorization[J].Nature,1999,401(6755):788-791. [16]LeeDD,SeungHS.AlgorithmsforNon-negativeMatrixFactorization[C]//AdvancesinNeuralInformationProcessingSystems.Vancouver:NIPS,2001:556-562. (编辑张洋) Similarity Judgment of Product Structure Based on Non-negative Matrix Factorization and Its Applications Xu XinshengWang ChengXiao Ying China Jiliang University,Hangzhou,310018 In order to find reusable product structure promptly, an approach of measuring the similarity among product structures was proposed based on non-negative matrix factorization. A comprehensive matrix which containsed all structures was constructed on the basic of adjacent vectors that were transformed from the adjacent matrices of product structures. The non-negative matrix factorization for the comprehensive matrix was implemented based on Multiplicative Updates(MU) algorithm. Then all product structures might be described in low dimensional space. On the basis of these, the similarity between two product structures could be measured by calculating the Euclidean distance among these low dimensional vectors. Finally, an example was presented to verify the principles and methods mentioned above. The results show that the proposed methodologies are more effective than those of the existing methods. product structure;non-negative matrix factorization;similarity;Euclidean distance 徐新胜,男,1976年生。中国计量学院质量与安全工程学院副教授。主要研究方向为先进制造技术、大规模定制、产品质量管理。发表论文50余篇。王诚,男,1991年生。中国计量学院质量与安全工程学院硕士研究生。肖颖,女,1976年生。中国计量学院质量与安全工程学院讲师。 2015-06-18 国家自然科学基金资助项目(51405462,51175486);浙江省科技厅公益性技术应用研究计划资助项目(2013C31132,2014C31117) TP14; TH128 10.3969/j.issn.1004-132X.2016.08.014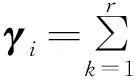


2 产品结构相似性判定的应用
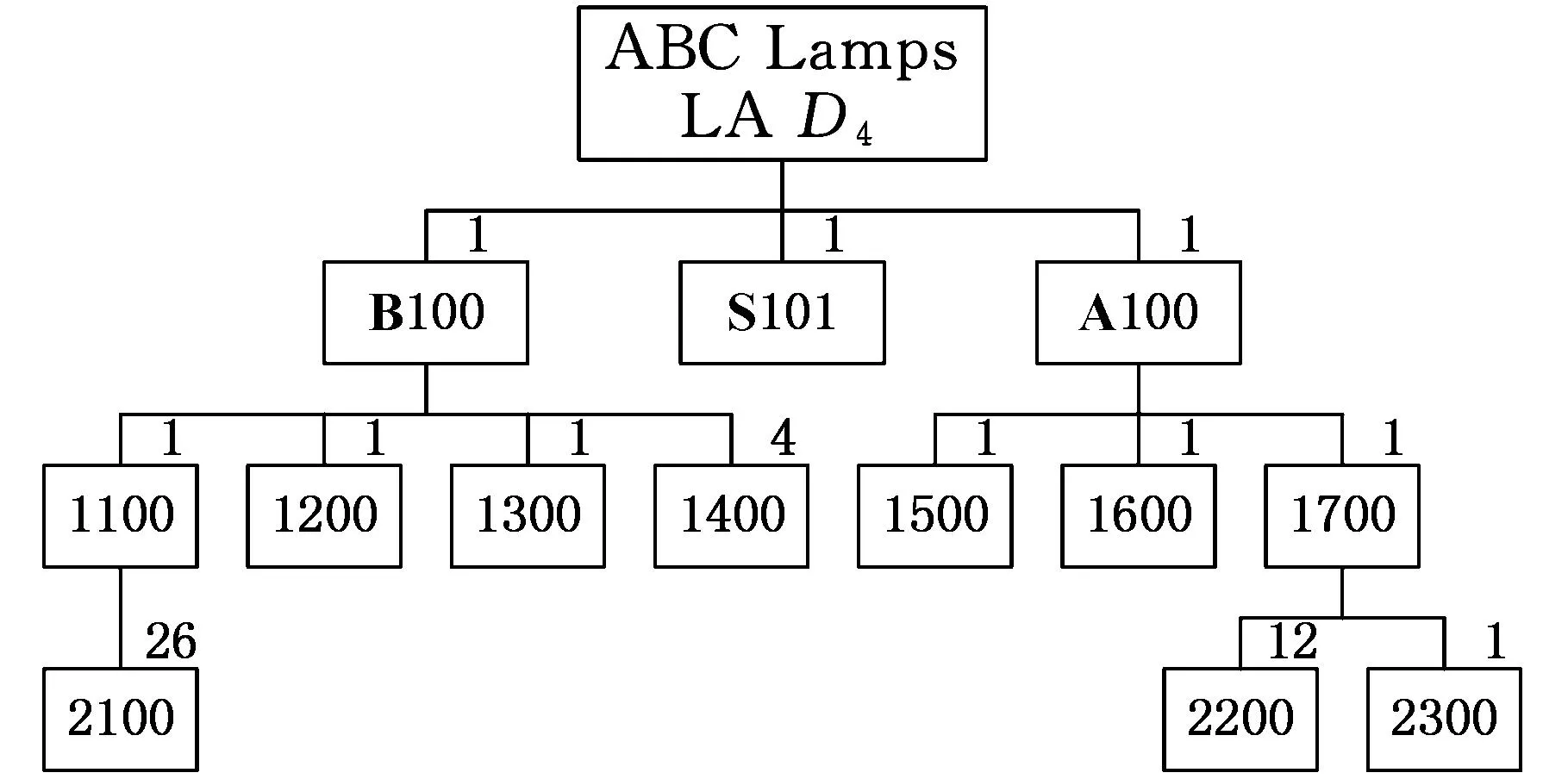
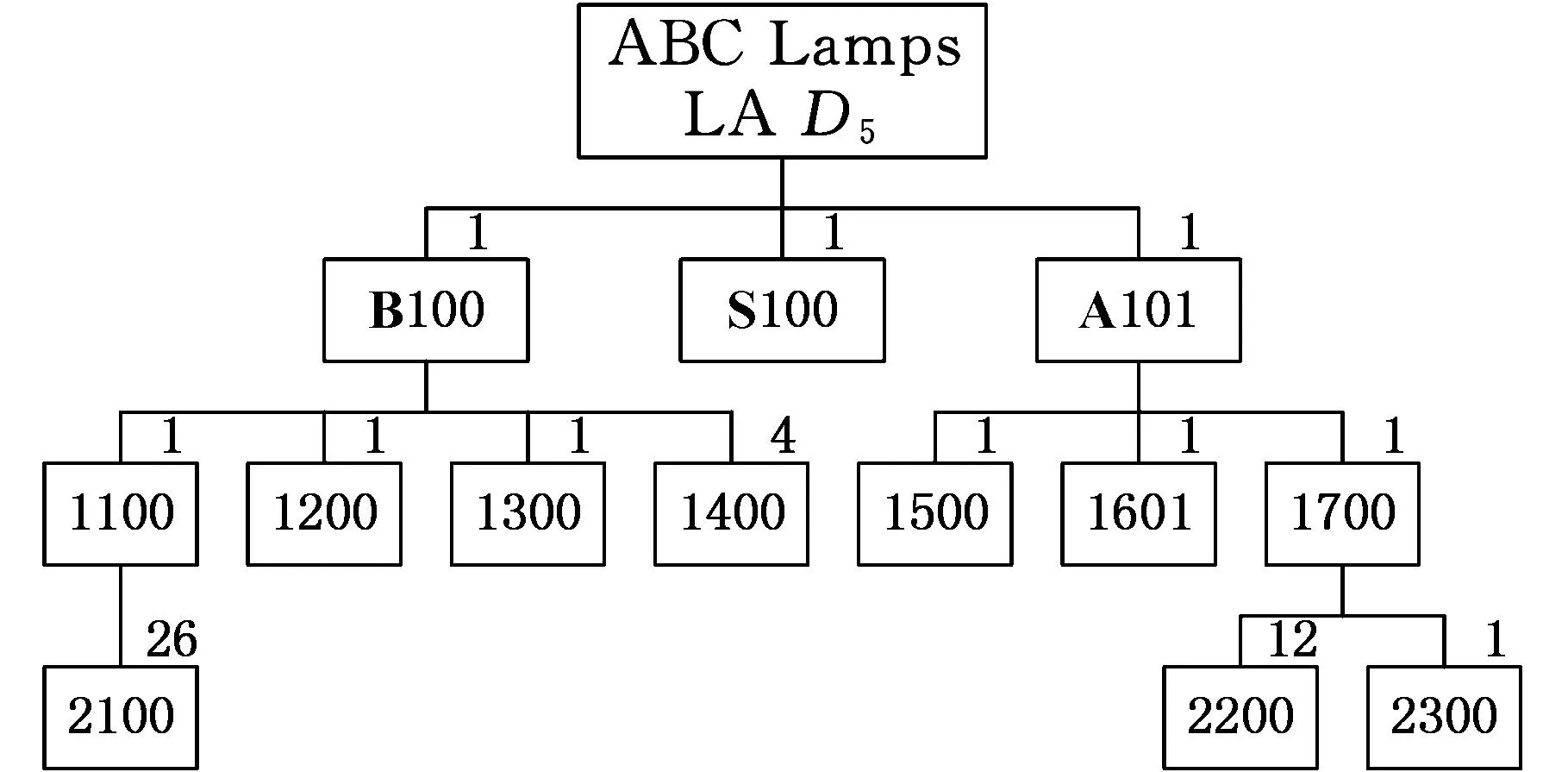


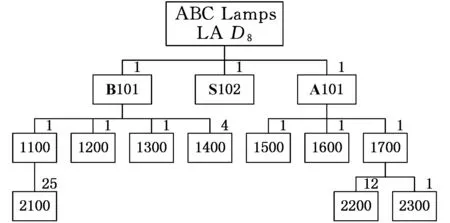


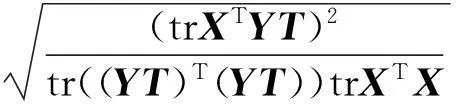
3 算法分析与管理内涵

4 结论
