导电聚合物驱动器电化学机械特性的研究
2016-08-16田素坤王湘江
田素坤 王湘江
南华大学,衡阳,421001
导电聚合物驱动器电化学机械特性的研究
田素坤王湘江
南华大学,衡阳,421001
采用自行搭建的导电聚合物驱动器弯曲特性测试实验系统,研究其电化学机械特性。对不同长度的驱动器施加0~1 V低电压,测量其顶端弯曲变形量;通过分析驱动器弯曲位移与电压的关系及位移与频率的关系,建立电机械转换模型。实验测试结果表明,电压与驱动器顶端力成线性关系;当电压为0.8 V、采样周期为0.02 s时,随着频率的增大,驱动器的弯曲位移逐渐减小。最后通过不同尺寸驱动器举起重物,验证了驱动器宽度越大,顶端弯曲力越大;驱动器长度越长,顶端弯曲力越小。
导电聚合物;聚吡咯;电机械转换模型;驱动器
0 引言
导电聚合物是由电性能和力学性能复合产生的一类极具发展潜力的功能复合材料。导电聚合物因具有能耗小、质轻、驱动电压小、生物相容性高、柔韧性好等优异特性,在仿生机器人和生物医学设备中具有广泛的应用前景,甚至在某些性能方面,导电聚合物与自然肌肉极为相似,被称为“人工肌肉”[1-4]。聚吡咯(PPy)、聚苯胺(PAN)、聚噻吩(PTh)是三种最常见的导电聚合物。导电聚合物巨大的发展潜力引起了许多学者的研究兴趣。李新贵等[5]将自然肌肉与人工肌肉进行对比,指出人工肌肉具有柔韧性好、能耗小、生物相容性高等优异的特性,是一种很有发展潜力的高分子材料。李永航[6]对聚吡咯、聚苯胺等导电聚合物的电化学性能及其反应机理进行了研究,并对其电化学稳定性进行讨论。Christophersen等[7]研究了不同尺寸的双层聚吡咯弯曲型驱动器的特性和建模。Gaihre等[8]制作出的微尺度三层弯曲型聚合物驱动器可用于细胞诊断、生物纳米系统、数据存储器等领域。Madden等[9]根据双层导电聚合物驱动器的工作原理,建立了等效电路图,并提出了离子扩散-机械弹性变形的数学模型。以上研究都只是针对导电聚合物的性能和实际应用,并没有建立驱动器的电机械转换模型。本文根据导电聚合物驱动器的工作原理,参考材料固有参数和驱动器尺寸,结合实验建立了驱动器的电机械转换模型,并且通过实验验证了驱动器顶端是否可以承受力。
1 驱动器驱动机理
图1为实验用三层弯曲型导电聚合物驱动器示意图。结构主要有三层:两个具有电活性的聚吡咯层和一个非导电多孔隙聚偏氟乙烯(PVDF)层。PPy层厚度约为30 μm,用于实现溶液中离子的交换,PVDF层厚度约为110 μm,用于储存电解液(Li+TFSI-)。PVDF层两侧通过离子溅射技术镀上很薄的多孔隙金层(离子可自由通过),厚度约为1~10 nm,作为两个电极使用,用来提高驱动器的导电性和刚度。

图1 导电聚合物驱动器示意图
驱动器PPy层两侧通入电压后,其内部将在形成的电场作用下发生氧化还原反应,其化学反应过程为
(1)氧化反应
PPy+TFSI-→PPy+TFSI-+e-
(2)还原反应
PPy+TFSI-+e-→PPy+TFSI-
参考化学反应过程和图2的离子迁移示意图,TFSI-作为PPy的掺杂离子,施加电压后,正极PPy层氧化膨胀,负极PPy层还原收缩。为使驱动器内部显电中性,电解质中的TFSI-向带正电荷的PPy层迁移,而膜内的阳离子由于固定在高分子链上,所以不发生迁移;同时,由于TFSI-离子亲水性较好,迁移过程中伴随着水合水分子的移动对体积改变也有一定影响[4,8,10],最终膜内水合水分子和阴离子聚集在阳极附近,膜内产生压力差使PPy层体积发生改变,进而导致驱动器顶端(自由端)向电源负极方向弯曲,即将内部的电化学能转为机械功,如图2b所示。
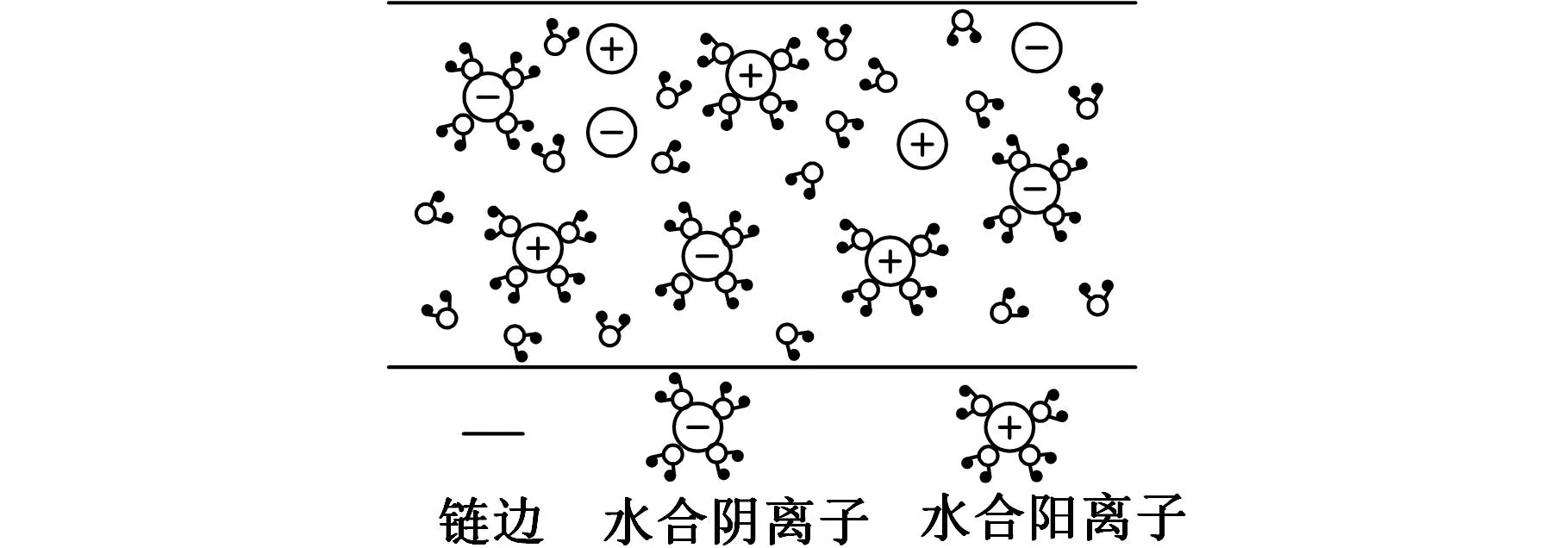
(a)施加电压前
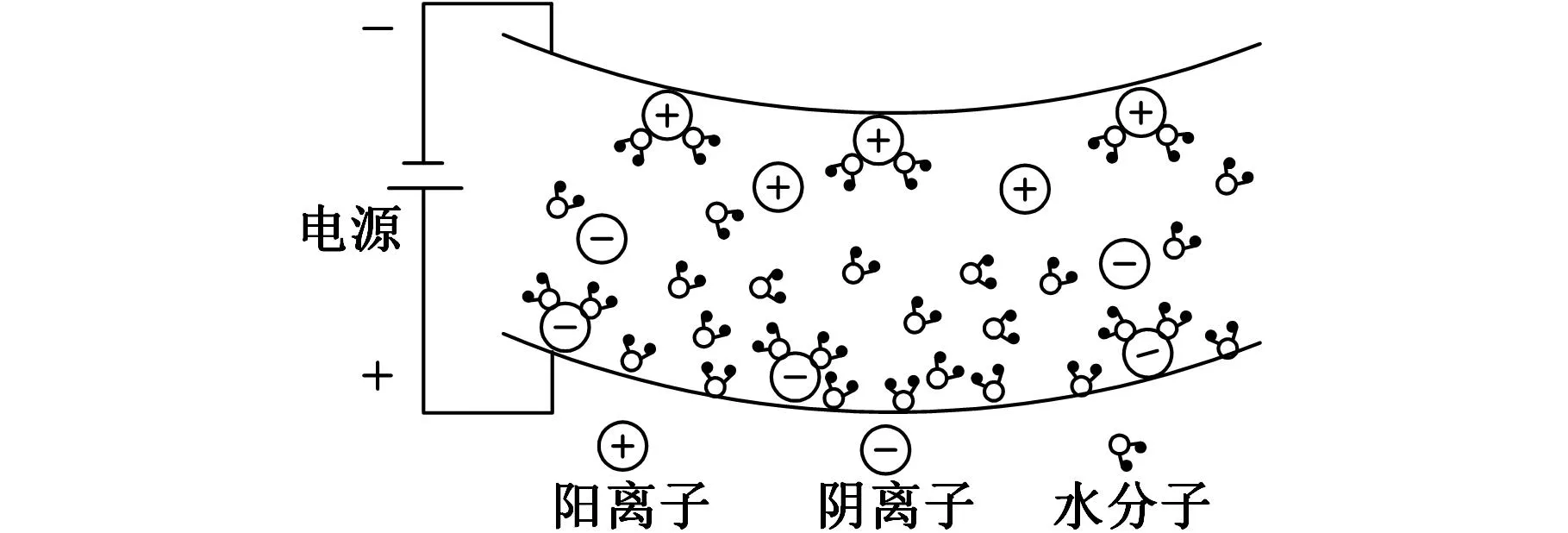
(b)施加电压后图2 离子迁移示意图
2 实验测试及结果
导电复合材料的电致伸缩效应主要表现在其自身的变形上,0~1 V低电压就可以让驱动器自由端发生大变形,其形变量相对其他智能材料比较大。即使电压很小时,其形变量也是存在的,只是肉眼很难观察到,此处使用激光位移传感器对驱动器在0~1 V低电压下的电响应进行测量,激光位移传感器最小分辨力为20 μm,模拟输出0~10 V电压信号,通过比例换算成位移值,经PCI数据采集卡传入计算机中。整个驱动器位移测试装置示意图见图3,主要采用数字函数信号发生器(F20A)、高速摄像机(InLine系列)、激光位移传感器(FT50)、PCI数据采集卡(PCI-1710U)以及电子天平(FA1104N)等设备进行数据的采集和测量,并进行分析计算。
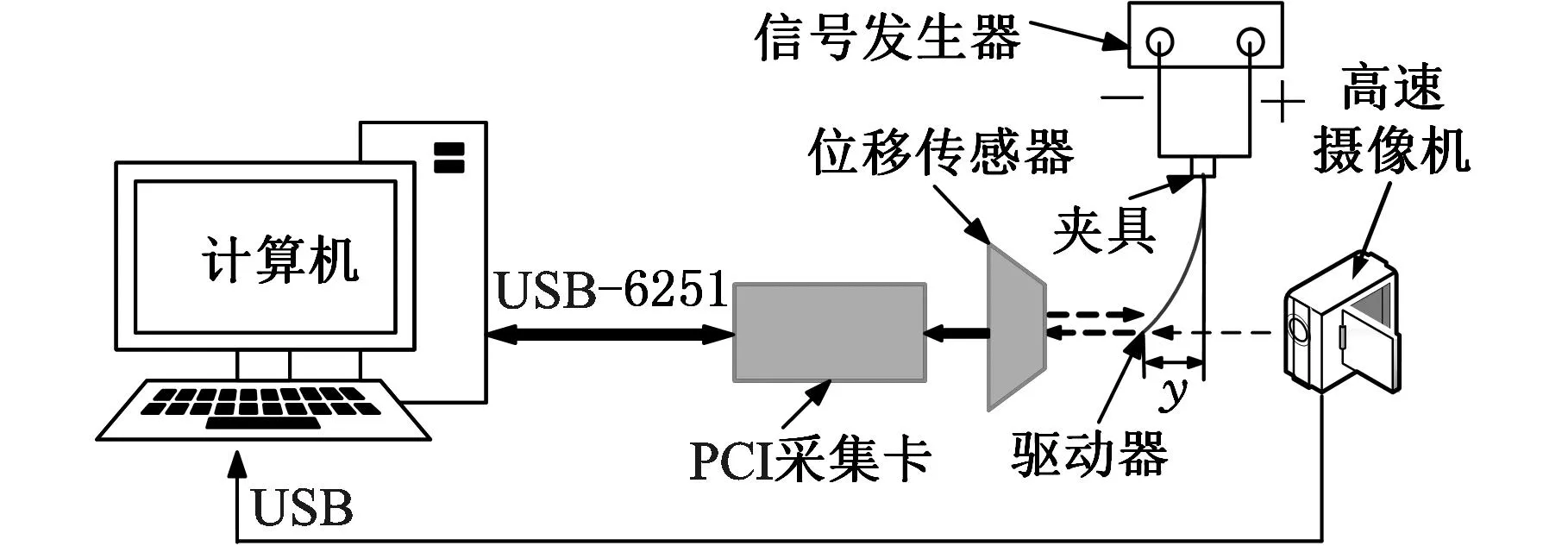
图3 驱动器位移测试系统示意图
文中选用含有0.5 mol双三氟甲基磺酰亚胺锂(Li+TFSI-)的碳酸丙烯酯溶剂溶液作为实验用电解液,而条形驱动器则是从大块样本中剪切得到,每次试验前需将其存储在此溶液中30 min直到使用。施加阶跃电压后,随着通电时间的延长,驱动器的运动过程如图4所示。当驱动器处于图4中a位置时,施加0.4 V的正向电压,驱动器自由端沿顺时针方向弯曲到图b位置,历时5 s,随着时间的延长,驱动器达到图c位置,最终稳定到图d位置。上述即为驱动器在0.4 V电压下的整个运动过程,达到稳定状态共需要15 s,最终恢复到初始位置。表1给出尺寸为6 mm×2 mm×0.17 mm的驱动器在0~1 V低电压下的偏转位移。

t=0 s t=5 s t=10 s t=15 s图4 驱动器运动过程图
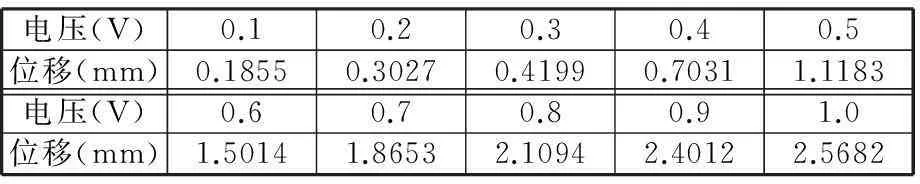
电压(V)0.10.20.30.40.5位移(mm)0.18550.30270.41990.70311.1183电压(V)0.60.70.80.91.0位移(mm)1.50141.86532.10942.40122.5682
在人工肌肉的实际应用中,通常需要对设计出的微操纵装置进行力学分析。本文依据导电聚合物驱动器的工作原理,参考材料固有参数和驱动器尺寸,鉴于其自身特性和广泛的应用前景,从驱动器的实际应用出发将其等效成悬臂梁结构[11],如图5所示。
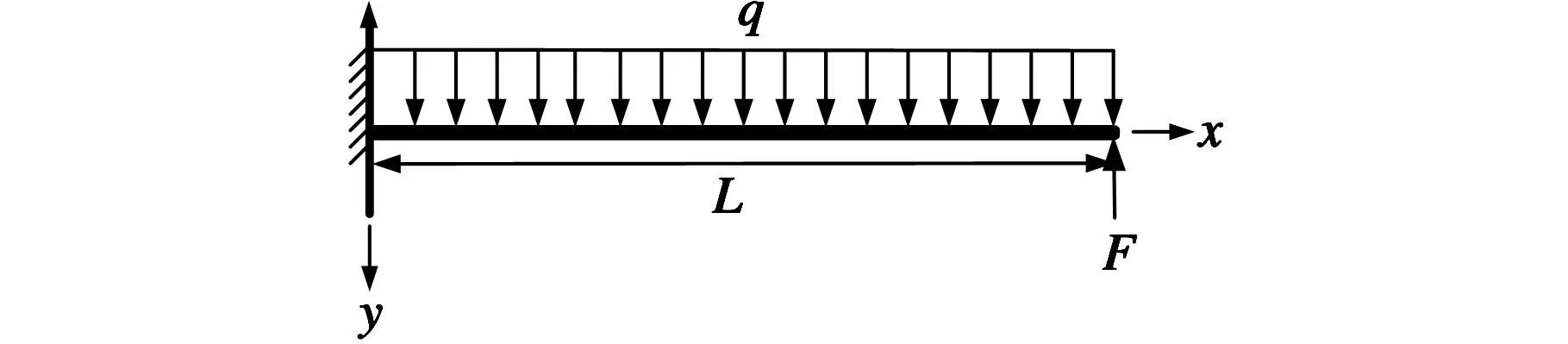
图5 驱动器悬臂梁模型
在小变形的前提下,给出悬臂梁的挠曲线方程如下:
(1)
式中,ωq为载荷q作用下驱动器的弯曲挠度;EI为刚度,EI=0.145 367N·mm2。
由式(1)计算出不同电压下的等效均布载荷值,如表2所示。

表2 驱动器稳定电压下的均布载荷值
参考图5,使用叠加法求变形,根据变形协调条件,可列出变形后的顶端力F:
(2)
通过式(2)得到的数据拟合出电压与顶端力的线性关系,如图6所示。拟合曲线的相关系数R2=0.9813,说明数据的拟合程度好,拟合可信度高。建立电压(单位V)与顶端力的函数关系式:
F=0.005 92U-5.9739×10-4(mN)
(3)
参照图5和驱动器的弯曲特性,可以推出等效均布载荷的方向与电压的正负极有关,并且等效均布载荷的方向与驱动器的实际位移方向一致。
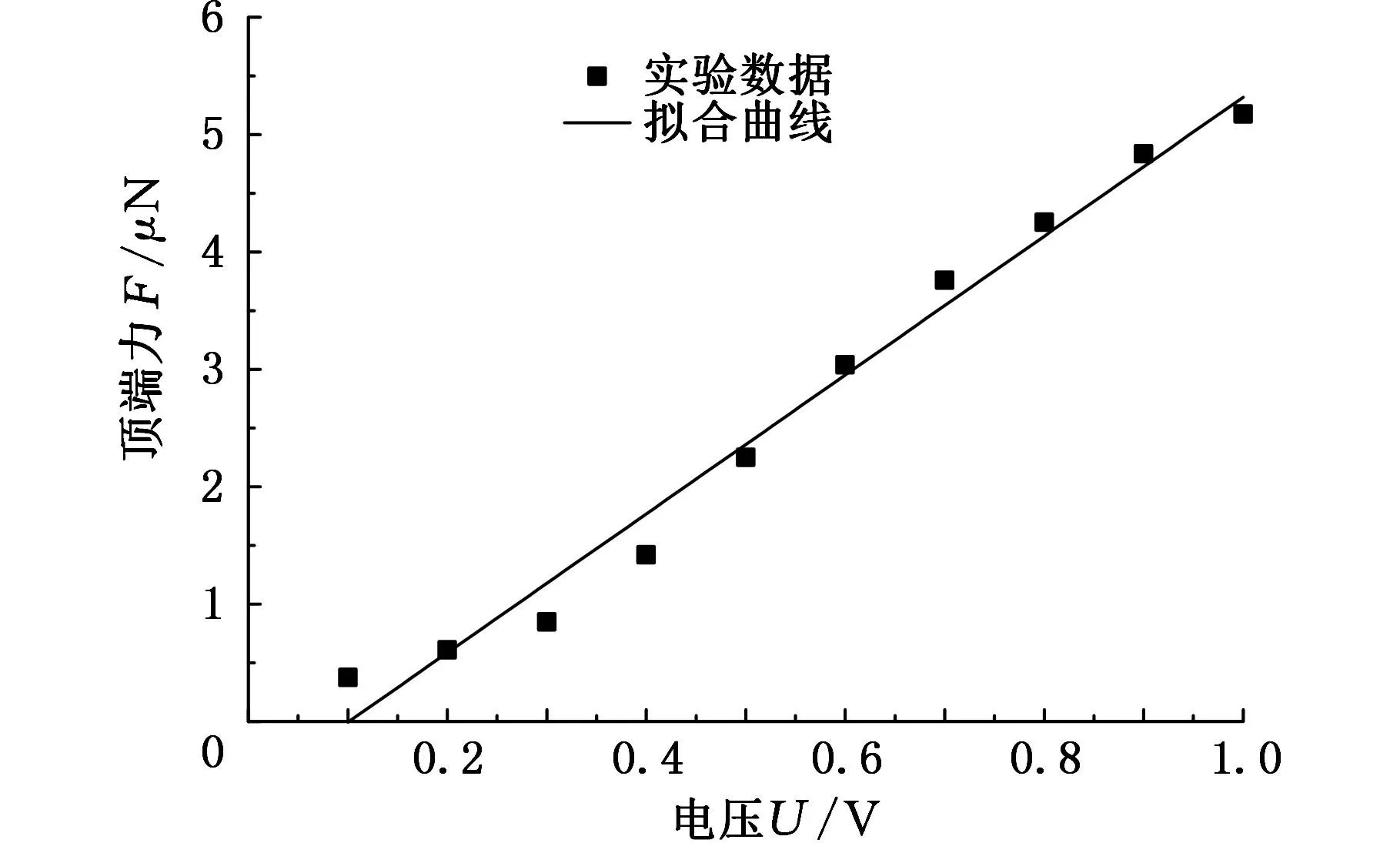
图6 电压与顶端力的关系
在0.8V电压下,采样周期设置为0.02s,对尺寸为6mm×2mm×0.17mm的驱动器施加不同频率的正弦电压,测得实验数据,拟合出如图7所示的曲线,相关系数R2=0.943 67,得出关系式:
s=0.360 49+2.083 25×0.0067f(mm)
(4)
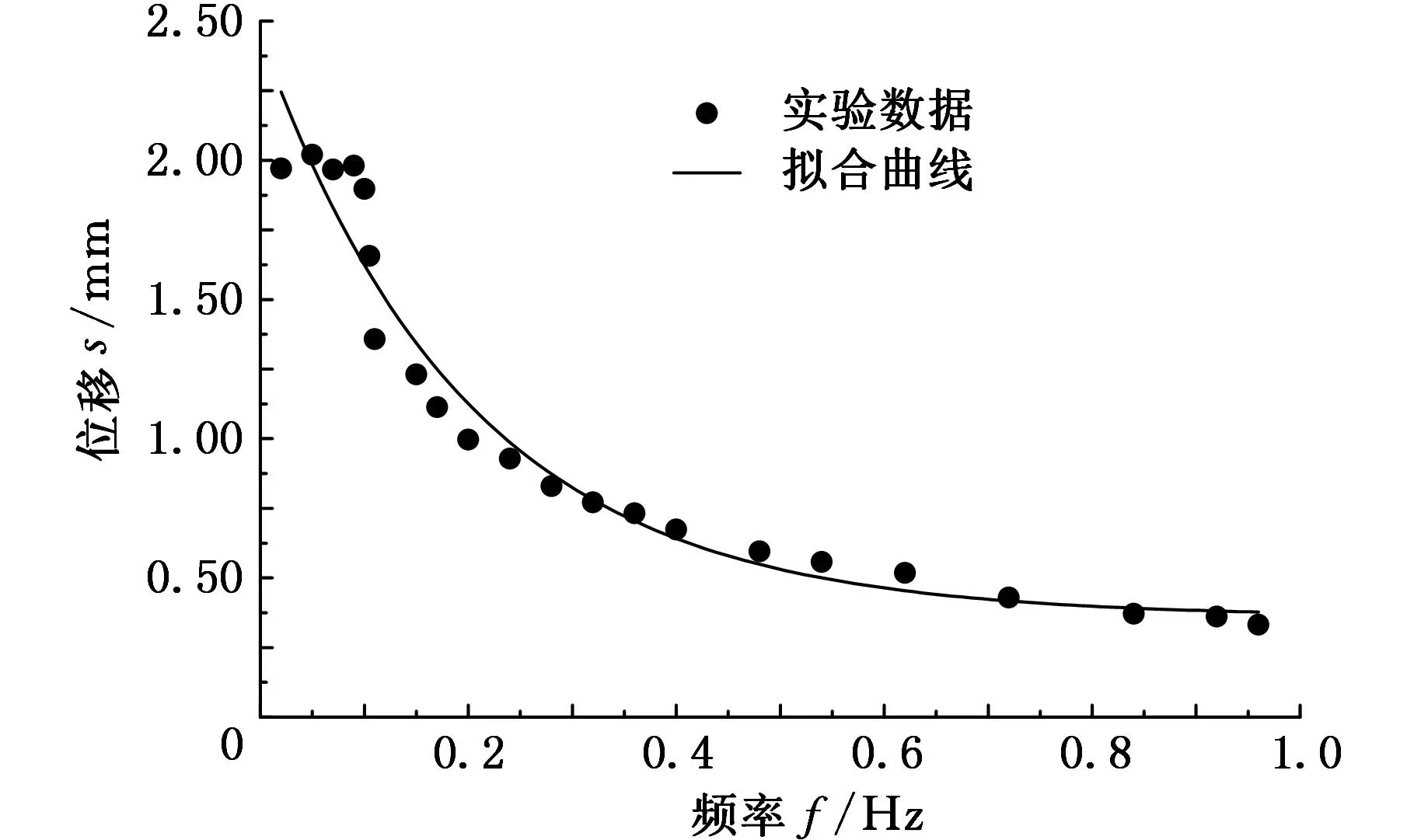
图7 频率与位移的关系
从图7中可以看出,当电压频率小于0.1Hz时,测得自由端偏转位移基本稳定,且位移值最大;频率在0.1~0.3Hz范围内,偏转位移大幅度下降;大于0.3Hz时,偏转位移变化缓慢。这说明在电压一定、频率小于0.1Hz时,导电聚合物驱动器可以达到该电压下的最大位移;而当频率大于0.1Hz时,因驱动器反应速度慢和反向电压的原因导致驱动器反向弯曲,并且没达到最大偏转位移。所以导电聚合物驱动器的电致伸缩特性具有频率低通性。
采用自由端弯曲位移完全吻合法,将式(4)代入式(1)中得出均布载荷与频率f的关系式:
q=3.234 77×10-4+0.001 87×0.0067f(MPa)
(5)
根据式(5)即可计算出不同频率下的均布载荷。式(3)和式(5)给出电压与力、频率与均布载荷的函数关系,从而完成了驱动器电机械转换模型的建立。将转换模型计算出的驱动器顶端位移值与实验测得值进行对比,结果如图8和图9所示,通过对比位移值来验证电机械转换模型的准确性。
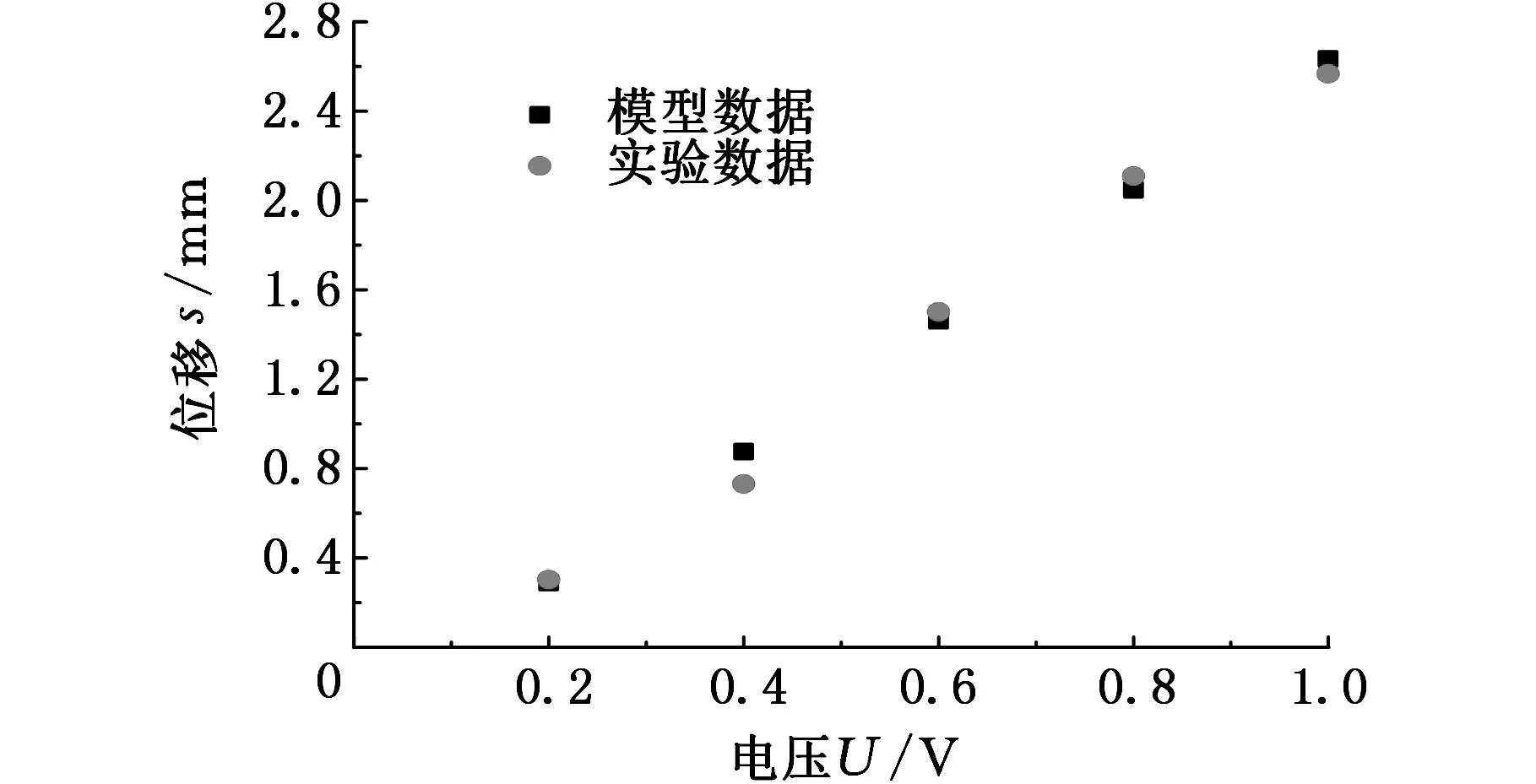
图8 电压转换模型计算值与实验对比
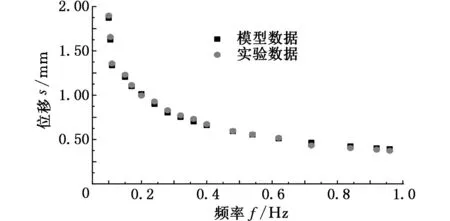
图9 频率转换模型计算值与实验对比
从图8和图9中可以看出,由转换模型得出的位移值与实测值吻合程度非常好,因此式(3)和式(5)作为电机械转换模型是非常合理的。
图10为测试驱动器顶端负载能力的测力结构示意图,通过驱动器举起重物来说明其顶端力的存在。采用电子天平称出单片条形驱动器(10mm×2mm×0.17mm)的重量为4.5mg,微型磁铁固定在距离驱动器顶端1mm处,磁铁直径为1mm,厚度为0.5mm,8片磁铁的总重量为21.2mg。参照图5,将驱动器顶端承受的力等价为微型磁铁的重力Fg,即F=Fg=mg,m为磁铁的质量。图11为高速摄像机拍摄到的驱动器弯曲运动图。通过实验测得,在有负载的情况下,施加1V电压时,对宽度为2mm、2.5mm、3mm、4mm的驱动器(长为10mm)进行受力测试,最终结论是(表3):驱动器宽度越大,位移越大,即顶端力越大。表4为2mm宽驱动器顶端位移与长度的关系,从表中可以看出,存在负载时,驱动器长度越长,位移越小,即顶端力越小。
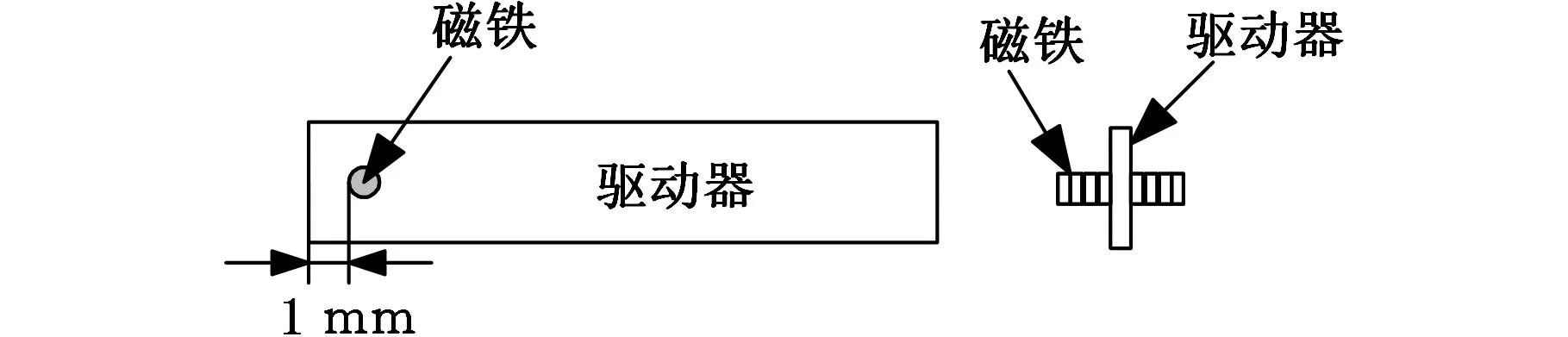
图10 驱动器顶端测力结构示意图

图11 驱动器弯曲运动实测图

驱动器宽度(mm)2.02.53.04.0驱动器位移(mm)3.88233.91033.97504.0963
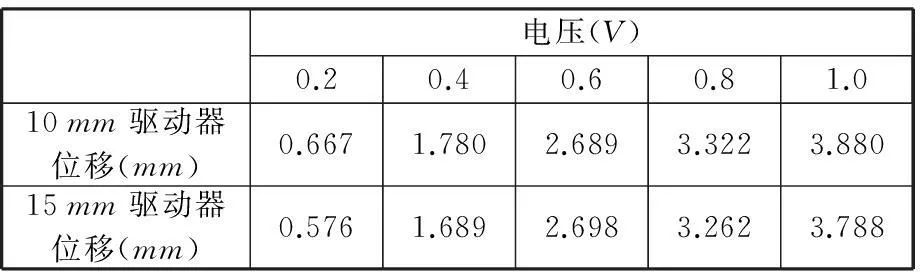
表4 不同长度驱动器的偏转位移
3 总结
(1)根据TFSI-离子在电场作用下迁移运动导致驱动器PPy层体积变化的机理,研究驱动器的弯曲运动。采用驱动材料为PPy的导电聚合物驱动器搭建实验系统,分别测量出不同电压和频率下驱动器的偏转位移。
(2)通过研究尺寸为6mm×2mm的驱动器弯曲位移与电压、位移与频率的关系,建立电压与顶端力的关系式:F=0.005 92U-5.9739×10-4(mN);当电压为0.8V、采样周期为0.02s时,建立频率与均布载荷的关系式:q=3.234 77×10-4+0.001 87×0.0067f(MPa)。
(3)通过驱动器顶端固定一定重量的磁铁,验证驱动器顶端可以承受力。且在施加1V电压时,驱动器宽度越宽,位移越大;驱动器长度越长,位移越小。
[1]Mutlu R, Alici G. Artificial Muscles with Adjustable Stiffness [J]. Smart Materials and Structures, 2010, 19(4): 45004-45013.
[2]Han Gaoyi, Shi Gaoquan. Conducting Polymer Electrochemical Actuator Made of High-strength Three-layered Composite Films of Polythiophene and Polypyrrole [J]. Sensors and Actuators B, 2004, 99: 525-531.
[3]Xiangjiang Wang, Alici G, Nguyen C H. Adaptive Sliding Mode Control of Tri-layer Conjugated Polymer Actuators [J]. Smart Materials and Structures, 2013, 22(2): 025004.
[4]Nguyen C H, Alici G, Wallace G G. Modelling Trilayer Conjugated Polymer Actuators for Their Sensorless Position Control [J]. Sensors and Actuators A, 2012,185(5):82-91.
[5]李新贵,张瑞锐,黄美容,等.导电聚合物人工肌肉[J].材料科学与工程学报,2004, 22(1): 128-131.
Li Xingui, Zhang Ruirui, Huang Meirong, et al. Artificial Muscles Based on Conducting Polymers[J]. Journal of Materials Science and Engineering, 2004, 22(1): 128-131.
[6]李永航.导电聚合物的电化学性质[J].复旦学报(自然科学版),2004, 43(4): 468-481.
Li Yonghang. Electrochemical Properties of Conducting Polymers [J]. Journal of Fudan University(Natural Science),2004, 43(4): 468-481.
[7]Christophersen M, Shapiro B, Smela E. Characterization and Modeling of PPy Bilayer Microactuators: Part 1. Curvature[J]. Sensors and Actuators B, Chemical, 2006, 115(2): 596-609.
[8]Gaihre B, Alici G, Geoffrey M. Spinks, et al. Synthesis and Performance Evaluation of Thin Film PPy-PVDF Multilayer Electroactive Polymer Actuators [J]. Sensors and Actuators A, 2011, 165: 321-328.
[9]Madden P G A, Madden J D W, Anquetil P A, et al. The Relation of Conducting Polymer Actuator Material Properties to Performance[J]. IEEE J. Ocean. Eng. , 2004, 29(3): 696-705.
[10]Fang Y, Tan X. B. A Novel Diaphragm Micropump Actuated by Conjugated Polymer Petals: Fabrication, Modeling, and Experimental Results[J]. Sensors and Actuators A: Physical. 2010, 158(1): 121-131.
[11]Alici G, Mui B, Cook C. Bending Modeling and Its Experimental Verification for Conducting Polymer Actuators Dedicated to Manipulation Applications[J]. Sensors and Actuators A: Physical, 2006, 12(6):396-404.
(编辑王旻玥)
Study on Electrochemical-mechanical Characteristics of Conductive Polymer Actuator
Tian SukunWang Xiangjiang
University of South China, Hengyang, Hunan, 421001
The bend characteristics testing experimental system was set up by actuator to study the electrochemical-mechanical characteristics. The bending deformation was measured by applying low voltage(0 ~ 1 V) to the actuator with different lengths. The relationship among the bending displacement, the voltage and the voltage frequency was analyzed. The electric-mechanical transfer model was established based on the experimental results. The results show that the voltage and the bending force are in a linear relationship. When the voltage is 0.8 V and sampling period is 0.02 s, the bending displacement of the actuator decreases gradually with the increase of the frequency. Furthermore, it is verified by lifting the weights of the drive of different sizes,the larger the width of the drive, the larger the bending force, and the longer the length, the smaller the bending force.
conductive polymer; polypyrrole; electric-mechanical transfer model; actuator
田素坤,男,1989年生。南华大学机械工程学院硕士研究生。研究方向为智能材料驱动控制和机电系统控制。王湘江,男,1972年生。南华大学机械工程学院教授。
2015-05-08
湖南省教育厅重点资助项目(13A081)
TP212
10.3969/j.issn.1004-132X.2016.08.009
