刍议如何提高线性代数课程的教学效果

2016-08-15赵婷

赤峰学院学报·自然科学版 2016年13期

关键词：行列式线性方程组特征向量

赵婷

（河南科技学院　数学科学学院，河南　新乡　453003）

刍议如何提高线性代数课程的教学效果

赵婷

（河南科技学院数学科学学院，河南新乡453003）

通过《线性代数》课程现状分析，根据近几年的教学经验，提出从五个方面更好地提高线性代数课堂教学效果，即培养学生的学习兴趣，以解线性方程组为主线，采用问题式教学法，将理论与实际相结合，增加实验教学.

线性代数；问题式教学；MATLB；线性相关

《线性代数》作为高等院校一门重要的基础数学课程，在自然科学、现代工程技术、管理科学、统计学、信息安全等诸多领域有着广泛的应用，它不仅是学习后续课程不可缺少的工具，而且能够培养学生的抽象思维能力、科学运算能力、综合分析解决问题的能力.但由于《线性代数》概念定理的高度抽象性，学时的限制，大班授课等因素影响，很多学生觉得《线性代数》难学和不易掌握.随着科技的发展以及近年来高校的不断扩招，提高线性代数课堂教学效果显得尤为重要.根据笔者实际教学经验和总结，提高《线性代数》课堂教学效果应从以下五个方面做起.

1　培养学生的学习兴趣

从中学进入大学后，大部分学生脱离了教师的严格要求，无法顺利进入几乎完全靠自觉的学习阶段.由于《线性代数》课程其逻辑性高、抽象性强、难度大的特点，相当一部分学生在学习过程中信心不足，更有一部分学生被动学习，本着“考前突击两周，60分万岁”的态度应付考试.作为教师要学会激发学生的学习兴趣.首先，在教学过程中，根据教学内容，由简到难、循序渐进地引导学生学习思考；其次，合理设置教学目标，并将这些目标分成小的子目标，当学生完成一个小目标时，及时给予肯定，表扬；另外，设计有趣的课堂引入，激发学生的好奇心，将理论与实际应用相结合，将抽象的数学概念具体形象化.此外，应用情感因素，与学生建立平等友好的师生关系［1］，尊重学生，以友善、平等、宽容的态度对待学生，成为学生的朋友.

2　以解线性方程组为主线

《线性代数》包含行列式、矩阵、向量的线性相关性、线性方程组、相似矩阵及二次型、线性空间与线性变换这几部分.每一部分，仿佛是一个孤立的小山，登上一个并不能顺利地通向另一个［2］.其实这些分块内容都是围绕着解线性方程组.由解特殊线性方程组即未知数个数与方程个数相等且方程中没有多余的方程引出了行列式的概念，接着研究行列式的定义、性质，最后提出用克莱姆法则解决此类线性方程组的求解问题；对于一般的线性方程组怎么来求解，引出了矩阵的概念，矩阵与线性方程组是一一对应关系，因此研究一般线性方程的求解问题就转化成矩阵问题，通过矩阵的初等行变换来求解线性方程组.但是，矩阵理论并没有说清楚线性方程组的解与解之间的关系.于是，引入了向量概念，向量组与矩阵是一一对应关系，从而向量组与线性方程组也是一一对应关系，从向量的线性相关性得到了齐次线性方程组的基础解系，通过基础解系得到了齐次线性方程组的解的结构，进而得到非齐次线性方程组解的结构.到此关于线性方程组的求解问题得到了完满地解决.二次型是对于线性方程组解法的综合应用，其中涉及了矩阵的特征值特征向量.所以，以线性方程组为主线，有助于学生从整体理解线性代数的内容，把零散、孤立的知识成串，而且符合学生的认知结构，学生更容易接受.

3　采用问题式教学法

巴西著名学者保罗·弗莱雷指出，“以教师为中心”的课堂教学方式是将“人”变成“物”和“器”的教学方式，本质上是典型的“储蓄式教育”.因为它把学生变成了任由教师灌输的“存储器”.在传统的讲授式课堂教学中，教师往往只需要把课前准备好的教学内容通过口头讲授方式传递给学生即可，课堂上好学生安静被动地听、抄、存储知识；一些不认真学习的学生则上网、玩手机、睡觉或者低声交谈.整个教学过程中，很少有学生主动与教师互动交流.认知心理学发现，“学习是一个主动的建构过程”，一般学生都会“通过关联自己已有的知识和经验去理解新的概念，而不是简单地把他们所读所听的东西原样反射到大脑中”［3］.《线性代数》中一些重要概念、定理的引出上，应该改变传统的教学方式，采用问题式教学法［4］，启发学生深入思考，主动与已有知识联系起来，让学生在课程学习过程中主动建构.这样，新的知识才能更容易的被接受、消化.

向量组的线性表示中，一个向量b能由一个向量组a1，a2，…，am线性表示，是指存在一组实数k1，k2，…，km使得k1a1+k2a2+…+kmam=b，否则，称b不能由一个向量组a1，a2，…，am线性表示.那么给出具体的向量b能由一个向量组a1，a2，…，am，我们怎么判断能不能线性表示呢？

一个向量b能由一个向量组a1，a2，…，am线性表示

⇔存在一组实数k1，k2，…，km，使得

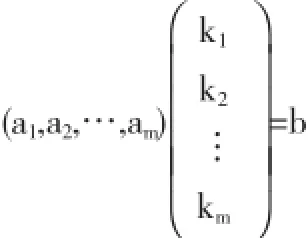
⇔设A=（a1，a2，…，am），存在k=（k1，k2，…，km）T，有Ak=b

⇔k=（k1，k2，…，km）T是方程Ax=b的解

⇔方程Ax=b有解

⇔R（A）=R（A，b）

向量组的线性相关中，一个向量组a1，a2，…，am线性相关，是指存在一组不全为零的实数k1，k2，…，km使得k1a1+k2a2+ …+kmam=0，否则，称向量组a1，a2，…，am线性无关.那么给出具体的一个向量组a1，a2，…，am，我们怎么判断能不能它的线性相关性呢？

一个向量组a1，a2，…，am线性相关

⇔存在一组不全为零的实数k1，k2，…，km，使得k1a1+k2a2+ …+kmam=0

⇔存在一组不全为零的实数k1，k2，…，km，使得

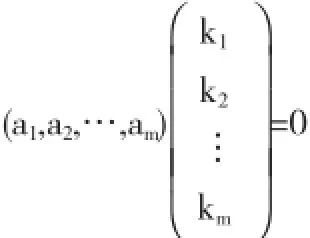
⇔设A=（a1，a2，…，am），存在k=（k1，k2，…，km）T≠0，有Ak=0

⇔k=（k1，k2，…，km）T≠0是方程Ax=0的解

⇔方程Ax=0有非零解

⇔R（A）＜m

一个向量组a1，a2，…，am线性无关

⇔只有实数k1，k2，…，km全为零时，才能使得k1a1+k2a2+…+kmam=0

⇔只有实数k1，k2，…，km全为零时，才能使得

⇔设A=（a1，a2，…，am），只有k=（k1，k2，…，km）T=0，才有Ak=0

⇔方程Ax=0只有零解

⇔R（A）=m

方阵A的特征值特征向量是指，一个n维非零向量p，使得Ap=λp，其中λ是一个实数，则数λ称为A的特征值，非零向量p称为A的对应特征值λ的特征向量.如果已知n阶方阵A，我们怎么来找到它的特征值和特征向量呢？

数λ是n阶方阵A的特征值

⇒存在一个非零向量p，使得Ap=λp

⇒存在一个非零向量p，使得（A-λE）p=0

⇒p是方程（A-λE）x=0非零解

⇒方程（A-λE）x=0有非零解

⇒|A-λE|=0

那所有满足|A-λE|=0的数λ是不是都是A的特征值呢？

数λ满足|A-λE|=0

⇒方程（A-λE）x=-有非零解

⇒任取方程（A-λE）x=0的一个非零解p

⇒（A-λE）p=0，p≠0

⇒Ap=λp，p≠0

⇒数λ是A的特征值，非零向量p为特征值λ的特征向量

通过上面的问题分析，我们可以得到，数λ是A的特征值⇔|A-λE|=0，而λ的特征向量是方程（A-λE）=0的非零解，而方程（A-λE）x=0的任一非零解都是特征值λ的特征向量，故λ的所有特征向量就是方程（A-λE）x=0的全部非零解.

向量组的线性表示、线性相关性以及求方阵的特征值特征向量的判断及求解本质还是归结到线性方程组解的问题，这也说明了《线性代数》以“解线性方程组”为主线的观点.我们采用问题式教学法学习向量组的线性表示、线性相关性以及方阵的特征值特征向量，即弄清楚了怎么判断一个向量能否由一个向量组线性表示，向量组线性相关与否以及方阵特征值特征向量的求法，而且与已掌握的解线性方程组的知识结构联系起来，学生能更好的消化、吸收.

4　联系实际生动形象讲解

对于抽象、严密、系统的数学课，如果教师不注意讲课语言、授课方式，学生往往觉得数学课枯燥乏味、犹如听“天书”一样.因此，教师应结合线性代数教学内容，尽量从生活的实际例子出发，把复杂、难懂、不好理解的知识变得形象、具体.通过加入调味品，课堂气氛轻松、活跃，而且提高了学生的学习兴趣.

设方阵A，当A的行列式不等于0时，A为可逆矩阵；当A的行列式等于0时，A为不可逆矩阵.这些是我们熟知的，但当A的行列式不等于0时，A又称为非奇异矩阵；当A的行列式等于0时，称为奇异矩阵.学生普遍反映对奇异非奇异矩阵记不住，不能快速判断行列式不等于0时，到底是奇异矩阵还是非奇异矩阵.对于这个定义我们可以联想记忆，水果中猕猴桃又叫奇异果，它的形状像数字“0”，因此，A的行列式等于0时，即“等于奇异果”时，A为奇异矩阵；A的行列式不等于0时，即“不等于奇异果”时，A为非奇异矩阵.

在给定矩阵A，求A的行最简形矩阵F，并求可逆矩阵P，使得PA=F.常采用的方法是利用初等行变换把矩阵（A，E）化成（F，P）.但是学生对这种方法理解起来很吃力.可以这样讲解，把单位矩阵E比喻成A身上绑的“计步器”［5］.E可以记录A每一步，当A变换成行最简形F时，“计步器”E就变成所求的可逆矩阵P.

向量组的线性组合以及线性表示，可以用生活中的1，2，5，10元人民币面值来讲解，给一组整数就得到1，2，5，10元面值的一个线性组合，比如一组整数4，0，1，2，得到4（1）+0（2）+1（5）+2（10），这个组合表示29元.其实在生活中，买东西需要付卖方29元，没有必要非要把钱凑够再给对方，完全可以给卖方30元，他找你1元即可，即给出的组合系数为-1，0，0，3.给定一组线性组合系数，就可以表示出相应的金额，比如3（1）+0（2）+2（5）+4（10）=53，那么53就可以由1，2，5，10元面值线性表示.

向量组线性相关性中有性质“有部分线性相关，则整体线性相关；整体无关，则任意部分均无关”.可以先利用定义进行证明，让学生理解性质内容，然后再给出恰当比喻，方便学生记忆.我们可以举生活中的例子，比如衣服上袖子有一个洞，就可以得到衣服是有洞的；衣服上无洞，则衣服的任意部分均无洞［5］.对于电气电子方向的学生，还可以利用电路开关的联通来理解这个性质.

5　增加实验教学

线性代数不仅要培养学生的抽象思维能力、科学运算能力，还要培养学生利用数学软件分析解决问题的能力.在线性代数方面最适宜的数学软件就是MATLAB.MATLAB能够进行矩阵计算、作图、数据拟合、数值积分微分计算、图像处理、仿真实验等，广泛地应用于数学分析、计算、自动化控制、数字信号处理、图像处理、数理统计、人工智能、通信工程和金融系统等领域.其中MATLAB的最强项目就是矩阵运算，计算效率远远高于C/C++，是工程计算线性方程组的计算软件.

结合MATLAB数学软件，让学生亲自动手计算行列式、矩阵、逆矩阵、解线性方程组、求方阵的特征值、特征向量等.不但帮助学生理解平时所学的知识，而且提高了学生的动手能力，为今后运用计算机进行数据处理及计算打下了良好的基础.MATLAB的融入使教师和学生从繁琐复杂的计算中解脱出来.在基本概念的教学基础上，教师更有精力去重点培养学生的分析问题、应用所学知识解决问题的能力.

实验教学中，教师可以有目的的创造一些实际问题，让学生自己动手解决.比如，加密技术是最常用的安全保密手段，即利用算法和密钥把重要的数据编码加密传送，到达目的地后再用相同或相反的手段解密.而密钥矩阵是一种新的编码方式，即用矩阵来编码.原理为:将要发送的明文信息数字化用矩阵P来表示，取可逆矩阵A为加密密钥，A左乘矩阵P得到密文Y=AP发出，收到方用密钥的逆矩阵左乘解密.如果小红的朋友给小红发来一封加密信［6］，它是一个三

图的邻接矩阵问题［7］，设V=｛v1，v2，…，vn｝是顶点集，称顶点间的有（vi，vj）为弧，以A表示弧的集合，则称G=（V，A）为图.一个图可以用一个矩阵来表示.称M=（aij）n×n为图G（V，A）的邻接矩阵，若

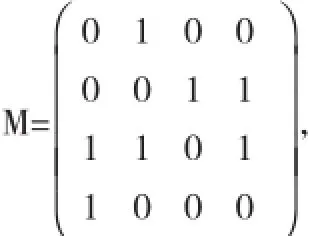
所以，从任一城市起飞可到达其余的城市（B4）ij.表示从vi到城市vj的航班数，如（B4）11=3.表示从vi起航返回v1有三条航线:v1v2v4v1，v1v2v3v1，v1v2v4v1.路长为3的两条（M3）11=2，路长为4的一条（M4）11=1.

《线性代数》在大学数学教学有着非常重要的基础地位，以上对如何提高《线性代数》教学效果给出五种措施.在教学过程中，教师应该深钻细研，精心设计组织教学结构和内容，巧妙地引入重要定义概念，采用问题式教学法启发学生思考，积极开展实验课程，提高学生利用数学软件分析问题、解决问题的能力.让学生在整个教学过程中，保持较高的学习兴趣，主动学习，高效掌握利用新知识.