二阶常微分方程组正周期解的存在性

袁志宏

（吕梁学院　数学系，山西　吕梁　033000）

二阶常微分方程组正周期解的存在性

袁志宏

（吕梁学院数学系，山西吕梁033000）

文章考虑二阶常微分方程组正周期解的存在性，用Green函数将求方程的解转化为求积分算子T的不动点，并且给出了不动点存在的充分条件，这一结论推广和改进了先前的结果.

二阶常微分方程；周期解

本文主要考虑下列二阶常微分方程组正周期解的存在性:

其中λ＞0，μ＞0为参数，连续，且f（·，u）:R→R+是t的T-周期函数.

我们所考虑的问题（1）中的非线性项与文［1］相同.文［1］利用Krasnosel'skill's不动点定理，研究了周期边值问题:

获得了关于正解的存在性和多重性的结果.在文献［2］中，Wang和An讨论了当λ＞-π2时，在对f做合适假设的前提下，得到二阶微分方程在Dirichlet边值问题条件下有一个解或两个解的结果.受此启发本文利用锥上的不动点定理获得了所研究问题的周期解的存在性和多重性的判别条件，主要利用Green函数将求方程的解转化为求积分算子T的不动点.

函数（u，φ）是方程（1）的正T-周期解，当且仅当

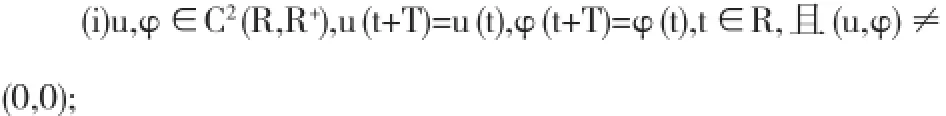
（ii）u，φ满足（1）式.

显然，问题（1）的正T—周期解等价于下列周期边值问题的正解:

于是，我们转化为求问题（2）的正解.

1　相关概念及引理、定理

首先给出下列定义，引理及定理，它们在后面主要结论的证明中起着非常重要的作用.

引理2.1Green函数G有下列性质:

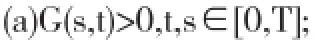
（b）存在C＞0，使得G（t，s）≤CG（s，s），t，s∈［0，T］；，其中C=eωΤ，

（c）存在σ＞0，使得G（t，s）≥σG（s，s）G（t，t），t，s∈［0，T］；对下列边值问题

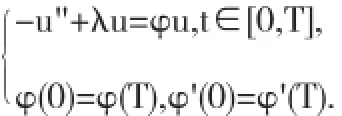
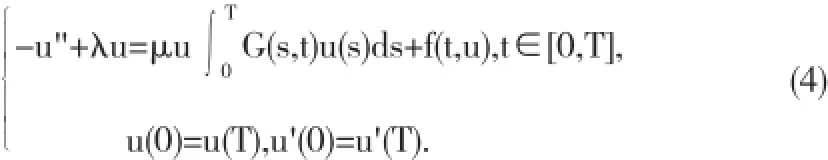
从而，问题（4）的解可以表示为

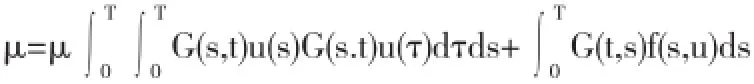
记［0，T］表示［0，T］上一切连续函数的全体，规定范数||u||=

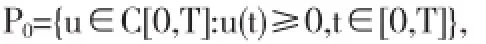
则P0是C［0，T］中的锥.

定义积分算子T:P0→P0为

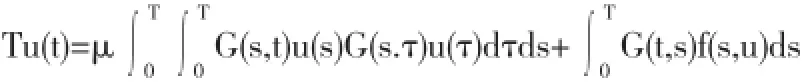
引理2.2算子T:P0→P0是全连续的.

证明设S是P0中的有界集，即存在a＞0，使得对任意的u∈S，有||u||≤a.再由引理2.1知，G是连续的，从而在闭区间［0，T］×［0，T］上有界，不妨设|G（t，s）|≤M，t，s∈［0，T］.于是

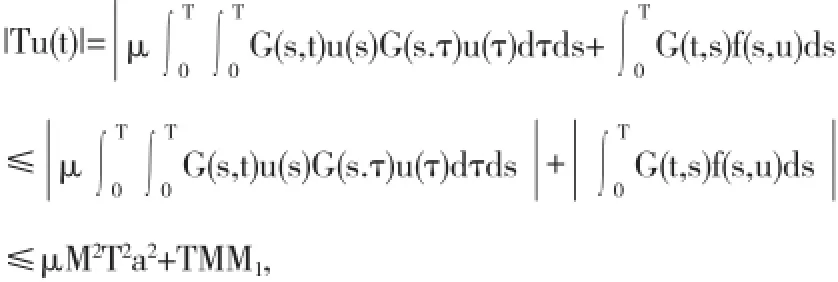
再证等度连续.由于G在区间［0，T］×［0，T］上一致连续，即对任给的ε＞0存在δ＞0，使得当t1，t2∈［0，T］，|t1-t2|＜δ时，对一切s∈［0，T］，恒有|G（t1，s）-G（t2，s）|＜ε.于是对于u∈S，有

从而T（s）中诸函数等度连续.

最后关于连续性，可容易证明.从而问题（4）的正周期解转化为求算子T的不动点.

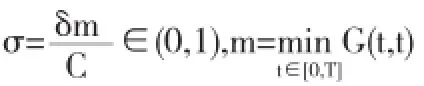
证明若u≥0是问题（4）的解，则

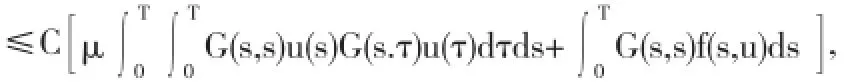
所以，

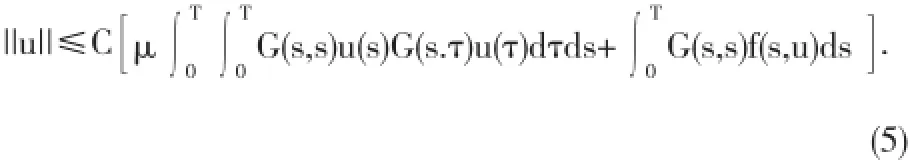
另一方面，结合（5）式，有

定义［3，定理4.4，p.314］E是Bannach空间，P⊂E是锥，设Ω1，Ω2是E中有界开集全连续.如果满足条件

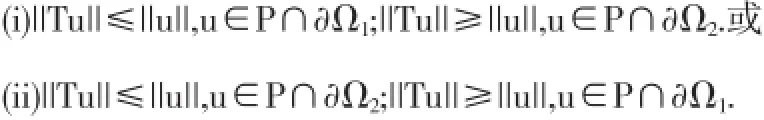
引理2.4Y（P）⊂P，且T:P→P是全连续的.

3　主要结论与证明

定理2.2假设下列条件成立:

证明由条件（A3）知，存在c1＞0，r∈（0，1），使得q（x）≤c1x，x∈［0，r］，且使下列式子成立:由引理2.1以及条件（A2），当u∈∂Br∩P时，可得

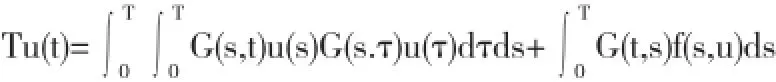
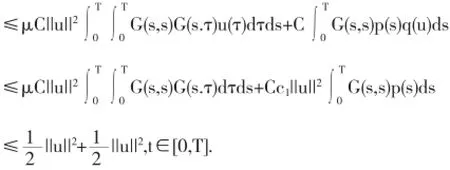
从而，

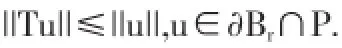
另一方面，由条件（A1）知，存在c2＞0，R1＞1使得

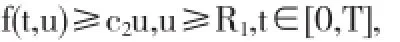
且满足

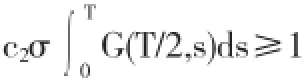
再结合条件（A2）和引理2.1，有

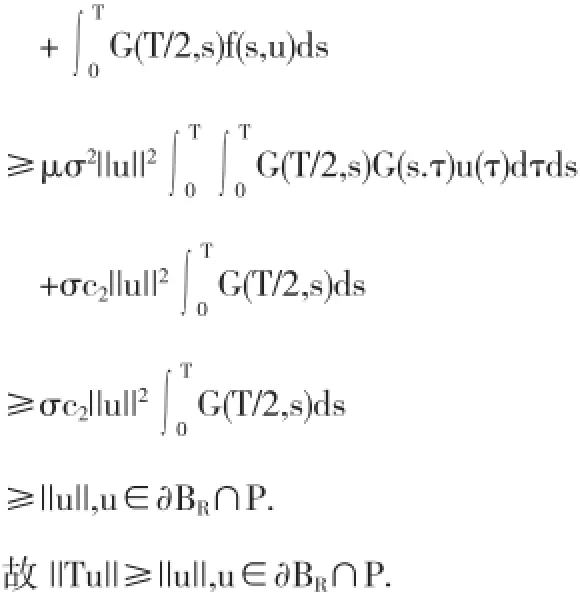
利用定理2.1，问题（2）至少有一个正解.

定理2.3假设条件（A1），（A2）成立，且满足条件:

有两个正解.

证明由条件（A2）和（A5），对任意的u∈∂BR∩P，有

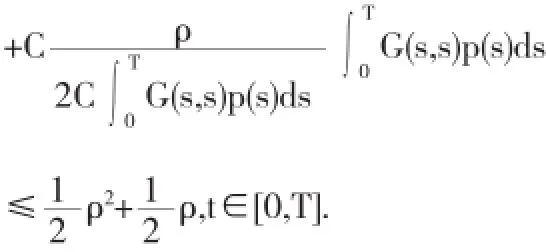
即||Tu||≥||u||，u∈∂BR∩P.

另一方面，由条件（A4）知，存在c3＞0，0＜r＜ρ使得

且满足

再结合条件（A4）和引理2.1，当u∈∂Br∩P时，有

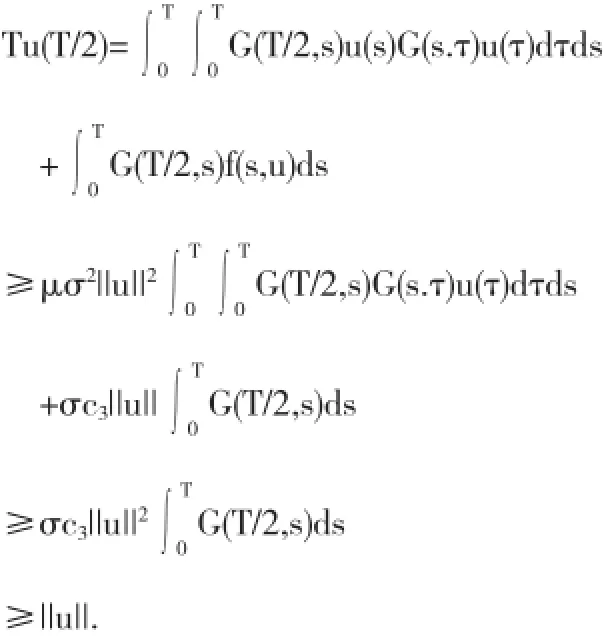
故||Tu||≥||u||，u∈∂BR∩P.由锥压缩拉伸定理可得，T在中至少有两个不动点，即问题（2）至少有两个解.

〔1〕F.M.Atici，G.S.Guseinov，Positive periodic solutions for nonlinear difference equations with periodic coefficients，J.Math.Anal.Appl.232（1999）166-182.

〔2〕F.Wang，Y.An，Positive solutions for a second-order differentialsystem，J.Math.Anal.Appl.373（2011）370-375.

〔3〕郭大钧.非线性泛函分析（第二版）.山东科学技术出版社，2001.

〔4〕Z.Zhang，J.Wang，On existence and multiplicity of positive solutions to periodic boundary value problems for singular nonlinear second order differential equations，J.Math.Anal.Appl.281（2003）99-107.

O177.91

A

1673-260X（2016）07-0010-03

2016-04-09